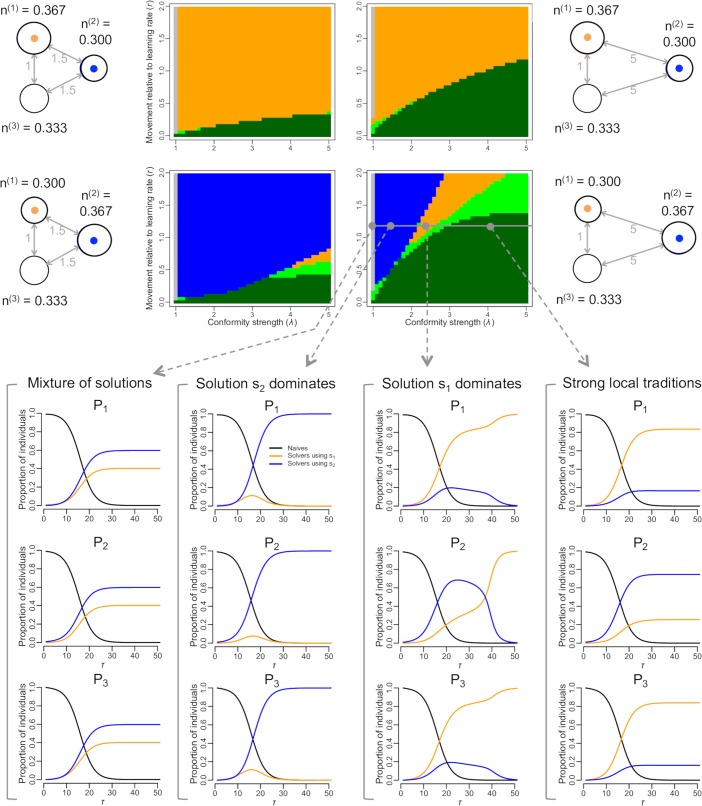
Fig 2. Spatial configuration of sub-populations has a complex effect on how conformity and movement lead to either the emergence of local traditions or the domination of a single solution.
This figure shows the model outputs in the three-sub-population case. At the start of every simulation, sub-population P1 contained innovators using solution s1 (1% of its population), sub-population P2 contained innovators using solution s2 (also 1% of its population), and sub-population P3 contained only naïve individuals. Each pixel in the phase diagrams corresponds to a simulation run with the corresponding parameter values, and the colour of the pixel indicates the emerging pattern after 150 days: grey = mixture of solutions in every sub-population, blue = solution s2 dominated the whole system, orange = solution s1 dominated the whole system, light green = weak local traditions, dark green = strong local traditions. The two columns of phase diagrams represent different spatial configurations; that is different distances between sub-population 2 and the other two sub-populations (whose distance separating them was set to 1), generating different movement rates between pairs of sub-population. The two rows of phase diagrams represent a different configuration of sub-population sizes, with n(k) indicating the proportion of the total population size in the system that occur in sub-population Pk. Four examples of the evolution of the proportion of naïve individuals (black curve) and proportion of solvers using solution s1 (orange curve) and solution s2 (blue curve) in each sub-population, are shown for fixed movement rate relative to the learning rate (r = 1.2), and spatial and sub-population sizes configuration, but with varying conformity strength. When no conformity bias was included (λ = 1), sub-population contained a mixture of solutions; when conformity was relatively weak (λ = 2), solution s2 ended up dominating in every sub-population; when conformity was intermediate (λ = 3), solution s1 ended up dominating in every sub-population; and when conformity was relatively strong (λ = 4), local traditions emerged.