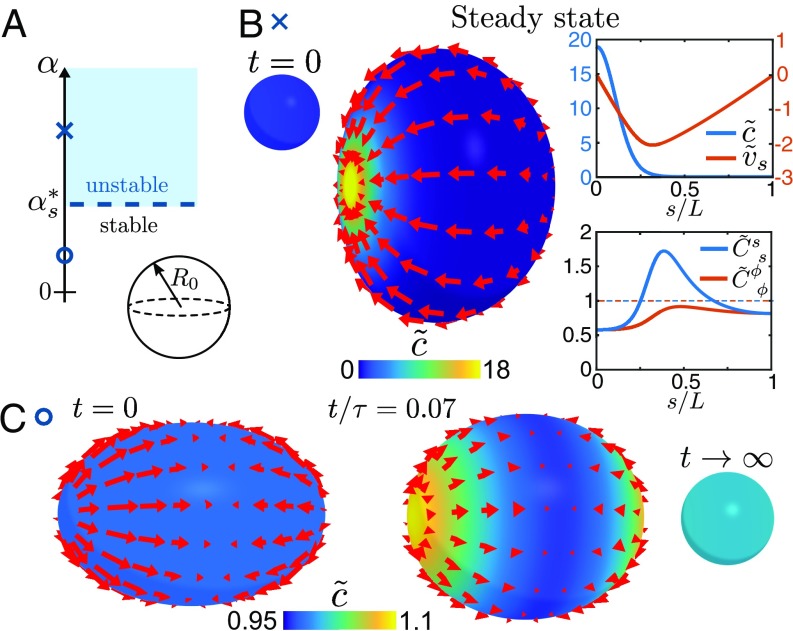
Fig. 2.

Shape dynamics of spherical surfaces with concentration-dependent active tension. (A) Schematic stability diagram of the system. The critical contractility ${\alpha }_s^{*}$ is independent of the bending rigidity $\kappa$. (B) Mechanochemically unstable surface with $\alpha >{\alpha }_s^{*}$ and $\kappa =0$. (Left) After a small concentration perturbation on a sphere ($t=0$, not to scale), a deformed steady-state shape emerges with a localized patch of stress regulator (Movie S1). Red arrows denote the in-plane flow field ${\mathbf{v}}_{\parallel }$. (Right) Profiles of the concentration $\tilde{c}=c/c_0$, in-plane flow ${\tilde{v}}_s=v_s\tau /R_0$ ($v_s={\mathbf{e}}_s\cdot \mathbf{v}$, $\tau ={\eta }_b/\gamma$), and principle curvatures ${\tilde{C}}_{\hspace{0.17em}s}^s=R_0{C}_{\hspace{0.17em}s}^s$, ${\tilde{C}}_{\hspace{0.17em}\varphi }^{\varphi }=R_0{C}_{\hspace{0.17em}\varphi }^{\varphi }$ of the steady-state surface. In the steady state, the diffusive outflux away from the contractile patch is balanced by an advective influx. The resulting tension across the surface is inhomogeneous, which leads to a deformed steady-state shape. (C) Relaxation dynamics of a mechanochemically stable surface with $\alpha <{\alpha }_s^{*}$ and $\kappa =0$, starting with a spheroidal shape with eccentricity 0.75 (Movie S2). Inhomogeneities in the initial mean curvature ($t=0$) lead to transient inhomogeneities in the concentration field ($t/\tau =0.07$) due to a deformation-induced local expansion and compression of the surface, before the stable steady state of a sphere is reached ($t\to \infty$, not to scale). Surface flows in B and C are shown in the reference frame where the pole velocities satisfy $\mathbf{v}\left(s=0\right)=-\mathbf{v}\left(s=L\right)$ (SI Appendix). The parameters used in these simulations are given in SI Appendix.