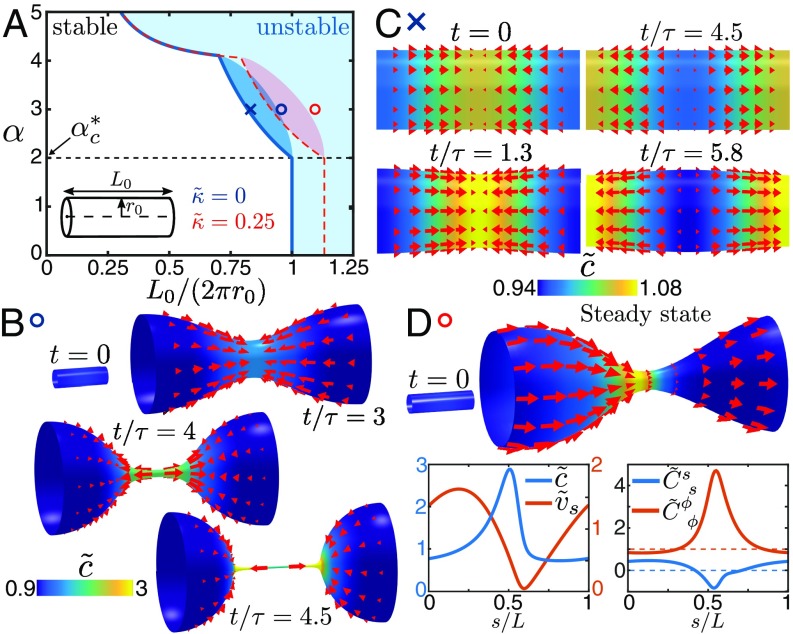
Fig. 3.

Shape dynamics of tubular active fluid surfaces with concentration-dependent active tension. (A) Representative stability diagram of the system. Stable and unstable regions are separated by the blue curve for $\kappa =0$ and the red dashed line for $\tilde{\kappa }=0.25$, where $\tilde{\kappa }=\kappa /\left(\gamma r_0^2\right)$. For $\kappa =0$ the dark blue-shaded region indicates parameter regimes where eigenvalues of the Jacobian are complex. The critical contractility ${\alpha }_c^{*}$ (Eq. 27) is described in the main text. (B) Concentration $\tilde{c}=c/c_0$ and in-plane flow ${\mathbf{v}}_{\parallel }$ (red arrows) during the spontaneous formation of a contractile ring (Movie S3) for parameters indicated with a blue circle in the stability diagram ($\tau ={\eta }_b/\gamma$, $t=0$ not to scale). This mechanism can constrict surfaces with aspect ratios below the Rayleigh threshold of $2\pi$. (C) Concentration and in-plane flow over one oscillation period for parameters indicated with a blue cross in the stability diagram (Movie S4). Oscillations result from the interplay between geometric stability of cylinder surfaces with $L_0/r_0<2\pi$ and the mechanochemical instability of the active fluid film. Surface flows in B and C are shown in the reference frame where ${\int }_0^L{v}_{s}ds=0$ (SI Appendix). (D) Steady state of directed surface flows relative to a constricted shape ($t=0$ not to scale). Shown are concentration (color code as in B), in-plane flow ${\tilde{v}}_s=v_s\tau /r_0$ ($v_s={\mathbf{e}}_s\cdot \mathbf{v}$), and principle curvatures ${\tilde{C}}_{\hspace{0.17em}s}^s=r_0{C}_{\hspace{0.17em}s}^s$, ${\tilde{C}}_{\hspace{0.17em}\varphi }^{\varphi }=r_0{C}_{\hspace{0.17em}\varphi }^{\varphi }$. The surface flow is shown in the reference frame where the constriction does not move (SI Appendix). In the reference frame where ${\int }_0^L{v}_{s}ds=0$, this steady state resembles peristaltic motion (Movie S5). The parameters used in these simulations are given in SI Appendix.