Modelling the dynamics of population viral load measures under HIV treatment as prevention

Abstract

In 2011 the Centers for Disease Control and Prevention (CDC) published guidelines for the use of population viral load (PVL), community viral load (CVL) and monitored viral load (MVL), defined as the average viral load (VL) of all HIV infected individuals in a population, of all diagnosed individuals, and of all individuals on antiretroviral treatment (ART), respectively. Since then, CVL has been used to assess the effectiveness of ART on HIV transmission and as a proxy for HIV incidence. The first objective of this study was to investigate how aggregate VL measures change with the HIV epidemic phase and the drivers behind these changes using a mathematical transmission model. Secondly, we aimed to give some insight into how well CVL correlates with HIV incidence during the course of the epidemic and roll out of ART. We developed a compartmental model for disease progression and HIV transmission with disease stages that differ in viral loads for epidemiological scenarios relevant to a concentrated epidemic in a population of men who have sex with men (MSM) in Western Europe (WE) and to a generalized epidemic in a heterosexual population in Sub-Saharan Africa (SSA). The model predicts that PVL and CVL change with the epidemic phase, while MVL stays constant. These dynamics are linked to the dynamics of infected subgroups (undiagnosed, diagnosed untreated and treated) in different disease stages (primary, chronic and AIDS). In particular, CVL decreases through all epidemic stages: before ART, since chronic population builds up faster than AIDS population and after ART, due to the build-up of treated population with low VL. The trends in CVL and incidence can be both opposing and coinciding depending on the epidemic phase. Before ART is scaled up to sufficiently high levels, incidence increases while CVL decreases. After this point, CVL is a useful indicator of changes in HIV incidence. The model predicts that during the ART scale-up HIV transmission is driven by undiagnosed and diagnosed untreated individuals, and that new infections decline due to the increase in the number of treated. Although CVL is not able to capture the contribution of undiagnosed population to HIV transmission, it declines due to the increase of people on ART too. In the scenarios described by our model, the present epidemic phase corresponds to declining trends in CVL and incidence.

1. Introduction

At the individual level, there has been accumulating evidence that demonstrates a direct relationship between HIV RNA concentrations in plasma (henceforth viral load or VL for short), infectivity, and HIV transmission (Attia, Egger, Mueller, Zwahlen, & Low, 2009; Bellan, Dushoff, Galvani, & Meyers, 2015; Lingappa et al., 2010), as well as the positive impact of antiretroviral treatment (ART) on reducing VL and, as a result, stopping HIV transmission (Cohen et al., 2011). Analogous to the individual case, aggregate population measurements of VL have been promoted as measures to assess the effectiveness of ART on HIV transmission and as a proxy for HIV incidence in this population (Herbeck & Tanser, 2016). The idea behind this hypothesis is that an aggregate VL is related to the magnitude of transmission in the population and that an ART-mediated decrease in the aggregate VL is associated with a reduction in HIV incidence.

The concept of population-level VL measures is compelling, since they make use of patients’ data collected routinely in HIV care to extract information on transmission in the population. Individual data are translated into a population-level measure by aggregating VL measurements via a procedure of averaging. Several aggregate measures have been proposed and investigated (Abu-Raddad et al., 2013; Castel et al., 2012; Das et al., 2010; Henard et al., 2012; Montaner et al., 2010; Rose et al., 2015), differing in what part of the HIV infected population is taken into account, and in how available VL measurements are averaged over that population.

In 2011 the Centers for Disease Control and Prevention (CDC) provided definitions and methods for calculating several population-level measures (Centers for Disease Control and Prevention, 2011) among which population viral load (PVL), community viral load (CVL) and monitored viral load (MVL). PVL was defined as the average VL of all HIV-infected persons in the population, both those unaware of their HIV status (undiagnosed) and those aware of their HIV status (diagnosed), whether or not linked to and retained in HIV care. CVL was defined as the average VL of all HIV-infected persons diagnosed with HIV in a given population. MVL was defined as the average VL of persons who have been diagnosed with HIV infection and are receiving HIV medical care and disease monitoring through VL testing. CDC has pointed out that PVL is more of a conceptual rather than a practical measure that cannot be directly calculated, while CVL was proposed as a surveillance tool (Centers for Disease Control and Prevention, 2011). The guidelines recommended using the mean as the summary analytic and to transform VL values to the logarithmic scale before computing the mean. We will refer to PVL, CVL and MVL measures computed in this way as the standard CDC measures.

Recently these and additional VL measures were compared in their performance in a cross-sectional study involving regional populations in India (Solomon et al., 2016) and in a retrospective longitudinal study using HIV monitoring data from the Netherlands (Bolijn et al., 2017). Importantly, while some aggregate measures seem to correlate with trends in HIV incidence or new diagnoses, it is unclear whether these statistical associations support their use for monitoring the impact of ART on HIV transmission.

Notably, Miller and colleagues (Miller, Powers, Smith, & Cohen, 2013) pointed out that biases due to potential unrepresentativeness of the diagnosed or treated population, hamper our ability to extrapolate from measures such as CVL to the entire HIV infected population. CVL based on averaging VL measurements over the diagnosed population does not take HIV prevalence into account, which is an important determinant of transmission risk (Miller et al., 2013). In particular, HIV incidence may be different for two populations with the same aggregate VL measures, but different HIV prevalence.

Mathematical modelling offers a tool to make the relationship between viral loads and transmission in a population transparent, because in a model population we have full information on who is infected in which stage of infection, and what are incidence and prevalence. In a model, incidence and prevalence are determined by the force of infection, i.e. the risk per time unit for a susceptible person of acquiring infection. This risk is given by the average infectiousness of the contact persons of a susceptible individual. So if infectiousness is directly related to viral load, the average viral load is proportional to the force of infection in a homogeneously mixing population. This holds if average viral load is calculated on the basis of all infected people (i.e. based on prevalence), but it may not hold if average viral load is calculated based only on those who are diagnosed. The proportion of the population, which is diagnosed, and the proportions of diagnosed and undiagnosed who are in the primary or chronic stage of infection, vary with epidemic phase. The aim of the work presented here is to give some insight using a model with disease stages that differ in viral loads into how well average viral loads based on diagnosed patients correlate with force of infection and therefore incidence during an HIV epidemic and roll out of treatment.

We used a compartmental model with stages of infection to study how PVL, CVL and MVL change during the course of a hypothetical HIV epidemic which goes through the exponential growth, diagnosis and ART scale up phases until it finally reaches the endemic equilibrium. We considered scenarios relevant for a concentrated epidemic in a population of men who have sex with men (MSM) in Western Europe (WE) and for a generalized epidemic in a heterosexual population in Sub-Saharan Africa (SSA) and identified the differences in the dynamics between the two scenarios. We studied how the VL measures are composed of viral loads from different infected subgroups (undiagnosed, diagnosed untreated and treated) and from infection stages (primary, chronic and AIDS). We investigated how contributions of the aforementioned subgroups change as the epidemic evolves. Most importantly, we were interested in the contribution to VL measures of infected persons who have not been diagnosed and, in particular, those who are in the primary stage of infection, because these groups potentially drive HIV transmission (Gray et al., 2018; Marks, Crepaz, & Janssen, 2006), while not being known to surveillance based on viral load measures. Finally, we studied whether trends in CVL predict trends in HIV incidence during different epidemic phases in the model population. We discussed implications for the usefulness of CVL as a proxy for HIV incidence depending on epidemic phase and roll out of treatment.

2. Methods

2.1. Study design

Our analysis was based on a compartmental mathematical model of sexual transmission of HIV, which was an extension of a model extensively described elsewhere (Granich, Gilks, Dye, De Cock, & Williams, 2009; Kretzschmar, van der Loeff, Birrell, De Angelis, & Coutinho, 2013). We considered two epidemiological settings: (i) heterosexual transmission in SSA countries as the scenario of a generalized HIV epidemic and (ii) homosexual transmission among MSM in WE countries as the scenario of a concentrated HIV epidemic in a high-risk group. The model describes HIV epidemic expansion, introduction and scale up of diagnosis and treatment in hypothetical SSA and WE populations. Our aim was not to fit the model to specific data, but to show qualitatively how standard VL measures change with time and phase of the epidemic. For this reason, we kept the model simple and did not include behavioral heterogeneity and other more complex aspects of human behavior. In particular, the model does not incorporate phenomena such as change in the number of partners upon HIV diagnosis, episodic risk and serosorting among others.

2.2. HIV model

Our deterministic model had compartments for the susceptible population and HIV-infected individuals who are unaware, diagnosed untreated, and treated. Each of these infected subgroups was stratified into four disease stages. For the non-treated groups these are primary infection; asymptomatic chronic stage; the last two stages together defined the symptomatic AIDS stage subdivided into infectious and noninfectious periods.

The transitions described HIV transmission with infectivity varying by stage, disease progression, diagnosis, ART uptake and dropping out from treatment. Susceptible individuals get infected with the force of infection $J=\lambda \left(P\right)\sum _{k=1}^4\left(h_k{I}_k+h_k{D}_k+\epsilon A_k\right)/N$, where $\lambda \left(P\right)$ is the transmission rate and $N$ is the total population size. $I_k$, $D_k$ and $A_k$ are the numbers of undiagnosed, diagnosed untreated and treated individuals in stage $k$ of infection, where $k=1$ (primary infection), 2 (chronic infection), 3 and 4 (AIDS). The force of infection takes into account that HIV infectivities vary between 4 disease stages for untreated individuals, $h_k$, $k=\mathrm{1,2,3,4}$ (see Supplementary Table 1). However, the model assumes that infectivities of diagnosed untreated and undiagnosed individuals are equal, i.e. we do not consider that, after being diagnosed with HIV, individuals might reduce their number of partners or take other measures to prevent HIV transmission. The infectivity for individuals on ART in any stage, $\epsilon$, is lower than infectivities for untreated population. Instead of modelling heterogeneity in sexual behavior explicitly, the observed steady state prevalence can be achieved in both scenarios if we allow transmission rate, $\lambda \left(P\right)$, to decrease with HIV prevalence, $P$ (Granich et al., 2009): $\lambda \left(P\right)={\lambda }_0\text{exp}\left(-\alpha P\right)$, where ${\lambda }_0$ is transmission rate at zero prevalence $P$. Parameter $\alpha$ describes how quickly the transmission rate decays for a given level of prevalence. Lower values of $\alpha$ correspond to epidemics with more pronounced peaks in HIV prevalence, while higher values of $\alpha$ produce epidemics where HIV prevalence increases and stays rather flat.

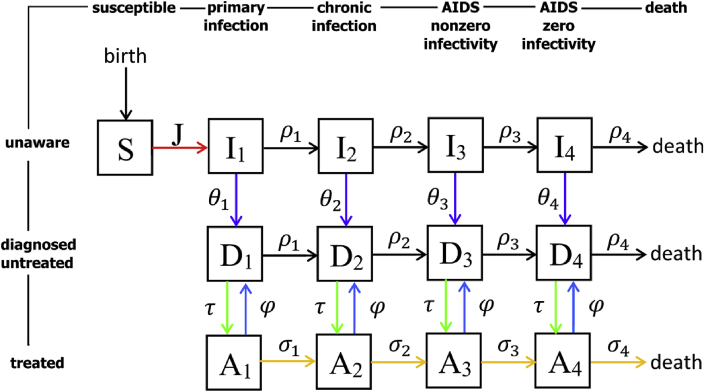
Demographic processes in the model were recruitment of susceptible population, AIDS related and background mortality. Dropping out from ART incorporated all reasons for stopping treatment including non-adherence, virological failure or others. The diagram summarizing the key assumptions of our model is shown in Fig. 1 while its detailed description is given in the appendix.

Fig. 1.

Sexual transmission model for HIV infection, diagnosis and treatment. Susceptible individuals ($S$) enter the population at constant rate and become infected ($I_1$) at rate $J$ (force of infection). Untreated individuals ($I_k$ and $D_k$) progress through disease stages at rates ${\rho }_k$$\left(k=\mathrm{1,2,3}\right)$ and die from AIDS at rate ${\rho }_4$. Infected individuals ($I_k$) get diagnosed ($D_k$) at rates ${\theta }_k$, $k=\mathrm{1,2,3,4}$. In any stage diagnosed individuals start treatment ($A_k$) at rate $\tau$. Treated individuals progress through disease stages at rates ${\sigma }_k$$\left(k=\mathrm{1,2,3}\right)$ and die from AIDS at rate ${\sigma }_4$. They can drop out of ART due to treatment failure or other reasons in any disease stage at rate $\varphi$. All individuals are subject to background mortality (not shown in the diagram).

2.3. Epidemiological scenarios

Generalized HIV epidemics in SSA and concentrated epidemics in WE differ in terms of circulating subtype, HIV testing rate, prevalence and incidence among other factors (Joint United Nations Programme on HIV/AIDS (UNAIDS), 2015). In this study our aim was to choose epidemiological parameters that plausibly described the two scenarios with only few key parameters differing between the two, which were the average time to diagnosis in chronic infection, annual dropout percentage and HIV prevalence level before the introduction of ART.

HIV testing and diagnosis became available already in the 1980's, while ART started only in the late 1990's. Both began to be used at low coverages, but were scaled up over the years, especially since WHO announced its “3 by 5” target in 2003, and more recently the “90-90-90” target (Joint United Nations Programme on HIV/AIDS (UNAIDS), 2014). Time to diagnosis differed by HIV stage. To model the scale-up over time, we assumed that in both scenarios the average time to diagnosis in chronic stage was 15 years during the first five years of the epidemic. This would progressively shorten to 2.6 years for WE (based on the 2011 estimate for MSM in the Netherlands (van Sighem et al., 2015)) and 7 years for SSA (World Health Organisation, 2015). For simplicity, we assumed that no individuals were diagnosed during primary infection. The average time to diagnosis during AIDS was one month (van Sighem et al., 2015). Supplementary Table 1 provides a summary of diagnosis rates in different stages used in the model scenarios.

Treatment uptake and dropout rates did not differ by HIV stage. We introduced ART from year 15 and assumed that ART uptake would start to scale up 5 years later to increase eventually to its maximum within 20 years. We used the maximal annual ART uptake of 50% for both scenarios and different baseline levels of annual dropout (5% for WE and 20% for SSA) to reflect consistently higher rates of dropout in SSA (Asiimwe, Kanyesigye, Bwana, Okello, & Muyindike, 2015). We considered two additional time points dubbed as ‘present’ and ‘endemic phase’ that corresponded to years 35 and 50 into the epidemic since its beginning. Due to the scale up of testing and treatment, ART coverage defined as the percentage of people on ART with respect to all HIV infected population would increase from its minimum value to 81% for WE and 54% for SSA. Supplementary Table 1 provides a summary of ART uptake and dropout percentages used in the model scenarios.

2.4. Population viral load measures

Following CDC (Centers for Disease Control and Prevention, 2011), we studied three standard population VL measures: population viral load (PVL), community viral load (CVL) and monitored viral load (MVL). PVL is the average VL of all HIV infected individuals in the population including both diagnosed and undiagnosed, independently whether or not they are on ART. CVL is the average VL of diagnosed individuals, independently whether or not they are on ART. Finally, MVL is the average VL of individuals on ART. The denominators used in the averaging of PVL, CVL and MVL were, respectively, all HIV infected population, all diagnosed population, and all population on ART. In addition to these three measures, CDC introduced in-care viral load measure that included persons who were in care but had no VL measurements available in the calculation of the population average. In this study, we assumed that all individuals had a VL measurement and therefore we did not study in-care viral load measure.

We also did not model variations in VLs of individuals in the same disease stage, i.e. all individuals in a given infected compartment in Fig. 1 had the same VL. We further assumed that HIV diagnosis does not influence a person's VL, that is why in our analysis VLs for undiagnosed and diagnosed populations who are not on ART were equal. The formulas used to compute PVL, CVL and MVL are given in Table 1.

Table 1.

Formulas for calculation of VL measures. Three measures were used in this study: population viral load (PVL), community viral load (CVL) and monitored viral load (MVL). Each of these measures is an average VL in a population in question. PVL is the VL averaged over the total infected population, CVL is the VL averaged over the diagnosed population, MVL is the VL averaged over the treated population. $I_k$, $D_k$ and $A_k$ are the numbers of undiagnosed, diagnosed untreated and treated individuals in stage $k$ of infection, where $k=1$ (primary infection), 2 (chronic infection), 3 and 4 (AIDS). $\sum _{k=1}^4(I_k+D_k+A_k)$ is the total infected population, $\sum _{k=1}^4(D_k+A_k)$ is the diagnosed population, and $\sum _{k=1}^4{A}_k$ is the population on ART. $V{L}_{I_k}$, $V{L}_{D_k}$ and $V{L}_{A_k}$ are VLs for the respective compartments, see Table 2 for their estimates.

VL measure	Description	Formula
Population viral load (PVL)	VL averaged over the total infected population	${\sum }_{k=1}^4(V{L}_{I_k}\times I_k+V{L}_{D_k}\times D_k+V{L}_{A_k}\times A_k)/{\sum }_{k=1}^4(I_k+D_k+A_k)$
Community viral load (CVL)	VL averaged over the diagnosed population	${\sum }_{k=1}^4(V{L}_{D_k}\times D_k+V{L}_{A_k}\times A_k)/{\sum }_{k=1}^4(D_k+A_k)$
Monitored viral load (MVL)	VL averaged over the treated population	${\sum }_{k=1}^{4}V{L}_{A_k}\times A_k/{\sum }_{k=1}^4{A}_k$

The VL assigned to each model compartment was the average VL in the respective disease stage reported in the literature (Table 2). VL values were always $lo{g}_{10}$ -transformed, and all VL measures were shown on the logarithmic scale. We considered VLs for untreated chronic (compartments $I_2$ and $D_2$) and AIDS stages (compartments $I_3,I_4$ and $D_3,D_4$) as reported in the study by Hollingsworth et al. (Hollingsworth, Anderson, & Fraser, 2008). During primary infection, regional differences in patients’ VL have been observed (Suthar et al., 2015). The average VL in SSA patients is about 1 $lo{g}_{10}$ copies/mL higher than in patients from the developed countries. For primary infection we took a $lo{g}_{10}$ VL of 5.5 for the WE scenario and of 6.5 for the SSA scenario (Suthar et al., 2015). The limit of HIV RNA detection, definitions of successful treatment and virological failure have been continuously changing during the past decades. Currently, in low-income and developed countries such as the NL successful treatment implies a VL of less than 1000 and 50 copies/mL, respectively. To reduce the number of model parameters and to simplify the model analyses, we assumed that effective treatment reduced VL to the detection limit of 100 copies/mL in both scenarios. The summary of VLs assigned to each model compartment is given in Table 2.

Table 2.

Viral loads assigned to each model compartment. PVL, CVL and MVL measures were computed using the estimates for the average VLs in undiagnosed $\left(I_k\right)$, diagnosed untreated $\left(D_k\right)$ and treated $\left(A_k\right)$ compartments for stage $k$ of infection, where $k=1$ (primary infection), 2 (chronic infection), 3 and 4 (AIDS). VL values were always $lo{g}_{10}$ -transformed. All VL measures were shown on the logarithmic scale.

VL notation	Compartment	VL (copies/mL)	$lo{g}_{10}$ VL	Source
$V{L}_{I_1}$, $V{L}_{D_1}$	$I_1$, $D_1$ (primary infection)	3162000 (SSA) 316000 (WE)	6.5 (SSA) 5.5 (WE)	(Suthar et al., 2015)
$V{L}_{I_2}$, $V{L}_{D_2}$	$I_2$, $D_2$ (chronic infection)	12500	4.1	(Hollingsworth et al., 2008)
$V{L}_{I_3}$, $V{L}_{D_3}$	$I_3$, $D_3$ (AIDS stage)	162000	5.2
$V{L}_{I_4}$, $V{L}_{D_4}$	$I_4$, $D_4$ (AIDS stage)	112600	5.1
$V{L}_{A_k}$, $k=\mathrm{1,2,3,4}$	$A_k$, $k=\mathrm{1,2,3,4}$ (treated compartments)	100	2	–

We computed the contributions of infected subgroups to PVL as $\sum _{k=1}^4(V{L}_{X_k}\times X_k)/\sum _{k=1}^4(I_k+D_k+A_k)$, where $X=I$ (for undiagnosed), $D$ (for diagnosed untreated) and $A$ (for treated). The relative contributions of each group (reported henceforth on the scale 0–100%) were computed as $\sum _{k=1}^4\left(V{L}_{X_k}\times X_k\right)/\sum _{k=1}^4\left(I_k+D_k+A_k\right)/PVL$, i.e. we divided the absolute contributions by PVL. The contributions of infected subgroups to CVL and the contributions of infection stages to PVL and CVL measures were computed following the same rationale.

3. Results

3.1. VL measures over time

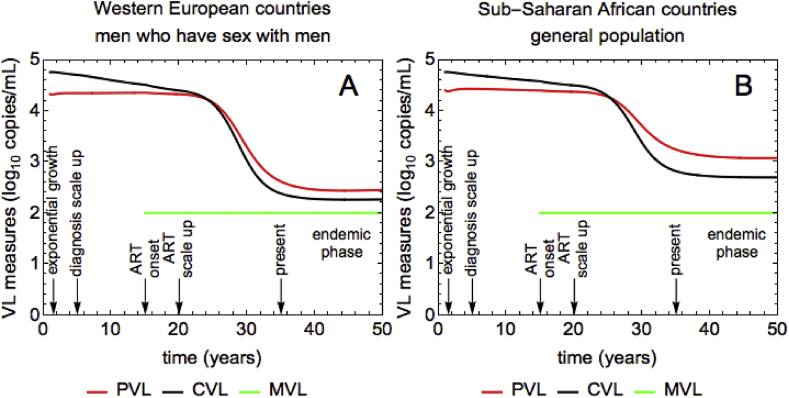
The temporal dynamics of PVL (red line), CVL (black line) and MVL (green line) measures are shown in Fig. 2. The panels A and B correspond to the WE and SSA scenarios, respectively. The measures are shown on $lo{g}_{10}$-scale. The arrows and text in each panel indicate different time points during the course of the HIV epidemic: exponential growth, diagnosis scale up, ART onset, ART scale up, present time and endemic phase. Since MVL (green line) is defined as the VL averaged over the treated population, it can only be measured after the onset of ART at year 15.

Fig. 2.

Time-dependent dynamics of VL measures and incidence for (A) WE and (B) SSA. PVL (red), CVL (black), MVL (green). The units of VL are HIV RNA copies per mL of plasma. The VL measures are shown on $lo{g}_{10}$-scale. The arrows and text indicate different time points during the course of the HIV epidemic: exponential growth, diagnosis scale up, ART onset, ART scale up, present time and endemic phase.

The MVL is constant over time. In both scenarios MVL is at the level of $lo{g}_{10}$ of 2 (or 100 copies/mL, see Table 2) immediately after the ART onset and remains constant after that. This is the consequence of our assumption that all treated individuals are effectively suppressed and have the same VL of 100 copies/mL independently of their disease stage. The dynamics of CVL (black line) and PVL (red line) are more complex, but qualitatively similar in both scenarios. The model predicts that PVL is nearly constant before the onset of ART following which it drops to a lower steady-state level. Unlike PVL, CVL decreases during the whole course of the epidemic, i.e. even before ART. At a given point in time, PVL and CVL are higher for SSA than for WE.

3.2. Contributions of infected subgroups and infection stages

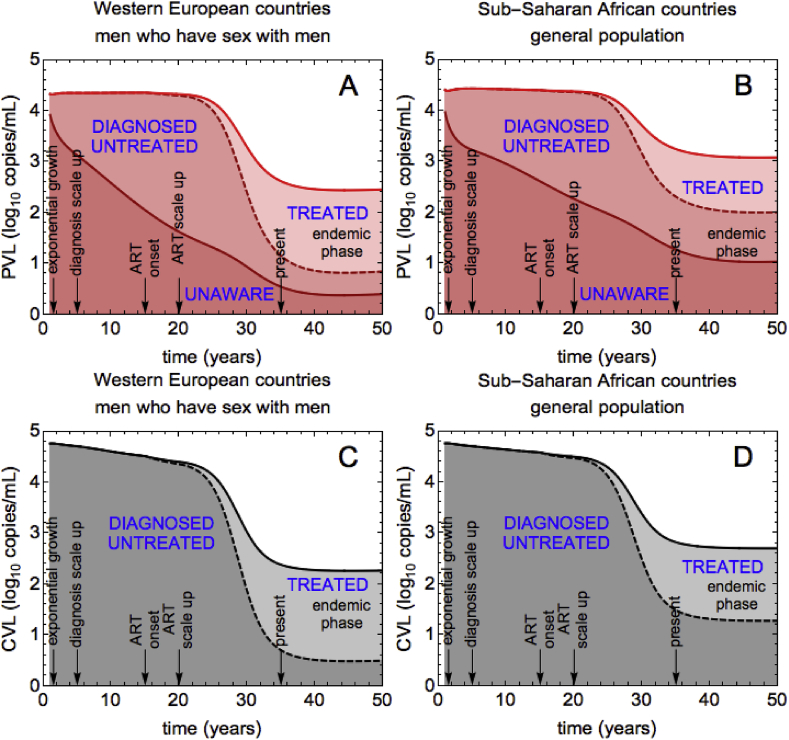
The differences in the temporal dynamics of the VL measures observed in Fig. 2 can be understood if we investigate how infected subgroups (unaware, diagnosed untreated, and treated) contribute to PVL, CVL and MVL during the epidemic course. The only individuals who contribute to MVL are those on ART, but since VL on ART is low, MVL stays low (and constant). In contrast, all three infected subgroups contribute to PVL (see Fig. 3, panel A for WE and B for SSA). Moreover, their contributions change as the epidemic evolves. In the exponential growth phase, most infected people are not aware of HIV infection, therefore the contribution of this subgroup to PVL is the largest (the relative contributions for WE: 72%, SSA: 73%). VL of these individuals is higher than VL of treated individuals which results in high PVL (Table 2). After the scale up of diagnosis, in both scenarios more people get diagnosed, thus the contribution of undiagnosed individuals decreases, and the contribution of diagnosed individuals increases. PVL stays, however, nearly constant until the introduction of ART. This behavior of PVL is the consequence of our assumption that VL of individuals does not change upon HIV diagnosis (Table 2). Finally, after the scale up of ART treated population increases and thus its contribution to PVL. However, since this subgroup has a low VL, the ART scale up leads to a decrease in PVL. At the endemic equilibrium the largest contribution to PVL for WE is made by the treated population (66%), with unaware and diagnosed untreated populations contributing almost equally (16% and 18%). For SSA, the steady state contributions are different. Unlike for WE, the contributions of all three groups to PVL are nearly equal. This is due to the fact that, in the SSA scenario, longer times from infection to diagnosis and higher rates of dropping out from ART lead to much larger numbers of undiagnosed individuals and lower numbers of treated individuals than in the WE scenario. For SSA, the contribution of undiagnosed to PVL in the endemic equilibrium is 34% as compared to 16% for WE.

Fig. 3.

Contributions of infected subgroups to PVL and CVL for WE and SSA. (A), (B) The contribution of the unaware/diagnosed untreated/treated population to PVL is the dark red/intermediate red/light red shaded region. (C), (D) The contribution of the diagnosed untreated/treated population to CVL is the dark gray/light gray shaded region. In the main text we report on the relative contributions of infected subgroups (range 0–100%) at a given time, which we obtain by dividing the absolute contributions shown in the figure by PVL (or, respectively, CVL).

The contributions of infected subgroups to CVL are shown in Fig. 3 C for WE and D for SSA. Only two subgroups are used to compute CVL, namely diagnosed untreated and treated individuals. As expected, the contribution of diagnosed untreated is 100% up until the introduction of ART, after which it starts to decrease. In the same way as for PVL, the drop in CVL after the onset of ART occurs because treated population increases but its VL is low. This picture, however, is not sufficient to explain why CVL decreases even before ART when diagnosed untreated population contributes 100%. We therefore studied how the contributions of infection stages to CVL change during the course of the epidemic.

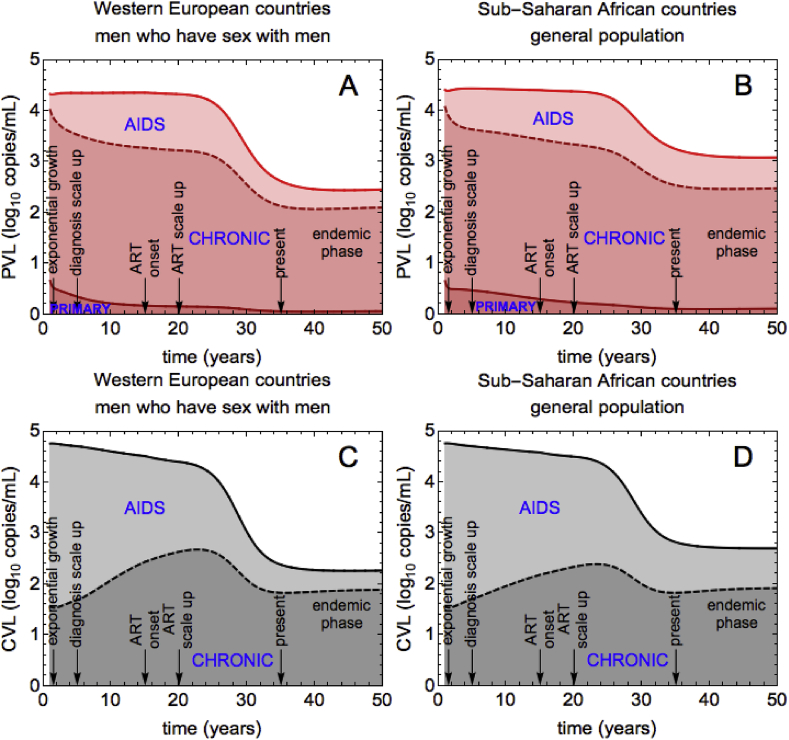
Our model assumes that individuals with primary infection are not diagnosed, therefore only chronic and AIDS stages contribute to CVL (Fig. 4 C for WE and D for SSA). In the exponential growth phase, AIDS characterized by high VLs made the dominant contribution to CVL (WE and SSA: 64%). From this moment and until the beginning of ART, the contribution of AIDS patients decreases with time and the contribution of chronic infection increases, with the overall CVL decreasing. This is counterintuitive because without treatment we would expect the higher numbers of people diagnosed in chronic stage to lead to higher numbers of people diagnosed with AIDS. The CVL should therefore increase instead of decreasing. However, it is important to notice not only that the numbers of individuals in chronic and AIDS stages increase, but the rate with which this happens. In the model, the chronically infected diagnosed population grows faster than the AIDS diagnosed population, which leads to a decrease in CVL, even in the absence of ART (see Supplementary Fig. 3). After ART, most people are chronically infected and, thus, they contribute more than people with AIDS (WE: 83%, SSA: 71%), who are fewer.

Fig. 4.

Contributions of infection stages to PVL and CVL for WE and SSA. (A), (B) The contribution of primary infection/chronic infection/AIDS to PVL is the dark red/intermediate red/light red shaded region. (C), (D) The contribution of chronic infection/AIDS to CVL is the dark gray/light gray shaded region. In the main text we report on the relative contributions of infection stages, which we obtain by dividing the absolute contributions shown in the figure by PVL (or, respectively, CVL).

Lastly, we would like to point out that the contribution of individuals with primary infection can only be captured for PVL measure (Fig. 4 A for WE and B for SSA). In the very beginning we expect to have many people in the primary stage. As the epidemic evolves, these people progress further through HIV stages, so the contribution of primary infection decreases and becomes minimal in the steady state (WE: 2.5%, SSA: 3.5%). Relative contributions to PVL of chronic and AIDS stages change very little during the epidemic's course, with most of PVL being due to chronic infection.

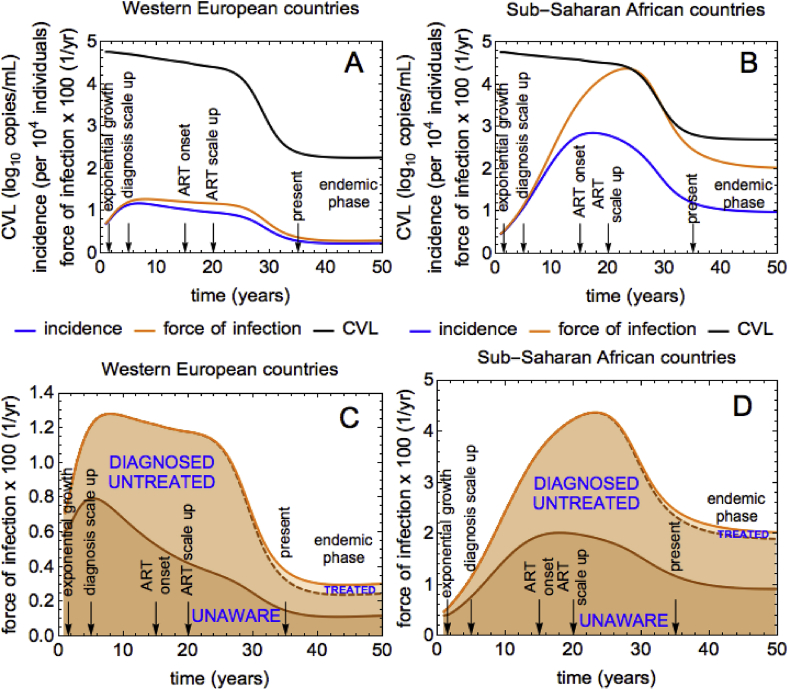
3.3. Association between CVL and transmission

Our model predicts that HIV incidence (blue line) peaks during the first/second decade after the beginning of the epidemic for the WE/SSA scenario, after which it declines to a steady state (see Fig. 5 A/B, respectively). We saw in Fig. 2 that after the ART scale up which starts at year 20, both PVL and CVL declined too (unlike MVL which stays constant). This suggests that both measures could potentially be used to monitor trends in HIV incidence. Since PVL includes VLs of undiagnosed individuals when computing the average this measure can be used in modelling work but it is not useful in surveillance. On the other hand, CVL can be easily estimated in epidemiological practice using VL data of all diagnosed individuals in a given location/community.

Fig. 5.

Association between CVL and HIV transmission for WE and SSA. (A), (B) Incidence (blue), force of infection per year (orange) and CVL measured in HIV RNA copies/mL (black) for WE and SSA. CVL is shown on $lo{g}_{10}$-scale. HIV incidence is shown per 10000 individuals. The force of infection is multiplied by 100 so that it can be shown in the same plot with CVL and incidence. (C), (D) Contributions to the force of infection by unaware, diagnosed untreated and treated individuals. The sum of the three contributions is the total force of infection.

The behavior of HIV incidence (blue line, Fig. 5 A and B) in our model is qualitatively similar to the behavior of HIV transmission rate or the force of infection (orange line, Fig. 5 A and B). This happens because, by definition, HIV incidence is the force of infection multiplied by the number of susceptible individuals. To understand why incidence and CVL (black line, Fig. 5 A and B) have the same trend when ART is scaled up, we examined how the rates of transmission from infected subgroups change with time. Fig. 5 B and C show the contributions to the force of infection by undiagnosed, diagnosed untreated and treated individuals. The total force of infection is the sum of the three contributions. The scale up of ART drastically reduces HIV transmission. New infections are driven by undiagnosed and diagnosed untreated individuals, with a tiny contribution attributed to treated individuals due to their very low infectivity. As discussed, the decline in CVL after the treatment scale up is expected too. The same build-up of treated population leads to them contributing more to CVL but, since their VL is low (as compared to untreated individuals), CVL declines. We therefore see that transmission processes from different infection groups and CVL dynamics are closely related. However, unlike the force of infection, CVL does not capture the transmission by people who are unaware of HIV infection. Importantly, the link between decreasing CVL and incidence under ART could not be explained by looking at the proportions of diagnosed untreated and treated individuals alone. Unlike CVL and incidence, after the start of ART at year 15 these proportions demonstrate the opposite pattern, namely they keep on increasing until years 24 and 36 into the epidemic, respectively (Supplementary Fig. 3).

4. Discussion and conclusions

We examined the dynamics of standard VL measures through the modelling of a generalized HIV epidemic in a representative population in SSA and a concentrated HIV epidemic in a representative population of MSM in WE. In this study we used mathematical modelling instead of analysis of within-patient VL data only. This kind of empirical model was crucial for exploring the dynamics of VL measures during the whole course of an HIV epidemic for which no data is usually available and for understanding what drives these dynamics.

We found that PVL and CVL change with the epidemic phase, and MVL stays constant. The temporal dynamics of PVL and CVL depends on the contributions of different infected subgroups and infection stages to these measures. The model predicts that in both scenarios CVL decreases during the course of the epidemic. Before the introduction of ART, CVL declines because the chronically infected population grows much faster than the AIDS population. After ART is introduced, CVL declines because of the increasing treated population who has very low VL.

There has been considerable disagreement on whether CVL can be used to assess the impact of ART on transmission (Miller et al., 2013). Das et al. (Das et al., 2010) found that longitudinal reductions in CVL were associated with reductions in new HIV diagnoses and incidence, while Castel et al. (Castel et al., 2012) did not. In another study, Herbeck and colleagues (Herbeck, Mittler, Gottlieb, & Mullins, 2014) concluded that CVL was not a strong predictor of HIV incidence too, but their model did not include ART which is the essential factor that affects the dynamics of CVL. In this work, we showed that trends in the behavior of HIV incidence and CVL can be different depending on the course of a particular epidemic, the timing of different interventions, and other characteristics such as time to diagnosis, ART uptake, and dropout rates. Since the beginning of the epidemic up until ART is scaled up to higher levels, HIV incidence in the model has a trend opposite to that of CVL. In this time period, CVL decreases while incidence increases. After incidence has reached its maximum, both quantities have the same declining trend. By analyzing the force of infection, we concluded that new infections decline due to the increase in the number of treated, and that HIV transmission is driven by undiagnosed and diagnosed untreated individuals. Although CVL declines due to the increase of people on ART, this metric is not able to capture the contribution of undiagnosed population to HIV transmission. The two quantities therefore have the same trend, but there is no simple relationship between them.

The contribution of undiagnosed individuals and of primary infection can only be captured by the PVL measure. In the modelling scenarios, we observed that the contribution of primary infection to PVL decreases during ART scale up and is minimal at the endemic equilibrium (WE: 2.5%, SSA: 3.5%). We found substantial differences between the two scenarios concerning the contribution of undiagnosed to PVL with an at least twice higher proportion for SSA (34%) than for WE (16%). This finding is a reflection of a much longer time to diagnosis during chronic infection and higher dropout from ART in SSA than in WE. Undiagnosed individuals may comprise up to 25% of the HIV infected population in the Western countries (estimates for the USA (Hall, Holtgrave, & Maulsby, 2012; Marks et al., 2006)) and be responsible for more than half of all HIV transmissions. We expect that if undiagnosed individuals had riskier behavior or if higher risk behavior were correlated with higher VLs their contribution to PVL could be larger than in our analysis.

Our model was too simple for addressing some of the questions relevant for MSM transmission in WE. First of all, it did not include any sort of behavioral heterogeneity important for HIV transmission in this population. The possible impact of behavioral heterogeneity on the contribution of undiagnosed individuals to VL measures can be studied using an extended model where population is stratified by the rate of acquisition of sexual partners (Rozhnova, van der Loeff, Heijne, & Kretzschmar, 2016). Without explicitly accounting for behavioral heterogeneity our model was not suitable to investigate the impact on VL measures of changes in risk behavior over time. We also assumed that HIV diagnosis did not impact the model transmission parameters. Unrealistically assuming that risk behavior does not change over time in individuals has been shown to dramatically decrease the fraction of transmissions from primary infection (Henry & Koopman, 2015). We expect that adding changes in risk behavior to the model might lead to a larger contribution of primary infection to PVL in the WE scenario.

Another drawback of our model is that it did not account for heterogeneity in VL measurements between individuals in different infection subgroups. Instead, we assumed that all individuals during a given HIV stage had the same VL value extracted from the literature. This greatly simplified the analysis of the model but could have a large impact on our conclusions. Other important assumptions were that VL of individuals did not change upon diagnosis and the choice of VL of individuals on ART. Since the start of ART, the guidelines for successful treatment have been different for WE and SSA and have been constantly updated. To reduce the number of parameters and to simplify the model analyses we used just one VL value for both scenarios during the time span of 50 years. The model therefore silently assumed that all treated patients were virally suppressed to the detection limit of 100 copies/mL as their VL while, in reality, some patients who are in care may have an undetectable VL or have no current VL measurement if the test was not taken. An extended model without these assumptions can be developed in the follow-up work. Finally, VL value assigned to a given disease stage was not directly linked to infectivity in that stage (Blaser et al., 2014). We extracted most estimates for these parameters from the same source (Hollingsworth et al., 2008) but we did not include an explicit relationship between the two in the model. For this reason, we could not explicitly relate the force of infection and VLs in different infection stages.

To summarize, we examined how standard VL measures change as the HIV epidemics evolve. The model predicted that CVL decreases through all epidemic phases and that, after ART is scaled up to higher levels, CVL and incidence have the same decreasing trend. In the scenarios described by out model, CVL would therefore be a useful indicator of changes in HIV incidence. In future work, more complex models have to be explored in order to corroborate our results and to test other VL measures which could potentially be useful for HIV surveillance.

Declaration of interest

There are no competing interests.

Authors’ contributions

G. R. and M. K. conceived and designed the study. M. A. worked on developing the model. G. R. developed the final model and performed all analyses. G. R. wrote the manuscript. M. A. and M. K. commented on the manuscript and approved its final version.

Handling editor: James Koopman

Abbreviations

ART

antiretroviral treatment

MSM

men who have sex with men

SSA

sub-Saharan Africa

WE

Western Europe

VL

viral load

PVL

population viral load

CVL

community viral load

MVL

monitored viral load

Appendix A. Supplementary data

The following is the Supplementary data to this article: