FIG. 1. Analyzing MacArthur Consumer’s Resource Model for large, diverse ecosystems.
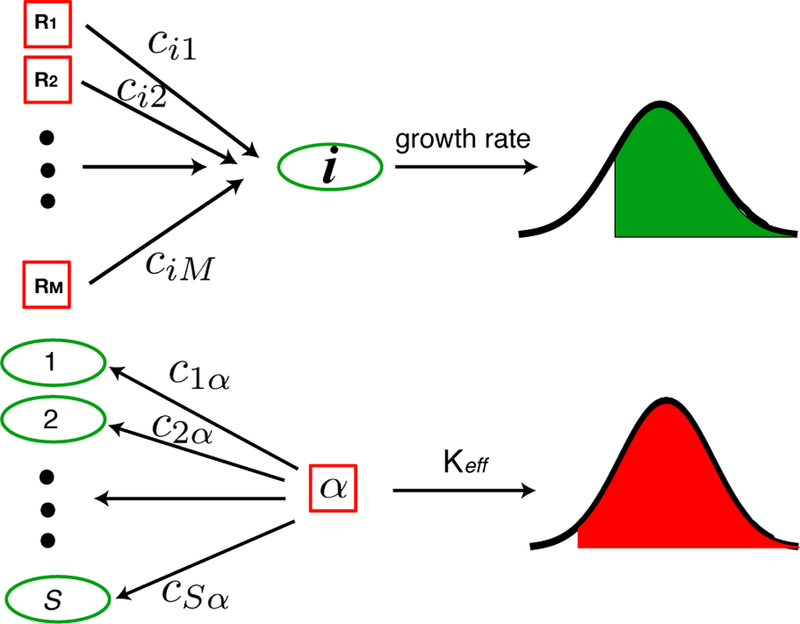
(Top) The growth rate for a species i is a sum of terms resulting from consuming M ≫ 1 resources. For this reason, from the central limit theorem, it can be well modeled by a (truncated) normally distributed variable. (Bottom) Each resource α is consumed by S ≫ 1 consumers. From the central limit theorem, the effective carrying capacity of the resource (i.e. the resource abundance at steady-state) can also be modeled using a (truncated) normal distribution. The truncation is due to the fact that neither species nor resource abundances can become negative. To derive our analytic cavity equations, we require selfconsistency for the means and variance of these distributions.
