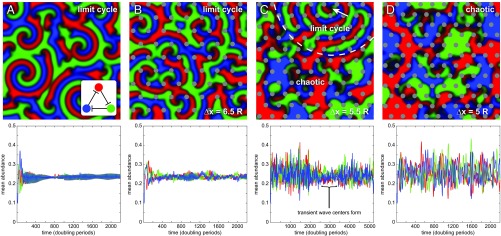
Fig. 3.

Structurally anisotropic environments disrupt spatial patterns and cyclic dynamics in intransitively competing three-species communities. (Top) Snapshots of spatial distributions from representative simulations, with (Bottom) corresponding abundance dynamics. (A) Following a brief “grow-in” period, isotropic conditions result in spiral waves and cyclic abundance dynamics with corresponding stable coexistence. The Inset illustrates the intransitive competitive network topology, with flat-headed arrows indicating predation. (B) Introducing pillars spaced far apart compared with the natural length scale of the system slightly perturbs wave center formation and dynamics, but the system still robustly exhibits spiral waves and stable coexistence. (C) Moving pillars closer disrupts cyclic pattern formation, leading to irregular spatial distributions and large fluctuations in species abundance. However, in this example, transient wave centers form (white arrow) and produce locally stable cyclic dynamics, indicated by the dashed boundary in Top. Note the longer time scale on this plot. (D) More densely packed pillars hinder transition to a limit cycle, resulting in sustained large fluctuations in abundance and irregular species distributions that exhibit extreme sensitivity to perturbations and corresponding chaotic dynamics. See SI Appendix for demonstration of positive Lyapunov exponents. Movies S7–S10 correspond to A through D, respectively. Simulation parameters are L/(1.29 λ) = 150, P = 0.1, A_min = 0, and, for simulations including pillars, R/(1.29 λ) = 3 and Δx as indicated.