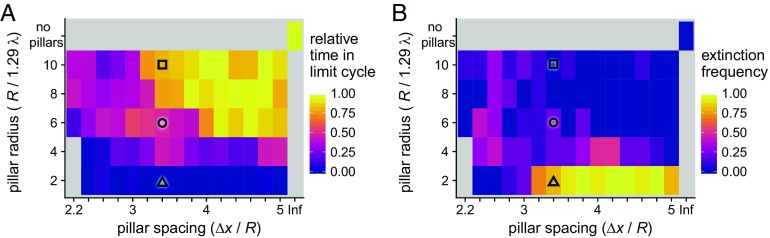
Fig. 5.

Severity of chaotic disruptions depend on structural characteristics of the environment. Over 1,000 doubling times, A shows the fraction of time the system displayed cyclic dynamics, and B shows extinction frequency, both as functions of the size and spacing of the pillar array. Ten simulations were performed for each grid point. For each simulation, the amount of time spent in a limit cycle was normalized by the average time that isotropic simulations were classified as cyclic; this adjusts for systematically acyclic periods such as the grow-in phase. Three primary dynamic regimes were identified: (i) stable cycles, with larger and widely spaced pillars (square symbol); (ii) a transitory region at intermediate pillar size and spacing, where communities tend to either relax into a limit cycle or collapse (circle); and, (iii) when pillars are small and densely packed, unstable chaos with rapid community collapse (triangle). Simulation parameters are L/(1.29 λ) = 100, P = 0.1, and A_min = 0.01, with pillar size and spacing as indicated in the figure. The simulations at R/(1.29 λ) = 2 and 4 with Δx/R = 2.2 were omitted because the pillar spacing did not allow for accurate simulation of diffusion. Black symbols correspond to simulation conditions whose extinction time distributions were analyzed in Fig. 6.