Fig. 1.

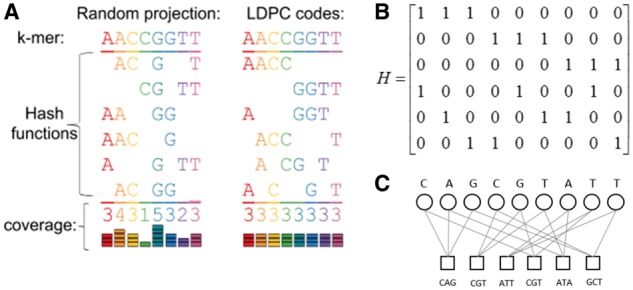
Low-density hashing with even coverage. (a) Random projections onto subspaces (left) cover all positions evenly only in expectation, and for small numbers of hash functions, will give uneven coverage. Using Gallager-inspired LDPC codes allows us to guarantee even coverage of all positions in the $k$-mer (right) with a small number of hash functions. (b) Intuitively, one can think of a ($k$, $t$)-hash function as a 0/1 vector of length $k$ with $t$ 1’s specifying the locations in the $k$-mer that are selected. Given any ($k$, $t$)-hash function h (e.g. the vector with $t$ 1’s followed by $k$ -$t$ 0’s), one can uniformly randomly construct another ($k$, $t$)-hash function by permuting the entries of $h$. The key to the Opal’s Gallager-inspired LSH design is that instead of starting with a single hash function and permuting it repeatedly, we start with a hash function matrix$H$ which is a LDPC matrix. $H$ is designed such that in the first row $h_1$, the first $t$ entries are 1, in the second row $h_2$, the second $t$ entries are 1 and so on, until each column of $H$ has exactly one 1. Permuting the columns of $H$ repeatedly generates random LSH functions that together cover all positions evenly, ensuring that we do not waste coding capacity on any particular position in the $k$-mer. Additionally, for very long $k$-mers, we can construct the Gallager LSH functions in a hierarchical way to further capture compositional dependencies from both local and global contexts (see Section 2). (c) The rows of $H$ are then used as hash functions