POTENTIAL STRAIN-DEPENDENT MECHANISMS DEFINING MATRIX ALIGNMENT IN HEALING TENDONS

Abstract

Tendon mechanical function after injury and healing is largely determined by its underlying collagen structure, which in turn is dependent on the degree of mechanical loading experienced during healing. Experimental studies have shown seemingly conflicting outcomes: although collagen content steadily increases with increasing loads, collagen alignment peaks at an intermediate load. Herein, we explored potential collagen remodeling mechanisms that could give rise to this structural divergence in response to strain. We adapted an established agent-based model of collagen remodeling in order to simulate various strain-dependent cell and collagen interactions that govern long-term collagen content and fiber alignment. Our simulation results show two collagen remodeling mechanisms that give rise to divergent collagen content and alignment in healing tendons: (1) strain-induced collagen fiber damage in concert with increased rates of deposition at higher strains, or (2) strain-dependent rates of enzymatic degradation. These model predictions identify critical future experiments needed to isolate each mechanism’s specific contribution to the structure of healing tendons.

1. INTRODUCTION

Tendon injury is a prevalent source of health care expenditures and lost productivity, with rotator cuff tears alone affecting 4% of Americans <40 years old and 50% of Americans >60 years old (Sher et al. 1995). Even after surgical repair and long periods of healing, tendons are often left with diminished mechanical properties such as stiffness and ultimate tensile load, and these reduced properties coincide with high refailure rates and/or reduced function (Thomopoulos et al. 2003; Valencia Mora et al. 2015). Collagen content and alignment are critical determinants of tendon mechanics, so not surprisingly, reductions in mechanical stiffness and ultimate load of tendons post-injury are associated with reduced matrix alignment (Thomopoulos et al. 2003).

It is now clear that the degree of loading experienced by a tendon during healing affects both collagen content and alignment. Interestingly, increasing loads progressively increase tendon collagen content, while alignment and mechanical properties (e.g., stiffness and ultimate tensile load) peak with an intermediate level of loading during healing (Thomopoulos et al. 2003; Galatz et al. 2009). One common explanation for this divergence – increased collagen content but decreased alignment – at higher levels of loading is that it arises from strain-induced “micro-damage” to collagen (Kamps et al. 1994; Thomopoulos et al. 2003; Gimbel et al. 2007). This idea suggests that fibers parallel to the direction of loading would experience the greatest degree of strain and be most likely to rupture, while fibers oriented away from the loading axis would be more likely to remain intact, thereby reducing the overall degree of collagen alignment.

As an alternative explanation for the divergence of fiber content and alignment with increasing load, experiments have also shown that enzymatic degradation of collagen by matrix metalloproteinases (MMPs) can depend on fiber strain such that intermediate strains protect those fibers from degradation, while both higher and lower strains lead to higher degradation rates (Huang and Yannas 1977; Ghazanfari et al. 2016). In the current study, we used a computational agent-based model of cell and collagen remodeling to explore the effects of both strain-dependent damage and strain-dependent degradation on tendon matrix content and alignment during healing.

2. METHODS

2.1. Simulation Overview

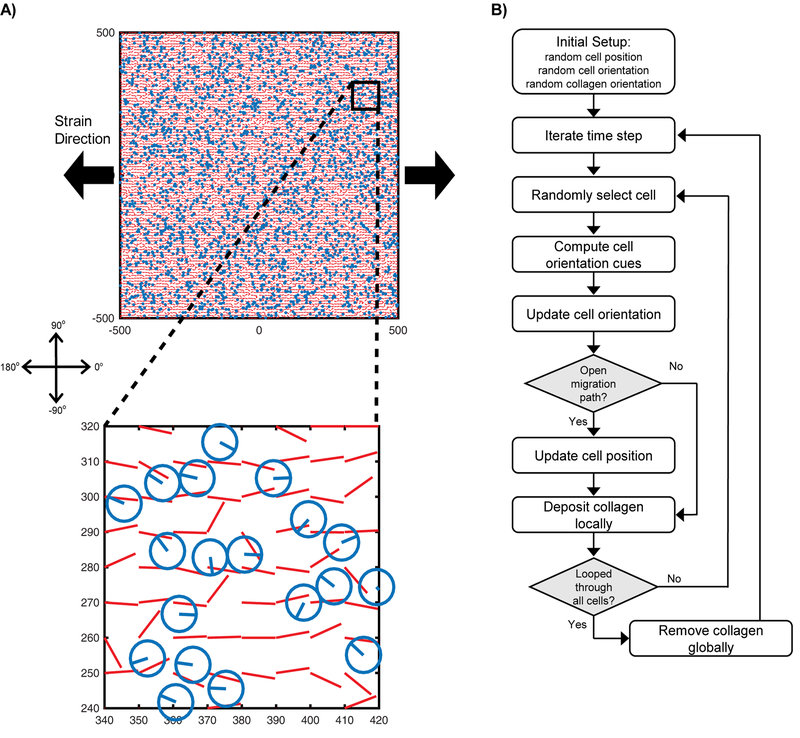
For this study, we adapted a previously published agent-based model of scar formation after myocardial infarction that simulated fibroblast turnover, migration, orientation, collagen deposition, degradation, and reorientation all in response to mechanical, structural, and chemical cues (Rouillard and Holmes 2012). Herein, we simulated a 1mm × 1mm region of healing tendon subdivided into a grid of 10μm × 10μm collagen-containing elements and populated with 3000 randomly-positioned fibroblasts (Figure 1). Each element contained a distribution of fibers oriented in 5° bins from −90° to 90°, where 0° corresponded to the direction of global tissue extension. Each fibroblast was simulated as a disc of 5μm radius with an orientation angle ranging from −180° to 180°.

Fig. 1. Agent-based model overview.

(A) 3000 fibroblasts were randomly dispersed across a 1mm × 1mm array of collagen fibers. Fibroblasts were each represented as a disc of 5 μm radius and orientation between −180° and 180°, with 0° corresponding to the direction of global tissue extension. Collagen fibers were represented as a grid of 10μm × 10μm elements, each containing a distribution of fibers oriented in 5° bins from −90° to 90°; the plots indicate the mean fiber angle for each bin. (B) The healing structure was remodeled as each fibroblast iteratively reoriented, migrated, deposited collagen, and removed collagen, according to the prescribed sequence shown.

Simulations were run as follows: after prescribing an initially random cell orientation distribution and collagen orientation distribution, we loop through all cells one at a time (in randomized order) with each cell reorienting according to a global mechanical cue and a local collagen structural cue (described in Eq.’s 1–4), then migrating a prescribed distance parallel to its new orientation. Collagen content was then added and removed from each element’s fiber orientation distribution according to Eq. 5, and the simulation proceeded to the next time step (1hr) to repeat this process. This simulation progression is depicted in Figure 1. For all simulation cases, we initiated the structure with randomly oriented collagen and randomly oriented cells, simulated 8 weeks of remodeling under strain levels between 0–10% engineering strain, and then compared the final steady-state collagen structures. Since we focused on steady-state properties rather than detailed temporal dynamics, we did not include cell proliferation (total cell density was held constant).

2.2. Agent-Based Model Rules and Modifications from Prior Published Version

Our previously published model was fit to myocardial infarct remodeling data (Rouillard and Holmes 2012). To adapt the myocardial infarct model for this tendon study, we refit cell density and collagen turnover parameters to match experimental data measured during healing in the rat supraspinatus tendon after surgical dissection and repair (Thomopoulos et al. 2003; Galatz et al. 2006). All model parameter values are reported in Table 1 below.

Table 1:

Model parameter values

Parameter	Baseline Value
Simulation domain	1mm × 1mm
Fibroblast number	3000
Fibroblast radius	5μm
Collagen element size	10μm × 10μm
Alignment adjustment, ρadj	0.888
Fibroblast migration speed	10μm per hr
Deposition rate, $k_{baseline}^{dep}$	1.008e−5 per cell per hr
Removal rate, $k_{baseline}^{rem}$	1.26% per hr
Strain-dependent deposition, $k^{sig}$	200
Collagen damage scaling, a	1
Collagen damage slope, b	30
Collagen damage threshold, εthr	5%

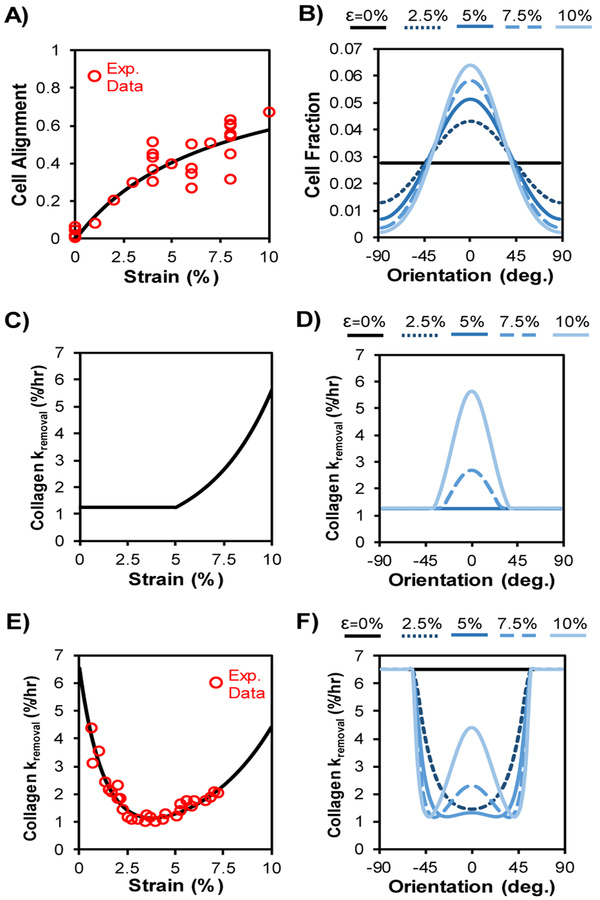
The orientation for each cell at each time-step depended on both strain and collagen alignment magnitudes. The parameter strain cue magnitude, SM, described the strength of cell alignment expected at any strain, and was obtained from a fit to experimental data from cell-stretching studies according to Eq. 1:

$$SM=\frac{\Delta \epsilon }{\Delta \epsilon +0.07376}$$ Eq. 1

where Δε is max principal engineering strain minus strain in the transverse direction, and 0.07376 is a constant derived by fitting experimental data (Wang and Grood 2000; Neidlinger-Wilke et al. 2001, 2002; Loesberg et al. 2005; Zhang et al. 2008; Houtchens et al. 2008; Ahmed et al. 2010; Prodanov et al. 2010; Chen et al. 2013; Tamiello et al. 2015; Kim et al. 2016) (Figure 2A). These experimental data were collected from studies that seeded cells on elastic membranes subjected to simple uniaxial strain at 1Hz frequency. To calculate a consistent cell alignment measure from each of these studies, we used the various alignment metrics reported to infer consistent wrapped normal cell orientation distributions for each strain value in each study. We then calculated alignment as the mean vector lengths (MVLs) of those inferred distributions.

Fig. 2. Cell alignment and collagen removal depend on strain.

(A) Cell alignment increased as a function of maximum principal engineering strain according to Eq. 1, fit to published experimental data (Wang and Grood 2000; Neidlinger-Wilke et al. 2001, 2002; Loesberg et al. 2005; Zhang et al. 2008; Houtchens et al. 2008; Ahmed et al. 2010; Prodanov et al. 2010; Chen et al. 2013; Tamiello et al. 2015; Kim et al. 2016). (B) Cell orientation probability distribution was set as a wrapped normal distribution according to Eq. 4 and the strength of alignment cues; curves shown here indicate the distributions that would be observed in response to the strain levels indicated, in the absence of any matrix alignment cues. (C) For strain-dependent damage simulations, we assumed collagen damage exponentially increased the rate of removal of fibers experiencing strain above a damage threshold according to Eq. 8. (D) Since fiber strain depended on orientation, collagen damage resulted in preferential removal of fibers oriented near the global tissue strain direction, as indicated by higher values of kremoval for those orientation bins. (E) For strain-dependent enzymatic degradation simulations, we fit previous experimental measurements that demonstrated collagen degradation by proteases depends nonlinearly on strain according to Eq. 9 (Huang and Yannas 1977). (F) Simulated uniaxial stretch led to different fiber strains for fibers with different orientations, which together with the nonlinear curve in (E) yielded varying distributions of kremoval for different applied strains.

The parameter collagen cue magnitude, CM, described the strength of cell alignment to local collagen fibers (i.e., the strength of contact guidance), and was set equal to local collagen mean vector length according to Eq. 2:

$$CM=ColMVL=\frac{1}{{\sum }_{i=1}^{N}Co{l}_i}\cdot \sqrt{{\left({\displaystyle \sum _{i=1}^N\left[Co{l}_i\cdot \cos \left({2\theta }_i\right)\right]}\right)}^2+{\left({\displaystyle \sum _{i=1}^N\left[Co{l}_i\cdot \sin \left({20}_i\right)\right]}\right)}^2}$$ Eq. 2

where Col_i is the amount of collagen oriented in each direction θι. An underlying assumption of this CM equation is that, in the absence of other cues, cells will align to the same extent as their underlying collagen. Both SM and CM theoretically ranged from 0 (corresponding to no alignment) to 1 (corresponding to perfect alignment), and the resultant combined cell alignment strength, ρ, was set according to Eq. 3 as a synergistic combination of the two orientation cues:

$$\rho ={\rho }_{adj}\cdot \left(SM+CM-SM*CM\right)$$ Eq. 3

where ρ_adj is an adjustment term that was also added to represent how strongly cells respond to the resultant orientation cue. This parameter was fit to match experimentally-reported collagen alignment in tendons healing under baseline loading (Thomopoulos et al. 2003).

After computing the cell alignment strength, ρ, the cell orientation angle was calculated by randomly selecting from a wrapped-normal probability distribution with a mean orientation angle and the alignment strength, ρ. The resulting cell orientation probability distribution was given by Eq. 4:

$$CellPro{b}_i=\frac{1}{\sqrt{-4\pi \text{ln}({\rho }^{0.25})}}\cdot {\sum }_{k=-\infty }^{\infty }\left[e^{\left(\frac{{\left({\theta }_i+2\pi k\right)}^2}{4\text{ln}\left({\rho }^{0.25}\right)}\right)}+e^{\left(\frac{{\left({\theta }_i-\pi +2\pi k\right)}^2}{4\text{ln}\left({\rho }^{0.25}\right)}\right)}\right]$$ Eq. 4

where CellProb_i is the probability of a cell orienting at each angle, −90° < θ_ι < 90°.

After cell reorientation, collagen was deposited and degraded. For collagen turnover in each orientation bin −90° < θ_i < 90°, we assumed zeroth-order deposition by cells at a global strain-dependent rate, k^dep, in parallel to each cell’s orientation, and we assumed a first-order removal at a rate, $k_i^{rem}$, that depended on the level of fiber strain as outlined in the next section.

$$\frac{dCo{l}_i\left(t\right)}{dt}=k^{dep}\cdot Cel{l}_i\left(t\right)-k_i^{rem}\cdot Co{l}_i\left(t\right)$$ Eq. 5

where Cell_i is the number of cells oriented in each direction θ_i. Note that the experimental measurements of collagen content used to fit our model parameters were reported as histologic scores, and therefore the collagen content levels in our simulations reflect these semi-quantitative measures.

2.3. Modeling Strain-dependent Collagen Turnover

The goal of this study was to explore the effects of strain-dependent remodeling of collagen during tendon healing. To calculate fiber strain as a function of orientation and global tissue strain, we assumed that collagen fibers undergo affine deformation, such that stretch, λ_i, in any direction depends on the unit direction vector, ${\stackrel{\rightharpoonup }{M}}_l$, and the right Cauchy-Green deformation tensor, $\tilde{C}$, according to Eq. 6.

$${\lambda }_i^2={\stackrel{\rightharpoonup }{M}}_l\cdot \tilde{C}\cdot {\stackrel{\rightharpoonup }{M}}_l$$ Eq. 6

We assumed the tissue experiences uniaxial extension with transverse thinning due to incompressibility, and no shears, so that fiber strain, ${\epsilon }_i^{fiber}$, depends only on fiber orientation, θ, and tissue strain, ε, according to Eq. 7 (note: we are using engineering strain ε=λ−1).

$${\epsilon }_i^{fiber}=1-\sqrt{{\left(\epsilon +1\right)}^2\cdot {\cos }^2\left({\theta }_i\right)+\frac{1}{{\left(\epsilon +1\right)}^4}\cdot {\sin }^2\left({\theta }_i\right)}$$ Eq. 7

We explored the effects of two forms of strain-dependent fiber removal. First, for strain-dependent damage simulations, we assumed that above a strain threshold, ε_thr, fibers are increasingly damaged and removed according to Eq. 8 (Figure 2 C-D).

$$k_i^{rem}=a\cdot k_{baseline}^{rem}\cdot \{\begin{array}{c}1for{\epsilon }_i^{fiber}\le {\epsilon }_{thr}\\ e^{b\cdot \left({\epsilon }_i^{fiber}-{\epsilon }_{thr}\right)}for{\epsilon }_i^{fiber}>{\epsilon }_{thr}\end{array}$$ Eq. 8

Where $k_{baseline}^{rem}$ is the baseline fiber removal rate fit to collagen content data in healing tendon experiments (Galatz et al. 2006), and a and b are scaling parameters, which were used to explore the model’s sensitivity to this damage relationship.

Second, for strain-dependent enzymatic degradation, previously reported experimental data suggested that fiber degradation decreases with load to a point, then begins to increase with load above that point (Huang and Yannas 1977; Ghazanfari et al. 2016). We fit this experimental data with a double exponential relationship given by Eq. 9 (Figure 2 E-F).

$$k_i^{rem}=k_{baseline}^{rem}\cdot \left(4.71e^{-81.4\cdot {\epsilon }_i^{fiber}}+0.248e^{26.0\cdot {\epsilon }_i^{fiber}}\right)$$ Eq. 9

For strain-dependent deposition of collagen, we assumed a sigmoidal relationship given by Eq. 10, wherein collagen expression doubles from no strain to 10% strain. This assumption was based on previous experimental reports that measured collagen I and collagen III expression after subjecting fibroblasts to various strain levels in vitro (Carver et al. 1991; Butt and Bishop 1997; Parsons et al. 1999; Lee et al. 1999; Breen 2000; Kim et al. 2002; He et al. 2004; Atance et al. 2004; Yang et al. 2004; Loesberg et al. 2005; Shalaw et al. 2006; Husse et al. 2007; Tetsunaga et al. 2009; Kanazawa et al. 2009; Blaauboer et al. 2011; Miyake et al. 2011; Galie et al. 2011; Petersen et al. 2012; Huang et al. 2013; Watson et al. 2014; Liu et al. 2016; Manuyakorn et al. 2016; Jiang et al. 2016). The vast majority of these studies observed that collagen levels were increased ≤ 2-fold.

$$k^{dep}=k_{baseline}^{dep}\cdot \frac{2}{3}\cdot \left(\frac{1}{1+e^{\left(-k^{sig}\cdot \left(\epsilon -0.05\right)\right)}}+1\right)$$ Eq. 10

Where $k_{baseline}^{rem}$to collagen content data in healing tendon experiments (Galatz et al. 2006), and k^sig is the sigmoidal slope parameter, which was varied to explore the model’s sensitivity to this deposition relationship. Note that this strain-dependent deposition equation assumed that cells responded to global strain rather than local affine strains based on each cell’s orientation.

3. RESULTS

3.1. Baseline Collagen Remodeling

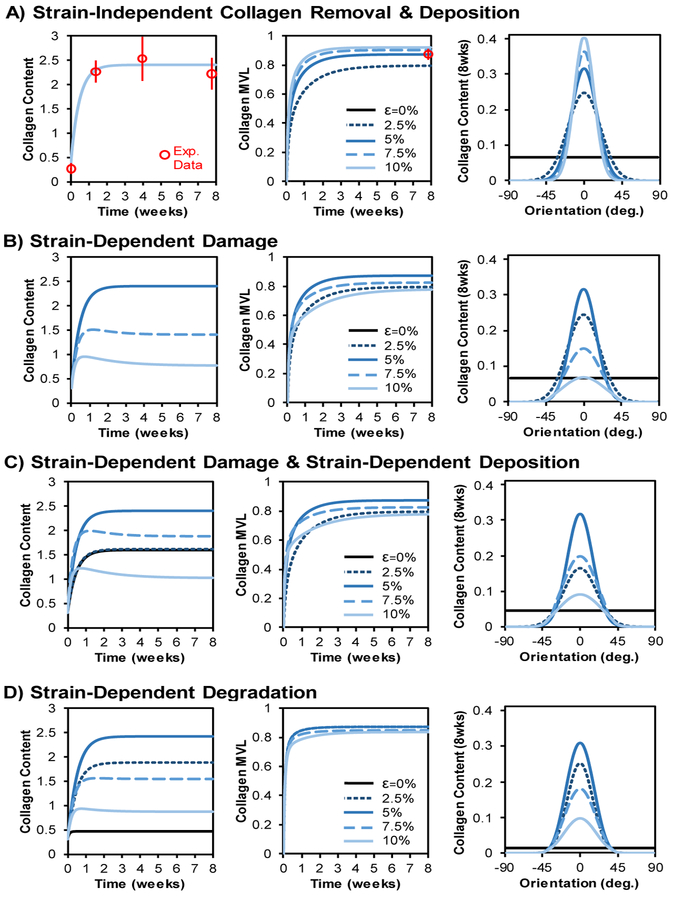
For the baseline simulation, we fit collagen turnover parameters to match experimental data measured in healing rat supraspinatus tendons, specifically matching the intermediate level of strain in our model (5% strain) to experimental measurements from the intermediate loading group (cage activity) in (Thomopoulos et al. 2003; Galatz et al. 2006). This parameter fitting enabled our baseline simulation at 5% strain without strain-dependent damage or degradation to closely follow the experimentally-observed collagen content and alignment (Figure 3A). Increasing strain levels across 0–10% resulted in increased alignments of both cells and collagen, and simulations reached steady state well before the 8-week time-point that we used for subsequent comparisons.

Fig. 3. Effect of collagen damage on long-term remodeling.

(A) With constant cell number, initial randomly-oriented cells, initial randomly-oriented collagen, and strain-independent collagen removal, increasing strain led to increasing collagen alignment over time (reported as mean vector length, MVL). Distributions reached steady state within ∼2 weeks and closely matched experimental reports (experimental mean +/− st. dev. are shown in red) of collagen content time-course (left panel) and long-term collagen alignment (middle panel) (Thomopoulos et al. 2003; Galatz et al. 2006). (B) Introducing strain-dependent collagen removal via damage above a strain-threshold caused decreases in both steady-state content and alignment in tissues experiencing strains above the damage threshold. Note that 0% and 2.5% strains yield the same content as 5%, so these curves are indistinguishable in the left panel. (C) Adding strain-dependent collagen deposition increased collagen content at higher strains but had no effect on steady-state collagen alignment values. (D) Simulations of strain-dependent collagen removal via degradation predicted biphasic content and alignment responses with steady-state content and alignment increasing at low strains and then decreasing at high strains.

3.2. Effect of Strain-Dependent Fiber Damage

Not surprisingly, introducing strain-dependent fiber damage (Figure 3B and 4B) had no effect at strains below the damage threshold. However, simulations at strains above the damage threshold predicted decreases in collagen content and collagen alignment as strain increased. Therefore, peak alignment occurred exactly at the strain level equal to the damage threshold, and peak content occurred at strains less than and equal to the damage threshold.

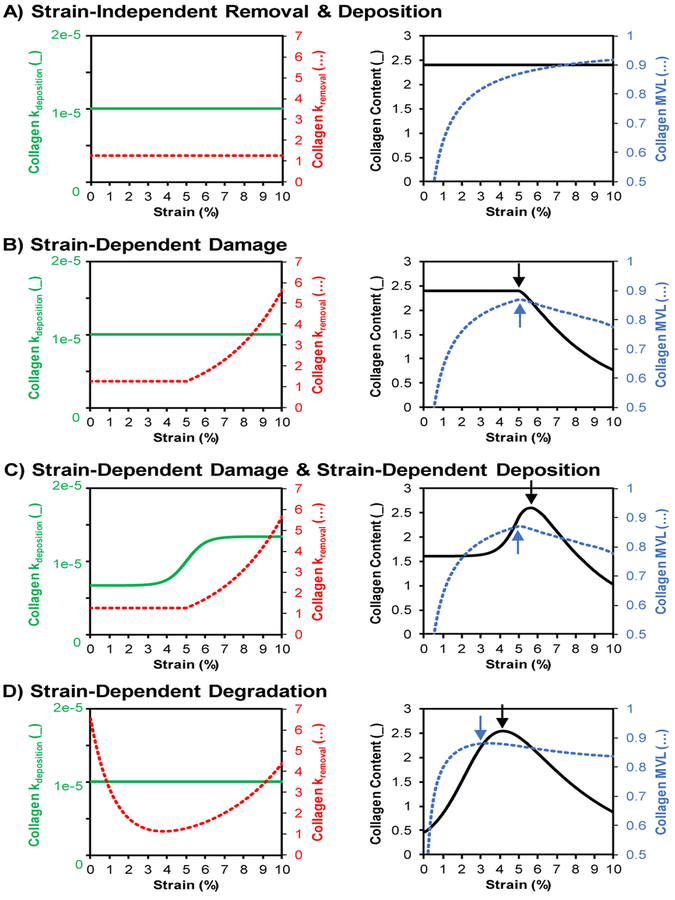
Fig. 4. Strain-dependent collagen turnover drives divergence of content and alignment.

Summary of the simulated changes in collagen deposition and degradation rates (left panels) and resulting steady-state collagen content and alignment outputs (right panels) as a function of global applied uniaxial strain. (A) Uniform, strain-independent collagen removal and deposition resulted in uniform steady-state content and increasing steady-state alignment as strain increased. (B) Introducing strain-dependent damage resulted in decreased content and alignment above the strain-threshold for damage. (C) Combining strain-dependent deposition with strain-dependent damage produced a strain regime where alignment is decreasing while content is still increasing. (D) Simulations of strain-dependent degradation also resulted in divergence of steady-state alignment and content peaks. Notably, this divergence occurred even without the addition of strain-dependent deposition. (Note (_) signifies the solid lines corresponding to the left vertical axis in each panel while (…) signifies the dotted lines corresponding to the right vertical axis.)

Experiments have shown that increased strain levels in healing tendons result in decreased alignment but increased total content (Thomopoulos et al. 2003; Galatz et al. 2009). A possible mechanism for increased content with load is strain-induced stimulation of collagen deposition by fibroblasts: many in vitro experiments have shown that mechanical strain can indeed increase collagen expression and secretion by fibroblasts (Butt and Bishop 1997; Lee et al. 1999; Papakrivopoulou et al. 2004; Atance et al. 2004; Husse et al. 2007; Balestrini and Billiar 2009; Guo et al. 2013; Watson et al. 2014). We repeated strain-dependent damage simulations with the addition of a strain-dependent deposition relationship such that deposition increased with increasing strain in a sigmoidal fashion (Figure 3C and 4C). Combining strain-dependent damage with strain-dependent deposition had no effect on steady-state alignment levels; however, the sigmoidal deposition led to a steady-state content vs. strain relationship with a peak content that now occurred at a strain level slightly higher than the damage threshold (Figure 4C). Importantly, this shift in the content peak produced a strain range with structural divergence, wherein alignment decreased with strain, but content increased with strain.

3.3. Effect of Strain-Dependent Degradation

As an alternative to strain-induced fiber damage, we also explored the effect of strain-dependent enzymatic degradation on long-term collagen content and fiber alignment. Previous experiments have shown that increasing strains can reduce protease-mediated degradation of collagen at intermediate strains, with a minimum degradation rate of ∼4% strain (Figure 2E) (Huang and Yannas 1977). Simulating the effect of this strain-dependent degradation across a range of tissue strains led to corresponding biphasic responses in both steady-state content and alignment (Figure 3D and 4D). Interestingly, peak alignment occurred at a slightly lower strain level than peak content occurred, thereby producing structural divergence even without including any strain-dependent deposition.

3.4. Divergence of Collagen Content and Alignment Peaks

In healing tendons subjected to variable loading conditions, published reports suggest that higher loads simultaneously increased content yet decreased alignment (Thomopoulos et al. 2003; Galatz et al. 2009). Our simulations predicted that one potential mechanism for this structural divergence is strain-dependent damage in combination with strain-dependent deposition. Specifically, increased strain induced higher damage and removal of fibers parallel to the strain direction, thereby decreasing alignment at strains above the damage threshold (Figure 4C). However, higher strains also induced greater production of fibers via strain-dependent deposition, and this increased deposition produced a net positive change in total collagen content.

Our simulations also identified strain-dependent degradation as a second mechanism that could give rise to structural divergence. The previously reported nonlinear degradation vs. strain relationship resulted in distinct steady-state alignment vs. strain and content vs. strain relationships (Figure 4D). Collagen alignment peaked at approximately the same strain level that gave the minimum fiber removal rate (i.e., the trough in Figure 2E). Further increasing strain from that point produced minimal changes in degradation rates of fibers that were nearly parallel to the strain (e.g., compare the −10° to 10° range between 2.5% vs. 5% curves in Figure 2F) while the same strain increase produced substantially decreased degradation of fibers that were more off-axis (−50° to −10°, or 10° to 50° in Figure 2F). These changes resulted in final collagen distributions with lower alignment but higher total content within a strain range near the trough of the degradation curve (Figure 4D).

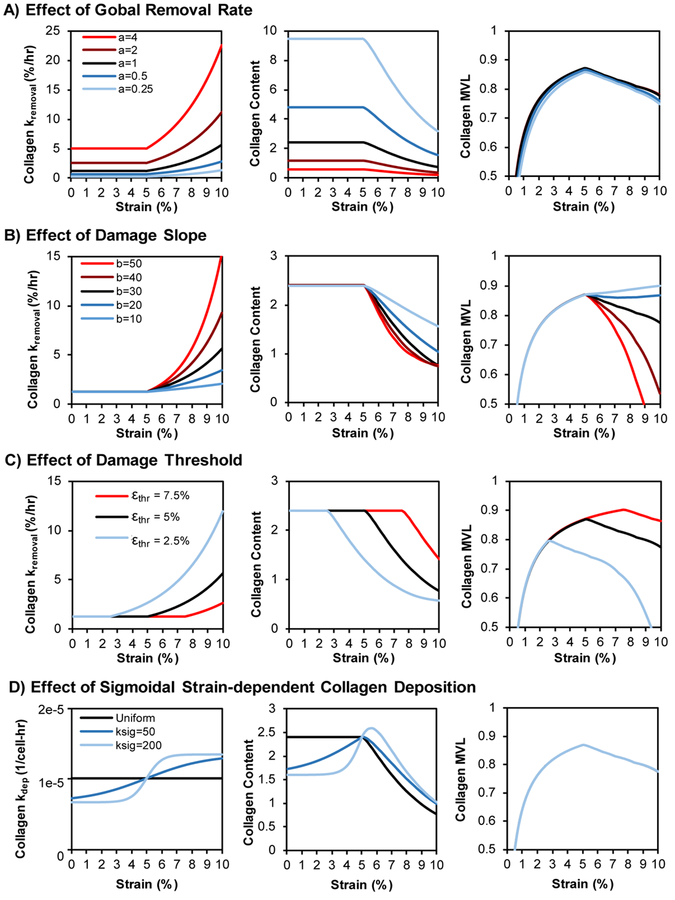
3.5. Parameter Sensitivity

While our curve for strain-dependent degradation was fit directly to experimental measurements (Eq. 9), the curves for strain-dependent damage (Eq. 8) and strain-dependent deposition (Eq. 10) were less constrained by existing experimental data. To explore the effects of these equation parameters, we tested the effects of varying damage threshold, damage severity, total removal rate, and sigmoidal deposition relationships vs. strain (Figure 5). Scaling global removal rate (Figure 5A) inversely scaled collagen content in linear fashion, i.e., doubling global removal cuts long-term content in half, but had negligible effects on collagen alignment. Scaling the slope (i.e., severity) of the damage curve above the threshold inversely scaled both content and alignment such that more severe damage further reduced content and alignment (Figure 5B). Shifting the damage threshold to lower or higher strains correspondingly shifted both content and alignment curves to lower or higher strains (Figure 5C). Across all of these simulations, the most consistent finding was that if collagen alignment peaked, then the peak always occurred at the same strain level as the damage threshold.

Fig. 5. Effect of damage and deposition parameters on steady-state content and alignment.

(A) Increasing the overall removal rate had minimal effect on collagen alignment at 8 weeks but had an inverse and proportional effect on collagen content across all strain levels (i.e., doubling the removal rate cut the steady-state content in half). (B) Increasing the slope (i.e. severity) of damage above the damage threshold decreased both collagen content and collagen alignment but did so non-uniformly. (C) Shifting the damage threshold to lower or higher strains caused corresponding shifts in the content and alignment vs. strain curves. (D) Combining strain-dependent deposition with strain-dependent fiber damage produced no change in steady-state alignment but changed the shape of the steady-state content vs. strain curve; a steep sigmoidal curve produced a clear divergence between alignment and content responses.

As was the case with scaling global collagen removal rates, adding strain-dependent deposition had no effect on alignment because deposition rate only altered the height but not the shape of the predicted collagen distributions (Figure 5D). However, the ability of the model to produce divergence between peak content strain and peak alignment strain depended strongly on the form of the deposition vs. strain curve: only very rapid transitions from minimum to maximum collagen production near the damage threshold produced noticeable divergence between the alignment and content peaks.

4. DISCUSSION

The goal of this study was to explore remodeling mechanisms that could explain the experimental observation that increased mechanical loading in healing tendons increases collagen content while decreases alignment. Our theoretical agent-based model simulations predicted that strain-induced collagen damage combined with strain-induced increases in collagen production can indeed give rise to divergence – i.e., a strain regime where increased strains yield increased content but decreased alignment – but only if there is a very sharp transition from low to high collagen deposition rates at exactly the right strain value. Experimental evidence strongly supports the idea that strain or load can modulate collagen synthesis: in vitro measurements of strain-dependent collagen deposition by fibroblasts typically show increases on the order of 2-fold from unloaded to highly loaded constructs (Butt and Bishop 1997; Lee et al. 1999; Papakrivopoulou et al. 2004; Atance et al. 2004; Husse et al. 2007; Balestrini and Billiar 2009; Guo et al. 2013; Watson et al. 2014), while increased loading of healing tendons in vivo (exercise vs. complete unloading) gives rise to ∼3-fold increases in matrix content (Thomopoulos et al. 2003; Galatz et al. 2009). However, it is less clear to what extent fiber damage actually occurs in the healing supraspinatus tendons that motivated our model (Thomopoulos et al. 2003; Galatz et al. 2006, 2009). Experimentally observed failure strains of collagen molecules and fibrils are upward of 40%, much higher than the fibril strains observed in rat supraspinatus tendons during normal motion (reported to be 4±5%) (Fratzl 2008; Connizzo et al. 2014). Zitnay and co-workers recently provided evidence of disruption of the collagen triple-helix above 8% strain in rat tail tendons under uniaxial stretch (Zitnay et al. 2017). This still exceeds the expected strains in normal supraspinatus tendon but seems plausible for individual collagen fibrils at the lower collagen densities found early in tendon healing.

As an alternative to strain-dependent damage, we also simulated the effects of strain-dependent variations in collagen degradation rates on long-term collagen structure. Previous experiments showed that strain modulates collagen degradation by proteases in vitro in a bi-phasic manner, with the lowest degradation rates at ∼4% strain (Huang and Yannas 1977). In our simulations, strain-dependent degradation at rates based on the Huang data gave rise to divergence of long-term collagen content and alignment. In contrast to our damage simulations, strain-dependent degradation produced this divergence without the need for strain-dependent modulation of collagen deposition. Furthermore, strain-dependent degradation has been experimentally shown to act in the range of strains experienced by fibers in the supraspinatus tendon (Connizzo et al. 2014). Based on these considerations, we consider strain-dependent degradation to be a more plausible explanation for the diverging content and alignment responses to load in healing tendons.

It is important to note the major assumptions and limitations in our current study. First, in the experimental models that motivated this work, increased loading was not constant throughout the healing time-course but intermittent (e.g., a daily controlled exercise regimen). It is unclear how long-term structure depends on these temporal dynamics, as well as the potential temporal dynamics of turnover rates throughout the healing time-course (e.g., inflammatory vs. fibrotic vs. remodeling phases). As a first-pass, we simulated simplified cases where collagen turnover rates, cell number, and mechanics were assumed to be constant throughout the 8-week healing period. Future simulations should account for temporal dynamics of these parameters. Second, we calculated fiber strains based on affine transformation from global tissue strains. While we believe this is a reasonable approximation on a global tissue scale, it is possible that complex network interactions within the interconnected fiber structure give rise to non-affine deformations and lead to some fibers deforming more or less than the bulk tissue. Third, while we simulated the effect of strain-dependent deposition, we assumed this cell response was a function of global strain and did not depend on each cell’s local orientation. Fourth, cell culture experiments have shown that mechanical loading can also modify cell proliferation (Sawaguchi et al. 2010; Richardson et al. 2013; Sun et al. 2016). We did not include strain-induced proliferation in our model as past measurements in the supraspinatus tendon showed subtle decreases in cell density with increased levels of loading (Thomopoulos et al. 2003; Galatz et al. 2009).

In summary, our model simulations suggested that multiple collagen remodeling mechanisms can theoretically give rise to the previously reported divergence of collagen content and alignment in healing tendons at higher loads: (1) biphasic strain-dependent degradation, or (2) strain-dependent damage in combination with simultaneous strain-dependent deposition. These findings suggest that future experiments should seek to isolate the potential effects of each mechanism in order to test its respective contribution to the evolution of collagen structure in healing tendons. Such experiments could include subjecting tendons to various loads with and without inhibitors of protease-mediated degradation, subjecting decellularized tendons to increasing loads, or using recently-developed reporters of collagen damage via fluorescent peptides that bind only to damaged collagen molecules (Zitnay et al. 2017).