Figure - PMC

Skip to main content

An official website of the United States government

Here's how you know

Here's how you know

Official websites use .gov
A .gov website belongs to an official government organization in the United States.

Secure .gov websites use HTTPS
A lock ( ) or https:// means you've safely connected to the .gov website. Share sensitive information only on official, secure websites.

View full-text article in PMC

. 2019 Jan 18;9:211. doi: 10.1038/s41598-018-36285-4

Search in PMC
Search in PubMed
View in NLM Catalog
Add to search

© The Author(s) 2019

Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.

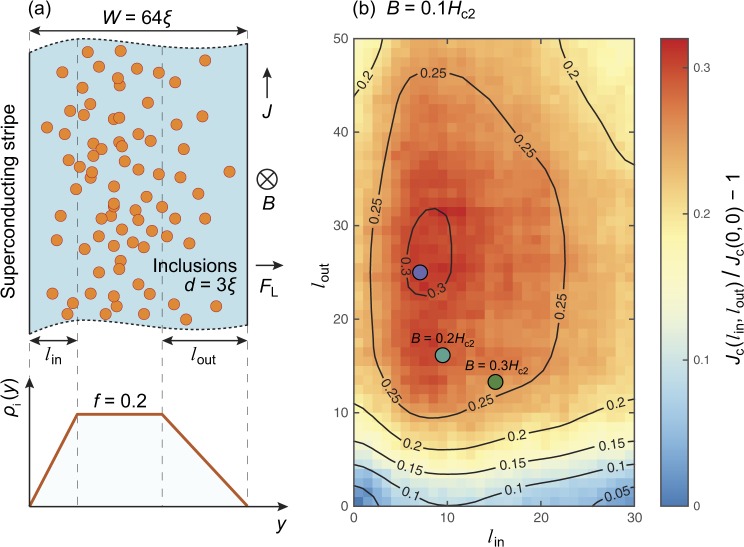
PMC Copyright notice

(a) Two-dimensional superconducting strip of width W = 64ξ with non-homogeneous inclusion distribution. The current J is applied vertically (along the x-axis), the magnetic field B is perpendicular to the figure plane, and the resulting Lorentz force F_L acts to the right (along the y-axis). The sample has a length of L = 1024ξ with quasi-periodic boundary conditions in the x direction; in the y direction, we have open boundary conditions, i.e., superconductor-vacuum surfaces. The strip contains (uncorrelated) randomly placed circular inclusions of diameter d = 3ξ. The density of these inclusions depends on y: in the middle of the sample, the volume fraction occupied by inclusions is f = 0.2, which corresponds approximately to conditions for the maximum possible critical current density in bulk samples. The density of the inclusion ρ_i(y) decreases linearly near the sample boundaries (see bottom plot): within a region of width l_in at the boundary where vortices enter the sample and l_out at the boundary where vortices leave the sample. (b) The critical current J_c as a function of l_in and l_out normalized by J_c(0, 0) at applied magnetic field B = 0.1H_c2. The critical current is increased by ~30% for finite l_in and l_out compared to the critical current from a homogeneous defect distribution (l_in = l_out = 0). The values of l_in and l_out corresponding to the maximum of the critical current J_c(l_in, l_out) are shown by colored circles for B = 0.1H_c2, 0.2H_c2, and 0.3H_c2. The effect is asymmetric and depends on the direction of vortex motion. The maximum is indicated by a (blue) circle. Corresponding maxima for fields 0.2H_c2 and 0.3H_c2 are indicated by (cyan and green) circles, marked by the field value.