Climate impacts on blacklegged tick host-seeking behavior

Abstract

The nymph of the blacklegged tick (Ixodes scapularis), the primary North American vector of the causative agent of Lyme disease, must attach to a host by the end of its questing season in order to feed and subsequently molt into an adult. The proper timing of this behavior is critical both for the tick’s survival and for perpetuating the transmission of tick-borne pathogens. Questing also depletes limited nymphal lipid reserves and increases desiccation risk. Given this tradeoff, questing behavior and its environmental influences can be expressed in a dynamic state variable model. We develop what we believe to be the first such model for a tick, and investigate the influence of climate on nymph fitness predictions. We apply these results to the hypothesized inland migration of I. scapularis from island refugia, evaluating fitness under suboptimal questing strategies and uncertain environmental conditions.

1. Introduction

The blacklegged tick (Ixodes scapularis) is the primary vector of Borrelia burgdorferi sensu stricto (hereafter B. burgdorferi), the causative agent of Lyme disease in the eastern US, and of six other emerging pathogens (Piesman, 2002; Nelder et al., 2016). The tick has three non-egg life stages over the span of two or more years – hatching as a larva, molting into a nymph, and finally molting again into an adult – but it is the nymphal instar that poses the greatest threat to humans, in part because it is active during months of peak outdoor human activity (Mather et al., 1996; Falco et al., 1999). Larval ticks become infected with B. burgdorferi and other horizontally transmitted pathogens during their first bloodmeal and transmit the infection to the next host after molting into nymphs and overwintering. The probability that a fed larva survives and finds a host as a nymph has been found to be the single most important determinant of pathogen survival using loop analysis (Davis and Bent, 2011; Dunn et al., 2013). The value of this probability in nature and its ecological determinants are, however, mostly unknown.

Here, we focused on how climate affects the timing and success of nymphal hostseeking. Defining this relationship may help explain or predict changing tick behavior over the course of a season under a variable climate, variations in tick behavior between regions with differing climates, and alterations in tick behavior and fitness under climate change or following migration to a new region.

As it is classically framed, the act of host-seeking, or “questing,” requires the tick to climb from relatively sheltered leaf litter, where it spends the majority of its life off-host, onto emergent vegetation that exposes it to the surrounding air. In so doing, the tick depletes its limited energy reserves (in the form of stored lipids) and risks desiccation (Needham and Teel, 1991). Each nymph must take a single bloodmeal, and must do so while the combination of local weather conditions and host availability make questing feasible (roughly between late March and early October in the northeastern US (Gatewood et al., 2009). Properly timing questing behavior is therefore critical for the tick’s survival and, in the case of nymphs, for the survival of B. burgdorferi.

Off-host hard tick behavioral decisions can be described as a tradeoff. The probability of finding a host is set against water and energy costs, the respective values of which vary with environmental conditions. Originally theorized by Lees (1946), this framework has subsequently been empirically supported by evidence that tick activity quickly exhausts lipid reserves, and that hard ticks perform diurnal vertical migrations suggestive of changes in the tick’s internal water state (Lees and Milne, 1951). Other authors have since referenced this basic model with little revision (Belozerov, 1982; Needham and Teel, 1991).

Due to the likely intense selection pressure exerted on questing and the tradeoff between costs and rewards that underlies it, tick foraging behavior is tractable by dynamic programming methods. Dynamic state variable models are widely used to investigate optimal foraging strategies that account for animals’ environmental conditions and internal state variables (Houston and McNamara, 1999; Clark and Mangel, 2000). Versions of these models have been constructed for arthropod vectors that adhere to a micropredator strategy (i.e., parasites that require multiple host individuals per generation) (Anderson and Roitberg, 1999; Ma and Roitberg, 2008), and the notion of optimality in parasite behavior has been raised more generally (Kelly and Thompson, 2000; Thomas et al., 2002). We are, however, aware of only one dynamic state variable model of a directly transmitted parasite (i.e., a parasite that requires a single host individual per generation, as in the case of a single tick life stage), designed by Fenton and Rands (2004). Prior models of ixodid tick questing have not explicitly included water or lipid reserves as state variables or developed biophysical models of water or energy usage, although they have considered the effects of temperature on development rates (Mount and Haile, 1989; Ogden et al., 2005; Dobson et al., 2011), direct effects of climate variables on questing (Mount and Haile, 1989; Ogden et al., 2005), and the effects of temperature and saturation deficit on survival (Corson et al., 2004).

We designed a dynamic state variable model of questing I. scapularis nymphs that makes explicit several common assumptions about the tradeoffs associated with questing. We then use this model to examine the theoretical impacts of climate on the behavior and fitness of I. scapularis, both for locally adapted (optimal) regional subpopulations and for ticks that have been exposed to new climates at a timescale that precludes full adaptation (suboptimal). In the latter category, it was hypothesized that ticks were confined to island relicts at the beginning of the 20^th century and reached the mainland in several invasions (Barbour and Fish, 1993): I. scapularis or Lyme disease were reported from Rhode Island (USA) by 1961 (Hyland and Mathewson, 1961), southern Connecticut (USA) by 1972 (Steere et al., 1977), southeastern Massachusetts (USA) in 1975 (Piesman and Spielman, 1979), central New Jersey (USA) in 1979 (Bowen et al., 1984), and Westchester County, New York (USA) in 1982 (Williams et al., 1986). From these early reported locations, it is proposed that these ticks have continued to spread inland into generally drier and warmer climates. We specifically considered this inland migration under various adaptation scenarios. Our analysis was entirely theoretical and based on known tick physiology and expert judgment. We hope the insights gained will help guide the design of experiments or field observations to validate the assumptions and predictions of the model.

2. Materials and methods

2.1. Dynamic state variable model

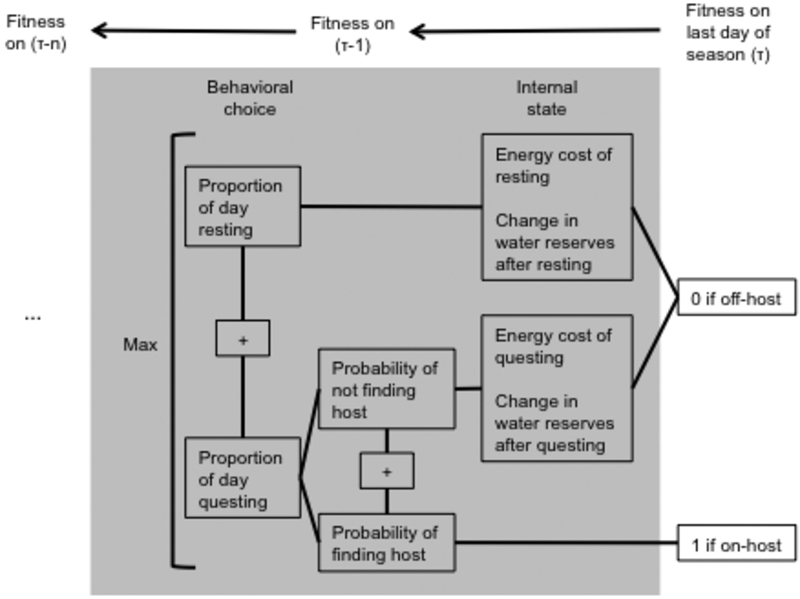
We use state-dependent dynamic programming to model how an I. scapularis nymph would maximize its probability of attaching to a host before the end of the season, subject to energy and water costs (state variables) and local climatic conditions and host density (environmental variables). For each day of the season and combination of state variables, the model determines the optimal proportion of the day the tick should spend questing, as opposed to remaining under the leaf litter. A matrix of optimal questing decisions and fitness values (defined as a tick's probability of finding a host from that time point until the end of the season) is calculated iteratively, starting with the final day of the season. We then explore the behavioral "paths" taken by individual ticks by running forward simulations from various starting state combinations, using the matrices generated by the backwards dynamic programming equation as lookup tables (Fig. 1) (Clark and Mangel, 2000; Fenton and Rands, 2004). Tables 1-3 summarize the variables, constants and functions described in the model below.

Fig. 1.

Model schematic. The dynamic programming equation defines a fitness reward for each tick life stage at the end of the season: 1 for on-host ticks, 0 for off-host. Fitness (defined as the overall probability of finding a host by the final day of the season t) on the penultimate day of the season is defined by calculating the probability of receiving each of these “rewards” under various values of p_q(t-1) (proportion of day t-1 spent questing) and then selecting the highest value. For a given p_q(t-1), a tick’s probability of finding a host is p_q(t-1)h_q(t-1) (where h_q(t) is the probability of finding a host on day t), while a tick’s probability of not finding a host is p_q(t-1)(1-h_q(t-1)). (These expressions assume the probability of finding a host while resting is 0). The total payoff associated with behavioral choice p_q(t-1) is the sum 1*p_q(t-1)h_q(t-1)+ 0*p_q(t-1)*(1-h_q(t-1)). The tick should choose p_q(t) to maximize the sum of these payoffs, meaning in this case that the tick will allocate all of its time to questing (p_q(t-1)=1). Fitness on day t-1 is therefore h_q(t-1). As time moves backwards, fitness on day t is dependent on the fitness on day t+1 of a tick with the internal state variables that are the result of the tick’s choices – because if a tick does not find a host, its internal state variables x and w (energy and water, respectively) change according to how much time it spent on each activity. Fitness is calculated (and maximized) for every combination of state variables on every day until the first day of the season.

Table 1.

Definitions of variables used in the dynamic state variable model

Variable	Definition
λ	Life stage
x	Lipid reserves (μg)
w	Water reserves (μg)
t	Day of season
pr(t),pq(t)	Proportion of day spent resting or questing, respectively
hr(t), hq(t)	Probability of encountering a host on day t while resting or questing, respectively
βr(t), βq(t)	Net change in water reserves (μg/day) on day t while resting or questing, respectively
aVr, aVr	Water vapor activity (RH/100) encountered while resting or questing, respectively
Tr, Tq	Temperature (K) encountered while resting or questing, respectively

Table 3.

Definitions of functions used in the dynamic state variable model

Function	Definition
R(λ, x, w)	End-of-season reward for life stage λ
H(x, w, t: pq(t))	Payoff for tick in state (x, w) at time t given pq(t)
V(λ, x, w, t)	Fitness of tick in life stage λ and state (x, w) at time t assuming optimal behavior
βN(aV, T, w)	Net hourly change in water reserves given climate variables (aV, T) and water reserves w (μg/hr)
βT(aV, T)	Proportion of water reserves lost per hour due to transpiration (hr−1) given climate variables (aV, T). Alternately notated βT
βG(aV, T, w)	Hourly water gain due to passive sorption (μg/hr) given climate variables (aV, T) and water reserves (w). Alternately notated βGn, where n corresponds to the subscripts of the water gain constants An and Bn
A(aV, T, w), B(aV, T, w)	Stepwise functions defining the ranges over which each βGn applies (μg/[hr*K], μg/hr)

As we only consider host-seeking in the nymphal life stage, we divide the tick life cycle into two life stages (λ) of interest: λ = N: off-host (nymph); and λ = A: on-host (adult, assuming 100% nymph feeding and molting success).

Life stage N has two state variables: lipid and water reserves. Lipid reserves are represented by the variable x in the range x_min < x < x_start, where x_min is a critical lipid level at or below which the animal dies, and x_start is the tick’s starting level of lipid reserves. x_start also represents a lipid maximum, as ticks have no way of replenishing lipids prior to finding a host. Water reserves are represented by the variable w in the range w_min < w < w_max, where w_min is a critical water level at or below which the animal dies and w_max is the tick's maximum level of water reserves.

If the nymph reaches day t - the end of the season - without finding a host, the terminal reward function is

$$R(N)=0$$ (1)

If the nymph has found a host, it has switched life stage to A, and we can assume it will survive (for simplicity, we define success in attaching to a host as independent of lipid and water reserves):

$$R(A)=1$$ (2)

Consider the fitness function V(λ,x,w,t), which calculates the probability that an optimally behaving tick at stage λ and time t with state variables x and w will find a host before the end of the season. It follows that the fitness function for the adult stage V(A,x,w,t) = R(A) for all t, because a tick does not need to make any further behavioral choices once it has found a suitable host.

The nymphs can allocate portions of each day p_r(t) and p_q(t) = (1 – p_r(t)) to two behaviors: r, rest/quiesce in leaf litter; or q, quest. Each behavior carries a probability that the tick will find a host by the end of day t. For simplicity, we define h_q, the probability of finding a host while questing, as a constant for all t and h_r, the probability of finding a host while resting, as 0 except where otherwise indicated.

Each behavior incurs daily energetic costs c_r and c_q – the daily rates of lipid loss associated with resting and questing, respectively. The portion of day t spent resting carries an energetic cost of c_rp_r(t), whereas the portion spent questing carries an energetic cost of c_qp_q(t). We ignore any energetic cost associated with transitioning between states.

Changes in water reserves are more complex, as the tick both gains and loses water with each behavior, dependent on the tick's current water reserves and local temperature and water vapor activity (relative humidity represented as a proportion rather than a percentage) (Wharton and Richards, 1978)). A given behavior on day t results in a net change in water reserves β_r(t) or β_q(t) (for resting and questing, respectively) according to the functions described in section 2.2.

Derivations of state variable parameters and functions are described in more detail below, in Supplementary Methods S1, and in Supplementary Tables S1-3. For both lipid and water functions, costs are drawn from normal distributions (with means defined as in Supplementary Methods S1) in order to minimize unrealistic outputs that can result from repeatedly incurring discretized costs and benefits in the setting of strictly defined thresholds (Houston and McNamara, 1999).

To determine how much time a tick should allocate to questing, we calculate the payoff H(x, w, t:p_q(t)) for decision p_q at time t given state variables x and w. The function is the sum H_A + H_N of the tick’s predicted off-host and on-host payoffs on day t+1.

If the tick ends day t on a host, the payoff is:

$$H_A=\left(h_r(t)p_r(t)+h_q(t)p_q(t)\right)\ast R(A)$$ (3)

The first expression (within the parentheses) represents the probability that the tick ends day t on a host and the second expression represents tick fitness once on that host. As discussed above, the on-host fitness function V(A,x,w,t) = R(A) for all t.

The payoff for a tick that ends the day without finding a host is calculated as:

$$\begin{array}{cc}\hfill & H_N=\left(1-\left(h_r(t)p_r(t)+h_q(t)p_q(t)\right)\right)\ast \hfill \\ \hfill & V\left(N,\max \left[(x-c_r{p}_r(t)-c_q{p}_q(t)),x_{min}\right],\max \left[\left(w+{\beta }_r(t)p_r(t)+{\beta }_q(t)p_q(t)\right),w_{min}\right],t+1\right)\hfill \end{array}$$ (4)

The expression (1 – (h_r(t)p_r(t) + h_q(t)p_q(t))) represents the probability that the tick ends day t without finding a host given behavioral choice p_q(t). The expression of the form V(N, x, w, t+1) represents the fitness of an off-host nymph on day t+1 after having incurred the water and energetic costs associated with behavioral choice p_q(t). The tick will maximize p_q(t), i.e. choose p_q(t) such that its fitness V(λ,x,w,t) is equal to the maximal possible payoff. Borrowing notation from Fenton and Rands (2004),

$$V(N,x,w,t)=\max \left[p_q(t)\right]H\left(x,w,t:p_q(t)\right)$$ (5)

with boundary conditions (minimum possible x and w)

$$V(N,x_{min},w,t)=0$$ (6)

$$V(N,x,w_{min},t)=0$$ (7)

We may also consider a tick population that has evolved under one set of conditions and subsequently moved to a second environment without changing its questing strategy. To model the resulting suboptimal behavior, we generate a tick optimally adapted to one climate but subjected to another, as calculated by:

$$V(N,x,w,t)=H\left(x,w,t+1:p_{q_{init}}(t)\right)$$ (8)

where p_qinit(t) is the questing proportion for a given set of state variables at time t that maximizes the payoff function in the initial scenario. We then calculate the payoffs at time t given state variables x and w as above.

Parameter calculations are conducted in Mathematica Ver. 9.0.1.4055646 (Wolfram Research, Champaign, Illinois, USA) and Igor Pro Ver. 6.3.7.2 (WaveMetrics, Lake Oswego, Oregon, USA). Simulations are run in Igor Pro. Igor Pro code and output are available at doi:10.17632/4vnt67pk63.1.

2.2. Ixodid water balance model

We define the tick’s net hourly change in water reserves as the piecewise function β_N(a_V,T,w), dependent on temperature T (in kelvins (K)), ambient water vapor activity a_V, and tick water reserves w:

$${\beta }_N(a_V,T,w)=\{\begin{array}{cc}{\beta }_G(a_V,T),\hfill & a_v\ge a_w\hfill \\ {\beta }_G(a_V,T)-w{\beta }_T(a_V,T),\hfill & a_v<a_w\hfill \end{array}\phantom{\}}$$ (9)

where β_T is the function describing the proportion of water reserves w lost due to transpiration per hour, and β_G is the function describing hourly water gain from the atmosphere (component functions described in more detail below). In most cases – i.e., when ambient water vapor activity is less than a_w, the activity of stored water in the tick -, β_N(a_V,T,w) is equal to the water gained by passive sorption minus the water lost to transpiration. When ambient water vapor activity equals or exceeds tick body water activity, the change in water reserves is determined by the water gain function alone, as no water is lost to transpiration.

2.2.1. Water loss

We model proportion of water reserves w lost due to transpiration per hour β_T(a_v,T) as a single-compartment transpiration process (Wharton and Richards, 1978):

$${\beta }_T(a_v,T)=k_T{T}^2\text{ln}(\frac{a_w}{a_v})$$ (10)

where k_T is a constant. T is squared to account for temperature’s linear relationship to both the diffusion gradient across the tick cuticle and cuticle permeability (Beament, 1959; Toolson, 1978). As shown in equation 9, rate of water loss in μg/hr is the product of the above formula and body water content w. This approach assumes single-compartment exchange across all humidities.

There is also evidence for a critical cuticle transition temperature (CCTT) at approximately 306.5 K in Ixodes ricinus, above which permeability increases by a factor of nearly 20 (Supplementary Fig. S1) (Beament, 1959). k_T takes on different values above and below this temperature. Unless otherwise indicated, all simulations below are conducted below the CCTT.

2.2.2. Water gain

Relatively little is known about tick water vapor absorption, although it has been demonstrated that hard ticks absorb water at their mouthparts, likely by secreting a hygroscopic solution (Rudolph and Knülle, 1974). Here, we model water uptake as passive sorption, assuming linear, non-saturable uptake kinetics as seen, for example, in Xenopsylla cheopis (O’Donnell and Machin, 1988), and linear dependence on T (Toolson, 1978):

$${\beta }_G(a_v,T,w)=a_{v}TA(a_V,T,w)+B(a_V,T,w)$$ (11)

where A(a_V, T, w) and B(a_V, T, w) are stepwise functions that define the values taken by slope A_n and intercept B_n over specific ranges of a_V, T, and w.

In order to allow the gain function to change with w, T and a_V, we define β_G(a_V, T,w) as a piecewise function. We use previously published rates of tick water gain and loss (Yoder and Spielman, 1992), taking into account two physiological thresholds. The tick's critical equilibrium activity (CEA), at a_V = 0.88, is the experimentally determined lowest water vapor activity at which an I. scapularis nymph is able to maintain constant water reserves (Yoder and Spielman, 1992). The tick’s pump threshold (PT) is the lowest water vapor activity at which a nymph can take up any water at all. (Historically, the term “pump threshold” is used for this value in reference to arthropods actively ‘pumping’ water against its concentration gradient, although we do not explicitly consider water vapor activity by ticks as an active, energy-requiring process). Below the PT, a tick loses water at a rate defined solely by the transpiration equation (equation 10). Based on previously published transpiration rate measurements and tick survival times, we set the PT equal to 0.75 (Supplementary Fig. S2) (O’Donnell and Machin, 1988; Yoder and Spielman, 1992; Stafford, 1994). In the equation below, we also introduce two new notations for convenience, abbreviating β_T(a_V,T) as β_T and defining β_Gn = a_vTA_n + B_n.

$${\beta }_G(a_V,T,w)=\{\begin{array}{cc}0,\hfill & w=w_{max}\hfill \\ {\beta }_{G_1},\hfill & w<w_{max}\cap a_v\ge a_w\hfill \\ {\beta }_{G_1},\hfill & w<w_{max}\cap CEA\le a_v<a_w\cap {\beta }_{G_1}-w{\beta }_T\ge {\beta }_{G_2}-w{\beta }_T\hfill \\ {\beta }_{G_2},\hfill & w<w_{max}\cap CEA\le a_v<a_w\cap {\beta }_{G_1}-w{\beta }_T<{\beta }_{G_2}-w{\beta }_T\hfill \\ {\beta }_{G_2},\hfill & w<w_{max}\cap PT\le a_v<CEA\cap {\beta }_{G_2}-w{\beta }_T<{\beta }_{G_3}-w{\beta }_T\hfill \\ {\beta }_{G_3},\hfill & w<w_{max}\cap PT\le a_v<CEA\cap {\beta }_{G_2}-w{\beta }_T\ge {\beta }_{G_3}-w{\beta }_T\hfill \\ 0,\hfill & w<w_{max}\cap a_v\le PT\hfill \end{array}\phantom{\}}$$ (12)

where ∩ denotes the intersection of two of more conditions. In brief, water gain is 0 when tick water reserves are at w_max or ambient water vapor activity lies below the PT. Otherwise, A_n and B_n adopt new values as ambient water vapor activity crosses a_w and the CEA. The conditions relating gain functions β_Gn to each other ensure that β_G(a_V,T, w) is continuous across all a_V and w, and that it is an increasing function of a_V (i.e., more humid environments are more hydrating).

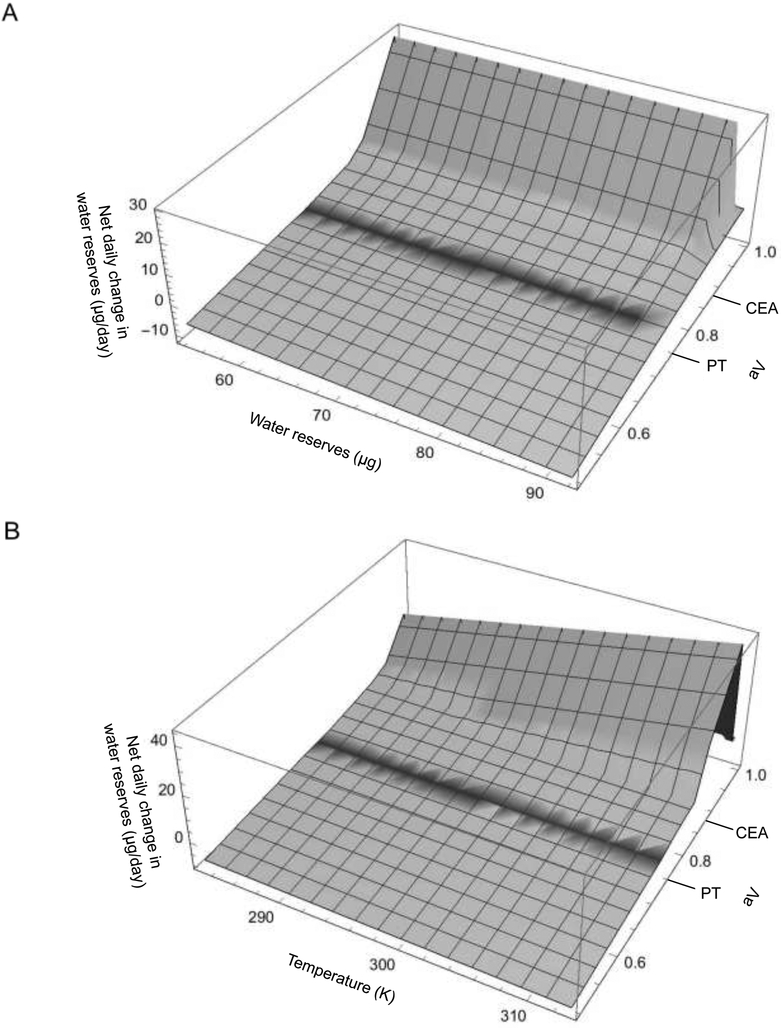
Fig. 2A depicts the resulting net daily change in tick water reserves over various starting levels of water reserves and water vapor activities at T = 296 K. Fig. 2B shows the net daily change in tick water reserves over various temperatures and water vapor activities at w = 72.5 μg. In expanding the formula for hourly net water change to daily net water change, the current model does not take into account changes in the sorption constants that occur within each 24 h period.

Fig. 2.

Daily water change (A) as a function of water vapor activity and a tick’s current water reserves at a constant temperature (296 kelvins (K)), and (B) as a function of water vapor activity and temperature with constant water reserves (72.5 μg); a_V, water vapor activity; PT, pump threshold; CEA, critical equilibrium activity

The water balance equation is a monotonically increasing function of water vapor activity, meaning increasing water vapor activity reduces the rate at which nymphs lose water (or increases the rate at which they gain water). The relationship of the change in water content to change in temperature $\frac{\delta \left(\frac{dw}{dt}\right)}{\delta T}$, however, changes over various thresholds.

Below the CCTT, increasing temperature is more desiccating when a_V<PT and less desiccating when a_V≥PT. Above the CCTT (after correcting the transpiration constant for increased cuticular permeability), increasing temperature only ceases to be more desiccating when a_V≥CEA (Supplementary Fig. S3). As a result of the piecewise definition of β_N(a_V,T,w), the derivative $\frac{\delta \left(\frac{dw}{dt}\right)}{\delta T}$ is discontinuous.

2.3. Accounting for uncertainty in tick knowledge of the environment

Equations 4 and 8 assume ticks have either complete knowledge of the new environment (optimal adaptation) or complete ignorance of the new environment (no adaptation), respectively. A tick population undergoing a regional or climatic transition, however, may be uncertain about its desiccation risk, knowing only that climate may conform to one of several scenarios. To define optimal phenotypic strategies at a population level in the face of this uncertainty, we make use of fitness sets as defined by Levins (1968). The technique considers the fitness of a spectrum of phenotypes under two (or more) environments. A phenotype’s fitness in each environment under consideration is plotted on its own axis. The resulting shape taken by the set of possible phenotypes indicates the ideal distribution of phenotypes in the population (or, more narrowly, of a set of siblings) under conditions in which it is uncertain whether the organism will encounter environment 1 or environment 2. A convex set indicates that an intermediate phenotype is fittest. A concave set indicates that all intermediate phenotypes are less well adapted than their more specialized counterparts, and that an optimal set of offspring will feature a mix of specialized phenotypes.

3. Results

We examine model output over a 20 day season, assuming constant temperature and humidity (longer seasons were considered, but early season behavior did not change with time). Because modeled nymphs have perfect knowledge of the end of the season and may successfully attach to a host regardless of lipid reserves, all nymphs under all conditions will quest 100% of the penultimate day of the season t-1 (Fig. 1). If the probability of encountering a host remains constant, an increasing array of tick state combinations will quest for increasing proportions of each day as the season approaches t.

3.1. Host availability influences questing

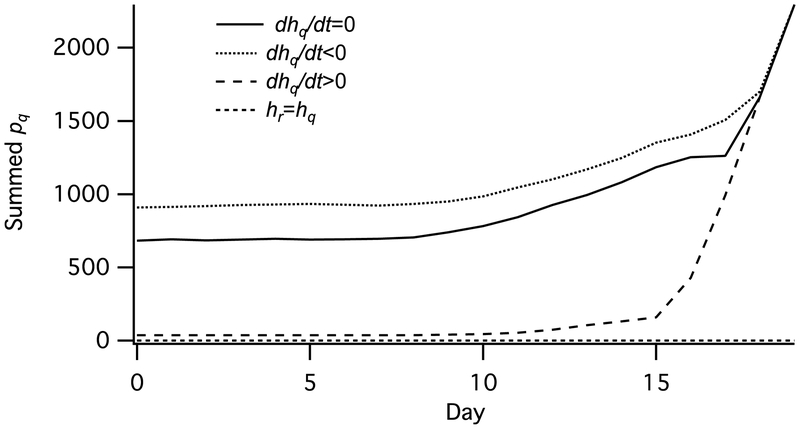
The probability of encountering a host while conducting a particular activity on day t is linearly related to the payoff function for each behavior. Absolute changes in this probability therefore directly impact fitness, with higher probabilities increasing fitness scores. Relative changes in h_q(t) and h_r(t) associated with a given day affect p_q(t), with higher h_q(t) increasing the proportion of time spent questing at time t (and higher h_r(t) increasing the proportion of time spent resting) across all state combinations (Fig. 3).

Fig. 3.

Tick questing behavior in relation to expected host encounter probability. Curves show the summed p_q(t) values (the proportion of day t spent questing) for all state combinations on each day for a constant, increasing and decreasing probability of encountering a host while questing, as well as for when the probability of encountering a host while resting is equal to that while questing. h_q and h_r are the probabilities of encountering a host while questing and resting, respectively, held constant for all t; dh_q/dt is the rate of change in h_q over time. For dh_q/dt=0, h_q=0.001 and h_r= 0; for dh_q/dt>0, h_q=5.5E-06+5.5E-06t and h_r= 0; for dh_q/dt<0 h_q=0.001-5.5E-06_t and h_r= 0; for h_r=h_q h_q=0.001 and h_r= 0.001.

Relative to a constant probability of finding a host while questing h_q(t), an h_q(t) that increases over the course of the season decreases questing early in the season, while a decreasing h_q(t) increases early questing. When the probability of finding a host while resting h_r(t) is increased above 0, p_q(t) decreases markedly, with p_q(t) = 0 when h_r = h_q. This alternate parameterization corresponds to a tick population that parasitizes hosts present in the leaf litter.

3.2. Local climate Influences questing

To evaluate the effects of water loss and gain on tick questing behavior, we generate optimal decision matrices for various combinations of leaf litter and air humidities. Our results fall into three qualitative categories of questing strategies.

3.2.1. If ticks lose water by questing and gain by resting, their strategy depends on multiple state variables

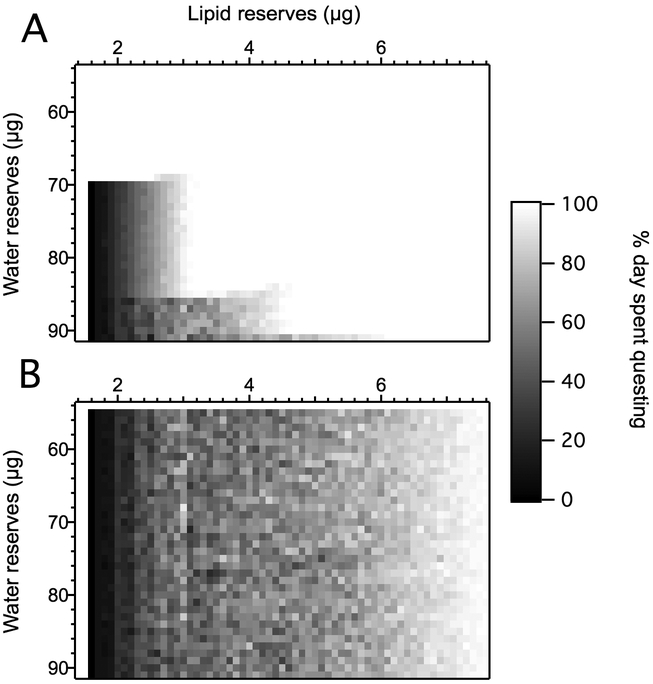
When air a_V < CEA < litter a_V, meaning that ticks are desiccated by questing but may replenish water reserves by resting, tick optimal behavior is dependent on day of season and lipid and water reserves (Fig. 4).

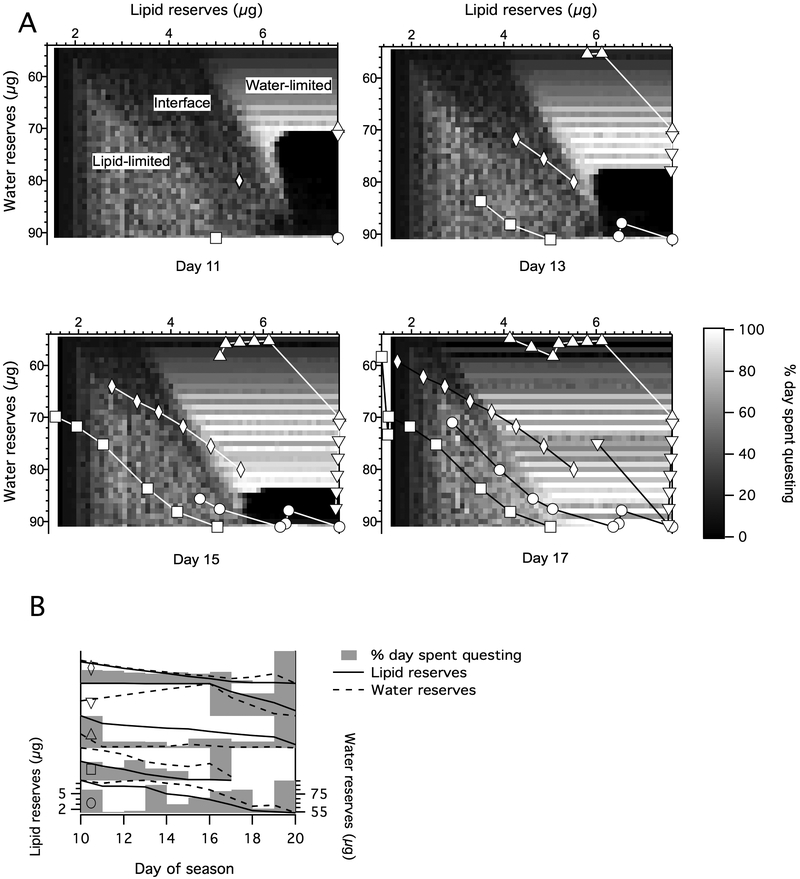
Fig. 4.

Representative model output when ticks lose water by questing and gain by resting: air a_V < CEA < litter a_V (T_q = 293 kelvins (K), a_Vq = 0.8, T_r= 293 K, a_Vr= 0.9). (A) p_q(t) heatmaps, where a_V is water vapor activity; CEA is the critical equilibrium activity; T_q and a_Vq are the temperature and water vapor activity above the leaf litter, respectively; T_r and a_Vr are the temperature and water vapor activity below the leaf litter, respectively; p_q(t) is the proportion of day t spent questing. Each cell represents an optimal behavioral decision given a specific combination of state variables on a given day. Shown here are the results for days 11, 13, 15 and 17 of a 20 day season, generated from the average of 10 stochastic runs. The horizontal axis indicates a tick’s lipid reserves in μg, the vertical axis represents its current water reserves in μg, and the shade of each cell represents the percentage of the day a tick with that combination of water and lipid reserves should allocate to questing (lighter meaning a larger percentage). In the heatmap corresponding to day 11, regions in which tick behavior is limited by water reserves, lipid reserves, or a combination are labeled. The superimposed pathlines (circle, square, triangle, inverted triangle and rhombus) represent the fates of individual ticks, each with different starting states, traversing this field of optimal behaviors. The ticks start day 11 with the combination of lipid and water reserves corresponding to the coordinates of each symbol. Each tick then quests according to the optimal behavior calculated for that cell, starting the following day with lipid and water reserves that have changed as a result of that behavior. This change is indicated by the movement of the tick’s corresponding symbol to a new set of coordinates within the state variable grid. Because the optimal strategy for a given state combination changes day by day, the field of optimal behaviors is updated, and the tick makes a new questing decision depending on the dictates of the cell it currently occupies. We traced the state changes of these five ticks from day 11 to day 17 by running forward simulations that used the averaged matrix of optimal behaviors as a lookup table. Forward runs use deterministic versions of the energy and water state variable equations incorporated into the backwards dynamic programming equation. (B) Alternate representation of the pathlines shown in A. Plots illustrate the percentage of time spent questing (gray bars), lipid reserves (solid lines), and water reserves (dashed lines) by day of the ticks corresponding to the appropriate symbols. Bars representing the percentage of the day spent questing are scaled so that 0% aligns with x_min and w_min and 100% is even with x_start and w_max, where x_min and x_startare the tick’s minimum and starting lipid reserves, respectively, and w_min and w_max are the tick’s minimum and maximum water reserves, respectively.

Heatmaps derived from this scenario depict the optimal proportion of the day spent questing for every possible tick state combination on a given day. They are divided into three spaces: a lipid-limited area in the lower left, a water-limited area in the upper right, and the diagonal interface between these.

Within the lipid-limited area, high-lipid ticks begin questing earliest in the season. The rate at which this high p_q(t) progresses “horizontally” over time to lower-lipid ticks is directly related to the parameters c_r and c_q. Ticks with lipid reserves equal to x_min are an exception, and allocate all time to questing on all days. This biologically unrealistic result is an artifact of the modeled tick’s perfect knowledge of its critical energy level.

In the water-limited area ticks quest little when their water reserves w are at or near w_min, and increase questing as w increases. The rate at which this high p_q(t) progresses “vertically” over time to more desiccated ticks is related to β_q(t) and β_r(t). An exception to this general pattern is a low-p_q(t) region in the figure that extends upwards (towards lower water reserves) from w_max −1. The low-p_q(t) region contracts towards w_max −1 as time progresses. Ticks starting below the low-p_q(t) region in Fig. 4 (i.e., ticks with higher water reserves) maintain water reserves at or near w_max until crossing into the lipid-limited area, effectively conserving water until their optimal questing strategy is no longer dependent on their water reserves (circle pathline in Fig. 4). Ticks starting within the low-p_q(t) region (ticks with moderate water reserves) gradually increase their water reserves, conserving water before questing within the water-limited area later in the season (inverted triangle pathline). Ticks starting above the low-p_q(t) region (ticks with lower water reserves) quest early and spend the rest of the season with low water reserves (triangle pathline).

The interface between the lipid- and water-limited areas is defined by two edges. On the lipid-limited side, the edge is a line through the origin, the slope of which is defined at each point by the expression:

$$\frac{\left({\beta }_r(t)p_{r_{opt}}(x,t)+{\beta }_q(t)p_{q_{opt}}(x,t)\right)}{-\left(c_r{p}_{r_{opt}}(x,t)+c_q{p}_{q_{opt}}(x,t)\right)}$$ (13)

where p_qopt(x, t) is the optimum p_q for ticks with lipid reserves x at time t (Supplementary Fig. S4). Ticks starting to the left of this edge (i.e., ticks starting the season with lower lipid reserves) will remain in the lipid-limited area until the end of the season and cannot cross back over into the interface region (square pathline). Less desiccating environments expand this lipid-limited area and decrease the slope at which ticks approach the origin (the lipid and water minima), allowing increased time for questing (rhombus pathline).

These geometric details, while revealing of the model’s structure, are unlikely to be ecologically relevant. Possible exceptions are situations that lead to rapid death by desiccation or failure to find a host prior to lipid exhaustion; these would include highly desiccating environments, water-depleted individual ticks, or late-season questing.

3.2.2. If ticks lose water regardless of behavior, they quest at nearly all times

When litter a_V < CEA, meaning the tick is unable to replenish water reserves by resting, the heatmap of optimal strategies is the same for all t < t (Fig. 5A). Under this scenario, nearly all state combinations quest 100% of the time. The remnants of the lipid-limited area and the diagonal interface still exist in the lower left corner, but are dominated by the water-limited area.

Fig. 5.

Alternative climate scenarios. (A) p_q(t) heatmap when ticks lose water regardless of behavior: air a_V< CEA, litter aV< CEA (T_q= 293 kelvins (K), a_Vq= 0.8, T_r= 293 K, a_Vr= 0.8), where aV is water vapor activity; CEA is the critical equilibrium activity; T_q and a_Vq are the temperature and water vapor activity above the leaf litter, respectively; T_rand a_Vr are the temperature and water vapor activity below the leaf litter, respectively; p_q(t) is the proportion of day t spent questing. The strategy is constant for all days except t. (B) p_q(t) heatmap when ticks gain water regardless of behavior: air a_V> CEA, litter a_V> CEA (T_q = 293 K, a_Vq = 0.9, T_r = 293 K, a_Vr = 0.9). Day 15 is shown.

3.2.3. If ticks gain water regardless of behavior, water reserves are irrelevant

When air a_V > CEA, meaning the tick can replenish water reserves by questing, a tick’s current water reserves cease to affect optimal strategy. In the optimal strategy heatmap, only the lipid-limited area remains (Fig. 5B). As a consequence, ticks that can gain water while questing quest more than those that cannot for nearly all state combinations (Supplementary Fig. S5A). Similarly, when questing does lead to water loss, less desiccating environments lead to more questing time over the full season (although there are nevertheless many individual state combinations at which ticks subjected to more desiccating environments choose higher p_q(t) (Supplementary Fig. S5B)).

3.3. “Island” ticks are fitter than “mainland” ticks in their respective home ranges, but less fit under a simulated inland expansion

Drawing an analogy with the hypothesized inland expansion of historically coastal ticks, we compared model output from “island” and “mainland” environments. Climate data were derived from averaged climate measurements at field sites on Block Island, Rhode Island (USA) and North Branford, Connecticut (USA), respectively, from June-September 2014. We used HOBO® weather stations (Onset Computer Corporation, Bourne, Massachusetts, USA) to measure air temperature and humidity and iButton® loggers (Maxim Integrated, San Jose, California, USA) to measure temperature and humidity in the leaf litter (M. Diuk-Wasser, unpublished data). The island scenario is notable for an air water vapor activity above the CEA.

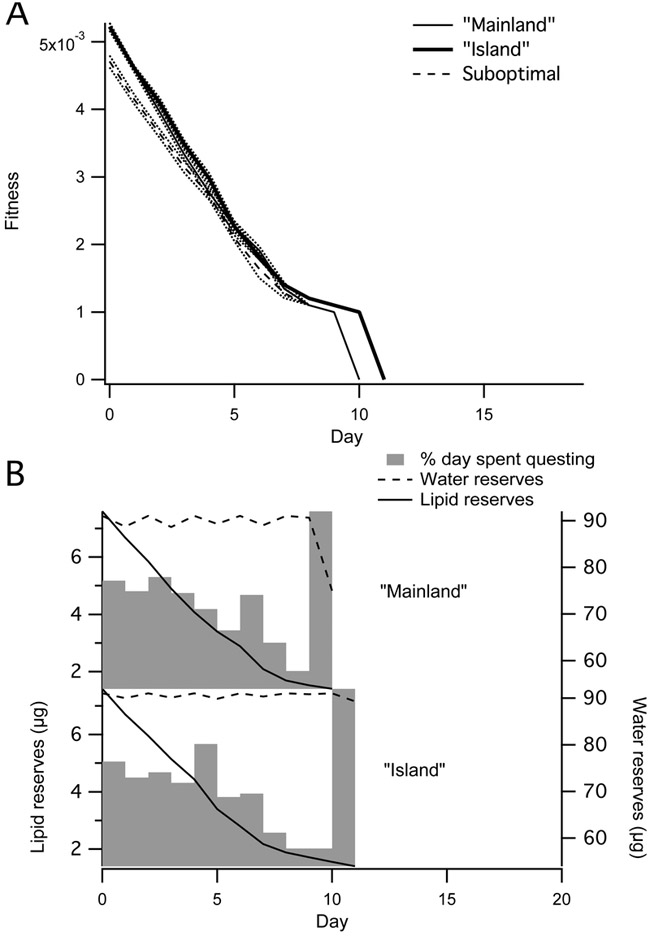
Given optimal behavior, the fitness for a tick starting with full lipid and water reserves is overall higher in the island scenario; fitness values at both sites remain similar until the end of the simulation, at which point ticks on the mainland exhaust lipid reserves one day prior to those on the island (Fig. 6A).

Fig. 6.

Comparison of “Island,” “Mainland,” and suboptimal (“Island” to “Mainland”) climate scenarios. The dynamic programming equation was run stochastically 10 times and averaged over a 20 day season. Plots represent a forward simulation along this averaged result, with deterministic tick energy and water state variable equations. Each individual nymph trajectory ends when a tick has reached a lipid or water boundary condition. (A) Plot of fitness scores over season (starting parameters x = 7.6 μg, w = 91 μg, where x refers to lipid reserves and w to water reserves). (Note that the “Mainland” trace is obscured by the suboptimal trace at points.) (B) Percentage of time spent questing (gray bars), lipid reserves (solid lines), and water reserves (dashed lines) by day for a tick under each scenario (starting parameters x = 7.6 μg, w = 60 μg). Bars representing the percentage of the day spent questing are scaled so that 0% aligns with x_min and w_min and 100% is even with x_start and w_max, where x_min and x_start are the tick’s minimum and starting lipid reserves, respectively, and w_min and w_max are the tick’s minimum and maximum water reserves.

To simulate a tick moving from an island to a mainland environment, we subjected an island-adapted tick to a mainland climate using equation 8. Fitness values for the suboptimally behaving tick (again, starting with full lipid and water reserves) remained below those of the island tick at most points during the season. Fitness values remained below those of the mainland tick for the beginning of the season, but then became indistinguishable (Fig. 6A).

3.4. Tick populations uncertain of their local climate optimally adopt a mix of strategies

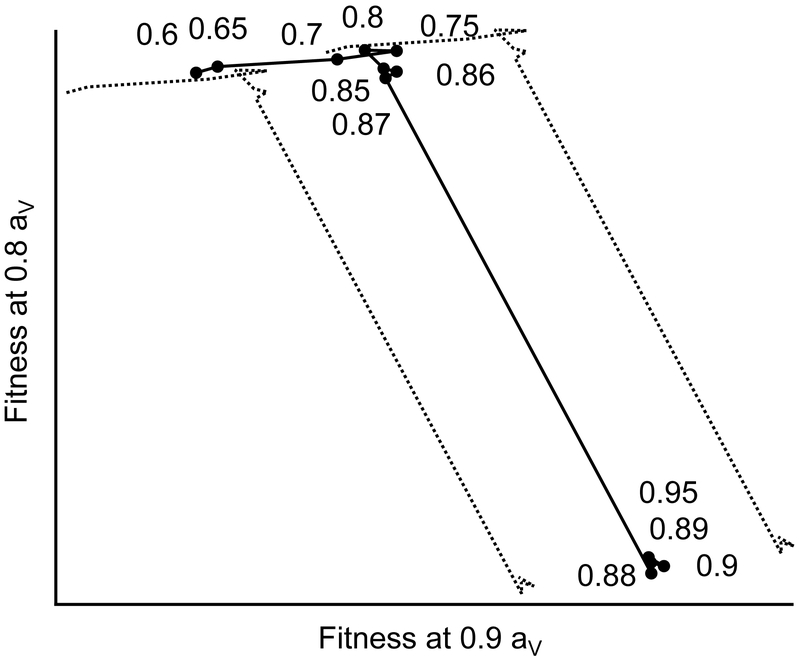
We evaluate the questing fitness set on axes defined by fitness under 0.8 air a_V and 0.9 air a_V scenarios (air temperature is kept constant at 293 K to simplify analysis; litter conditions are T=293 K, a_V=0.9). The phenotype set consist of ticks adapted to various other air water vapor activities, with all other climate variables held constant. The fitness index is calculated as the sum of the average fitness scores (over 10 runs) for all combinations of state variables and day of season.

We find that “intermediate” phenotypes (questing strategies optimally adapted to 0.8 < a_V< 0.9) generate fitness scores that do not differ significantly from those of the “specialized” phenotype (questing strategies optimally adapted to either a_V = 0.8 or a_V = 0.9) that lies on the same side of the CEA. This invisibility of “intermediate” phenotypes to selection makes the fitness set between CEA-spanning climates de facto concave (Fig. 7).

Fig. 7.

Tick fitness set across the critical equilibrium activity (CEA). Ticks optimally adapted to a given air a_V (water vapor activity, indicated by point labels) are subjected to air a_V conditions of either 0.8 or 0.9. Air and litter temperature are held constant at 293 kelvins (K); litter a_V is held at 0.9. Each point represents the fitness of a single tick that is optimally adapted to the air a_V indicated by the nearest label. The horizontal position of each point represents the summed fitnesses of all state combinations over an entire season for the given tick at air a_V 0.9. The vertical position represents the summed fitnesses of that tick at air a_V 0.8. Fitness scores are the average of 10 stochastic runs. Dotted lines represent summed horizontal and vertical 95% confidence intervals.

4. Discussion

We present what we believe to be the first model of tick questing behavior to make use of either dynamic state variable techniques or biophysical parameters. The approach theoretically allows us to predict changes in tick behavior and fitness in response to changing environmental conditions, as in the case of the posited historical inland invasion of ticks from coastal and island refugia.

We found that the optimal predicted questing strategy changed non-linearly as leaf litter and air water vapor activity crossed the tick’s critical equilibrium activity (CEA) – a physiological threshold below which the tick was unable to maintain a steady state water balance. Questing strategy falls into three qualitative climate categories: air a_V< CEA < litter a_V; air a_V< CEA > litter a_V; and air a_V> CEA < litter a_V. Ticks questing in air more humid than the CEA threshold enjoy a fitness advantage relative to ticks in drier environments. These humid-specialized ticks are, however, at a disadvantage if they continue to apply this strategy (i.e., fail to adapt) after moving to a drier region. In an uncertain climate that varies across the CEA, questing behaviors intermediate to the dry- and humid-specialized strategies do not confer a fitness advantage. Ticks would therefore be expected to produce a mix of specialized behavioral phenotypes among their offspring.

Although there is debate about whether parasites are under evolutionary pressure to behave optimally (Thomas et al., 2002), tick host-seeking behavior is at the very least a plausible target for adaptive evolution. Questing phenology affects tick survival, and significant variation in the intrinsic propensity to quest is apparently present even within regional populations (Van Es et al., 1999). Most convincingly, common garden experiments have demonstrated heritable variations in questing propensity between ticks from regions with differing climates (Gilbert et al., 2014; Arsnoe et al., 2015). It could be argued that such differences do not indicate optimal or even near optimal adaptation to local environments, not least because the ability to meaningfully adapt to a local climate depends on the degree of climate variability both within and across seasons. While this criticism is reasonable, our approach is primarily intended as a mathematical expression of a classical model of tick behavior that better defines the potential fitness attributable to strategic host-seeking.

We avoid using more complex host population dynamics in our model, as it is debatable whether tick populations anticipate variations in host abundance over the course of the season in a meaningful way. Models of host-finding success and its relation to host populations have been thoroughly investigated elsewhere (Lou and Wu, 2014). We do, however, observe a reduction in questing when the probability of finding a host in the leaf litter is greater than 0. This behavior is reminiscent of that of southern forms of I. scapularis. Ticks from the Carolinas (USA), which are thought to parasitize lizards under the leaf litter, are significantly less likely to host-seek above the leaf litter than northern ticks that parasitize bird and mammal hosts (Arsnoe et al., 2015).

Per Lees’ paradigm, hard tick questing should decrease under desiccating conditions and vice versa (Lees, 1946). In a laboratory setting, water vapor activity a_V and saturation deficit (a measure of desiccation risk that is a decreasing function of a_V) have, accordingly, been shown to be positively correlated with questing height (Randolph and Storey, 1999; Vail and Smith, 2002) and duration (Perret et al., 2003) among Ixodes congeners. Field studies of Ixodes spp. do not always bear out this finding; the relationship between a_V or saturation deficit and the proportion of nymph population that is questing has been found to be positive (Perret et al., 2004) and negative (Rynkiewicz and Clay, 2014).

Field studies seem similarly divided on whether there is a positive and a negative correlation between temperature and the proportion of questing Ixodes nymphs. This inconsistency may, however, reflect a unimodal relationship between temperature and questing behavior. Under experimental conditions, the time ticks spend in questing posture has been shown to peak at 298 K (Vail and Smith, 2002). Field data are broadly consistent with this finding; at least one study that found positive correlations between temperature and the proportion of questing nymphs was conducted under conditions consistently cooler than ~298 K (Rynkiewicz and Clay, 2014), while two studies that found negative correlations between temperature and either the proportion of questing nymphs or the deviation of questing nymph density from expected density based on day of season were conducted at warmer temperatures (Vail and Smith, 1998; Perret et al., 2004).

In our model, we found that less desiccating conditions were typically more favorable for questing. There are, however, many state combinations that show increased questing under more desiccating conditions, in part because such conditions effectively shorten the questing season (Supplementary Fig. S5). Increased tick questing under apparently desiccating conditions may also be observed in our model when leaf litter water vapor activity has fallen below the CEA.

More generally, our biophysical model of tick water loss and gain – based primarily on the general formulation of arthropod water balance by O’Donnell and Machin (1988) - implies that water use and related behaviors change non-linearly over certain thresholds, including the CEA, PT and CCTT. Due to this non-linearity, relatively large behavioral differences may exist between ticks in locations with relatively small climatic differences, as long as the gradient between the two crosses a physiological threshold. There is some field evidence of such an effect – the number of days in a season with an a_V below 0.82 appears to have a negative relationship with overall nymphal densities (Berger et al., 2014).

Our model also provides predictions about the effect of the tick’s internal state on its behavior, a concept explored conceptually as early as 1934 by Uexküll (2010) and felt by Lees to outweigh the importance of environmental factors (Lees, 1969). For practical reasons, there is far less empirical data on the relationships between tick internal state and host seeking. Experiments in Dermacentor (McEnroe and McEnroe, 1973) and Rhipicephalus (Punyua et al., 1985) suggest that increased water reserves are positively correlated with questing activity, consistent with both the Lees model and our model output.

Our finding that ticks with critically low lipid reserves increase their questing is consistent with experimental data showing that lipid-depleted ticks walk more than ticks with relatively full lipid reserves (Herrmann and Gern, 2012), although our model also predicts that high-lipid ticks will quest before moderately low-lipid ticks. The burst of end-of-season questing produced by the model has not been reported in the field to our knowledge, although the finding may be unlikely in a population of ticks that is heterogeneous with respect to lipid reserves and molting times. We also do not account for the subpopulation of unsuccessful nymphs that have been observed to survive the winter and host-seek for a second season – behavior that would change the reward function of our model (Yuval and Spielman, 1990).

Extrapolating from these basic results to the simulated inland migration of ticks from island refugia, we find that there are fitness consequences to the patterns described above. Regardless of whether ticks exposed to our “mainland” conditions behave optimally or suboptimally (i.e. retain a “coastal” questing strategy), they experience lower host-finding success in our model relative to their “island” relatives. While the difference consists of a single day of questing in our analysis – an advantage that is unlikely to be biologically meaningful – it is difficult to know if the absolute magnitude of this difference should be taken at face value.

Our results are also predicated on several other important assumptions. In our analysis, regional tick subpopulations vary only in behavior. Ticks may, however, vary physiologically in lipid or water usage, as is suggested by limited evidence that ticks from different regions enjoy different survivorships (Ginsberg et al., 2014). Our results are limited to nymphs, while field tick abundances and phenology are dependent on the interacting demography and behavior of the three life stages. Finally, we only consider climatic differences between island and mainland environments and do not consider differences in host populations between the two regions.

Upon further analysis of the island-mainland fitness differential using fitness sets, we find that a tick’s optimal reproductive strategy in a climate that varies unpredictably across the CEA is to generate a mixture of offspring specialized to either the drier or more humid scenario (Levins, 1968). While the calculation method we use is crude, the results are intuitive given the presence of the known physiological threshold. These theoretical findings might be corroborated by the presence of greater variability in intrinsic questing propensity among tick populations exposed to unpredictable conditions (e.g.: tick populations that parasitize hosts that migrate between island/coastal and mainland environments), compared with tick populations that experience invariant climates.

Beyond the inherent abstraction and underlying assumptions of the dynamic state variable approach, the realism of our model is limited in part by the accuracy of our physiological parameters and mechanistic assumptions. The lipid usage formulas we use here are rough approximations, and our decision to treat water uptake as passive and independent of energy state, while compatible with the water usage literature cited in the section 2, is simplistic. A model that includes both passive and active (energy-requiring) water vapor absorption would result in a more complex interplay between lipid reserves, water reserves, and questing strategy.

The current version of the model also omits other potential influences on tick behavior, some of which could be incorporated into alternate dynamic state variable approaches. Most notably, photoperiod cues are known to affect questing behavior. In I. ricinus, for instance, behavioral diapause in nymphs and larvae is induced by short days, nymphal development proceeds after a transition from short to long days, and long days induce increased activity (Belozerov, 1982). In our model, photoperiod as an independent driver of tick behavior is roughly equivalent to the tick’s knowledge of day of season, although the analogy is imperfect (Randolph, 2004). It would be possible to treat the tick’s knowledge of the day as imprecise (a more reasonable assumption than ours, which results in an artifactual 100% questing rate on the final day of the season), or include photoperiod as a separate environmental variable that directly affects host-seeking propensity. Because we use a day-long time step, we also do not take into account diurnal variation in environmental variables.

The theoretical approach we describe here can be used to guide investigations of geographic gradients of tick behavior, common garden arena experiments, and experimental manipulations of the tick internal state. In particular, we intend to compare field data on host-finding success (or other fitness measure) along a coast-inland gradient with the above calculations of fitness differences between optimally- and suboptimally-behaved ticks in coastal and mainland climates. In order to do so, we may incorporate historic climate and host availability time series into future versions of the model in the hope of generating actual phenological predictions, and extend the dynamic programming approach to the tick’s full life cycle. These more realistic outputs may serve as a basis for further modeling of transmission of Lyme disease and other pathogens in response to changing climates and vector migration. As they stand, the current model’s predictions may parameterize timing and host-finding success in other epidemiological models.

Supplementary Material

1

Supplementary Fig. S1. Ixodes scapularis nymph permeability as a function of temperature, corrected for saturation deficit (Beament, 1959). Separate linear regressions for temperatures below and above 306.4 kelvins (K) are shown, with associated R² (coefficient of determination).

2

Supplementary Fig. S2. Ixodes scapularis LT₅₀ (median lethal time) as a function of air a_V (water vapor activity). Three data points below pump threshold fit to the transpiration equation with R²=0.93 (Yoder and Spielman, 1992; Stafford III, 1994). Note the fourth data point in the upper right.

3

Supplementary Fig. S3. Net hourly change in tick water reserves as a function of temperature. Change in water reserves was evaluated at water reserve=72 μg over various a_V (water vapor activity) ranges, taking the critical cuticle transition temperature (CCTT) of 306.4 kelvins (K) into account. (A) Below the pump threshold (PT; a_V=0.75), net hourly water change always becomes more negative (i.e., ticks lose water more quickly or gain water more slowly) as temperature increases. Note split vertical axis. (B) Between the PT and critical equilibrium activity (CEA: a_V=0.8), water change becomes more positive (i.e., ticks lose water more slowly or gain water more quickly) with temperature below the CCTT and becomes more negative with temperature above it. Note the split vertical axis. (C) Above the CEA (a_V=0.9), water change always becomes more positive with temperature.

4

Supplementary Fig. S4. Lipid edge slope. Model output generated using a dynamic programming equation with deterministic tick lipid and water use functions under varying air water vapor activities, showing that the slope of the edge of the lipid-limited area is dependent on both lipid cost and water cost. (For all runs, other climate variables were T_q=293 kelvins (K), T_r=293 K, a_Vr=0.9, where a_V is water vapor activity and T_q and T_r are the temperature above and below the leaf litter, respectively). (A) Lipid edge slope as a function of air water vapor activity. (B) Lipid edge slope as a function of questing lipid use rate, a_Vq=0.8. (C) Illustration of slope measurement. Image corresponds to the questing propensity matrices shown in Figs. 4 and 5 in the main text, evaluated on day 10 of a 20 day season: horizontal axis represents lipid reserves in μg, vertical axis represents water reserves in μg, and the shade of each cell represents the percentage of a day spent questing, with lighter shades representing higher proportions. Bands of alternating shades represent artifactual “gridding” (Houston and McNamara, 1999). The superimposed lipid edge slope (white angle in upper left) is measured relative to the upper horizontal axis of the image. For A, the slope is defined by a line drawn from the upper left corner of the low questing propensity (black) column at x=2.2 μg to the upper left corner of the low questing propensity column at x=3.1 μg (where x refers to lipid reserves). For B, the slope is defined by a line drawn between the upper left corners of the first and last coherent low questing propensity columns.

5

Supplementary Fig. S5. Representative model output showing differences in tick questing propensity due to desiccation while questing. (A) Each grid represents a matrix of all possible state combinations on a given day (where t is the final day of the season), showing whether ticks subject to a non-desiccating questing climate (T_q=293 kelvins (K), a_Vq = 0.9, T_r=293 K, a_Vr=0.9) quest less than ticks subject to a desiccating questing climate (T_q=20C, a_Vq = 0.8, T_r=20C, a_Vr=0.9) at the given state combination (where a_V is water vapor activity; T_q and a_Vq are the temperature and water vapor activity above the leaf litter, respectively; T_r and a_Vr are the temperature and water vapor activity below the leaf litter, respectively). Values are true (white) or false (black). (B) The same analysis as in A, showing whether ticks subject to a less desiccating questing climate (T_q=293 K, a_Vq = 0.8, T_r=293 K, a_Vr=0.9) quest less than those subject to a more desiccating questing climate (T_q=293 K, a_Vq = 0.7, T_r=293 K, a_Vr=0.9).

Table 2.

Definitions of constants used in the dynamic state variable model

Constant	Definition
N	Nymphal stage
A	Adult stage
xmin	Minimum lipid reserves (μg)
xstart	Starting lipid reserves (μg)
wmin	Minimum water reserves (μg)
wmax	Maximum water reserves (μg)
cr	Daily energetic cost of resting (μg/day)
cq	Daily energetic cost of questing (μg/day)
t	Final day of season
kT	Transpiration water loss constant (μg/[hr*K2])
An, Bn	Water gain constants (μg/[hr*K], μg/hr)
aw	Tick body water activity (RH/100)
CEA	Critical equilibrium activity (RH/100)
PT	Pump threshold (RH/100)
CCTT	Critical cuticle transition temperature (K)

Highlights.

• Optimal Ixodes scapularis questing strategies change depending on climate

• Ticks in humid environments are fitter than those in drier regions

• Ticks suffer reduced fitness when moved to drier climates than they are adapted to

• In uncertain climate scenarios, tick populations optimally adopt a mix of behaviors