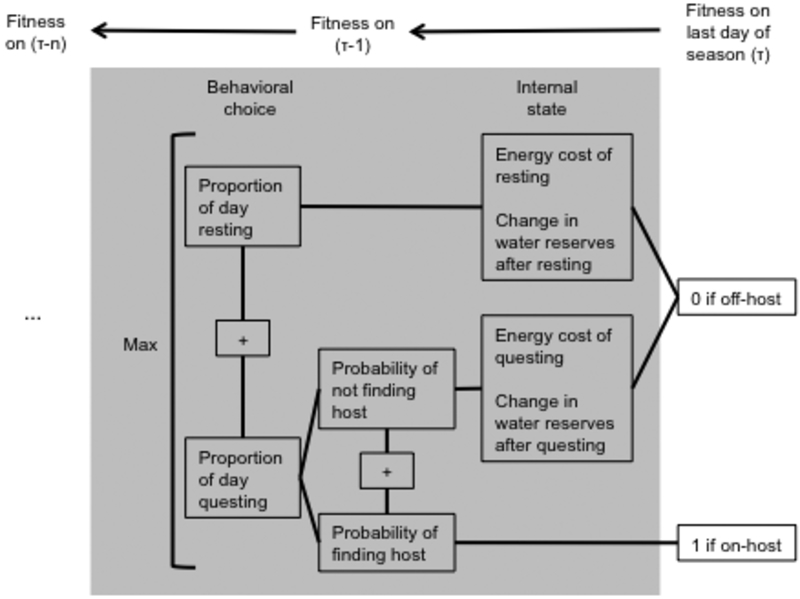
Fig. 1.
Model schematic. The dynamic programming equation defines a fitness reward for each tick life stage at the end of the season: 1 for on-host ticks, 0 for off-host. Fitness (defined as the overall probability of finding a host by the final day of the season t) on the penultimate day of the season is defined by calculating the probability of receiving each of these “rewards” under various values of pq(t-1) (proportion of day t-1 spent questing) and then selecting the highest value. For a given pq(t-1), a tick’s probability of finding a host is pq(t-1)hq(t-1) (where hq(t) is the probability of finding a host on day t), while a tick’s probability of not finding a host is pq(t-1)(1-hq(t-1)). (These expressions assume the probability of finding a host while resting is 0). The total payoff associated with behavioral choice pq(t-1) is the sum 1*pq(t-1)hq(t-1)+ 0*pq(t-1)*(1-hq(t-1)). The tick should choose pq(t) to maximize the sum of these payoffs, meaning in this case that the tick will allocate all of its time to questing (pq(t-1)=1). Fitness on day t-1 is therefore hq(t-1). As time moves backwards, fitness on day t is dependent on the fitness on day t+1 of a tick with the internal state variables that are the result of the tick’s choices – because if a tick does not find a host, its internal state variables x and w (energy and water, respectively) change according to how much time it spent on each activity. Fitness is calculated (and maximized) for every combination of state variables on every day until the first day of the season.