Long-term recording reliability of liquid crystal polymer μECoG arrays

Abstract

Objective.

The clinical use of microsignals recorded over broad cortical regions is largely limited by the chronic reliability of the implanted interfaces.

Approach.

We evaluated the chronic reliability of novel 61-channel micro-electrocorticographic (μECoG) arrays in rats chronically implanted for over one year and using accelerated aging. Devices were encapsulated with polyimide (PI) or liquid crystal polymer (LCP), and fabricated using commercial manufacturing processes. In vitro failure modes and predicted lifetimes were determined from accelerated soak testing. Successful designs were implanted epidurally over the rodent auditory cortex. Trends in baseline signal level, evoked responses and decoding performance were reported for over one year of implantation.

Main results.

Devices fabricated with LCP consistently had longer in vitro lifetimes than PI encapsulation. Our accelerated aging results predicted device integrity beyond 3.4 years. Five implanted arrays showed stable performance over the entire implantation period (247–435 days). Our regression analysis showed that impedance predicted signal quality and information content only in the first 31 days of recordings and had little predictive value in the chronic phase (> 31 days). In the chronic phase, site impedances slightly decreased yet decoding performance became statistically uncorrelated with impedance. We also employed an improved statistical model of spatial variation to measure sensitivity to locally varying fields, which is typically concealed in standard signal power calculations.

Significance.

These findings show that μECoG arrays can reliably perform in chronic applications in vivo for over one year, which facilitates the development of a high-density, clinically viable interface.

1. Introduction

Neural interfaces are widely used for chronic disease management, sensory restoration, and motor rehabilitation. Several devices that interface with the cerebral cortex use either penetrating, epidural, subdural, or scalp electrode arrays to monitor or stimulate the brain for therapeutic benefit. The central challenge with implantable interfaces is the acquisition of reliable, high-fidelity neural recordings over extended periods of time, and ideally for the lifetime of the patient [1]. Intracortical microelectrode arrays have shown stability for multiple years in non-human primates [2]–[7] and humans [8], yet are restricted to small cortical areas, which limits the capacity for the spatial integration underlying higher-level cortical processing in health and disease [9]–[16].

Efforts towards achieving greater neural interface reliability over large cortical regions have motivated use of electrocorticography (ECoG) interfaces for advanced therapies, including long-term ECoG implants in humans for seizure monitoring (up to three years) [17], and responsive cortical stimulation for seizure arrest (more than two years [18], [19]). Interestingly, in the same trial, the impedance of subdural electrodes increased slightly in the first 12 weeks after implant, but then remained stable for up to four years observed so far [20]. Based on the early success of macro-scale ECoG recordings in implantable therapeutic devices, the use of microscale signals could offer improved outcomes for seizure diagnostics. The advantages of microscale interfaces include higher resolution [21]–[24], improved biomarker detection rate [25], and sensitivity to putative precursors that predict clinical seizure events [25], [26]. For instance, microscale electrode arrays can better detect high-frequency oscillations [24], [27]–[29] and microseizures [26], [30], [31] which are either not observed on existing macroelectrodes or poorly sampled. These are known biomarkers of epileptic activity but not yet used for diagnosis.

The use of microsignals to better inform seizure diagnostics, and more broadly, in research on cognition [32] and brain-computer interfaces [10], [15], [33]–[35], motivated the growing adoption of micro-ECoG (μECoG) electrode arrays. This emerging class of devices provides a high-resolution neural interface that is less invasive to cortical tissue while covering larger areas compared to penetrating microelectrode arrays without compromising the information content of the acquired signal [9]. While there is mounting evidence of the utility of microscale neuro-dynamics for improved clinical diagnostics, these devices largely remain in the research domain as their chronic reliability is proven across many cortical applications. To date, variants of μECoG arrays have been implanted for periods of weeks to years in rats [36]–[41], non-human primates [42]–[46], and humans undergoing epilepsy monitoring [34], [47].

The devices in the above μECoG studies were fabricated with biocompatible materials, including insulation with either medical-grade silicone, parylene, or PI. However, there are known limitations in using these materials for stable, high-density electrode geometries, which leads to a trade-off between electrode resolution and device reliability. Namely, silicone-encapsulated devices have been proven to last up to 25 years during chronic implants [48], yet in array stack-ups, silicone can only achieve lower electrode densities due to its fabrication with machined metal contacts, individual wiring, and manually welded interconnects [49]. Emerging designs utilizing patterned foils embedded within silicone stacks enable higher densities with precision at ~50 μm, compared to machined designed with ~500 μm resolution [50]. Thin-film designs can support microfabrication methods for batch processing of high density electrode arrays but may suffer from delamination when chronically implanted [48]–[50].

To investigate μECoG reliability, we leveraged industrial manufacturing processes as a low-cost solution for rapid prototyping multiple array designs. The flexible printed circuit board (PCB) methods we utilized allowed wires as fine as 25 μm wide spaced 25 μm apart. Our preliminary in vitro assessment of these devices revealed that polyimide (PI) and liquid crystal polymer (LCP) devices showed early promise for long-term stability with the potential for future clinical use [51]. PI is widely used in research electrode arrays as well as in the Second-Sight Argus II and III retinal prostheses [52], [53]. LCP is an FDA-approved material (with a USP XXII, Class VI bio-compatibility rating), and is considered safe for use within the body [54]–[58]. The LCP used in this study has passed all major ISO 10993 biocompatibility test panels [59], [60].

The established biocompatibility and the interest in high-density spatial sampling in a scalable cortical interface support the potential for μECoG in chronic neural therapies. This emerging direction invites an added layer to the current discussion of metrics for long-term electrode reliability. In previous materials characterizations of implantable arrays [5], [61]–[66], often abiotic factors are studied independently of biotic mechanisms [67], [68]. This point is highlighted by the DARPA initiative on Biocompatibility of Advanced Materials for Brain Interfaces (BAMBI) [69], [70]. Its focus was to develop a test bed to evaluate the multi-faceted challenge of chronic electrode stability. These methods were deployed to characterize the precise evolution of interfacial processes and chronic neural recording for a number of neural platforms, including microwire arrays [71]–[73]. However, reliability metrics based on spiking rates are inappropriate for most μECoG arrays, and tissue health and site impedances have not yet been correlated with the effectiveness of μECoG devices to capture high-resolution, spatially varying neural dynamics. New measures, such as sensory decoding and spatial field analysis, are needed as markers of long-term reliability when recording a spatially diverse signal.

Here we further examined the interplay between biotic and abiotic mechanisms and offer a reliability analysis relevant to high-density μECoG devices for chronic implantation. First, we report standard measures of electrode health, including impedance and background signal characteristics. Second, we report stimulus-evoked signal-to-noise ratios (SNR) and stimulus decoding performance. High-density μECoG recordings are spatially correlated, but not purely redundant samples of cortical potential. We employ a model of spatial variation (adapted from [74]) that reveals the amplitude of field and noise signal components, and longitudinally tracks the length-scale of spatial covariance. Finally, a cross-validated regression of signal quality against impedance yields insight into the predictive value of electrode impedance on evoked response metrics. Our regression analysis further showed that impedance predicted signal quality and information content in the first 31 days of recordings but was not a consistent covariate at later timepoints. In the chronic phase, site impedances gradually decreased yet decoding performance remained constant. These findings support the conclusion that μECoG arrays can reliably perform in chronic neural applications in vivo for over one year.

2. Methods

2.1. Electrode fabrication

Our prior work with low cost arrays fabricated using thin-film methods showed stable performance for ~30 days of implantation [74]. However, we aimed to improve the chronic reliability of this design by using a two-layer stack-up employing only noble metals. The specific comparison between PI and LCP is the result of our initial screening efforts for materials with known biocompatibility for future clinical possibilities with thin-film methods [51]. Both array stack-ups used two-layer pure gold (i.e., no copper or nickel) processes with 61 contacts laid out in an 8×8 grid with approximately 200 μm diameter contacts spaced approximately 420 μm center-to-center (figure 1). Instead of having the electrode openings laser-cut or etched, we used micro-vias to connect the inner metal layer forming the electrode interconnects to the surface metal layer. The surface layer contained only the exposed electrode pads and the zero-insertion force (ZIF) connector contacts. The inner layer contained all the interconnections. The PI array was fabricated by Averatek (Santa Clara, CA; figure 1(b)) using Kapton 50HN as the PCB core with solution-processed PI-2611 as the coverlay.

Figure 1.

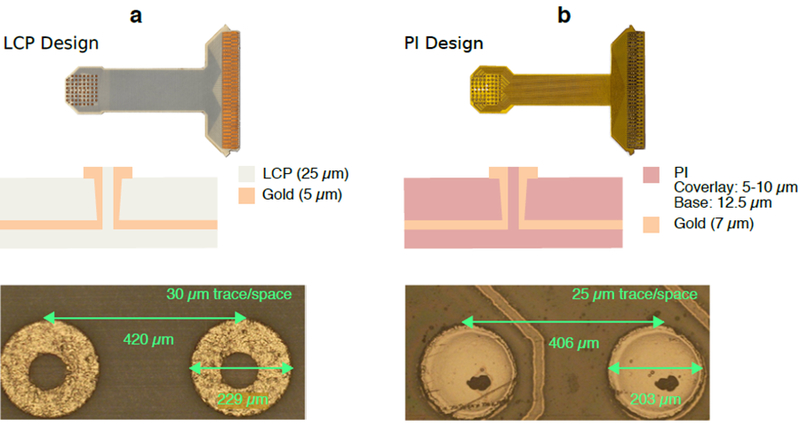
Stack-ups of μECoG array designs fabricated from (a) liquid crystal polymer (LCP), and (b) polyimide (PI). Both arrays were fabricated using gold for contacts and interconnects. The LCP array (a) was fabricated using Ultralam 3850/3908 as the PCB core and coverlay, respectively. The PI array (b) was fabricated using Kapton 50HN as the PCB core, and solution-processed PI-2611 as the coverlay. Electrode geometry and inter-electrode spacing were roughly matched, shown in the microscopy images. Micro-vias are shown in the center of each contact to connect to the embedded traces.

The μECoG arrays used for implantation were fabricated with LCP and manufactured by Dyconex (Bassersdorf, Switzerland; figure 1(a)) using Ultralam 3850 HT (Rogers Corporation) as the PCB core with Ultralam 3908 (Rogers Corporation) as the coverlay. The process stages are shown in supplemental figure 1. Once copper was etched away from the Ultralam 3850 HT layer, vias were laser drilled into the LCP sheet and a Palladium (Pd) seed layer was applied to both sides of the sheet to pattern the geometry of the sensing pads (outer layer) and the interconnect traces (inner layer). Gold was then electroplated from the Pd seeds to a thickness of approximately 5 μm, to develop electrode pads and interconnect traces. The Ultralam 3908 encapsulation sheet was then laminated to the trace side of the array using a uniaxial press with a prescribed temperature-pressure profile over time that allowed the two LCP layers to melt and then bond during the press cycle. In this stage, LCP flowed into the micro-via gap to produce continuity of the encapsulation. Finally, the outlines of the individual arrays were laser cut from the full PCB sheet [75].

2.2. Accelerated aging characterization

2.2.1. Testing set-up

Our accelerated aging methods were previously published in [51]. Briefly, each device was immersed in phosphate buffered saline (PBS) with a pH of 7.4 (Quality Biological, MD), and its test tube was sealed with a custom cap and heat-resistant silicone (500° RTV high heat silicone sealant, Rutland, IL). Test chambers were stored at an elevated temperature (60°C) in an incubator (ReptiPro 6000, ReptiPro, FL), resulting in a five-fold acceleration over body temperature (37°C) [76]. The electrodes were connected in a two-terminal configuration against a gold-coated reference wire. Measurements at 1 kHz were collected weekly using a 1.4 nA RMS AC test current (nanoZ multielectrode impedance meter, White Matter LLC, Mercer Island, WA).

2.2.2. In vitro impedance analysis

Devices were first screened for connectivity, as some μECoG arrays did not have 100% fabrication yield. In our preliminary accelerated aging study across a broader range of thin-film encapsulants [51] combined with our previously reported in vivo recording performance using devices fabricated with commercial cleanrooms [74], the impedance range between 1 kΩ to 1 MΩ (at 1 kHz) captured the working range for system connectivity. Sites having an initial impedance magnitude within the 1 kΩ - 1 MΩ range were subsequently tracked throughout the experiment. Electrode failure was determined by impedance measurements outside of the screening range on two successive days. We defined array failure as the point where the electrode yield dropped below 50% of the initial working sites.

2.3. Surgical procedure

All animal procedures were performed in accordance with National Institutes of Health standards and were conducted under a protocol approved by the Duke University Institutional Animal Care and Use Committee. Five female Sprague-Dawley rats weighing 225–275 g were anesthetized using isoflurane (induction 3–5% at 1–3 L/min and maintenance 0.5–3% at 0.6–1.0 L/min). The surgical area was shaved, and properly sterilized according to standard sterile procedures. The head was secured in a custom head-holder orbital clamp with nose cone attachment for continuous gas delivery while leaving the ears unobstructed. Each animal received subcutaneous injections of buprenorphine SR-LAB (1.2 mg/kg; ZooPharma) for pain management and dexamethasone (0.3 mg/kg) to minimize cerebral swelling. Bupivocaine 0.25% (1 mg/kg) was administered subcutaneously local to the incision site. All surgeries in this study were performed by a single surgeon to minimize variations in the surgical implantation procedure. A longitudinal incision was made along the midline and periosteal membranes removed to expose the skull. Five bone screws (00–96 × 3/32; Plastics One) were inserted into the skull around the point of entry using a hand-held micro-drill and 0.8 mm drill bit (Roboz Surgical Store, Gaithersburg, MD). The right temporalis muscle was reflected, and a 5×5 mm² craniotomy was performed over right auditory cortex. A sterilized electrode array (figure 2(a)) was placed epidurally over the core auditory cortex using vascular landmarks. Arrays selected for implantation had 95–100% yields with absolute values between approximately 30–60 kΩ at 1 kHz. Placement was optimized with intraoperative recordings of electrode impedance and auditory stimuli described below. Once array placement was confirmed, the craniotomy was covered with an absorbable gelatin sponge (GELFOAM) and secured with dental cement (C & B Metabond Quick! Luting Cement). Silver grounding wires (0.25 mm diameter; Sigma Aldrich) on the headstage were wrapped around the five bone screws to be used as an electrical recording reference and secured with high-grade dental cement (C & B Metabond Quick! Luting Cement). The remaining area of the electrode pedestal was securely anchored to the skull using a lower grade dental acrylic (LANG Jet Denture Repair). The surgical site was flushed with a povidone-iodine (Betadine) solution and the incision points were sutured. Postoperative antibiotics (Baytril 5 mg/kg) and dexamethasone were administered twice daily for 3-days post-op for full recovery. Initial electrophysiological recordings were made 7 days following implantation.

Figure 2.

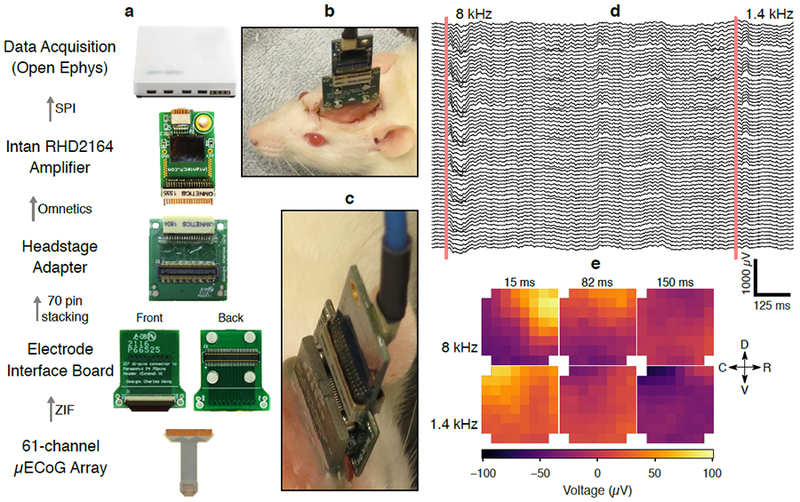
Recording system for μECoG data collection. (a) The 61-channel LCP electrode was implanted over auditory cortex of the right hemisphere. The electrode was connected to the electrode interface board (EIB), which was also permanently implanted on the skull of the animal. The EIB contained a 70-pin board stacking connector (Panasonic P4 series) and retention magnets. The magnets facilitated self-alignment of the board stacking connector and provided additional retention force to prevent the headstage from becoming disconnected during recordings. During recordings, an Intan 64-channel digital amplifier (RHD2164) was connected to the EIB via a board-stacking to Nano Strip (Omnetics Connector Corp) adapter board (also fitted with retention magnets). Electrode potentials were digitized at 20 kS/s using the Open Ephys data acquisition hardware and software. (b) Image of an Intan RHD2164 amplifier and adapter PCB connected to an implanted recording device in rat. (c) Detailed image of connecting parts. (d) Raw μECoG potentials from an awake and freely moving rat during two tone-presentation trials (lowpass filtered at 800 Hz for display). (e) Snapshots of electrode potential arranged in the geometry of the 8×8 electrode grid show differential propagation patterns of tone-evoked responses depending on the frequency of the tone. All implants were roughly aligned with the anatomical coordinates (dorsoventral and rostrocaudal axes) drawn in (e).

2.4. In vivo recordings

A head-mounted PCB connected the electrode ZIF connector to a male high-density board-stacking connector (Panasonic P4 series, Panasonic Corporation, Kadoma, Osaka, Japan). For each recording session, a female P4-to-Omnetics adapter and a pre-attached Intan RHD 2164 64-channel amplifier board was attached to the animal’s head. Magnets in the head-mounted PCB and adapter PCB provided self-alignment to make connection to the animal fast and easy. Digital data from the Intan amplifier were transferred via a thin and flexible SPI tether, and logged with the Open Ephys system at 20 kS/s [77] (figure 2(a)). Multisite impedance at 1 kHz was also collected through this system.

All recording sessions were carried out in a sound-attenuated chamber. Acoustic stimuli were generated with custom MATLAB code through an NI 6289 DAC card, and delivered through a free-field speaker (CR3, Mackie) calibrated to have a flat output over the frequency range used. Responses to tone pips of 13 frequencies (0.5 – 32 kHz, 0.5 octave spacing, 50 ms in duration, 2 ms cosine-squared ramps) at 70 dB SPL were recorded for tonotopic mapping. Tones were presented in a pseudorandom sequence at a rate of 1 Hz; each tone was repeated for 30 trials.

2.5. In vivo data analysis

The performance of μECoG arrays were tracked for over one year of implantation. We report standard measures of interfacial stability and expand on our previously published measures [74] to better capture spatially varying signals over time. Here, we provide improved metrics to describe long-term reliabilityof high-channel arrays, including conventional biotic and abiotic factors, with an extended consideration for spatial variation.

First, we employed mixed effects regression modeling to account for unintended sources of variation or irreproducible conditions. The consideration of random effects (RE) offers a lumped representation of any variations due to surgical implant, rat, or an individual device. In turn, we have a more conservative account of fixed effects (FE) variance. We reported the marginal significance of fixed factors using the likelihood ratio test (LRT) against models without fixed factors. Cross-validation was used to assess the predictive quality of our regression effects for novel recordings. Second, we conducted a more detailed analysis of the spatial field that revealed the magnitudes of spatially-varying field potential and noise from the same in vivo recording. From this analysis, we also extracted a length-scale parameter that describes the amplitude-invariant correlation structure of the spatial random field. This complete presentation allows for a more accurate measure of recording stability over time in chronic μECoG recordings.

2.5.1. Break-point analysis

A two-phase trend in time of electrode impedance was modeled with piecewise linear regression, including random slopes per electrode site, to mirror the initial recovery and the chronic stages of neural implant responses [71]. The transition point for the piecewise regression was determined from the maximum likelihood model from among all possible models of break-points. The break-point was used in subsequent regressions over electrode impedance to test possibly different relationships between impedance and signal metrics in the two implant phases. Mixed effects modeling was implemented with the lme4 package in R [78]. Throughout the report, the base-2 logarithm of in vivo impedance was used to provide better numerical conditioning and to interpret results in terms of doubling of impedance.

2.5.2. Spatial field analysis

We used spatial statistics to assess the stability of the spatially distributed μECoG signal over time. Based on previously published spatial correlograms analysis [74], the present analysis revealed distinct noise and field components of the total signal variance. The random field covariance was analyzed with the isotropic semivariance function, defined as $\gamma \left(\Vert s_i-s_j\Vert \right)=\frac{1}{2}var\left\{x_t\left(s_i\right)-x_t\left(s_j\right)\right\}$ for signal x and spatial index s. For stationary fields, semivariance is an “upside down” view of the covariance function C(h) with the relationship γ(h) = C(0) − C(h). However, the semivariance estimator relies on signal differences, making it more robust against inhomogeneous channel variance and the common reference signal. We formed the empirical semivariogram cloud with estimates of variance in pairwise differences between electrodes. Variance for each pair was calculated from the interstimulus baseline timeseries, using samples taken every 50 ms to reduce temporal auto-correlation.

Classical semivariogram analysis [79] isolated two distinct components of the total signal variance: a spatially uncorrelated signal component (i.e., electronic and electrode noise) and a stationary field covariance. In μECoG recordings, the spatial field covariance is generated by the neural field potential. Any difference between the total signal variance (measured by mean-square voltage levels) and the field and noise variance was attributed to a spatially homogeneous “common” component. The Matérn covariance function, which describes a stochastic injection-diffusion process of fractional order [80], [81], was chosen to model the field component of the semivariogram. The Matérn function is commonly used in spatial statistics as a moderation between the exponential and Gaussian functions, which are unrealistically course or smooth, respectively. The covariance model yielded a length-scale parameter θ (units of mm) describing the amplitude-invariant structure of the neural random field. We also derived estimates of field signal and noise amplitudes from the height and the floor of the semivariogram, respectively.

We used a hierarchical Bayesian model to estimate components of the field semivariance—maximum spatial variance (ζ, μV²), noise floor (σ_n, μV²), and length-scale (θ, mm) — as well as residual variance ε², taking advantage of sensible prior constraints (model details in Supplemental Materials). We then used Monte Carlo Markov Chain (MCMC) (implemented in PyMC3 [82]) to sample the joint posterior of {ζ,σ_n,θ} given the empirical semivariance. By taking square roots, the magnitude of signal variation between channels (RMS_s), and the magnitude of the noise (RMS_n) were directly compared to the conventional RMS_t voltage metric computed from temporal variation. A “Bayesian” goodness of fit coefficient (similar to [83]) was computed by comparing the median posterior value of the modeled residual variance ε² from the hierarchical model with the sample variance of the empirical semivariance. For semivariance observations γ_n computed from N electrode pairs,

$$r_B^2=1-\frac{N\text{med}\left\{{\epsilon }^2\right\}}{{\sum }_n{\left({\gamma }_n-\overline{\gamma }\right)}^2}$$

2.5.3. Evoked signal to noise ratio (ESNR)

For the following response-based metrics, we omitted channel-trial samples from a recording session using a two-stage outlier detection rule based on RMS voltage during a response or baseline window. Samples outside the 10–400 μV RMS range were rejected, and the interquartile range “box plot rule” was used to select outliers (greater than 4 IQR units) from the remaining samples.

The gain of tone-evoked response waveforms over baseline activity was computed following the Mahalanobis distance measure we previously reported [61]. Response magnitude was computed from the maximally-evoking tone, which was determined for each site. To compensate for the bias incurred by selecting the largest responses, the ESNR denominator was computed with the largest equivalent percentile of baseline-to-baseline Mahalanobis distances. Statistical significance of an ESNR value was determined with multiple comparison control by permutation testing at the level of individual recordings. The maximum ratio among sites (“max-SNR”) was recomputed 5000 times with shuffled response and baseline trials, and empirical p-values were referenced to the quantiles of these ratios.

2.5.4. Stimulus decoding

We employed the linear classifier described in [74], [84] to predict tones given array responses. Response covariates were concatenated from the field potential at each channel, bandpass filtered from 2–100 Hz, and windowed from 5–80 ms following each tone presentation. A channel was fully omitted from the classifier if more than 5% of its responses were outlying. For channels with a lower number of outlying responses, such samples were imputed from the surrounding array channels using image in-painting that iteratively filled masked pixels based on points bordering the missing regions. Tone decoding was summarized by accuracy (the proportion of successfully classified trials) and the average error of classification, measured in octave difference between the predicted and true tone.

2.6. Regression models of response metrics for impedance

We assessed the relationship between electrode impedance and responses metrics using (generalized) linear mixed-effects modeling ((G)LMM). Random effects regression terms were adopted to control for variations in post-implantation sampling and irreproducible conditions such as electrode/implant variation. We omitted per-session random effects to avoid confounding the potential correlation between electrode impedance and implant age. Logit-link logistic regression was used for the binary outcome of tone classification. A strong mean-variance association in classification error suggested log-link negative-binomial modeling. We assessed the ability of (G)LMMs to predict response values for hypothetical (novel) electrodes by excluding each electrode or implant group g in turn and calculating conditional expectations ${\widehat{y}}_i{}^{\backslash g}$ with random effects set to the mean value zero. The cross-validated coefficient of determination $r_{CV}^2$ was used to summarize predictive power in linear models:

$$r_{CV}^2=1-\frac{{\sum }_g{\sum }_{i=1}^{N_g}{\left(y_{g,i}-{\widehat{y}}_i^{\backslash g}\right)}^2}{{\sum }_k{\left(y_k-\overline{y}\right)}^2}.$$

MacFadden’s pseudo r², = 1 – log L_m/log L_null formula, comparing the log-likelihoods of a proposed model and its null hypothesis, was substituted for predictions with GLMMs. Note that negative values of $r_{CV}^2$ may occur when the hold-out prediction is more variable than the observation.

3. Results

3.1. Accelerated aging

We grouped electrodes into multiple batches due to the variable lead times across manufacturers. Different cleaning processes were required to achieve acceptable yields: All LCP Batches and PI Batch 1 simply required an isopropyl alcohol wash, while PI Batch 2 required removal from its adhesive backing under weak UV followed by a rather delicate technique to manually extract arrays from their panel. There was high variability in the batch fabrication of PI samples. All samples that underwent soaking had categorically similar initial impedances in the range of 16 to 138 kΩ at 1 kHz (table 1). Initial site yields for soak testing samples were in the range of 50%−90% (49.2 sites average, 28 sites minimum). We reserved arrays with greater than 90% yield for future implantation.

Table 1.

Characterization of μECoG arrays and projected lifetimes.

Batch	Sample ID	Mean Initial Impedance (kΩ) ± SD (initial sites)	Time Elapsed (Days at 60°C)	Equivalent Lifetime (Years at 37°C)
LCP (Batch 1)	A1	138±96 (38)	41	0.6
	B1	25 ± 4 (47)	41	0.6
	C	37 ± 21 (56)	368	5.0
LCP (Batch 2)	D	16 ± 2 (60)	140	1.9
	E	24 ± 11 (53)	248	3.4
	F	30±48 (51)	248	3.4
	G	121 ± 158 (54)	248	3.4
PI (Batch 1)	A	17 ± 9 (54)	8	0.1
	B	77 ± 58 (54)	487	6.7
	C	40 ± 17 (58)	314	4.3
PI (Batch 2)	D2	58 ± 22 (44)	0	0
	E	59 ± 61 (28)	83	1.1
	F	46 ± 11 (43)	132	1.8

¹Sample inadvertently removed from study though determined to be still functional.

²Sample yield fell below 50% by the second day.

Initial results from PI (Batch 1) showed notable promise with 2 of the 3 samples having a predicted lifetime of 4–7 years (table 1, supplemental figure 2). However, subsequent devices fabricated with the same manufacturing methods by the same vendor had much shorter lifetimes at 1.1–1.8 years (with one sample failing after the initial day, table 1). These devices failed by delamination (figures 5(a-b)). Sample C from LCP (Batch 1) had an equivalent lifetime at 37°C of 5 years (table 1). Samples A and B from the same batch were inadvertently removed from testing, although they remained functional with 92% and 100% yield, respectively (supplemental figure 2). The failure mode of Sample C from LCP (Batch 1) and Sample D from LCP (Batch 2) was the degradation of the reference wire, and saline uptake along the cabling and ZIF connector. The noble “gold” reference wire proved to only have a “gold coating” on a sterling silver core, and hence, continued exposed to an aqueous environment led to significant corrosion that changed the impedance values, and deposited silver on the μECoG contacts (figure 5(c)). Energy dispersive spectroscopy of Sample C from LCP (Batch 1) confirmed this hypothesis (supplemental figure 3). Efforts to revive the failed samples included extensive chemical washes and temporary pulsing protocols. However, further examination of the samples revealed corrosion on the ZIF connector due to saline uptake during the extended soaking period (figure 5(d)). We resumed testing of Samples E-G from LCP Batch 2 in a revised soaking chamber, but only logged an additional 2 samples over 17 days of soaking at 60° C before the new chambers leaked saline. Water ingress between LCP encapsulation layers was not observed with any soaked samples (figure 5(e)). We did not detect any failure of the LCP electrodes from the accelerated aging assay, but rather failures due to the test chamber itself.

Figure 5.

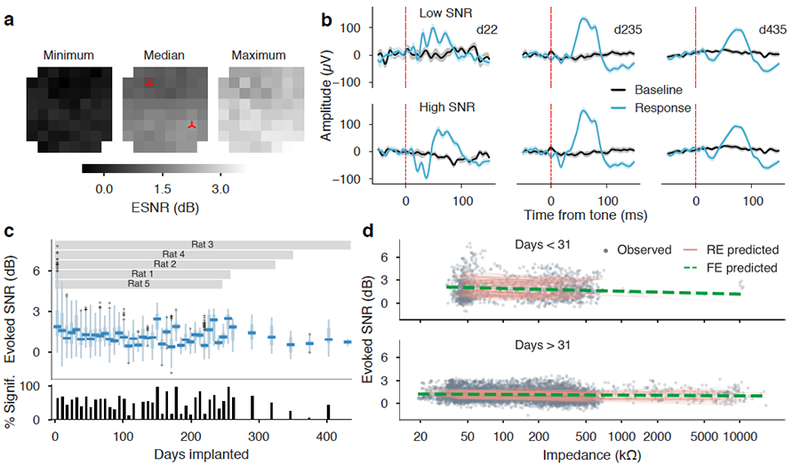
Evoked responses over the implant duration. (a) Longitudinal evoked-response metrics for one implanted rat. Array-oriented heatmaps show the minimum, median, and maximum values of electrode ESNR across 435 days of implantation. The spatial consistency in the array heat map illustrates consistent electrode performance from all sites on the array. (b) Response and baseline signals (trial average ± S.E.M.) for low- and high-SNR sites (marked on the heatmaps) reveal consistent features over one year of recording. (c) ESNR of electrodes from all implants were grouped in weekly bins and shown in box-plots, with the percentage of sites having significant ESNR (p<0.05) plotted below. The overall percentage of recordings with signal levels significantly above baseline was 52.8%. (d) A two-phase regression of electrode impedance from ESNR explained a small, but significantly greater amount of variance than an intercepts-only model (was not a significant factor in either the early or the late phase, and the model (${\chi }_2^2$ = 6.52 P < 0.05, LRT), However, impedance alone was a poor predictor of ESNR on novel data ($r_{CV}^2$ = 0.084).

3.2. Chronic electrophysiology

The LCP μECoG arrays demonstrated the longest predicted lifetimes following accelerated aging across multiple batch fabrication runs. These devices were subsequently implanted epidurally over core auditory cortices in five rats. A total of 136 recordings were collected at intervals of 1–2 weeks over the implantation period of 247–435 days (mean: 323 days). The endpoint of each implant was caused by sudden and irreparable loss of the headcap structure.

3.2.1. Baseline and response trends

3.2.1.1. Electrode impedance

We measured electrode impedance at 1 kHz at each recording session. The impedance followed a two-phase evolution, similar to results from intracortical studies [72], [85], [86]. For the purpose of linear modeling, the main trend was fit using impedance values below 1 MΩ. The maximum-likelihood model identified a break-point at 31 days (figure 4(a)). The first phase saw a doubling of impedance every 9 days–increasing by nearly a factor of 10–followed by a gradual halving of impedance over an estimated span of 119 days. In two implants, impedance levels returned to pre-implant levels by week 46. Figure 4 shows the predicted impedance trend over the entire sample of impedance measurements. High impedance measurements of 1 MΩ and greater were visibly separate from the main body of observations. However, only eight electrodes (3%) were measured with impedance greater than 1 MΩ for at least half of recordings. Six of these electrodes measured high impedance intraoperatively during implantation, while the remaining two electrodes measured high impedance in the second and 39th week respectively.

Figure 4.

Electrode impedance and baseline signal statistics. (a) Magnitude electrode impedance at 1 kHz showed two phases of evolution: an early, rapid rise followed by a more gradual decline. Break-point analysis estimated the transition to occur near the fourth week of implantation (31 days). (b) RMS electrode voltage in the 10–100 Hz bandpass, collected in weekly bins (RMS_t, box plots), follow a rise and decline roughly in phase with electrode impedance. Plotted on the same axes are the signal levels derived from spatial semivariance analysis. The estimated spatial variation (RMS_s, solid lines) and noise (RMS_n, dashed lines), depicted here in square-root μV units, also rose and declined in phase with impedance. The magnitude of spatial variation declined at a greater pace than the overall RMS voltage. (c) The semivariance model revealed a slowly changing length-scale of the background random field. Timeseries of posterior median estimates of length-scales, surrounded by 95% credible intervals, are plotted per implant. In contrast to the magnitude of spatial variation, the shape of the model covariance function remained relatively level with growth of 13.3 μm/wk. (d) Example semivariograms from an implanted rat effectively demonstrate changing amplitudes of neural field and the noise components, seen by the height of the curve and the y-intercept respectively. Median semivariance levels per inter-electrode spacing (black squares) were in good agreement with the semivariance model’s posterior distribution (spanned by the green margin).

3.2.1.2. Baseline signal levels

The RMS voltage measured at each electrode in the 10–100 Hz band (grouped into weekly bins, figure 4(b)) also followed rising and falling trends in approximately the same phase as impedance. Daily median values of impedance and RMS voltage were significantly correlated (Pearson r=0.54, p <10⁻⁸) Power spectral densities revealed that the rising and falling signal amplitude was consistent across frequency bands (supplemental figure 2).

The spatial semivariance measured in the same 10–100 Hz band summarized the magnitude of spatial variation in the array recordings and revealed the presence of an uncorrelated (noisy) process that was most likely not a component of the neural field potential. The magnitude of spatial power, depicted in square-root μV units in figure 4(b), peaked near 100 days before gradually declining. Noise levels followed a similar time course, with peak amplitudes of 10–15 μV. In one implant (Rat 2), the magnitude of spatial variation fell to within the average noise level by day 300, while other implants remained higher. During this phase of diminishing spatial variation, the temporal (or total) variation did not lessen. Both the noise and the signal power (after subtracting noise) were significantly correlated with median array impedance (Pearson’s r=0.71 and r=0.62, respectively P < 10⁻¹²).

Estimates of the Matérn covariance length parameter were fairly level, despite a shrinking amplitude of the spatial covariance. Median length-scale timeseries per implant (with 95% credible intervals) are plotted in figure 4(c). A weighted least squares regression for the length-scale trend (using means and variances of the posterior densities at each recording) showed a significant, gradual increase of 13.3 μm per week of implantation, or 1 mm per 75 weeks (F=17.2, p<0.001). Examples of spatial semivariograms observed at multiple points of one implant are shown in figure 4(d) to demonstrate notable changes in noise floor and spatial variance magnitudes. Despite the amplitude differences, the Matérn semivariance model fit the distribution of observed semivariance with an average $r_B^2$ of 0.414 ± 0.192 (mean ± std). Goodness of fit was furthermore not affected by the duration of the implant or the changing field amplitude (see supplemental materials for details). Additional semivariograms for select days across all implants are included in supplemental figure 5.

3.2.2. Tone-evoked responses

Tone-evoked responses remained detectable through the course of all implants. Figures 5(a-b) depict details of the longitudinal response measures for one implant. Heatmaps of the minimum, median, and maximum ESNR observed per site over 435 days show homogeneous performance within the observed range of response magnitudes (coefficients of variation were 1.8, 0.25, and 0.14 for each map, respectively) (figure 5(a)). Means and standard errors of evoked waveforms from early, middle, and late recordings were consistent throughout the implant for both low and high SNR channels (although there was significant variation across electrodes, supplemental figure 6). ESNR measures of each electrode were grouped into weekly bins along with a weekly series of the percentage of electrodes with ESNR significantly higher than baseline (p<0.05, max-SNR permutation test) (figure 5(c)). Median weekly ESNR remained above the 0 dB parity level for the duration of the study. We performed a logistic regression for the proportion of sites with significant ESNR using implant duration as the predictor and random effects per implant. There was no significant fixed-effects trend with time, suggesting that the variability of significant ESNR yield in time was small compared to variation across implants (LRT of the slope ${\chi }_1^2$ = 0.046, p = 0.831). The overall percentage of site recordings with significant ESNR across the study was 52.8% (3869/7332 observations).

As electrode impedance is implicated in both thermal noise and the tissue condition at the implant site, we evaluated whether electrode impedance was a reliable predictor of neural response metrics. We specified a LMM of ESNR versus impedance with nested random intercepts per channel and per implant (this being the most parsimonious combination of RE terms). The inclusion of a 31-day breakpoint was more efficient at reducing model deviance compared to a single-slope model of response SNR (${\chi }_{16}^2$ =1970.4, P < 10⁻¹⁵) additional degrees of freedom include random effects parameters 5(d)). The model including fixed effects for impedance was marginally more explanatory than a model using only intercepts (${\chi }_2^2$ 6.52 p <0.05 LRT) even through neither the early- nor the late-phase slope was a significant factor in isolation. Since a large amount of ESNR variance was explained by idiosyncratic responses by implant and by site, impedance was a fairly weak predictor of ESNR for hold-out observations on individual electrodes ($r_{CV}^2$ =0.084) We did observe that impedance was a strong predictor of the number of masked trials in the dataset. 66.6% of all trials that were masked due to high peak and/or RMS voltage levels (less than 1% of all trials) were recorded from electrodes in the highest decile of impedance (greater than 467 kΩ). In other words, trials were corrupted by artifact at a rate of 4.80% conditioned on an electrode having impedance in the highest decile, compared to a rate of 0.274% on average when the impedance was in the nine lower deciles.

3.2.3. Stimulus decoding

The frequencies of tones were predicted for a median of 754 trials (280 minimum, 1012 maximum) at each recording session using a linear classification scheme detailed in [74], [84]. Timeseries of tone decoding error are summarized in figure 6(a). Tone decoding accuracy is reported in supplemental figure 7. Both measures indicated an initial decline in the predictive content of μECoG recordings, followed by recovery and then stasis at levels exceeding uniform chance prediction.

Figure 6.

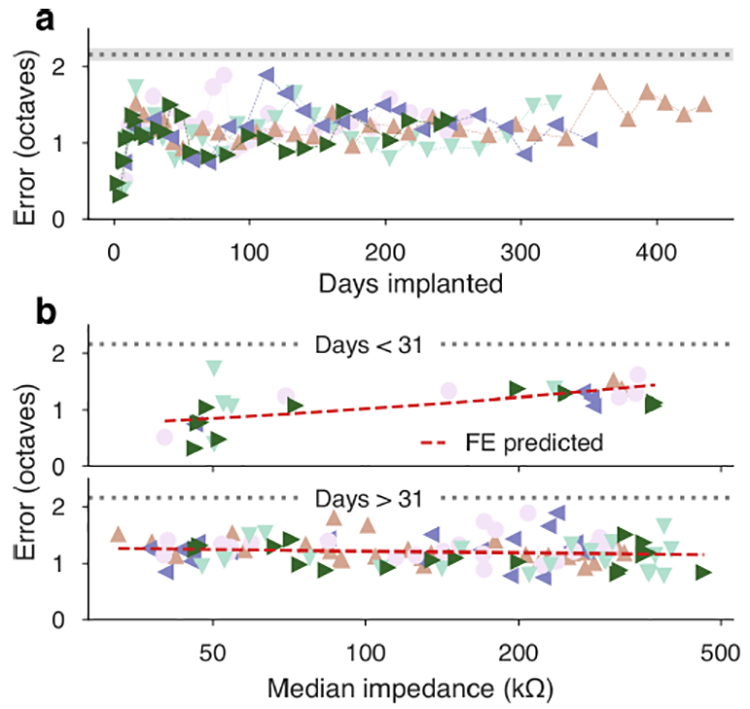
Tone decoding error by time and by electrode impedance. (a) Decoding error timeseries for each implant depicted an early degradation of tone specificity, followed by recovery between 50–100 days and a steady error level of 1.20 octaves. Uniform chance levels (estimated from simulated uniform classification) are drawn in gray margins. (b) Piecewise GLMMs (using the 31-day breakpoint of the impedance-by-day trend) linked array impedance to classifier outcome more efficiently than single-slope regressions. Early doubling impedance predicted a multiplier of 1.167 octaves of error, but there was not a significant late slope. Cross-validated R2 was less than zero for late-phase predictions. This indicates stable performance of the electrode interface out to one year and beyond.

We also inspected the putative effect of electrode impedance on decoding outcomes. To assess the correlation, we specified GLMMs (with random slopes per implant) linking accuracy and error to median array impedance. In both cases, a piecewise regression (with four additional fixed and random degrees of freedom) split at the impedance breakpoint of 31 days was significantly more effective at reducing the model deviance compared to single-slopes (LRT ${\chi }_4^2$=654.45 error,${\chi }_4^2$=919.2 accuracy p < 10⁻¹⁵) and had overall cross-validated R2 of $r_{CV}^2$=0.004 (error) and $r_{CV}^2$ =0.306 (accuracy). However, in both cases the explanatory and predictive powers of the impedance models were dominated by the early-phase association, which predicted a loss of −0.385 in log-odds of accuracy and gain in error of 19.9% per doubling of median array impedance. Compared with models using only early phase trends, the late phase impedance regression was not significant for error ${\chi }_1^2$ =1.287,P = 0.257) or accuracy (${\chi }_1^2$ = 2.9995, P =0.084). Both models provided predictions with $r_{CV}^2$ < 0 when considering late observations only. Figure 6(b) summarizes the error model and see supplemental figure 7 for the accuracy model.

4. Discussion

In this work, we further examine the interplay between biotic and abiotic mechanisms in the chronic reliability of high-density μECoG devices. We report stable μECoG performance for over one year of implantation based on standard measures of device characterization, in vivo responses, and a spatial semivariance analysis. Our conclusions also show that impedance predicts signal quality and information content in the first 31 days of recording, but not in the chronic stage (>31 days) because impedance decreased yet signal metrics remained constant. The 31 day breakpoint overlaps with the transition from acute to chronic tissue response in rat [68], and we posit that the slight decrease in impedance over time is likely due to changes in the tissue composition at the implant site, and not the result of a mechanical failure of the device, as our in vitro testing predicts stable impedances out to 3.4 years. Overall, these findings support the conclusion that μECoG arrays can reliably perform in chronic neural applications for over 1 year.

4.1. Low-cost manufacturing for rapid prototyping of μECoG arrays

The μECoG devices tested in the current study were manufactured using microfabrication methods based on flexible printed circuit board manufacturing. This approach has the advantage of providing high-density designs in large volumes at very low cost relative to standard photolithographic, wafer-based, thin-film manufacturing. It is also suitable for widespread dissemination across many neuroscience applications. When batch-processed, our flexible designs cost approximately $13 per device compared to commercially available neural arrays with comparable specifications at $500-$1000 per device [51]. Additionally, the materials under investigation in this study (e.g., gold, PI and LCP) are known biocompatible materials [54]–[58], and currently on the market in several clinical devices [52], [53]. To date, our LCP arrays have IRB approval for intra-operative investigations.

We also report several limitations in our manufacturing strategy for PI devices. The core challenge we found was inherent variability within the PI device manufacturing process, resulting in reduced overall device yield. We optimized the PI devices through iterative manufacturing runs, on-going soak testing, and extensive evaluation of post-process cleaning methods (e.g., chemical washes, sonication, transient biasing, and UV exposure). Ultimately, we chose not to perform in vivo testing on the PI devices based on inconsistent device performance during in vitro tests. However, the LCP stack-ups and geometries presented in the current long-term study demonstrated >95% initial yields and stable impedances for at least 3.4 years. Continued testing of several LCP samples is underway in a revised chamber to correct for short-comings observed in the current aging study.

4.2. Reliability metrics for high-density device characterization in vivo

Standard measures of electrode-tissue stability describe several biotic and abiotic factors. Previous reports track in vivo performance, such as decoding capability [2], [6], [8], [87] or behavioral thresholds [88]–[93], and measures of cellular health or injury [1], [66]–[68], [71], [94]–[98]. From an electronics’ perspective, abiotic metrics of recording electrode reliability often include impedances or measures of encapsulation stability [62], [66], [72], [99], [100]. However, the emerging interest in decoding integrated dynamics over broad cortical regions suggests that models of spatial variation would likely offer improved insights into signal stability and coupled biotic-abiotic interactions in chronic, reliable, high-density interfaces. Prior work has characterized signal variations and noise contributions at single recording sites from hardware, electrode-electrolyte interface, and biological sources in spike recordings with intracortical devices [101], [102] and depth local field potentials with micro-electrodes.

In the current study, our spatial semivariance analysis provided a simultaneous measure of the spatially varying signal power and noise from the same in vivo recording. This measure is sensitive to the loss of spatial specificity, as in the case of Rat 2 where the spatial power declines to the noise floor despite total signal variation remaining larger than noise. Unlike our previously reported spatial correlation analysis, our present model decoupled the length-scale and the amplitude of spatial variation. Identifying these aspects separately suggested a pattern of site-to-site covariance that did not abruptly change in spatial range but that amplified and then dampened over time. Interestingly, signal variance measured spatially (as differences between electrode sites) did not reach the same levels as the median variance measured temporally (figure 4(b)). The divergence was most striking during the rapid decline of spatial variability after approximately 2–3 months of implantation. The sustained level of total signal power indicates a variance component that is common to all channels and may be a signal attributable to the reference electrodes.

Statistics of the population dynamics are valuable features to consider in chronic recordings because of the inherently distributed information recorded by high density μECoG arrays [103–105]. Future work in tracking components of spatial variation over time would be well suited to a wide variety of implantable high-density interfaces with known interelectrode distances. This could include most planar arrays, such as spinal cord paddle leads and other ECoG devices, as well as multi-shank tissue penetrating structures. The applicability of spatial characterization to other multi-electrode interfaces may be expanded provided that additional methods (such as imaging) are employed to robustly determine interelectrode spacings across all implanted contacts.

4.3. The predictive relationship between chronic in vivo impedance and signal quality

The correlation between impedance and signal quality is potentially a critical relationship in neural prosthetic technology, as it may inform improved electrode designs and aid in adaptive site selection algorithms with chronically implanted high-density interfaces. It is generally concluded that electrode impedance produces negligible filtering distortion when coupled with modern high-impedance amplifiers [106]. However, a conclusive relationship between in vivo impedance and signal quality over time has yet to be achieved [98]. Several works report that impedance, tissue response, recording quality are correlated [72], [85], [103], [104], while others demonstrate no correlation between impedance and signal quality [5], [6], [105].

Our regression analysis showed some correlation between rising in vivo impedance and declining signal quality and information content in the first 31 days of recordings. In the chronic phase (>31 days), the impedance trend reversed slope and thereafter revealed no correlation with decoding output or evoked SNR. Impedance measurements of implantable electrodes capture the differential contributions of the electrode-electrolyte interface and the local biological activity. If the thermal noise of the electrode were the dominant noise source in vivo, we would expect signal quality trends to be correlated with impedance [86]. Instead, we found impedance correlated throughout the study with raw signal (and noise) amplitudes, but only correlated transiently with evoked response-based signal quality. The lack of any late-phase impact from decreasing impedance suggests that biological variations were the dominant factor that decreased the utility of the recording in the early phase of implantation. This hypothesis was further supported because site impedances remain categorically stable throughout the implant lifetime, and our accelerated aging results predicted device lifetimes exceeding 3.4 years in vivo. Biological sources of increased impedance in the first 31 days could be the result of increased resistivity of the surrounding encapsulation tissue, or a significantly higher impedance “interface layer” on the electrode surface resulting from biofouling [98], [106], [107]. Our identification of the 31-day breakpoint seems to align with the transition point between the short-term and long-term phases of tissue evolution at the electrode interface [69], [71], [108].

A final limitation to consider in evaluating the predictive nature of impedance and chronic signal quality is the spectral content of the recorded signal. The 1 kHz perturbation signal is the historic convention as it marks the strongest power of the spiking neural response. However, impedance relationships with μECoG arrays may be improved if a test signal with a lower frequency were employed. While multi-frequency trends have been reported to match 1 kHz changes in microwires [72], longitudinal ECoG studies have tracked impedances collected with a 20 Hz test signal [7]. It is possible that the subtle differences between frequency-dependent trends may improve the predictive relationship between impedance and signal quality for μECoG arrays.

5. Conclusion

In this work, we offer a baseline characterization of μECoG reliability and performance for over one year of implantation. A cross-validation of signal quality against impedance yielded insight into a predictive correlation only during the first 31 days of recording. Our main findings also offer a model of spatial variation as a measure of recording stability, which is otherwise concealed in standard RMS calculations with high-density μECoG arrays. The long-term reliability of the μECoG arrays shown in this study supports their potential for chronic clinical neural interfaces.

Figure 3.

LCP μECoG arrays showed no signs of degradation following accelerated soak testing after failures in the soak testing setup were corrected. a) PI (Batch 1), Sample C failed by delamination after 9 days of accelerated soaking; b) PI (Batch 2) Sample D failed by delamination after 191 days of accelerated aging; c) LCP (Batch 2), Sample D showed crystal growths due to the dissolution of its reference wire in solution; d) LCP (Batch 2), Sample D had a corroded ZIF connector due to saline leaking from the soak testing chamber; and e.) LCP (Batch 2) Sample G after 231 days of accelerated soaking appears indistinguishable from images taken prior to soaking began. Soaking is ongoing after the soak testing procedure was corrected.