Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2019 Jan 24.
Published in final edited form as: Eur Biophys J. 2014 Sep 12;43(10-11):555–564. doi: 10.1007/s00249-014-0985-6

Modeling of RNA nanotubes using molecular dynamics simulation

S R Badu 1, R Melnik 2, M Paliy 3, S Prabhakar 4, A Sebetci 5, B A Shapiro 6
PMCID: PMC6345520  NIHMSID: NIHMS1003702  PMID: 25208764

Abstract

In this study, we construct novel RNA nanoclusters, RNA nanotubes made of several nanorings up to the size of 20 nm, utilizing the molecular dynamics simulation, and study their structural properties [i.e., the root mean square deviation, the radius of gyration and the radial distribution function (RDF)] in physiological solutions that can be used for drug delivery into the human body. The patterns of energy and temperature variations of the systems are also discussed. Furthermore, we study the concentration of ions around the tube as a function of time at a particular temperature. We have found that when the temperature increases, the number of ions increases within a certain distance of the tube. We report that the number of ions within this distance around the tubes decreases in quenched runs. This indicates that some ions evaporate with decrease in temperature, as has been observed in the case of the nanoring. RDF plots also demonstrate a similar trend with temperature, as was found in the case of RNA nanorings.

Keywords: RNA nanocluster, Nanotube, Drug delivery, Cancer therapy, Bionanotechnology

Introduction

Ribonucleic acid (RNA) is a strand composed of the nucleobases Cytosine, Guanine, Adenine and Uracil. These nucleobases are connected to the sugar ring and then to the phosphate backbone to construct a complete strand. There are several structural derivatives of RNA modeled in literature in the nanoscale range (Holbrook 2005; Ishikawa et al. 2013; Jaeger et al. 2001). One of the most significant developments of RNA nanostructures is in the design of RNA nanorings, nanotubes (Grabow et al. 2011; Afonin et al. 2012; Badu et al. 2014), and other nanostructures of different geometrical structures. In the field of nanotechnology, RNA has several potential applications due to its relatively high thermal stability, flexible structure and variety of functions. For instance, RNA can produce a number of structural motifs via intermolecular interactions (Leontis et al. 2006), useful for applications in nanoparticles and nanodesign.

A computational study has been done (Yingling and Shapiro 2007) to develop the structural design of RNA nanorings and nanotubes using molecular dynamics (MD), where a RNA nanoring is formed by assembling a linear chain of RNA through a non-covalent loop–loop interaction. The combination of nanorings in a pile forms the RNA nanotube. During MD simulations, the base pairing between the two loops has been maintained and the angular variation between the loops is traced (the angle between loops varies around 120°). RNAI and RNAII are two kinds of double-stranded fragments of RNA that can be combined in different ways. After some modifications in the combinations, the nanoring building block is formed. Furthermore, the building blocks of nanorings are engineered in such a way that the RNAI and RNAII ends are complementary to each other. The complexation of these two RNA fragments via sticky ends is an important feature for construction of nanoclusters like RNA nanorings and nanotubes. In short, by using six helical building blocks of either one or two types (RNAI/RNAII), the nanoring is formed by their self-assembly via base-pairing hydrogen bonds. The stability of the nanoring depends on RNAI/RNAII interactions. The design of the sticky ends helps to assemble the nanorings to build the nanotubes. The starting structures of the RNAIi/RNAIIi (double-strand RNAs) complex are taken from the protein data bank with the pdb code (2bj2.pdb) (Lee and Crothers 1998). RNAI and RNAII are small strands of RNA known as sense and antisense plasmids. These RNAs are used to control the replication of the ColE1 plasmid of Escherichia coli. During the process of coli replication, the double helix of RNAI/RNAII is formed by the pairing of seven nucleotide loops from each of the RNAs. Such loops that pair to each other to form a double helix are known as kissing loops. The details of the formation of these loops are described in Tomizawa (1984, 1986). Recently, RNA has been self-assembled to build nanoscale scaffolds (Afonin et al. 2010) using computational techniques and experiments. It is reported in the literature that several forms of RNA motifs can be constructed to provide a proper multifunctional RNA nanocluster; however, a very few of them are found to be useful for drug delivery. Assembly should be used to build the RNA nanocluster from RNA building blocks (Shu et al. 2011). The RNA nanoclusters have various applications in nanobiomedicine. In particular, the RNA nanoring and the nanotube can be used for the delivery of small interfering RNA (siRNA) to the human body. Because of the shape and size of the RNA nanoring and the nanotube, multiple siRNA nanorings can be packaged to deliver them to the proper position of the cancerous cell. If the nanotube is used for drug delivery, a larger amount of the drug could be packaged in the RNA nanotube in comparison to that of the RNA nanoring. Furthermore, there are two possible ways to deliver therapeutic drugs into the human body. Firstly, it can be done by directly including a drug into the RNA building blocks. Secondly, it can be done by attaching the drug at particular ends of the RNA nanotube. The RNA nanotube can be useful for many applications; in particular, for the delivery of drug into the human body due to its stable condition at all temperatures (Shu et al. 2011). The target delivery vehicle, i.e, the RNA nanoclusters built for drug delivery, should be stable, so the modeling of such structures is critical.

Furthermore, the hairpin-like structure of the nanocluster has been modeled (Lee et al. 2012) from RNA interference polymers. The discovery of ansiRNA (Kanasty et al. 2013) is one of the most important research achievements in this field. The siRNA is basically a synthetic, double-stranded RNA with 21 base pairs. The function of siRNA is to suppress the problematic genes by RNA interference. The delivery of oligonucleotides has also been studied to understand the effectiveness of models in the cancer therapy in humans (Yano et al. 2004).

Previously, our group [see Ref. Paliy et al. (2009)] studied the mechanical and thermodynamic properties of an earlier modeled nanoring (Yingling and Shapiro 2007) using the molecular dynamics method (Binder et al. 2004; Hansson et al. 2002), but such studies on RNA nanotubes have not been done. The results obtained for the nanoring were later supported by experimental results using biochemical and biophysical techniques (Grabow et al. 2011). Specifically, the issues addressed in this previous paper were the stability of the nanoring vs. temperature, the effect of the environment (i.e., solvent and counteractions) on its stability, and the conformations and dynamics under external force. Some anomalous behavior has been observed with variation of the temperature of the simulation box containing the nanoring. In a recent study, the properties of human immunodeficiency virus (HIV) on hairpin-like subtype-A and subtype-B at different salt concentrations and magnesium bindings were explored using molecular dynamics techniques (Kim and Shapiro 2013). Also, an experimental study of the concentration dependence of NaCl and KCl on free energy of RNA hairpin folding has been done (Vieregg et al. 2007). Such studies provide additional motivations to conduct MD simulations of RNA nanoclusters.

Furthermore, the first coarse-grained model for RNA nanoring has been developed (Paliy et al. 2010) by utilizing the molecular dynamics simulations method. The authors reported simulation times ranging from several nanoseconds up to a microsecond with increasing cluster size. The basic idea in their work was to approximate a part of the nucleotide as one-bead or three-bead structures, where the phosphate group is taken as the first bead, the sugar ring is taken as the second bead, and the nucleobase is taken as the third bead. Here, two types of beads are similar in the sense of location, but the third type of bead is placed at the 1N or 9N position, depending if it is pyrimidine (UC) or purine (AG). In practice, the molecular dynamics simulations should be long enough to achieve a suitable conclusion from the results.

The root mean square deviation (RMSD) is a vital parameter to characterize the equilibration of a molecular dynamics simulation. Mathematically, the RMSD in the MD simulation can be expressed as

RMSD(t1,t2)=[1N∑i=1N‖xi(t2)−xi(t1)‖2]1/2, (1)

where xi(t) is the position of the ith atom at time t, and N is the number of atoms in the molecule. In traditional calculations, the position at t1 is taken as a reference point and then the RMSD(t1, t2) is calculated for t2 > t1.

The radius of gyration of a system describes the structure change during the molecular dynamics simulation. It can be defined as the weighted scalar distance of each atom from the center-of-mass. It is given by the following formula:.

Rg=∑r2mi∑mi, (2)

where mi is the mass of the ith atom in the molecule.

The radial distribution function of a system of particles describes the variation of density as a function of the distance from a reference particle. Mathematically, the radial distribution function can be expressed as

g(r)=4πr2ρdr, (3)

where ρ=NV is the number density of particles, where V is volume of the system.

In this paper, our aim is to connect several hexagon-shaped RNA nanorings to form the RNA nanotube and to study properties of the resulting structure. We submerse RNA nanotubes in physiological solutions to create an environment similar to human body fluid and then perform all-atom MD simulations. From the obtained trajectories, we study the structural properties, including radial distribution function, RMSD, radius of gyration and the ionic distributions around the tube. We then use these all-atom MD trajectories to develop a coarse-grain model for longer time range simulations, to make our results compatible with the time range of biological processes, which are more suitable for bionanotechnology.

The rest of this paper is organized as follows. In Sect. 2, we describe the computational methodologies used for calculations. The results are presented and discussed in Sect. 3. Concluding remarks and an outlook are then stated in Sect. 4.

Computational details

Here we have performed all-atom molecular dynamics simulations of RNA nanotubes by using the CHARMM27 force field (Phillips et al. 2005) implemented in the NAMD package (MacKerell et al. 1998), as has been done for the nanoring (Paliy et al. 2009). The modeling of the nanotube, visualization and the analysis of the simulation outputs were performed using the software VMD (Humphrey et al. 1996). The RNA-nanotube was solvated in a water box. The size of the box is taken in such a way that the distance from the surface of nanocluster to the wall is slightly larger than the cutoff radius used in the MD simulation. In order to make the system neutral, we added 594, 924, 1,254 and 1,584 23Na+ for two-ring, three-ring, four-ring and five-ring nanotubes, respectively. Furthermore, to make the solution equivalent to the physiological solution, we added extra 594, 924, 1,254 and 1,584 23Na+ and 35Cl− ions to the two-ring, three-ring, four-ring, and five-ring RNA nanotubes, respectively. This system was simulated at constant temperature and pressure using the NAMD software. The temperature in the system was controlled by using the Lan-gavin method with damping η = 5ps−1 and the pressure was controlled by the Nose–Hoover piston method (Feller et al. 1995; Martyna et al. 1994). The periodic boundary conditions were applied during the simulation in all three dimensions. For adding chemical bonds between the segments in the nanoclusters, we used the topotools available in the VMD.

Results and discussion

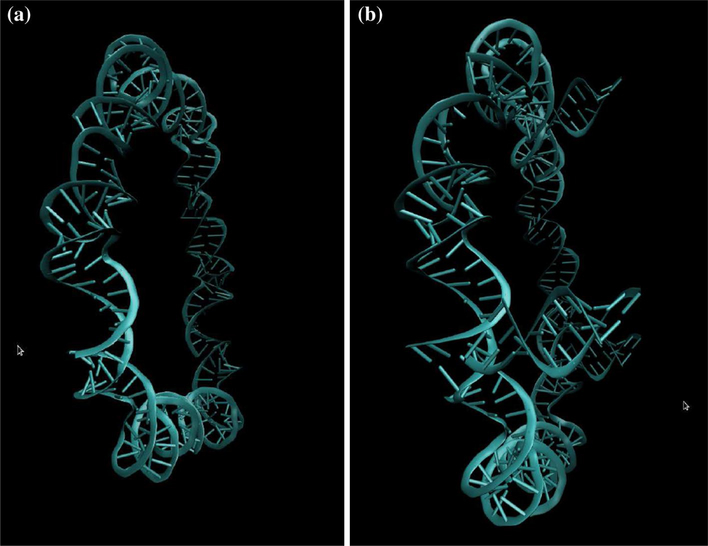
Starting from previously modeled nanoring structures, we modeled the RNA nanotubes with two, three, four and five nanorings. In order to demonstrate the construction of the nanotube, we have presented both the nanoring itself and the ring including tails used to link the two nanorings, in Fig. 1a and b, respectively. Also, a sample structure of the five-ring nanotube with its front and side view is presented in Fig. 2. The nanoring presented in Fig. 1a is constructed from the six helical segments of the RNA double strand described in more detail in Paliy et al. (2009) and Paliy et al. (2010). Each segment is built from the kissing loops of the RNAIi/RNAIIi complexes.

Fig. 1.

Fig. 1

Open in a new tab

a RNA nanoring and b RNA nanoring, including the tail to connect to the second ring to model the RNA nanotube

Fig. 2.

Fig. 2

Open in a new tab

RNA nanotube assembled from five nanorings. a Front view, b side view

As we mentioned earlier, the RNAIi and RNAIIi are double-strand RNAs. By using the VMD tools, we were able to connect multiple rings via three links at junctions presented in Fig. 1b. The links used in connecting the multiple numbers of nanorings (to build the RNA nanotube) are composed of helical double-stranded RNAs with 22 nucleobases. Three links are used in between two consecutive rings to connect them to form nanotubes, as shown in Fig. 1b. In an earlier experimental study, the hexagonal structure of the pRNA was modeled in order to package the viral DNA into the cell (Guo et al. 1998). In this previous work, the building blocks for the hexamers were taken from the work of Bailey et al. (1990). The base pairing between the lower and upper ends is responsible for self assembly of the building blocks. The hexamer structures developed in our investigation are similar to this previous work. The difference is that the building blocks in our work have been constructed from the RNAI/RNAII complex as discussed in Sect. 1, whereas those for the earlier work (Guo et al. 1998) have been constructed from pRNA. The chemical bonds between the ring and the links are mediated through the phosphorous of the phosphate group in the ring and the oxygen in the sugar ring of the corresponding link or vice versa. The chemical bonds added between different segments are optimized using NAMD.

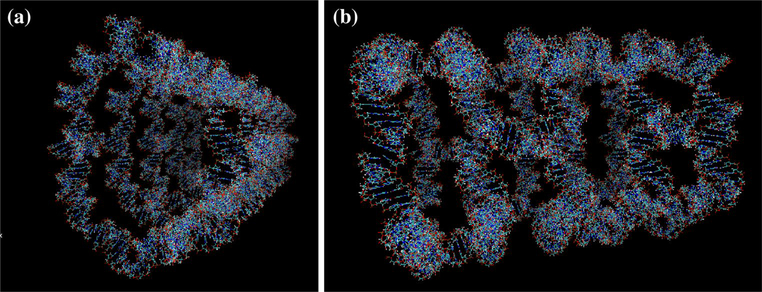
The nanotubes solvated in the salt solution including 23Na+ and 35Cl− ions are presented in Fig. 3. Similar model solutions were prepared for all other nanotubes and implemented by the MD simulation at NVT for the time period of 1 ns.

Fig. 3.

Fig. 3

Open in a new tab

VMD-generated RNA nanotube in water and salt to match physiological solutions. a Tube with four rings, b tube with five nanorings

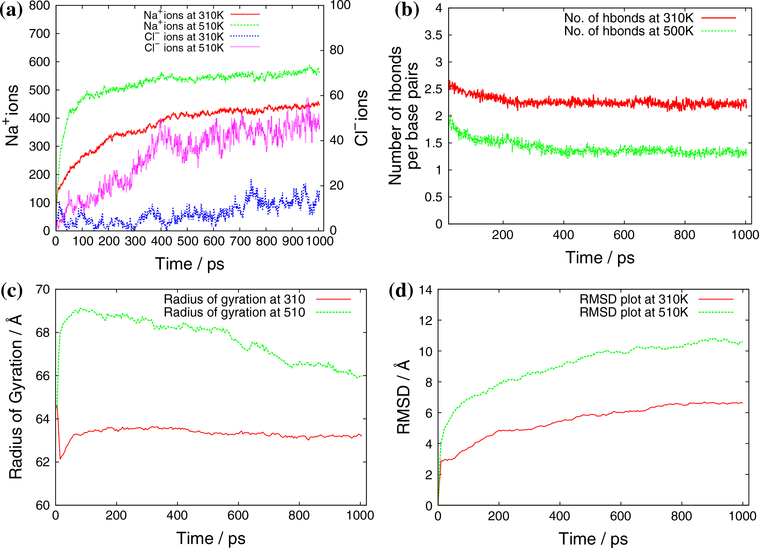
Now we discuss the results obtained from the MD simulation for different sizes of nanotubes. The results for the simulation of two-ring nanotubes are summarized in Figs. 4 and 5. Figure 4 shows the variation of energy and temperature with simulation time. At the beginning of the simulation, the energy of the system varies and then becomes stable once the system becomes stabilized. Here in our results, we have presented only the later part of the simulation, which is also known as the production region of simulation. This is the region in which we will do all our analysis. The temperature of the system remains almost stable, with some fluctuations. In Fig. 5, we present the calculated properties, such as the number of ions around the RNA nanotube within a distance of 5 Å at different temperatures, the number of bonds per base pair, the radius of gyration, and the RMSD at two temperatures, 310 and 510 K.

Fig. 4.

Fig. 4

Open in a new tab

a Energy and b temperature vs. simulation time for the all-atom MD simulation of two-ring RNA nanotubes in water and salt

Fig. 5.

Fig. 5

Open in a new tab

a Number of ions with the range of 5 Å, b number of bonds per base pairs, c radius of gyration and d RMSD of two-ring RNA nanotubes obtained from an all-atom MD simulation

From Fig. 5a, it is clear that at a particular temperature, the number of 23Na+ ions continues to increase before stabilizing in the production region of the MD simulation. In the production region, it seems that most of the 23Na+ ions are localized around the surface of the RNA nanotube. This is because of the existing negative polarity of the phosphate group. On the other hand, the number of the 35Cl− ions remains very low around the radius of 5 Å from the ring of the nanotube, as expected. These results are reminiscent of the earlier calculations done for the RNA nanoring using all-atom MD simulation (Paliy et al. 2009). If we change the temperature from 310 to 510 K, the number of 23Na+ ions increases with temperature similar to the characteristics found in the earlier studies. The characteristics observed in our study show the validity of nanoclusters modeled from RNA building blocks by using an all-atom molecular dynamics simulation. This also indicates that the characteristics obtained for the smaller nanoclusters can predict similar characteristics for larger clusters. Furthermore, in Fig. 5b, we have described the number of bonds between the base pairs inside the tube at two temperatures, 310 and 510 K. From the plot, it is clear that the number of bonds per base pair remains constant throughout the simulation for a particular temperature; however, the number of bonds per base pair decreases going from 310 to 510 K. This is due to thermal effects in the system. These studies describe the stability of the structure during the simulation at a particular temperature.

In Fig. 5c, we have presented the radius of gyration for the two-ring nanotube at two different temperatures. At 310 K, the radius of gyration goes on increasing at the beginning of the simulation, but later on it decreases and becomes stable at the end of the simulation, indicating the simulation has become saturated. At a temperature of 510 K, the radius of gyration shows some drastic variations at the beginning as in the case of 310 K, but instead of being constant at the end, it keeps on decreasing very slowly until the end of the simulation, contrary to that at 310 K. As we described in Sect. 1, the radius of gyration is a rough measurement of compactness. This indicates that the compactness of the system is decreasing slowly with time at 510 K. This phenomenon, observed during our simulation, indicates that the compactness of our system is decreasing, and hence the system will become collapsed if the simulation is performed for a significant period of time. A similar trend has also been observed for the RNA nanoring in our earlier study. Furthermore, Fig. 5d shows that the root mean square deviation increases at the beginning of the simulation and then becomes stable at the end of simulation. The root mean square deviation at the end of the simulation is around 6 Å at 310 K and it is around 10 Å at a temperature of 510 K.

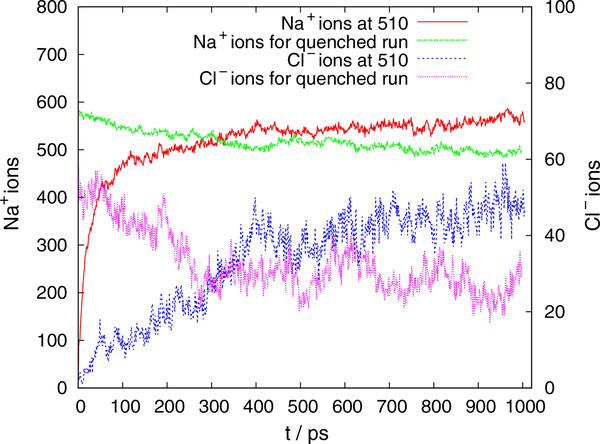
We have also performed the simulation for the quenched system, where the system simulated at 510 K was again supplied for the MD simulation at 310 K. The ionic distribution with time for the quenched run is shown in Fig. 6. From the plot, it is clear that the number of ions drops down as the temperature is decreased. This indicates that there is evaporation of the ions with decreasing temperature. Similar trends have been observed for the other RNA nanostructures.

Fig. 6.

Fig. 6

Open in a new tab

Number of 23Na+ and 35Cl− ions with the range of 5 Å at 510 K and the quenched run at 310 K, to see the evaporation of ions as temperature decreases

We have also performed the calculations for the RNA nanotubes with three rings, four rings and five rings, and found that the results are similar to those of the two-ring RNA nanotube. To show this, we have also presented the results for the five-ring nanotube in Fig. 7. Most of the properties we have studied are similar for nanotubes consisting of two, three, four and five rings, indicating that the characteristics of the nanotube are similar to those of the ring. One can predict the ionic distributions around the tube very easily for the larger nanotube sizes if all-atom MD simulations are feasible.

Fig. 7.

Fig. 7

Open in a new tab

a Number of ions with the range of 5 Å, b number of bonds per base pairs, c radius of gyration and d RMSD of five-ring RNA nanotubes obtained from an all-atom MD simulation

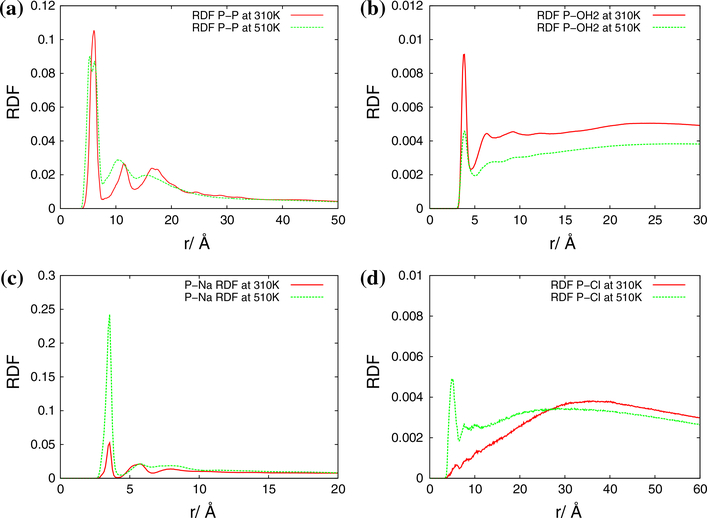
Next we describe the nature of radial distribution function (RDF) plots calculated for the RNA nanoclusters under study. The results for the RDF plots for the two-ring RNA nanotube are presented in Fig. 8. In particular, four subplots in this figure present the RDF plots for phosphorous–phosphorous, phosphorous–water, phosphorous–sodium and phosphorous–chlorine, respectively. From the P–P RDF plots, we see that there are peaks around 7, 11 and 18 Å. These peaks actually show the first, second and third nearest neighbors of the phosphorous atom, respectively. The intensity of the peaks is increased on going from 310 to 510 K. The position of the first peak is at the same position, whereas the second and third peaks are shifted slightly to lower distances in comparison to their positions at 310 K.

Fig. 8.

Fig. 8

Open in a new tab

Radial distribution function for the two-ring RNA nanotube. a P–P, b P–OH2, c P–Na, d P–Cl

Furthermore, from the P–OH2 RDF plots at temperatures of 310 and 510 K, presented in Fig. 8b, it is clear that for each RDF there is a peak around the distance of 4 Å, which indicates the first solvation shell around the phosphorous atom taken for the RDF plots. In the same way, the second small peak indicates the second solvation peak for the phosphorous atom in the phosphate backbone of RNA strands building the RNA nanotubes. In the rest of the range, the characteristics of the RDF plots remained more or less stable, indicating that the water molecules are distributed uniformly after a certain distance. In spite of showing a similar trend, the height of the first peak is significantly dropped on going from 310 to 510 K. This indicates that a significant amount of water molecules is expelled out from the surface of the RNA nanocluster at higher temperatures.

Again, the RDF plot for P–Na shows the first peak around 3.5 Å at both temperatures, 310 and 510 K, indicating that most of the sodium ions are around this distance at the end of the all-atom MD simulation. The only difference between the RDF plots at 310 and 510 K is that the first peak of the distribution function is significantly increased, which supports our conclusion from the ionic distribution plots in Fig. 5a. Furthermore, from the RDF plot for P–Cl, it is clear that the chlorine ions are far away from the surface of the RNA nanocluster at 310 K. When the temperature of the system is increased to 510 K, the 35Cl− ions are also aggregated significantly closer to the tube, as indicated by the first peak of the RDF plot at 510 K. The height of the peak at a distance in the RDF plot is proportional to the number of 35Cl− ions around that distance. This means the number of 35Cl− ions around the first peak at 510 K is larger compared to the number of such ions at 310 K, as observed from the plot for the number of 35Cl− ions at these two temperatures in Fig. 4a.

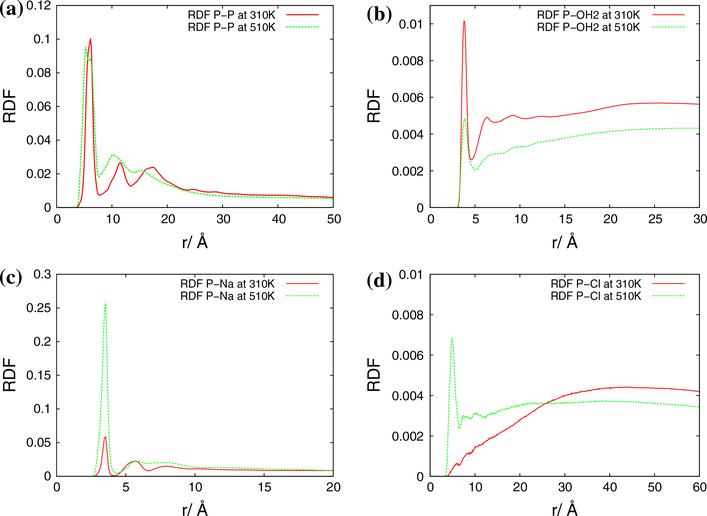
We have also calculated the RDF plots for three-ring, four-ring and five-ring RNA nanotubes. The solvation nature and ionic distribution during the MD simulation have been found to be similar to those found in the case of the two-ring nanotube. To show the similarity, we have presented RDF plots for the five-ring RNA nanotube in Fig. 9. For all of these systems, we see that the peaks for the P–P RDF remain almost same, for P–OH2, the intensity at the peak is decreased on increasing the temperature, but in the P–Na and P–Cl RDF plots, the intensity of the first peaks is significantly increased on increasing the temperature. From these observations, we can say that the number of 23Na+and 35Cl− ions are attracted toward the surface of the nanocluster and the water molecules are pushed away from the surface as the temperature is increased. In short, we observe that the ions are being precipitated around the surface of the RNA nanocluster as the temperature of the system is increased. Computationally, the nanoring structures are modeled by using the MD simulations in earlier studies (Paliy et al. 2009; Yingling and Shapiro 2007). For the nanoring self assemblies of the RNAI/II kissing loop complex, experimental studies have been reported in Grabow et al. (2011). During the experiments, the kissing loop complex was put in a pot and heated for 2 min up to 95 °C, and then later cooled down to 4 °C. At the end of the experiment, various kinds of self assemblies of the kissing loop complex formed. The self assembled species of the kissing loop complex were dried and supplied for further analysis. In particular, the side length and the diameter of the self-assembled nanoclusters have been measured. From the analysis, it has been found that there are three types of self assemblies for the RNAI/II complex: square, hexagon and octagon, with the diameters 10.6, 15.0 and 18.9 nm, respectively. Out of them, the hexagonal rings are found to be 80 %, which tells that the nanocluster is more stable in the form of a hexagonal ring. However, the atomic force microscopy (AFM) images of these systems are shown in Fig. 2e of Grabow et al. (2011). Unfortunately, the experimental results for the AFM or cryoEM of the nanotube system are not available.

Fig. 9.

Fig. 9

Open in a new tab

Radial distribution function for the five-ring RNA nanotube. a P–P, b P–OH2, c P–Na, d P–Cl

Conclusions and outlook

In our earlier paper (Paliy et al. 2009), we analyzed physical properties of the nanoring. The RNA nanoring is a small system in comparison to the nanotube and has limited practical applications in bionanotechnology. However, it provides an excellent testing ground for further studies. In our current study, for the first time, we have analyzed the optimized structures of nanotubes up to the size of 20 nm, including all the chemical bonds between different segments. The individual RNA nanorings were connected via double-helical rings mediated by the bonds between the phosphate group and sugar ring. The newly added bond lengths have been optimized by using algorithms available in NAMD. Then, starting from nanorings, the results for the RNA nanotubes of different sizes have been discussed in detail. Analysis of the results for stability of modeled tubes have been performed via study of the root mean square deviation, radius of gyration, number of hydrogen bonds per base pair, ion accumulation around the tube, and the radial distribution functions. Ion evaporation upon quenched runs has been observed in the case of all the nanoclusters studied. From our analysis results, it is clear that the quality of the results are likely to be further improved by doing the MD simulation for a longer time range. Studies of properties using a coarse-grained model that allows us to perform MD simulations for longer ranges of time are currently in progress. These longer time-range simulations would better reflect the time range of biological processes, typical for many applications in bionanotechnology. In its turn, these new results could complement our present findings and provide further guidance to experimentalists working in this field.

Acknowledgments

Authors are grateful to the NSERC and CRC Program for their support and Shared Hierarchical Academic Research Computing Network (SHARCNET: www.sharcnet.ca) for providing the computational facilities. RM and AS acknowledge TUBITAK support. Finally, we would like to thank Dr. P. J. Douglas Roberts for helping with technical SHARCNET computational aspects.

Contributor Information

S. R. Badu, MS2Discovery Interdisciplinary Research Institute, M2Net Lab, Wilfrid Laurier University, 75 University Avenue, Waterloo, ON N3L 3V6, Canada

R. Melnik, MS2Discovery Interdisciplinary Research Institute, M2Net Lab, Wilfrid Laurier University, 75 University Avenue, Waterloo, ON N3L 3V6, Canada

M. Paliy, Department of Mechanical and Materials Engineering, Department of Chemistry, Surface Science Western, University of Western Ontario, London, Otario N6A 5B9, Canada

S. Prabhakar, MS2Discovery Interdisciplinary Research Institute, M2Net Lab, Wilfrid Laurier University, 75 University Avenue, Waterloo, ON N3L 3V6, Canada

A. Sebetci, Department of Mechanical Engineering, Mevlana University, 42003 Konya, Turkey

B. A. Shapiro, Center for Cancer Research Nanobiology Program, National, Cancer Institute, Frederick, MD 20892, USA

References

  1. Afonin KA, Bindewald E, Yaghoubian AJ, Voss N, Jacovetty E, Shapiro BA, Jaeger L (2010) In vitro assembly of cubic RNA-based scaffolds designed in silico. Nat Nano 5(9):676–682. doi: 10.1038/nnano.2010.160 [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Afonin KA, Kireeva M, Grabow WW, Kashlev M, Jaeger L, Shapiro BA (2012) Co-transcriptional assembly of chemically modified RNA nanoparticles functionalized with siRNAs. Nano Lett 12(10):5192–5195 [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Badu SR, Melnik R, Paliy M, Prabhakar S, Sebetci A, Shapiro BA (2014) High performance computing studies of RNA nanotubes. In: Proceedings of IWBBIO-2014 [Google Scholar]
  4. Bailey S, Wichitwechkarn J, Johnson D, Reilly BE, Anderson DL, Bodley JW (1990) Phylogenetic analysis and secondary structure of the bacillus subtilis bacteriophage RNA required for DNA packaging. J Biol Chem 265(36):22365–22370 [PubMed] [Google Scholar]
  5. Binder K, Horbach J, Kob W, Paul W, Varnik F (2004) Molecular dynamics simulations. J Phys Condens Matter 16(5):S429 [Google Scholar]
  6. Feller SE, Zhang Y, Pastor RW, Brooks BR (1995) Constant pressure molecular dynamics simulation: the langevin piston method. J Chem Phys 103(11):4613–4621 [Google Scholar]
  7. Grabow WW, Zakrevsky P, Afonin KA, Chworos A, Shapiro BA, Jaeger L (2011) Self-assembling RNA nanorings based on RNAI/II inverse kissing complexes. Nano Lett 11(2):878–887 [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Guo P, Zhang C, Chen C, Garver K, Trottier M (1998) Inter-RNA interaction of phage 29 pRNA to form a hexameric complex for viral DNA transportation. Mol Cell 2(1):149–155 [DOI] [PubMed] [Google Scholar]
  9. Hansson T, Oostenbrink C, van Gunsteren W (2002) Molecular dynamics simulations. Curr Opin Struct Biol 12(2):190–196 [DOI] [PubMed] [Google Scholar]
  10. Holbrook SR (2005) RNA structure: the long and the short of it. Curr Opin Struct Biol 15(3):302–308 [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Humphrey W, Dalke A, Schulten K (1996) VMD: visual molecular dynamics. J Mol Graph 14(1):33–38 [DOI] [PubMed] [Google Scholar]
  12. Ishikawa J, Furuta H, Ikawa Y (2013) RNA tectonics (tectoRNA) for RNA nanostructure design and its application in synthetic biology. Wiley Interdisciplinary Reviews: RNA 4(6):651664. [DOI] [PubMed] [Google Scholar]
  13. Jaeger L, Westhof E, Leontis NB (2001) TectoRNA: modular assembly units for the construction of RNA nano-objects. Nucl Acids Res 29(2):455–463 [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Kanasty R, Dorkin JR, Vegas A, Anderson D (2013) Delivery materials for siRNA therapeutics. Nat Mater 12(11):967–977 [DOI] [PubMed] [Google Scholar]
  15. Kim T, Shapiro BA (2013) The role of salt concentration and magnesium binding in HIV-1 subtype-a and subtype-b kissing loop monomer structures 31(5):495–510 [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Lee AJ, Crothers DM (1998) The solution structure of an RNA looploop complex: the ColE1 inverted loop sequence. Structure 6(8):993–1007. doi: 10.1016/S0969-2126(98)00101-4 [DOI] [PubMed] [Google Scholar]
  17. Lee JB, Hong J, Bonner DK, Poon Z, Hammond PT (2012) Self-assembled RNA interference microsponges for efficient siRNA delivery N Mater 11(4):316–322 [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Leontis NB, Lescoute A, Westhof E (2006) The building blocks and motifs of RNA architecture. Curr Opin Struct Biol 16(3): 279–287 [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. MacKerell BD, Bellott D, Evanseck JD, Field MJ, Fischer S, Gao J, Guo H, Ha S, Joseph-McCarthy D, Kuchnir L, Kuczera K, Lau FTK, Mattos C, Michnick S, Ngo T, Nguyen DT, Prodhom B, Reiher WE, Roux B, Schlenkrich M, Smith JC, Stote R, Straub J, Watanabe M, Wirkiewicz-Kuczera J, Yin D, Karplus M (1998) All-atom empirical potential for molecular modeling and dynamics studies of proteins. J Phys Chem B 102(18):3586–3616 [DOI] [PubMed] [Google Scholar]
  20. Martyna GJ, Tobias DJ, Klein ML (1994) Constant pressure molecular dynamics algorithms. J Chem Phys 101(5):4177–4189 [Google Scholar]
  21. Paliy M, Melnik R, Shapiro BA (2009) Molecular dynamics study of the RNA ring nanostructure: a phenomenon of self-stabilization. Phys Biol 6(4):046003. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Paliy M, Melnik R, Shapiro BA (2010) Coarse-graining RNA nanostructures for molecular dynamics simulations. Phys Biol 7(3):036001. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Phillips JC, Braun R, Wang W, Gumbart J, Tajkhorshid E, Villa E, Chipot C, Skeel RD, Kal L, Schulten K (2005) Scalable molecular dynamics with NAMD. J Comput Chem 26(16):1781–1802 [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Shu D, Shu Y, Haque F, Abdelmawla S, Guo P (2011) Thermodynamically stable RNA three-way junction for constructing multifunctional nanoparticles for delivery of therapeutics. Nat Nano 6(10):658–667 [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Shu Y, Cinier M, Fox SR, Ben-Johnathan N, Guo P (2011) Assembly of therapeutic pRNA-siRNA nanoparticles using bipartite approach. Mol Ther 19(7):1304–1311 [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Tomizawa JI (1984) Control of cole 1 plasmid replication: the process of binding of RNA I to the primer transcript. Cell 38(3):861–870 [DOI] [PubMed] [Google Scholar]
  27. Tomizawa JI (1986) Control of ColE1 plasmid replication: binding of RNA I to RNA II and inhibition of primer formation. Cell 47(1):89–97 [DOI] [PubMed] [Google Scholar]
  28. Vieregg J, Cheng W, Bustamante C, Tinoco I (2007) Measurement of the effect of monovalent cations on RNA hairpin stability. J Am Chem Soc 129(48):14966–14973 [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Yano J, Hirabayashi K, Nakagawa SI, Yamaguchi T, Nogawa M, Kashimori I, Naito H, Kitagawa H, Ishiyama K, Ohgi T, Irimura T (2004) Antitumor activity of small interfering RNA/cationic liposome complex in mouse models of cancer. Clin Cancer Res 10(22):7721–7726 [DOI] [PubMed] [Google Scholar]
  30. Yingling YG, Shapiro BA (2007) Computational design of an RNA hexagonal nanoring and an RNA nanotube. Nano Lett 7(8):2328–2334 [DOI] [PubMed] [Google Scholar]

RESOURCES