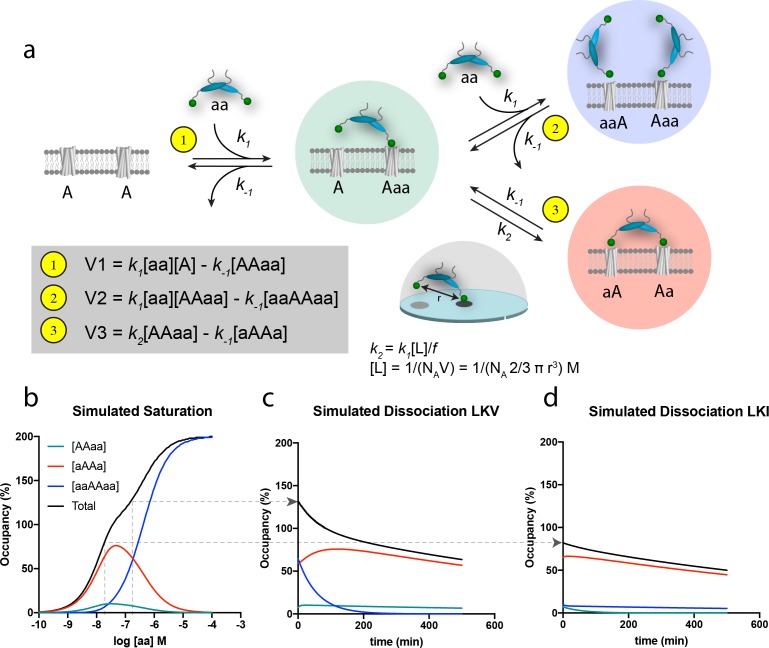
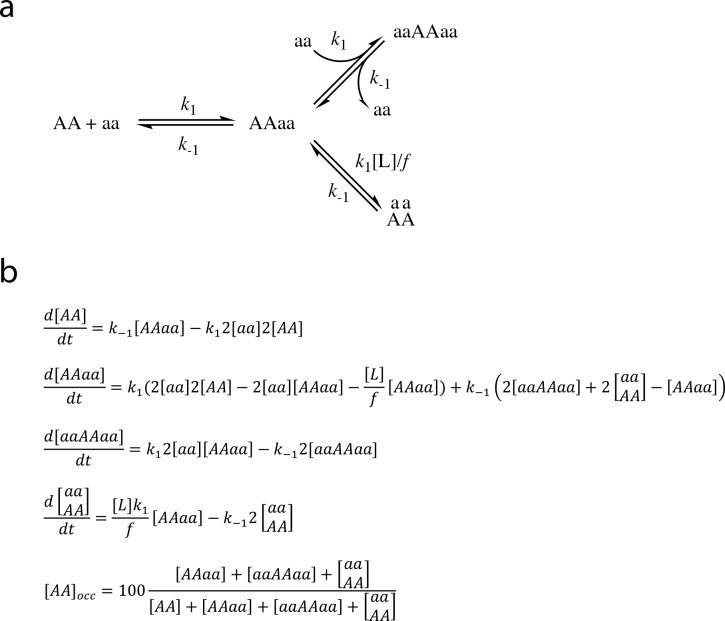
Figure 4. Schematic representation of the thermodynamic model for homobivalent ligand-target interactions and thereon-based simulated saturation and dissociation curves.

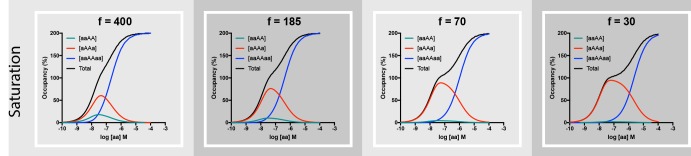
(a) Thermodynamic scheme for homobivalent ligand, ‘aa’- target, ‘AA’, interactions (see also Figure 4—figure supplement 1 for full scheme). The different binding modes in panel a are designated by ‘AAaa’ for the partially bound complexes (green), by ‘aAAa’ for the bivalently bound complex (red) and by ‘aaAAaa’ for ‘ternary’ complex with two partly bound ligands (blue). The rebinding kinetics is dependent the local concentration, [L], that is calculated as that of one molecule within a half-sphere with radius, r. Moreover, the rate constant is modified by f due to steric hindrance, restricted rational freedom and entropic cost. An f of 185 enables good qualitative simulation of our data (see also Figure 4—figure supplement 3 for behavior at other values of f). (b) Simulated saturation binding curve for binding of species. Input parameters: k₁ = 1.85⋅10⁵ M⁻¹min⁻¹, k_-1 = 0.0085 min-⁻¹, k₂ = 0.136 min⁻¹ (i.e. a composite rate constant such as defined in the figure). Total incubation time is 120 min. Analysis of the total signal according to a variable slope sigmoidal dose-response paradigm yields half-maximal signal at 50 nM. Note for these parameters the blue ‘ternary’ complex outpaces the red bivalent complex at bulk concentration of PICK1 above 100 nM. (c,d) Simulated dissociation curves after 120 min pre-incubation with 200 nM (c) and 20 nM (d) of the same homobivalent ligand as in panel c (corresponding to the affinity difference between LKV and LKI). [aa] is set and kept at 0 for simulating the ‘washout phase’.

Figure 4—figure supplement 1. Differential equations to follow the time-wise changes in the different target species shown in Figure 4.

(a) Abbreviated notation for the free and bound target species. As in Figure 4a, the different binding modes are designated by ‘AAaa’ for the partly complexes, by ‘aAAa’ for the fully bound bivalent complex and by ‘aaAAaa’ for the ternary complexes with two partly bound ligands. (b) Differential equations used for simulating the time-wise changes in the different target species. k₁ is the association and k_-1 the dissociation rate constants for the monovalent binding. When PICK1 is only attached via one of its PDZ domains the second PDZ domain can only move within half of a sphere with a radius, r, corresponding to the maximal distance between the two PDZ domains. The local concentration of the second PDZ domain, [L], can be calculated as showed in Figure 4a. The penalty factor, f, is introduced to modulate the association rate constant of the second PDZ interaction (k₂) in order to account for limited rotational freedom, sterical hinderance or structural rearrangements governing binding of the second PDZ domain. [AA]occ refers to the sum of all ligand-bound species and is expressed as percent of the total target population.

Figure 4—figure supplement 2. comparison of the PICK WT - LKV binding curves derived from experiments and the simulation.

(a) Representative binding curve derived from a single binding experiment of PICK1 WT to LKV. Here the biphasic behavior is not masked by the experimental error between different n’s and the biphasic curve binding becomes more pronounced. (b) Simulated binding curve of PICK1 WT binding to WT from Figure 4. (c) Overlay of the two fits shows good agreement between our experiment and simulation. Simulation parameters are given in the legend of Figure 4 and in the Materials and method section.

Figure 4—figure supplement 3. Broader range of f ratios and homobivalent ligand concentrations to illustrate the influence of this parameter on saturation profiles.

The binding model and the ligand-emitted (fluorescence) signal intensity of the different binding modes is outlined in the legend of Figure 4 and Figure 4—figure supplement 1. Input parameters are similar to those used in Figure 4: r = 180 Å, k₁ = 1.85⋅10⁵ M⁻¹min⁻¹, k_-1 = 0.0085 min-⁻¹, k₂ = 0.136 min⁻¹. Investigated f values are given on top of the panel. Total incubation time is 120 min. Curves move from nearly- sigmoidal to outspokenly biphasic when f decreases. This phenomenon illustrates the fact that even higher [aa] is required for V2 to exceed V3 as the f parameter decrease.