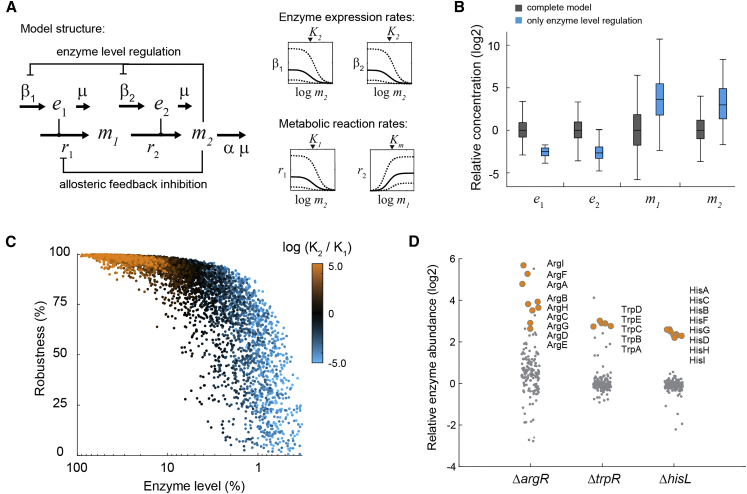
Figure 4.
A Kinetic Model Predicts a Robustness-Efficiency Tradeoff
(A) Stoichiometry and structure of the kinetic model. m1 and m2 are metabolites, e1 and e2 are enzymes. Kinetics of the enzyme catalyzed reactions r1 and r2, as well as kinetics of enzyme expression rates β1 and β2, are sampled in the indicated intervals.
(B) Steady-state concentrations of e1, e2, m1, and m2 calculated with 5,000 random parameter sets for the complete model (grey), and the model with only enzyme level regulation (blue). Boxes contain 50% and whiskers 99% of the simulated concentrations. All concentrations are normalized to the median concentrations of the complete model. See also Figures S6 and S7.
(C) Enzyme levels (sum of e1 and e2) and robustness against perturbations of β2,max for 5,000 simulations of the complete model (dots). The color of each dot shows the ratio of inhibition constants for allosteric feedback inhibition (K1) and enzyme level regulation (K2) in the respective model. Robustness corresponds to the percentage downregulation of β2,max that was tolerated by each model. 100% enzyme abundance corresponds to the maximum theoretical enzyme concentration in the model.
(D) Abundance of enzymes in amino acid metabolism in the ΔargR, ΔtrpR, and ΔhisL mutants, relative to the wild-type. Data are represented as mean (n = 3). For each strain the enzymes in the dysregulated pathway are shown as orange dots.