Skip to main content
PMC home page
Chemical Science logoLink to Chemical Science
. 2018 Nov 22;10(5):1466–1471. doi: 10.1039/c8sc04406f

Supramolecular cage encapsulation as a versatile tool for the experimental quantification of aromatic stacking interactions†

Carlo Bravin a, Giulia Licini a, Christopher A Hunter b, Cristiano Zonta a,✉
PMCID: PMC6354842  PMID: 30809364

graphic file with name c8sc04406f-ga.jpgA Double Mutant Cycle is built up using a supramolecular cage that binds two aromatic carboxylates in a stacked geometry is used to quantify aromatic stacking interactions.

Abstract

The widespread presence of aromatic stacking interactions in chemical and biological systems, combined with their relatively small energetic contribution, have led to a plethora of theoretical and experimental studies for their quantification and rationalization. Typically, π–π aromatic interactions are studied as a function of substituents to gather information about the interaction mechanism. While experiments suggest that aromatic interactions are dominated by local electrostatic contacts between π-electron density and CH groups, theoretical work has raised the possibility that direct electrostatic interactions between local dipoles of the substituents may play a role. We describe a supramolecular cage that binds two aromatic carboxylates in a stacked geometry such that the aromatic substituents are remote in space. Chemical Double Mutant Cycles (DMCs) were used to measure fifteen different aromatic stacking interactions as a function of substituent (NMe2, OMe, Me, Cl and NO2). When both aromatic rings have electron-withdrawing nitro substituents, the interaction is attractive (–2.8 kJ mol–1) due to reduced π-electron repulsion. When both aromatic rings have electron-donating di-methylamino substituents, the interaction is repulsive (+2.0 kJ mol–1) due to increased π-electron repulsion. The results show that aromatic stacking interactions are dominated by short range electrostatic contacts rather than substituent dipole interactions.

Introduction

Quantitative knowledge of the relationship between chemical structure and non-covalent interaction energies is fundamental in order to understand or design both structure and function in chemical and biological systems.1–15 Many research groups have focused their attention on the quantification of aromatic interactions using theoretical and experimental methods. Using a typical physical organic chemistry approach, the factors that govern these interactions have been studied by evaluating the influence of ring substitution on interaction energy.16–20 Solution phase experimental measurements indicate that aromatic interactions are dominated by the electrostatics of short range local contacts between π-electron density or CH–π interactions that depend on the geometry of interaction.21–25 Substituents affect the observed interaction energies by changing the π-electron density and the polarity of the peripheral CH groups. In contrast, most theoretical calculations have been carried out in the gas phase, where dispersion and long range electrostatics play a more important role.26–28 These computational studies suggest that electrostatic interactions between dipoles associated with the ring substituents may play a significant role.29–35 In the experimentally studied systems, the substituents are usually in close proximity, so it is difficult to dissect these contributions. Here we describe a new experimental system for quantifying aromatic interactions that allows this distinction to be made, because the substituents are not in direct contact.

We have previously used modified tris(pyridylmethyl)amine (TPMA) metal complexes and imine Dynamic Covalent Chemistry (DCC),36–38 to obtain a variety of supramolecular architectures.39–43 The supramolecular cage 1 shown in Scheme 1 demonstrates particularly interesting molecular recognition properties with respect to dicarboxylate guests.44,45 Here we report the interaction of this cage with monocarboxylate guests and show that these complexes provide a versatile experimental platform for the quantitative determination of substituent effects on aromatic stacking interactions. The results show that for a system where there is no direct contact between the substituents on the aromatic rings, aromatic stacking interactions are dominated by local electrostatic contacts between the π-systems rather than substituent dipole interactions.

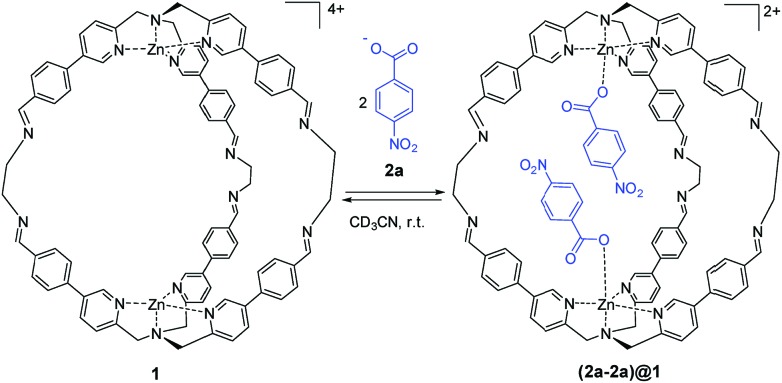
Scheme 1. Molecular recognition of 4-nitrobenzoate 2a by cage 1. Counterions are perchlorate for the cage and triethyl ammonium for the guest and they are omitted for clarity.

Scheme 1

Open in a new tab

Results and discussions

As reported in our previous work, supramolecular cage 1 was synthesized taking advantage of DCC. The initial aim of this work was to assess the molecular recognition properties of cage 1 towards aromatic carboxylate guests (Scheme 1).47

Sub-stoichiometric addition of 4-nitrobenzoate 2a to cage 1 in acetonitrile lead to the appearance of new signals in the 1H NMR spectrum that were in slow exchange with the signals due to the free cage (Fig. S1 in the ESI†). Integration of the bound cage and guest signals indicate exclusive formation of the cage–guest complex 1 : 2 (2a-2a)@1, and interestingly, no signals due to the 1 : 1 complex were detected.48 From the integrals of the free and bound 1H NMR signals, the overall equilibrium constant for formation of the 1 : 2 complex (K1K2) was determined (42 ± 4) × 106 M–2. The addition of more than two equivalents of 2a led to a complete conversion to the filled cage (2a-2a)@1 (Fig. S1 in the ESI†). The formation of the 1 : 2 complex (2a-2a)@1 was also confirmed by two-dimensional NMR spectroscopy (ROESY, DOSY) and ESI-MS experiments (Fig. S12–S15, ESI,†).

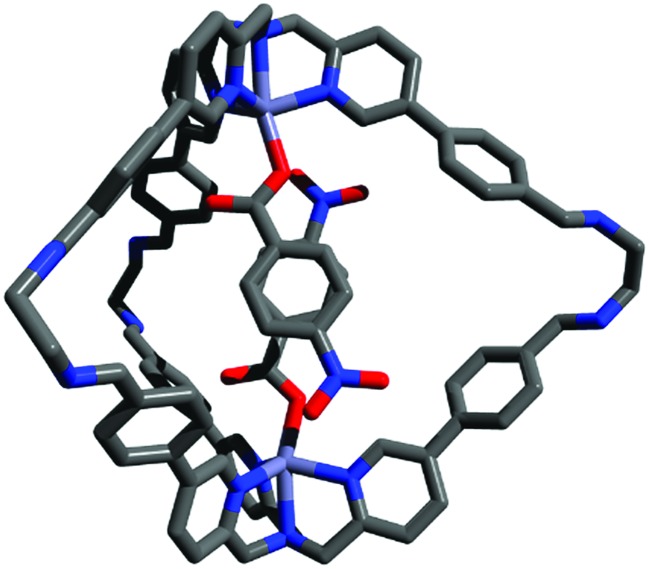
In order to gather structural information on (2a-2a)@1, DFT calculations were carried out. In the most stable conformation, the two guest aromatic rings adopt a face-to-face geometry with the nitro substituents in a pseudo-meta orientation (Fig. 1). The structure of the inclusion complex shown in Fig. 1 appears ideally suited for the determination of the thermodynamic properties of aromatic stacking interactions between the two guests. It is worth noting that in this structure the two nitro substituents are remote in space, so direct interactions between the substituents cannot affect the measured strength of the aromatic interaction. In addition, the two substituents are not parallel, so long range dipole interactions are also minimised relative to local contacts between the π-systems.46

Fig. 1. Representation of (2a-2a)@1 DFT (WB97XD/6-31G(d)) minimized structure. The aromatic rings of the two guests stack with one another, and the nitro substituents are directed to opposite sides of the cage cavity.

Fig. 1

Open in a new tab

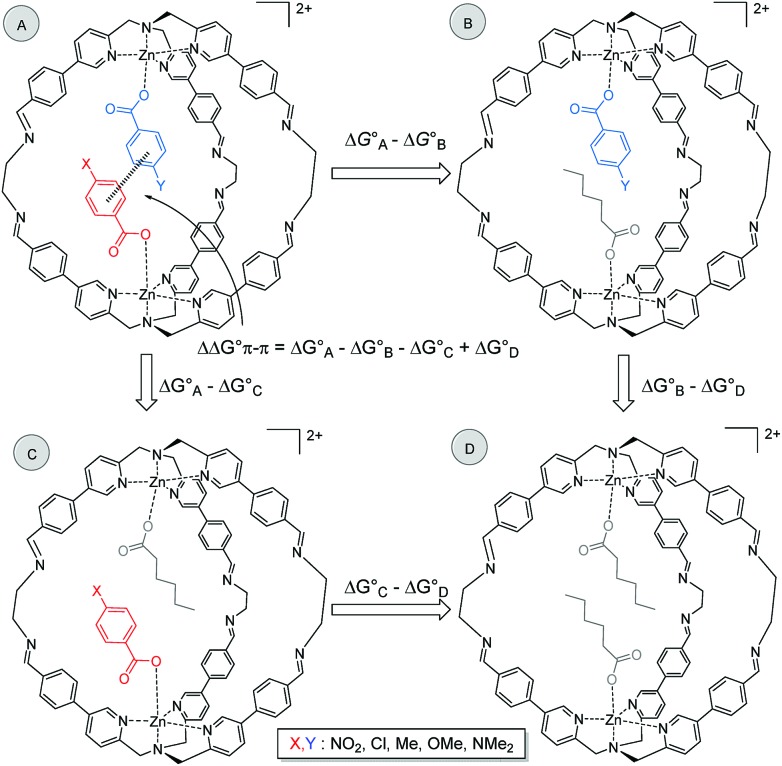
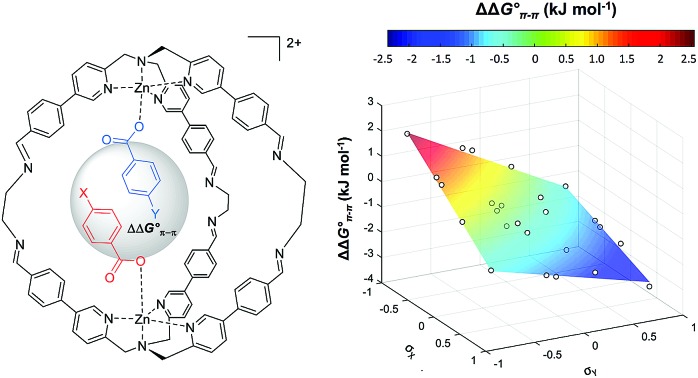
It is possible to dissect out the thermodynamic contribution of the aromatic stacking interaction from all of the other contributions in this system by the chemical Double Mutant Cycle (DMC) approach, which has been used to quantify non-covalent interactions in different systems.49,50 We used n-hexanoate HexA as a reference guest that cannot make aromatic interactions. The approach is illustrated for two different guests with substituents X and Y in Fig. 2 (see Section S3.5). There are a large number of different intermolecular interactions in Complex A which contains the aromatic stacking interaction of interest:

Fig. 2. Chemical DMC for measuring the aromatic stacking interaction between two guests. Counterions are perchlorate for the cage and triethyl ammonium for the guest and they are omitted for clarity.

Fig. 2

Open in a new tab

(1) The aromatic stacking interaction between the two guests.

(2) The coordination interaction between the carboxylate group of the guest with substituent X and the zinc ion.

(3) The coordination interaction between the carboxylate group of the guest with substituent Y and the zinc ion.

(4) Interactions of the edges of the aromatic ring with substituent X with the internal walls of the cage.

(5) Interactions of the edges of the aromatic ring with substituent Y with the internal walls of the cage.

(6) Interactions of substituent X with the walls of the cage.

(7) Interactions of substituent Y with the walls of the cage.

(8) Interactions between the carboxylate group of one guest and substituent X on the other guest.

(9) Interactions between the carboxylate group of one guest and substituent Y on the other guest.

Complex A contains all 9 types of interaction listed above. Complex B is missing interactions 4, 6 and 8. Thus the difference between the stabilities of complexes A and B 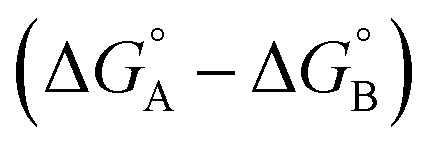Inline graphic measures the sum of interactions 1, 3, 5, 7 and 9 plus the difference in the strength of zinc–carboxylate coordination bond formed with the aromatic guest with substituent X and the aliphatic guest.

Similarly, Complex C is missing interactions 5, 7 and 9, and Complex D is missing interactions 4, 5, 6, 7, 8 and 9. Thus the difference between the stabilities of complexes C and D 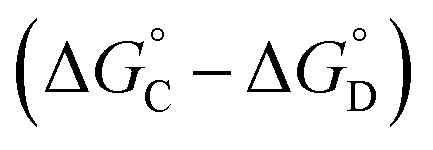Inline graphic measures the sum of interactions 4, 6 and 8 plus the difference in the strength of zinc–carboxylate coordination bonds formed with the aromatic guest with substituent X and the aliphatic guest. In other words, the only contribution to the difference 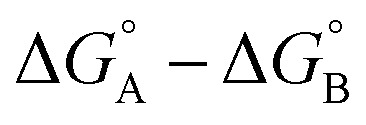Inline graphic that is not present in the difference 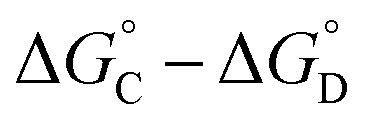Inline graphic is interaction 1, the aromatic stacking interaction.

Thus the DMC in Fig. 2 allows direct determination of the thermodynamic contribution due to the aromatic stacking interaction and removes all of the contributions from the many secondary interactions that are present in this system. Moreover, the DMC analysis is based on the differences in free energies between pairs of complexes, so it is not necessary to measure individual association constants for all 4 complexes shown in Fig. 2. Relative rather than absolute values are all that is required.

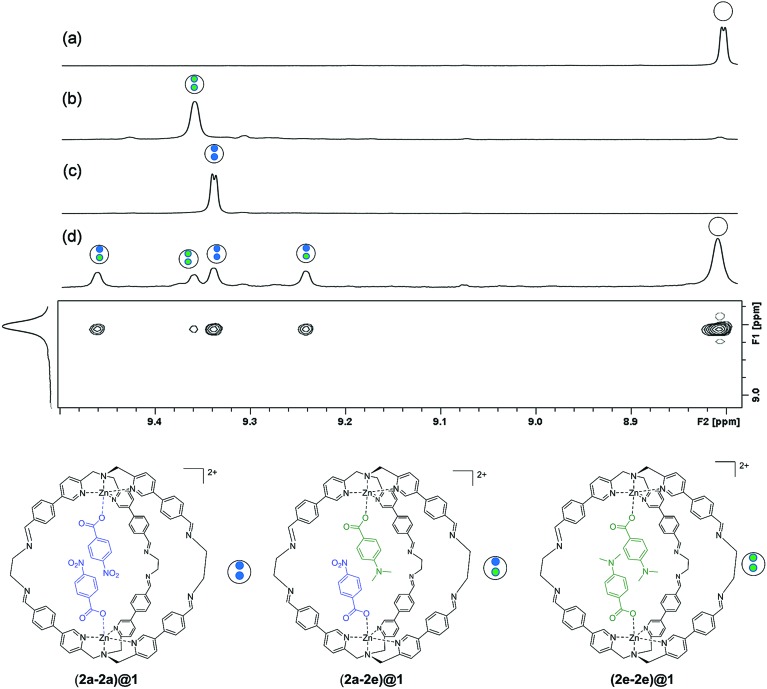
In order for this experiment to work, two guests must be bound in the same cage. We therefore chose 4-chlorobenzoate 2b, 4-methylbenzoate 2c, 4-methoxybenzoate 2d and 4-(dimethylamino)benzoate 2e (Fig. 2), which have similarly sized substituents to 4-nitrobenzoate 2a and should not introduce steric clashes with the cage walls. Fig. 3d illustrates typical results obtained using two different guests that form a mixed cage complex (2a-2e)@1. When 0.1 equivalents of carboxylate 2a and 0.1 equivalents of carboxylate 2e were added to a solution of cage 1 in acetonitrile, four new signals due to the cage pyridine α protons were observed (Fig. 3d). Comparison with the chemical shifts of the homo occupied cages allowed assignment of two of the signals to complexes containing the same guest (9.375 ppm for (2a-2a)@1 and 9.395 ppm for (2e-2e)@1) (Fig. 3b and c). In this case no ROESY cross-peaks between these signals are detected (Section S3.3 in the ESI†). The other two signals were assigned to the complex containing two different guests (2a-2e)@1 thanks to ROESY cross peak correlations (Fig. 3 and ESI† Section S3.3).

Fig. 3. Partial 500 MHz 1H NMR spectra showing the signals due to the cage pyridine α protons (301 K, CD3CN) for (a) cage 1 (b) (2e-2e)@1 (c) (2a-2a)@1 and (d) 1H ROESY experiment for the competition experiment between guest 2a and 2e ([1] = 1.0 mM, [2a] = [2e] = 0.1 mM). Counterions are perchlorate for the cage and triethyl ammonium for the guest and they are omitted for clarity.

Fig. 3

Open in a new tab

Integration of the signals related to the filled cages and the corresponding signal due to the empty cage 1 (8.015 ppm) allowed direct determination of the equilibrium constants for formation of (2a-2a)@1, (2e-2e)@1 and (2a-2e)@1.

In other words, if two different guests are present in sub-stoichiometric amounts, due to the slow exchange on the 1H NMR timescale it is possible to measure all three equilibrium constants for formation of the hetero- and the two homo-complexes with a single NMR acquisition (Section S3.4 in the ESI†). Using this approach, equilibrium constants were measured for all pairwise combinations of carboxylate guests (2a–2e and HexA). With these values, it was possible to construct fifteen different DMCs to measure the free energy contributions of fifteen different aromatic stacking interactions to the overall stabilities of the complexes (ΔΔG°), (Table S1–S5 and Fig. S5 and S6 in the ESI†) (Table 1).

Table 1. Free energy contributions (ΔΔG° in kJ mol–1) from aromatic stacking interactions measured using DMCs.

Y X
NO2 Cl Me OMe NMe2
NO2 –2.8 ± 0.1
Cl –2.1 ± 0.3 –1.7 ± 0.1
Me –1.9 ± 0.2 –1.0 ± 0.1 –0.9 ± 0.1
OMe –1.8 ± 0.1 –0.5 ± 0.3 –0.5 ± 0.1 0.0 ± 0.2
NMe2 –1.2 ± 0.1 –0.1 ± 0.2 +0.8 ± 0.2 +1.0 ± 0.1 +2.0 ± 0.3
Open in a new tab

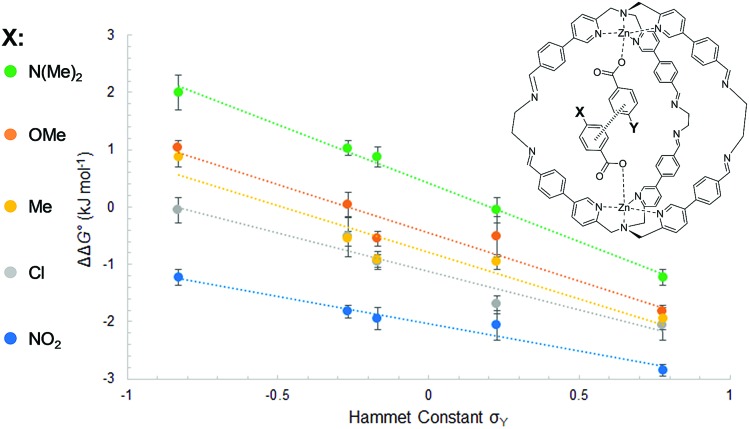
The least favorable interaction occurs when both aromatic rings carry electron-donating dimethylamino groups (+2.0 ± 0.4 kJ mol–1), and the most attractive interaction occurs when both aromatic rings carry electron-withdrawing nitro groups (–2.8 ± 0.1 kJ mol–1). The measured aromatic interaction energies are in line with the previously reported experimental measurements and correlate well with the corresponding Hammett substituent parameters (Fig. 4) and the electrostatic potential of the substituted aromatic rings (Section S3.6).16,17

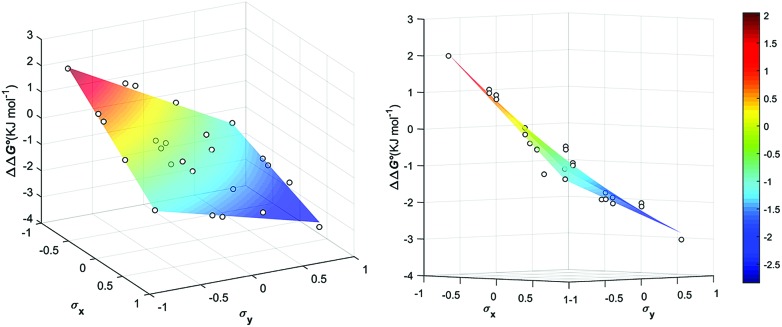
ΔΔG° (kJ mol–1) = 0.7 σxσy – 1.5σx – 1.5σy – 0.9 1

When X = NMe2, a linear Hammett correlation is observed for all five Y substituents with a slope of –2.0 kJ mol–1. As X becomes less electron-donating, the correlation remains linear, but the slope decreases, down to a value of –0.9 kJ mol–1 for X = NO2. The slopes and intercepts of the linear correlations shown in Fig. 5 also correlate with the Hammett substituents parameters for X (Fig S9 and S10 in the ESI†), so it is possible to describe the entire dataset by eqn (1). Eqn (1) is plotted as a 3D graph in Fig. 5 demonstrating the excellent correlation with the experimental values.

Fig. 4. Aromatic stacking energies (kJ mol–1) measured for the guest with substituent X (y-axis) plotted as a function of the Hammet constant σY of the guest with substituent Y (x-axis). The slope and the R2 for each substituent are respectively NMe2 (ρ = –2.0, R2 = 0.96); OMe (ρ = –1.7, R2 = 0.99); Me (ρ = –1.6, R2 = 0.91); Cl (ρ = –1.3, R2 = 0.94); NO2 (ρ = –1.0, R2 = 0.96).

Fig. 4

Open in a new tab

Fig. 5. Aromatic stacking energies (kJ mol–1) (z-axis) measured as function of the Hammet constant σY and σY of the encapsulated guests.

Fig. 5

Open in a new tab

Conclusions

In conclusion, both the trends in interaction energy with substituent and the absolute values of the free energies of interaction are very similar to previously reported experimental measurements of aromatic interactions in different systems.16,17 However, the orientation of the substituents in the system reported here (approximately orthogonal) is quite different from the orientation of the aromatic substituents in previous studies (approximately parallel). This observation indicates that aromatic stacking interactions are dominated by short range local electrostatic interactions between the π-faces rather than by substituent dipole interactions.32 In particular, the cage fixes the orientation of the guests in such a way that the polarizing aromatic substituents are not in contact, which means that there are no contributions from direct interactions between the substituents. Moreover the substituents are not parallel, so long range dipole interactions are minimised. The finding that local electrostatic interactions dominate is in line with previous solution phase experimental studies and contradicts ideas based on gas phase theoretical calculations.31,32 The 1 : 2 cage–guest complexes represent a powerful system for the quantification of non-covalent interactions using the DMC approach and provide a versatile platform for controlling assembly and molecular recognition within the supramolecular superstructure.

Conflicts of interest

There are no conflicts to declare.

Supplementary Material

Click here for additional data file. (3.1MB, pdf)

Acknowledgments

The authors would like to thank Prof. J. K. Sanders and C. Berton for useful discussions. Financial support from the University of Padova (PRAT-CPDA153122, Progetto Attrezzature Scientifiche finalizzate alla Ricerca) is gratefully acknowledged.

Footnotes

†Electronic supplementary information (ESI) available: Experimental details on the competition experiments, DMCs and characterization of all new compounds. See DOI: 10.1039/c8sc04406f

References

  1. Hunter C. A., Sanders J. K. M. J. Am. Chem. Soc. 1990;112:5525–5534. [Google Scholar]
  2. Meyer A. E., Castellano K. R., Diederich F. Angew. Chem., Int. Ed. 2003;42:1210–1250. doi: 10.1002/anie.200390319. [DOI] [PubMed] [Google Scholar]
  3. Salonen M. L., Ellermann M., Diederich F. Angew. Chem., Int. Ed. 2011;50:4808–4842. doi: 10.1002/anie.201007560. [DOI] [PubMed] [Google Scholar]
  4. Cockroft S. L., Hunter C. A. Chem. Commun. 2006:3806–3808. doi: 10.1039/b608165g. [DOI] [PubMed] [Google Scholar]
  5. Núñez-Villanueva D., Iadevaia G., Stross A. E., Jinks M. A., Swain J. A., Hunter C. A. J. Am. Chem. Soc. 2017;139:6654–6662. doi: 10.1021/jacs.7b01357. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Hunter C. A., Lawson K. R., Perkins J., Urch C. J. J. Chem. Soc., Perkin Trans. 2. 2001:651–669. [Google Scholar]
  7. Yoshizawa M., Tamura M., Fujita M. Science. 2006;312:251–254. doi: 10.1126/science.1124985. [DOI] [PubMed] [Google Scholar]
  8. Hunter C. A. Angew. Chem., Int. Ed. 2004;43:5310–5324. doi: 10.1002/anie.200301739. [DOI] [PubMed] [Google Scholar]
  9. Ronson T. K., Meng W., Nitschke J. R. J. Am. Chem. Soc. 2017;139:9698–9707. doi: 10.1021/jacs.7b05202. [DOI] [PubMed] [Google Scholar]
  10. Harder M., Carnero Corrales M. A., Trapp N., Kuhn B., Diederich F. Chem.–Eur. J. 2015;21:8455–8463. doi: 10.1002/chem.201500462. [DOI] [PubMed] [Google Scholar]
  11. Biedermann F., Schneider H.-J. Chem. Rev. 2016;116:5216–5300. doi: 10.1021/acs.chemrev.5b00583. [DOI] [PubMed] [Google Scholar]
  12. Bhayana B. J. Org. Chem. 2013;78:6758–6762. doi: 10.1021/jo400782e. [DOI] [PubMed] [Google Scholar]
  13. Kim E., Paliwal S., Wilcox C. S. J. Am. Chem. Soc. 1998;120:11192–11193. [Google Scholar]
  14. Newcomb L. F., Gellman S. H. J. Am. Chem. Soc. 1994;116:4993–4994. [Google Scholar]
  15. Rashkin M. J., Waters M. L. J. Am. Chem. Soc. 2002;124:1860–1861. doi: 10.1021/ja016508z. [DOI] [PubMed] [Google Scholar]
  16. Cockroft S. L., Hunter C. A., Lawson K. R., Perkins J., Urch C. J. J. Am. Chem. Soc. 2005;127:8594–8595. doi: 10.1021/ja050880n. [DOI] [PubMed] [Google Scholar]
  17. Cockroft S. L., Perkins J., Zonta C., Adams H., Spey S. E., Low C. M. R., Vinter J. G., Lawson K. R., Urch C. J., Hunter C. A. Org. Biomol. Chem. 2007;5:1062–1080. doi: 10.1039/b617576g. [DOI] [PubMed] [Google Scholar]
  18. Riwar L.-J., Trapp N., Kuhn B., Diederich F. Angew. Chem., Int. Ed. 2017;56:11252–11257. doi: 10.1002/anie.201703744. [DOI] [PubMed] [Google Scholar]
  19. Cozzi F., Cinquini M., Annuziata R., Siegel J. S. J. Am. Chem. Soc. 1993;115:5330–5331. [Google Scholar]
  20. Hwang J., Li P., Smith M. D., Shimizu K. D. Angew. Chem., Int. Ed. 2016;55:8086–8089. doi: 10.1002/anie.201602752. [DOI] [PubMed] [Google Scholar]
  21. Santoni G., Mba M., Bonchio M., Nugent W. A., Zonta C., Licini G. Chem.–Eur. J. 2010;16:645–654. doi: 10.1002/chem.200902072. [DOI] [PubMed] [Google Scholar]
  22. Carver F. J., Hunter C. A., Livingstone D. J., McCabe J. F., Seward E. M. Chem.–Eur. J. 2002;8:2847–2859. doi: 10.1002/1521-3765(20020703)8:13<2847::aid-chem2847>3.0.co;2-m. [DOI] [PubMed] [Google Scholar]
  23. Hunter C. A., Low C. M. R., Rotger C., Vinter J. G., Zonta C. Proc. Natl. Acad. Sci. U. S. A. 2002;99:4873–4876. doi: 10.1073/pnas.072647899. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Adams H., Hunter C. A., Lawson K. R., Perkins J., Spey S. E., Urch C. J., Sanderson J. M. Chem.–Eur. J. 2001;7:4863–4877. doi: 10.1002/1521-3765(20011119)7:22<4863::aid-chem4863>3.0.co;2-3. [DOI] [PubMed] [Google Scholar]
  25. Hunter C. A., Low C. M. R., Rotger C., Vinter J. G., Zonta C. Chem. Commun. 2003;3:834–835. doi: 10.1039/b300693j. [DOI] [PubMed] [Google Scholar]
  26. Yang L., Brazier J. B., Hubbard T. A., Rogers D. M., Cockroft S. L. Angew. Chem., Int. Ed. 2016;55:912–916. doi: 10.1002/anie.201508056. [DOI] [PubMed] [Google Scholar]
  27. Yang L., Adam C., Nichol G. S., Cockroft S. L. Nat. Chem. 2013;5:1006–1010. doi: 10.1038/nchem.1779. [DOI] [PubMed] [Google Scholar]
  28. wun Hwang J., Li P., Shimizu K. D. Org. Biomol. Chem. 2017;15:1554–1564. doi: 10.1039/c6ob01985d. [DOI] [PubMed] [Google Scholar]
  29. Wheeler S. E., Houk K. N. J. Am. Chem. Soc. 2008;130:10854–10855. doi: 10.1021/ja802849j. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Parrish R. M., Sherrill C. D. J. Am. Chem. Soc. 2014;136:17386–17389. doi: 10.1021/ja5101245. [DOI] [PubMed] [Google Scholar]
  31. Wheeler S. E. Acc. Chem. Res. 2013;46:1029–1038. doi: 10.1021/ar300109n. [DOI] [PubMed] [Google Scholar]
  32. Wheeler S. E. J. Am. Chem. Soc. 2011;133:10262–10274. doi: 10.1021/ja202932e. [DOI] [PubMed] [Google Scholar]
  33. Hwang J., Li P., Carroll W. R., Smith M. D., Pellechia P. J., Shimizu K. D. J. Am. Chem. Soc. 2014;136:14060–14067. doi: 10.1021/ja504378p. [DOI] [PubMed] [Google Scholar]
  34. Hwang J., Dial B. E., Li P., Kozik M. E., Smith M. D., Shimizu K. D. Chem. Sci. 2015;6:4358–4364. doi: 10.1039/c5sc01370d. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Maier J. M., Li P., Vik E. C., Yehl C. J., Strickland S. M. S., Shimizu K. D. J. Am. Chem. Soc. 2017;139:6550–6553. doi: 10.1021/jacs.7b02349. [DOI] [PubMed] [Google Scholar]
  36. Corbett P. T., Leclaire J., Vial L., West K. R., Wietor J.-L., Sanders J. K. M., Otto S. Chem. Rev. 2006;106:3652–3711. doi: 10.1021/cr020452p. [DOI] [PubMed] [Google Scholar]
  37. Black S. P., Wood D. M., Schwarz F. B., Ronson T. K., Holstein J. J., Stefankiewicz A. R., Schalley C. A., Sanders J. K. M., Nitschke J. R. Chem. Sci. 2016;7:2614–2620. doi: 10.1039/c5sc04906g. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Castilla A. M., Ronson T. K., Nitschke J. R. J. Am. Chem. Soc. 2016;138:2342–2351. doi: 10.1021/jacs.5b13016. [DOI] [PubMed] [Google Scholar]
  39. Berardozzi R., Badetti E., Carmo dos Santos N. A., Wurst K., Licini G., Pescitelli G., Zonta C., Di Bari L. Chem. Commun. 2016;52:8428–8431. doi: 10.1039/c6cc04167a. [DOI] [PubMed] [Google Scholar]
  40. Badetti E., Wurst K., Licini G., Zonta C. Chem.–Eur. J. 2016;22:6515–6518. doi: 10.1002/chem.201600480. [DOI] [PubMed] [Google Scholar]
  41. Scaramuzzo F. A., Badetti E., Licini G., Zonta C. Eur. J. Org. Chem. 2017;2017:1438–1442. [Google Scholar]
  42. Scaramuzzo F. A., Licini G., Zonta C. Chem.–Eur. J. 2013;19:16809–16813. doi: 10.1002/chem.201302721. [DOI] [PubMed] [Google Scholar]
  43. Badetti E., Dos Santos N. A. C., Scaramuzzo F. A., Bravin C., Wurst K., Licini G., Zonta C. RSC Adv. 2018;8:19494–19498. doi: 10.1039/c8ra03989e. [DOI] [PMC free article] [PubMed] [Google Scholar]
  44. Bravin C., Badetti E., Scaramuzzo F. A., Licini G., Zonta C. J. Am. Chem. Soc. 2017;139:6456–6460. doi: 10.1021/jacs.7b02341. [DOI] [PubMed] [Google Scholar]
  45. Bravin C., Badetti C., Putreddy E., Pan R., Rissanen F., Licini K., Zonta G. Chem.–Eur. J. 2018;24:2936–2943. doi: 10.1002/chem.201704725. [DOI] [PubMed] [Google Scholar]
  46. Carver F. J., Hunter C. A., Carver F. J., Seward E. M. Chem. Commun. 1998:775–776. [Google Scholar]
  47. Embedded ethylenediamine and the molecular recognition process of cage 1 towards dicarboxylic acid was clarified in ref. 44
  48. Cage : mono-carboxylate 1 : 1 complex formation was noticed only for the encapsulation of lower affinity mono carboxylate viz.HexA, (ESI Section S3.2)
  49. Cockroft S. L., Hunter C. A. Chem. Soc. Rev. 2007;36:172–188. doi: 10.1039/b603842p. [DOI] [PubMed] [Google Scholar]
  50. Hunter C. A., Low C. M. R., Vinter J. G., Zonta C. J. Am. Chem. Soc. 2003;125:9936–9937. doi: 10.1021/ja034767d. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Click here for additional data file. (3.1MB, pdf)

Articles from Chemical Science are provided here courtesy of Royal Society of Chemistry

RESOURCES