Typical physics Ph.D. admissions criteria limit access to underrepresented groups but fail to predict doctoral completion

Graduate admissions tests cannot identify the students most likely to complete a Ph.D. in physics.

Abstract

This study aims to understand the effectiveness of typical admissions criteria in identifying students who will complete the Physics Ph.D. Multivariate statistical analysis of roughly one in eight physics Ph.D. students from 2000 to 2010 indicates that the traditional admissions metrics of undergraduate grade point average (GPA) and the Graduate Record Examination (GRE) Quantitative, Verbal, and Physics Subject Tests do not predict completion as effectively admissions committees presume. Significant associations with completion were found for undergraduate GPA in all models and for GRE Quantitative in two of four studied models; GRE Physics and GRE Verbal were not significant in any model. It is notable that completion changed by less than 10% for U.S. physics major test takers scoring in the 10th versus 90th percentile on the Quantitative test. Aside from these limitations in predicting Ph.D. completion overall, overreliance on GRE scores in admissions processes also selects against underrepresented groups.

INTRODUCTION

Physics is the least diverse of the sciences, rivaling mechanical engineering and aerospace engineering for the least diverse fields within all of science, technology, mathematics, and engineering (STEM) (1). Groups underrepresented in physics include Blacks, Latinos, Native Americans, and women of all racial/ethnic groups. Barely 5% of physics Ph.D.’s are granted annually to those identifying with an underrepresented racial/ethnic category; women earn only 20% of physics Ph.D.’s. The origins of these vast representation gaps are complex and include inequitable educational access from an early age (2), implicit bias in the classroom and research laboratories (3), deterrents to continuation for underrepresented groups (e.g., departmental climate and disciplinary culture) (4–6), and stereotype threat (7, 8). Expanding gender and racial participation in STEM is important for the development of a robust domestic scientific workforce, however, as pointed out by the National Academy of Sciences report Expanding Underrepresented Minority Participation: America’s Science and Technology Talent at the Crossroads (9). Who gets to do the science of the future is determined largely by who is selected into Ph.D. programs. Transition of students to graduate work is thus a concern of national importance; only by attending to structural issues present in the process of selecting who gets to do the science of the future can we make sustainable progress toward broadening the participation of groups historically underrepresented in STEM.

Unfortunately, nontrivial barriers impede admission to Ph.D. programs for some demographic groups. Undergraduate grades, college selectivity, and GRE scores are the three criteria that best predict admission to U.S. graduate programs (10), but these parameters are not evenly distributed by race and gender (10, 11). This situation is particularly problematic for easily sortable numeric metrics, such as GRE scores. Predictive validity analyses of the GRE are almost as old as the test itself (12–14). Research over decades of test refinement, as well as meta-analysis of this research, consistently finds that scores on the Verbal and Quantitative GRE (GRE-V and GRE-Q, respectively) have weaker validity for Ph.D. attainment than for graduate school grades (15). Using the same database as (15), additional analysis identified positive relationships between these tests’ scores and first-year grades, cumulative grades, and faculty ratings (16). In a similar vein, two recent studies on biomedical Ph.D. admissions found that the General GRE does not predict scholarly productivity (17) or degree completion but that scores are associated with first-semester and cumulative graduate school grades (18). Methodologically, most assessments of validity focus on the general test and are limited to bivariate correlation analyses; they do not include covariates to render more precise estimates. Overall, the record indicates that the GRE’s validity wanes as time elapses between taking the test and measuring “success” in graduate school, which may be indicated by completion, research productivity, and other markers of success.

Despite their near-universal employment by physics Ph.D. programs (19), no study has tested the validity of common admissions metrics explicitly in these programs. Given the strong race, gender, and citizenship performance differences on the GREs in particular (10, 11), it is critical that we know the extent to which scores are useful in identifying students who will complete the Ph.D. We conducted such a study, inviting physics programs to submit de-identified student admission and degree completion records. Among applicants who were admitted and matriculated into physics Ph.D. programs, we find the predictive validity to be poor for some of the most ubiquitously used admissions criteria. In particular, we find undergraduate GPA (UGPA) to be the most robust numerical predictor of Ph.D. completion, and, despite a large sample size and wide dynamic range, we do not find a statistically significant relationship between GRE Physics (GRE-P) Subject Test scores and Ph.D. completion.

This article is structured as follows. First, we provide a snapshot of the state of U.S. physics with respect to diversity and degree production. Next, we describe U.S. citizens’ performance on the GRE-P across a variety of demographic parameters. We then describe our multivariate regression analysis and its findings. Last, we conclude with implications of these results.

Current state of U.S. physics

The state of diversity in physics can be summarized by the annual average numbers of bachelor’s degrees awarded, first year graduate students, Ph.D.’s awarded, and the performance of students on the GRE-P. Whereas the latter data are obtained from ETS itself, the remainder are available through the Integrated Postsecondary Education Data System (IPEDS) (20). From the IPEDS data (Table 1), several observations are possible. At all stages of physics education, Latinos and Blacks are underrepresented relative to their college-age representation in the United States, whereas Asians and Whites are overrepresented. The ratio of GRE-P test takers to physics undergraduate degrees awarded indicates that approximately half of physics undergraduate degree earners are actively considering physics graduate studies. About one quarter of U.S. physics majors matriculate into U.S. physics graduate programs. Significant exceptions to these trends are noted for Blacks, who take the GRE-P and matriculate at lower rates than the national average. Black females, Latinas, and Native Americans of any gender each had fewer than 10 physics Ph.D. matriculants annually in these data. Women are barely 20% of physics students, at both the undergraduate and graduate levels, and they take the GRE-P in proportion to their representation.

Table 1. Multiyear averages for diversity metrics in U.S. physics.

Each row’s entries show the percentage of the U.S. annual average in the second column. Data for the GRE-P are the average over test years 2009–2015; all others are the averages from 2009–2014 (20). We excluded data if an entry’s absolute number was 10 or less (indicated by asterisks) and excluded race categories “other,” “two or more,” and “no response.” F, female; M, male.

	U.S. annual	U.S.		Hispanic		Asian		Black		White		Native American		Non-U.S.
	Average	F	M	F	M	F	M	F	M	F	M	F	M	F	M
Baccalaureate degrees	5837	19%	81%	1.2%	5.0%	1.6%	5.5%	0.7%	2.1%	14%	61%	*	0.4%	–	–
GRE-P test takers	2914	20%	80%	1.2%	4.3%	1.9%	6.3%	0.4%	1.3%	16%	63%	*	0.4%	570	2073
Ph.D. matriculants	1550	18%	82%	1.0%	4.8%	1.4%	5.2%	*	1.6%	14%	63%	*	*	266	897
Ph.D.’s awarded	960	18%	82%	*	3.5%	2.0%	5.5%	*	1.6%	13%	61%	*	*	182	681
GRE-P test takers per baccalaureate degree	50%	52%	49%	51%	43%	57%	57%	26%	30%	55%	51%	*	42%	–	–
Ph.D. matriculants per baccalaureate degree	27%	25%	27%	23%	25%	23%	25%	*	20%	26%	27%	*	*	–	–
Ph.D. completion rate	62%	62%	62%	*	46%	86%	65%	*	60%	59%	60%	*	*	68%	76%

IPEDS data indicate that around 60% of U.S. citizens who matriculate to Ph.D. programs will complete their degree. We do not take into consideration the time dependence of matriculants and Ph.D.’s earned, leading to some ambiguity in completion rate. However, we note that the Council of Graduate Schools indicates that the 10-year completion rate for physics overall is 59%, close to what we report here (21). There is no overall gender gap for physics Ph.D. completion or time to Ph.D. among U.S. citizen graduate students. With the caveat that low enrollment numbers imply a relative error on the order of 20%, these data indicate that Hispanic males have a lower Ph.D. completion rate than the average and that Asian females have the highest Ph.D. completion rate of U.S. citizens (Table 1).

Figure 1 shows significant gaps in GRE-P scores for U.S. citizens based on race and gender. These data, obtained from the ETS database (portal.ets.org), represent all test takers who earned a valid GRE-P score in test years 2009–2015. The median U.S. female score is 580 (28th percentile), while the median U.S. male score is 650 (46th percentile); ETS reports (22) the SE of measurement to be 49 points (roughly 9th percentile), indicating that gender gaps are statistically significant. Notably, similarly large gender gaps in GRE-P scores exist for all racial/ethnic groups for both U.S. and international test takers [median percentile by country for (male, female) test takers were as follows: China (86th, 77th), India (70th, 46th), and Iran (62nd, 42nd)]. The median scores for Black (530; 17th percentile), Hispanic (580; 28th percentile), White (630; 39th percentile), and Asian Americans (690; 53rd percentile) also reveal significant variation in GRE-P by race.

Fig. 1. The fraction of U.S. test takers above a specified GRE-P score shows that cutoff scores adversely affect underrepresented groups more than majority groups.

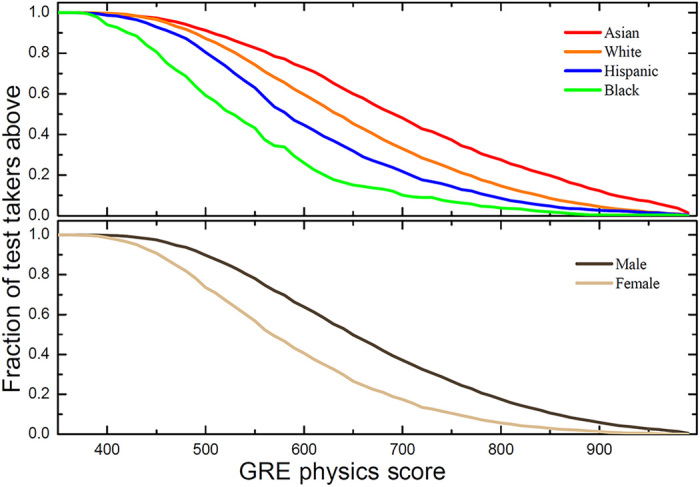
Given that we find that Ph.D. completion is not correlated with the GRE-P score, the misuse of the test in admissions will negatively affect diversity without being able to identify individuals able to complete a physics Ph.D. Source: ETS.

Although the best evidence suggests that faculty are well intentioned when selecting students, many are unaware of demographic patterns in GRE scores and they carry out admissions according to inherited practices that include using cutoff scores (23). Programs using the GRE-P as an integral part of their admissions process may be unwittingly selecting against underrepresented groups and U.S. citizens. This effect is easily inferred when combining the race, gender, and citizenship score differences with the use of strict cutoffs (or even preferences) based on GRE scores. Unfortunately, use of minimum acceptable GRE scores in graduate admissions is a common practice throughout the disciplines (23) and in physics specifically (19, 24). Approximately 25% of physics Ph.D. programs publicize to potential applicants a minimum acceptable GRE-P score around 700 (55th percentile). The representation of the U.S. test takers above this level is very different from the applicant pool: Hispanics and Blacks are 6.2 and 1.8% of test takers, respectively, but only 4.1 and 0.6% of those whose scores exceed 700; Asians are 7.8% of test takers, but their above-700 representation is 11.4%; the representation of Whites is unchanged at 78%; women are 20% of test takers, but only 11% of those scoring above 700.

Physics Ph.D. completion study

The goal of this study was to ascertain which of the common quantitative admissions parameters in physics are significantly correlated with Ph.D. completion. To this end, we requested student-level data from all departments that awarded more than 10 Ph.D.’s per year. We requested the following information about students who matriculated in 2000 through 2010: UGPA, GRE-Q, GRE-V, GRE-P, GGPA (graduate GPA), final disposition of student (i.e., Ph.D. earned or not), start and finish years, and demographic information. These data were then analyzed with multivariate logistic regression techniques to identify the extent to which the independent parameters can be used to predict Ph.D. completion probability.

We received data from 27 programs (a response rate of about 42%), representing programs with a broad range of National Research Council (NRC) rankings; the dataset includes peers and aspirational peers for every type of physics Ph.D. program in the United States. We include the doctoral programs’ NRC ranking (25) as a categorical variable. As the NRC only gives confidence intervals for program rank, we created a ranking for this study by averaging the 5 and 95% confidence bounds for the NRC regression-based ranking (NRC-R) and rounded this up to the nearest five to protect the confidentiality of participating programs. This led to a ranking range of 5 to 105. We divided the programs into terciles of approximately equal number of records, categorized as Tier 1 (highest ranked, NRC-R ≤ 20), Tier 2 (25 ≤ NRC-R ≤ 55), and Tier 3 (NRC-R > 55). By analyzing data from Ph.D. programs whose NRC ranking varies widely, we have data from highly selective to much less selective programs, providing us with greater variation in GRE scores than predictive validity analyses deriving from a single program.

Our analytic sample included all students in 24 programs for which start year was available. We identified start year as a sample inclusion criterion because it would be impossible to determine whether Ph.D. noncompletion was simply due to too few years of enrollment without this. These data cover 3962 students, which correspond to roughly 13% of matriculants to all U.S. physics Ph.D. programs during the years studied. In the analytic sample, 18.5% are women of any race or citizenship and 58.4% are U.S. citizens. The racial composition of U.S. citizens in the dataset is 63.6% White, 1.3% Black, 2.4% Hispanic, 0.2% Native American, 4.1% Asian, 0.9% multiple or other races, and 27.6% race unavailable. Excluding the cases for which race was unavailable, the sample is thus roughly representative of annual Ph.D. production in U.S. physics for gender, race, and citizenship, as indicated in Table 1.

We model Ph.D. completion as a function of UGPA (on a four-point scale), GRE scores (GRE-Q, GRE-V, and GRE-P), gender (man or woman), citizenship (U.S. or non-U.S.), race/ethnicity, and NRC ranking. We use multivariate logistic regression to improve upon the correlation coefficient as a measure of validity. Given that multiple parameters may be associated with completion, a multivariate approach allows us to isolate how individual parameters relate to this outcome, controlling for others that may or may not relate. In this case, the logistic regression provides a best-fit probability of Ph.D. completion (P) versus noncompletion (1 − P) as a function of independent model parameters. The “logit,” l, associated with each independent variable is defined as the natural log of the odds ratio. As an example, for a univariate model based on UGPA

$$\mathit{l}(\text{UGPA})= \text{ln}\frac{\mathit{P}(\text{UGPA})}{1-\mathit{P}(\text{UGPA})}$$

The logit is assumed to vary linearly with the parameter, e.g., l(UGPA) = a + bUGPA, where a and b are fit parameters. A model with one independent parameter linking UGPA to completion probability can then be written as P(UGPA) = 1/(1 + exp(− a − bUGPA)). The coefficient associated with UGPA is interpreted as the change in the log of the odds of Ph.D. completion that is associated with a one-point increase in GPA. The interpretation is similar in multivariate analyses, but each coefficient estimate also takes into account (i.e., controls for) simultaneous relationships that other model parameters may have with Ph.D. completion. As such, multivariate models provide a more complete, precise picture than bivariate correlation coefficients of what explains an outcome and of individual parameters’ relationships with the outcome. It is important to note that bivariate correlation coefficients, while easier to compute, include the influence of confounding factors that are also related to the outcome of interest and therefore are inadvisable as a basis for policy decisions. Last, we use a standard P value of 0.050 or less to gauge statistical significance in this article, recognizing the limitations of this metric (26).

RESULTS

Validity analyses conducted on an entire population assume that factors affecting the outcome do not vary categorically or in magnitude for subgroups. We make no such assumptions, based on anecdotal evidence in physics and published research in other disciplines that the GRE’s validity may vary by subgroups (27–29). In addition to estimating the model on the entire sample, we therefore stratified by gender and citizenship and modeled Ph.D. completion separately for these samples. We report results for the samples of U.S. female, U.S. male, U.S. only, and all students. Table 2 reports regression coefficients in terms of both logit and odds ratio with their associated SEs for the four different analytic samples. We summarize the findings of the analysis first by model and then by parameter.

Table 2. Multivariate logistic regression results modeling physics Ph.D. completion in four analytic samples.

The coefficients for logit and odds ratios (ORs) for Ph.D. completion are reported, along with their SEs. Tier 1 (highest ranked, NRC-R ≤ 20), Tier 2 (25 ≤ NRC-R ≤ 55), and Tier 3 (NRC-R > 55). Reference groups are Tier 3 for ranking and White for race/ethnicity. *P < 0.05; **P < 0.01; ***P < 0.001.

	All students		U.S. only		U.S. female		U.S. male
	(N = 3962)		(N = 2315)		(N = 402)		(N = 1913)
	Logit	OR	Logit	OR	Logit	OR	Logit	OR
	(SE)	(SE)	(SE)	(SE)	(SE)	(SE)	(SE)	(SE)
(Intercept)	−1.63** (0.53)	0.2** (0.1)	−2.63*** (0.69)	0.07*** (0.05)	−4.46** (1.65)	1 × 10−2** (0.02)	−2.05** (0.77)	0.1** (0.1)
UGPA	0.31* (0.12)	1.4* (0.2)	0.60*** (0.16)	1.8*** (0.3)	0.9* (0.4)	2.5* (1)	0.47* (0.18)	1.6* (0.3)
GRE-Q	13 × 10−3** (4 × 10−3)	1.013** (0.004)	10 × 10−3* (5 × 10−3)	1.011* (0.005)	0.017 (0.012)	1.02 (0.01)	0.01 (6 × 10−3)	1.010 (0.006)
GRE-V	−1 × 10−3 (2 × 10−3)	0.999 (0.002)	−1 × 10−4 (3 × 10−3)	0.9999 (0.003)	−1 × 10−3 (7 × 10−3)	0.999 (7 × 10−3)	−5 × 10−6 (3 × 10−3)	1.000 (0.003)
GRE-P	3 × 10−3 (2 × 10−3)	1.004 (0.002)	5 × 10−3 (3 × 10−3)	1.005 (0.003)	2 × 10−4 (6 × 10−3)	1.000 (0.006)	5 × 10−3 (3 × 10−3)	1.005 (0.003)
Tier 1	0.69*** (0.1)	2.0*** (0.2)	0.73*** (0.14)	2.1*** (0.3)	0.90** (0.34)	2.5** (0.8)	0.74*** (0.15)	2.1*** (0.3)
Tier 2	0.23* (0.1)	1.3* (0.1)	0.53*** (0.13)	1.7*** (0.2)	0.15 (0.3)	1.2 (0.4)	0.63*** (0.15)	1.9*** (0.3)
Asian	−0.02 (0.28)	1.0 (0.3)	−0.01 (0.28)	0.99 (0.28)	0.09 (0.51)	1.1 (0.6)	−0.07 (0.34)	0.9 (0.3)
Black	−0.77* (0.39)	0.5* (0.2)	−0.72 (0.39)	0.49 (0.19)	−1.08 (1.02)	0.3 (0.3)	−0.65 (0.44)	0.5 (0.2)
Hispanic	−0.60* (0.30)	0.5* (0.2)	−0.56 (0.3)	0.57 (0.17)	0.58 (0.87)	1.8 (1.6)	−0.77* (0.33)	0.5* (0.2)
Native	−15 (240)	0 (0)	−15 (240)	0 (0)	−15 (880)	0 (0)	−15 (270)	0 (0)
Other	−1.2* (0.5)	0.3* (0.1)	−1.14* (0.48)	0.32* (0.15)	−0.62 (0.95)	0.5	−1.29* (0.56)	0.3* (0.2)
Undisclosed	−0.25* (0.1)	0.8* (0.1)	−0.35** (0.13)	0.7** (0.09)	−0.21 (0.29)	0.8 (0.2)	−0.39** (0.14)	0.7** (0.1)
Female	−0.16 (0.1)	0.9 (0.1)	−0.22 (0.13)	0.8 (0.11)
Non-U.S.	0.09 (0.1)	0.9 (0.1)

Findings by model

Starting with U.S. women, the only factors found to correlate with Ph.D. completion are UGPA and graduate program ranking. All else in the model equal, each additional point on the GPA scale is associated with 2.5 times higher odds of Ph.D. completion (P = 0.02); similarly, U.S. women in Tier 1 programs have 2.5 times higher odds of Ph.D. completion than other programs (P = 0.008). Among U.S. women, none of the GREs were found to have significant relationships with Ph.D. completion. We find no differences by race in the probability of degree completion, although the total number of underrepresented women in the sample was small (fewer than 10 for each race).

We have similar findings on the sample of U.S. men: UGPA and graduate program ranking are statistically significant predictors of completion. Each additional point in UGPA is associated with 1.6 times higher odds of Ph.D. completion (P = 0.01); students enrolling in Ph.D. programs ranked 55 or better have two times higher odds of completing than those in lower-ranked programs (P < 0.001). As with U.S. women, no GRE has a significant relationship with Ph.D. completion among U.S. men in the sample. Those who identify as Hispanic (P = 0.02) and Other (P = 0.02) and those for whom race data were unavailable (P = 0.005) have lower odds of degree completion than White students.

The results for an aggregate sample of U.S.-only students resemble those for the U.S. male sample. This similarity is to be expected because men constitute about 80% of the U.S. sample and thus dominate the analysis. All else in the model equal, gender is not a predictor of Ph.D. completion. Unlike separate models of U.S. men and women, however, GRE-Q is positively associated with Ph.D. completion for the combined sample (P = 0.048), perhaps due to the larger sample size.

Estimating the model with all students in this set of Ph.D. programs, including both U.S. and international students, we find results similar to the U.S.-only model. The statistical significance of the UGPA is reduced (P = 0.01) and the effect size is about halved, while that of GRE-Q increases (P = 0.003) but remains of similar magnitude. In this model, being in a Tier 1 program is still associated with two times higher completion odds, whereas the difference between Tier 2 and Tier 3 programs diminishes. All else in the model equal, neither gender nor citizenship status predicts Ph.D. completion. New here is the indication that Black students have lower odds of completion. However, considering that the odds ratio and SE increased marginally, this is likely to be a type I error (false positive).

Findings by parameter

UGPA is the only parameter that remained statistically significant across all models (Table 2). It has the greatest differential for Ph.D. completion, as indicated by its positive slope in Fig. 2. Using the U.S.-only model as an example, women and men with UGPAs of 4.0 have completion probabilities 14 and 12% greater than those with UGPAs of 3.0, respectively.

Fig. 2. Multivariate logistic regression results for the U.S.-only model for UGPA, GRE-Q, GRE-V, and GRE-P for women and men, controlling all other variables (continuous variables held at median values; categorical variables constant; Table 2 reports statistical significance).

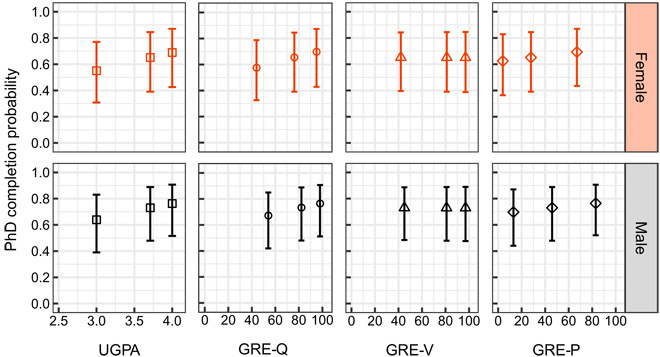
Model results are indicated for the 10th, 50th, and 90th percentile scores for U.S. women and men test takers whose self-reported intended graduate major was physics or astronomy; this range represents the vast majority of scores that can be anticipated by physics and astronomy graduate admissions committees. The whiskers on the model results indicate the 95% confidence intervals associated with Ph.D. completion probability. The relatively flat model results highlight the subtlety of any relationship.

GRE-P scores were not associated with Ph.D. completion at the 0.05 level of statistical significance for any of the models. This is notable because of the large span of scores among graduate students in our sample. As can be seen from Fig. 2, students scoring below the 50th percentile successfully complete the Ph.D. and they do so at a rate similar to those who scored higher. Given the limited statistical significance, the practical significance is also low: For the U.S.-only model, women and men scoring at the 90th percentile for those groups only have completion probabilities 7% greater than those at the 10th percentile.

GRE-Q scores were associated with Ph.D. completion in two models: all students (P = 0.003) and U.S. only (P = 0.048). For the latter, the parameter estimate increases slightly when the U.S. male and female populations are combined and the SE decreases slightly, in accordance with increasing the sample size. These factors, together, yield a GRE-Q parameter for the U.S.-only model where P = 0.048. As such, and as with GRE-P, many of the highest-scoring GRE-Q students do not complete, and many lower-scoring students do complete. The practical significance for the U.S.-only model is limited: Women and men scoring at the 90th percentile for those groups have respective completion probabilities 12 and 9% greater than those at the 10th percentile.

GRE-V scores were not associated with physics Ph.D. completion in any model and were consistently the weakest predictor among the admissions criteria in the model. As an example, the logit coefficient for GRE-V within the all students model was −0.001 ± 0.002 (a negative coefficient means a lower completion probability for higher scores), implying that there is no relationship between probability of Ph.D. completion and GRE-V. This is an important finding because a myth has propagated in the physics community that GRE-V is a good predictor of completion (there is also a myth that women score higher than men on GRE-V; that, too, is false).

Strengths and limitations

This study has two noteworthy strengths linked to two noteworthy limitations. First, we improve on most previous GRE validity studies by including a much larger number and broader range of programs and students. However, our analysis sampled only Ph.D. programs graduating at least 10 students per year, and findings therefore may not generalize to smaller physics programs. Thus, our sample may not generalize to the entire discipline. Our sample does represent programs with NRC rank ranging from 5 to 105, yielding a mix of more and less selective programs. Within them, the sample includes students whose GRE scores represent the tests’ full dynamic range of physics major test takers, minimizing the risk of attenuation bias in our validity estimates. However, it is common for validity studies (30) to focus on Classification of Instructional Programs (CIP) Codes, whereas we focus exclusively on physics, implying that our results may be limited to physics. Note that physics falls under CIP Code 40 (20), along with astronomy and astrophysics, atmospheric sciences and meteorology, chemistry, geological and earth sciences/geosciences, and materials sciences.

Next, although a strength of our methodology is the use of multivariate regression to improve on the usual use of bivariate correlation as a measure of validity (i.e., by controlling for confounding factors), regression results are still correlational and our model contains omitted variable bias. As such, parameters must be interpreted in terms of association with Ph.D. completion, with the understanding that additional factors associated with completion (31) are missing from our model. For example, program rank is positively associated with completion, but we cannot determine here the extent to which this relies on higher-ranked programs selecting students with a greater overall proclivity to complete the Ph.D., or because higher-ranked programs have more resources with which to support students, or because students with more perseverance and drive may tend to apply to higher-ranked schools. Similarly, it is unclear whether the extent to which lower Ph.D. completion odds for students identifying as Black, Hispanic, and Other in some model estimations may be a function of factors that programs can control, such as the quality of advising and mentoring, willingness to accommodate a range of preparation levels, and climate for diversity. Further research is needed to understand the roles of these and other student- and program-level factors to gain a full picture of Ph.D. completion in physics and thus to identify strategies for reducing racial and gender disparities.

DISCUSSION

Among the parameters studied in this sample, we find that Ph.D. program rank and student UGPA are consistently associated with Ph.D. completion, and we find consistent null results for the validity of GRE-V and GRE-P. GRE-Q has a significant relationship with Ph.D. completion among U.S. students as a group and all students (independent of citizenship) but not in samples of U.S. females or U.S. males separately.

The parameter with the strongest, consistent relationship with Ph.D. completion is program rank, with probability of completion significantly higher for more highly ranked programs. As noted above, this study cannot pinpoint how program resources, a more stringent admissions process, and/or the self-selection of applicants to programs may explain this result. Across models, UGPA is the only admissions criterion that consistently predicts Ph.D. completion. In weighing college grades, admissions decision makers should be cognizant that public universities, where the vast majority of underrepresented minority students earn baccalaureate degrees (32), award grades about a third of a letter grade lower than private universities (33, 34). Thus, applying UGPA thresholds would indirectly favor White students, posing a risk to broadening participation aims.

Across models, gender, citizenship, GRE-V, and GRE-P have no bearing on Ph.D. completion. When separately analyzing samples of U.S. females and U.S. males, we see no differences in Ph.D. completion probabilities by GRE-Q, GRE-V, or GRE-P. Only when these samples are combined to increase statistical power does one of these (GRE-Q) reach conventional levels of statistical significance (P = 0.048). The generally weak validity of GRE scores can be explained in a few ways. First, factors related to the testing experience are important. Stereotype threat and test anxiety are real (7, 35), and test taking strategies can be learned by those able to afford coaching (36). With respect to the latter, not all students receive mentoring about the importance of the tests and thus may not undertake serious test preparation. Second, we can interpret weak GRE validity as a function of what it does and does not measure: A single exam taken on a single day represents a small sampling of student skills, not one’s comprehensive capabilities, especially given that these exams are not designed to measure research potential. Third, the standardized exam format is at odds with the culture in U.S. physics; even the subject test fails to capture how we train undergraduates and the problem-solving abilities we expect of graduate students. Undergraduate physics programs in the United States train students to solve complex problems that require hours or days of concerted effort. We know of no undergraduate physics programs in the U.S. that rely on multiple choice exams in courses designed for majors. Last, and specifically with regard to the GRE-P, the topics covered are out of phase with the typical undergraduate physics curriculum in the United States. For example, large fractions of students take quantum mechanics and statistical mechanics in their senior year, either in the same semester as the GRE-P or after it has been offered. Similarly, many smaller institutions, such as minority-serving institutions and liberal arts colleges, often do not have the means to offer a full suite of advanced undergraduate physics coursework. This is important to consider because about 40% of U.S. physics undergraduates come from departments whose highest offered degree is the bachelor’s (37). The potential of students from these institutions to succeed in graduate school may thus not be represented by their GRE-P performance.

Implications

These findings have significant implications for shaping the future of physics in the United States because the GREs are deeply entrenched in the culture of physics. Despite compelling arguments against the use of cutoff scores by the test maker itself, roughly 25% of physics Ph.D. programs have stated minimum scores for admission on the GRE-P and GRE-Q. Perhaps more concerning are recent research findings that suggest that up to 40% of U.S. physics programs use cutoff scores in practice (19). This decontextualized use of GRE scores embodies an admissions process that systematically filters out women of all races and national origins, Hispanics, Blacks, and Native peoples of all genders, and gives preference to international students over U.S. students. The weight of evidence in this paper contradicts conventional wisdom and indicates that lower than average scores on admissions exams do not imply a lower than average probability of earning a physics Ph.D. Continued overreliance on metrics that do not predict Ph.D. completion but have large gaps based on demographics works against both the fairness of admissions practices and the health of physics as a discipline.

This study implies an urgent need for additional research that improves admissions processes in physics and beyond. The community ought to reevaluate admissions criteria and practices to ensure that selection is both equitable and effective for identifying students who can be successful. This effort will require identifying both a broader set of applicant characteristics that predict graduate student outcomes, as well as understanding the characteristics of mentoring and Ph.D. programs that create healthy learning environments. For example, our finding that program ranking was the strongest and most consistent single predictor tells us that the context in which doctoral students are admitted and learn matters for their success.

Further, following the assumption that GRE-P signals preparation in the discipline, the subject test’s limited validity in predicting completion implies that disciplinary preparation itself may be necessary, but insufficient, to identify completers. Discriminating on GRE-P’s implied preparation, rather than a holistic assessment of potential to earn the Ph.D. and conduct research, overlooks applicants who could become strong research physicists. Excellence as a researcher is likely also a function of research mentoring and experience (both before and in graduate school) and socioemotional/noncognitive competencies (e.g., initiative, conscientiousness, accurate self-assessment, and communication), which scholars have linked to performance in other professional and educational domains (38). It is time to think creatively about both assessing these qualities alongside academic preparation as part of a holistic approach to graduate admissions and identifying strategies that connect prospective students to graduate programs in which they will thrive.

MATERIALS AND METHODS

The IPEDS data in Table 1 spanned the years 2009 through 2014; the 5-year average was reported. To count as a physics degree, we added all degree classifications that are primarily given in a physics department. These numbers agree well with those independently gathered by the Statistical Research Center of the American Institute of Physics. The number of first year graduate students was obtained from the National Science Foundation (NSF) and National Institutes of Health (NIH) Survey of Graduate Students and Postdoctorates in Science and Engineering (20). IPEDS does not separate MS from Ph.D. students; we estimated that 90% of the incoming graduate students are intending to pursue the Ph.D. (39).

The validity of various factors in predicting Ph.D. completion may vary by student demographic characteristics, national origin, and program selectivity. For example, considering that the GRE was originally developed on samples of men, we might anticipate that GRE-Q, GRE-V, and/or GRE-P would, individually, have stronger relationships with Ph.D. completion in samples of men than in samples of women. Similarly, cultural differences around frequency of standardized testing may advantage students from countries where these practices permeate the higher education system more than others. Therefore, we stratified the sample by gender, citizenship, and ranking tier and conducted the multivariate regression on each. Although narrowing the analytic sample with this approach reduces statistical power, the sample sizes here are more than sufficient for the used regression methods to detect a reasonably sized effect.

Multiple imputation (multivariate normal algorithm) was necessary to impute missing data for UGPA and GRE-P. This had a minimal effect on the results but increased the sample size by about 20%.

Given that the median time to degree across physics Ph.D. programs is 6 years, some students who started before 2010 were still active at the time of data collection in 2016. The probability of not completing the physics Ph.D. has an exponential time dependence with a time constant of 1.8 years. Thus, students who have been in their programs for three time constants have only a 5% chance of not completing. These students were thus categorized as completers in this study.

ETS changed its general test scale from 200–800 to 130–170 in 2009. Thus, scores were converted to percentiles for each test using concordance tables from ETS to obtain comparable measures across the study.

We conducted a variety of sensitivity tests to ensure the reliability of our findings. We replicated the analyses in both Stata/SE 14.2 and R 3.3.3. Coefficients and P values were equivalent to at least the tenths place in all but a handful of cases, which could be explained by different samples generated by the different multiple imputation packages.

To reduce bias in our estimates that could come from year-to-year variation, we included start year fixed effects. We also examined the stability of coefficients to a variety of model specifications. Given the large share of missing race data, for example, we separately included a dichotomous variable for race unavailable and used only cases for which race data were available. Results via these approaches did not vary substantively, so we used the former to maximize the analytic sample.

Our goal here was not to identify the best predictive model with the minimum number of parameters but rather to understand how all four commonly used admissions metrics (UGPA, GRE-Q, GRE-V, and GRE-P) and the most salient demographic information would contribute to a discussion of metrics and diversity by admissions committees. That said, we did conduct sensitivity tests that examined tested bivariate relationships and added variables to the model stepwise to ensure that we capture both individual relationships and how they operate together to explain Ph.D. completion. However, we report only selected models for the sake of parsimony.

Last, we investigated program-based weights to understand whether variations in the number of records from individual programs would affect our estimates. Weighting schemes had a negligible effect on the results and thus were not used in the analyses reported here.