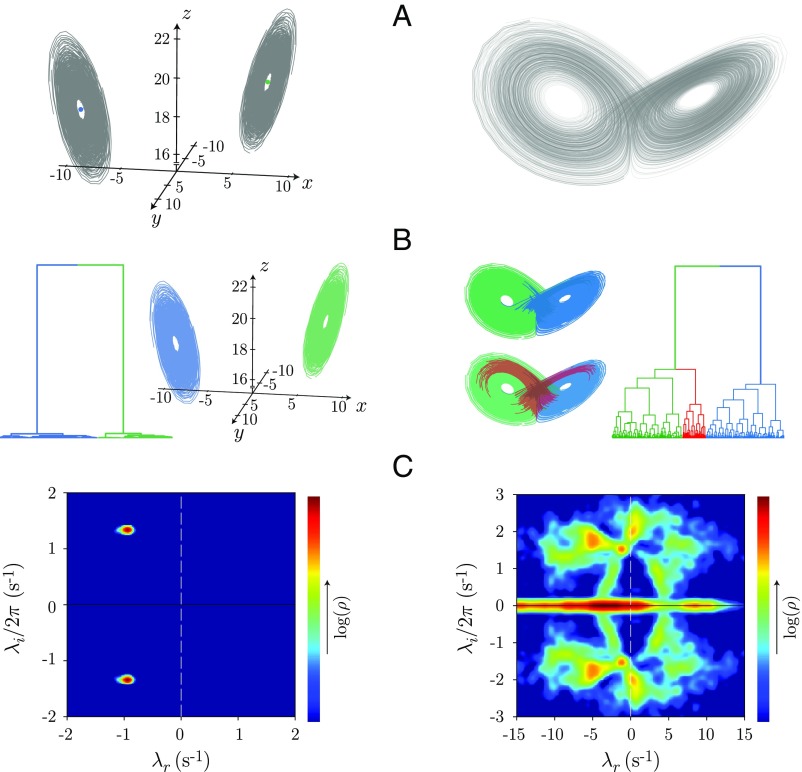
Fig. 2.

Adaptive segmentation of the Lorenz dynamical system and likelihood-based clustering of the resulting model space. (A) Simulated Lorenz system for stable spiral dynamics (Left) $\left\{\rho =20,\beta =8/3,\sigma =10\right\}$ and the standard chaotic regime (Right) $\left\{\rho =28,\beta =8/3,\sigma =10\right\}$. (B) Likelihood-based hierarchical model clustering. In the spiral dynamics, there is a large separation between models from each lobe, while the dynamics within lobe are very similar. In the chaotic regime, the model-space clustering first divides the two lobes of the attractor, and the full space is intricate and heterogeneous. (C) Dynamical eigenvalue spectrum for each regime, ${\lambda }_r$ and ${\lambda }_i$, respectively represent the real and imaginary eigenvalues. The spiral dynamics (C, Left) exhibits a pair of stable, complex conjugate peaks, while in the chaotic regime (C, Right), we find a broad distribution of eigenvalues, often unstable, reflecting the complexity of the chaotic attractor.