Fig. 4.

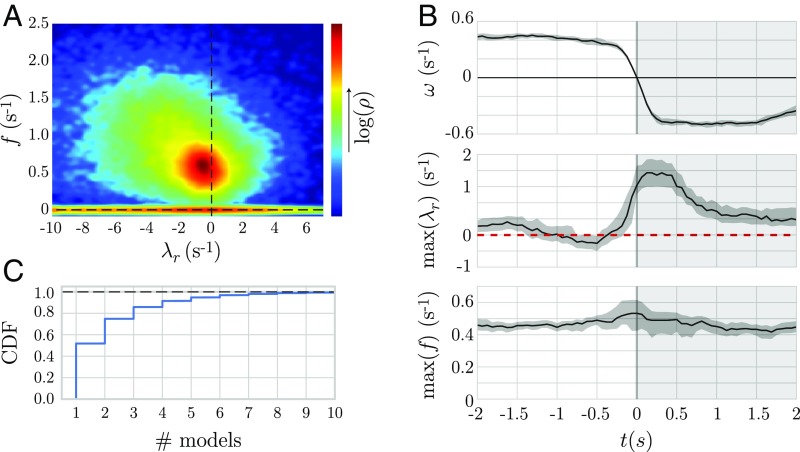
Linear posture dynamics in C. elegans is distributed across an instability boundary with spontaneous reversals evident as a bifurcation. (A) The eigenvalues of the segmented posture time series reveal a broad distribution of frequencies $f=\left|\text{Im}\left(\lambda \right)\right|/2\pi$ with a peak $f\sim 0.6\hspace{0.17em}{\mathrm{s}}^{-1}$ that spills into the unstable regime. (B) We align reversal events and plot the maximum real eigenvalue (${\lambda }_r$) and the corresponding oscillation frequency. As the reversal begins, the dynamics become unstable, indicating a Hopf-like bifurcation in which a pair of complex conjugate eigenvalues crosses the instability boundary. The shaded region corresponds to a bootstrapped 95% confidence interval. (C) Instabilities are both prevalent and short-lived. We show the cumulative distribution function (CDF) of the number of consecutive stable or unstable models, demonstrating that bifurcations also occur on short times between fine-scale behaviors.