Fig. 9.

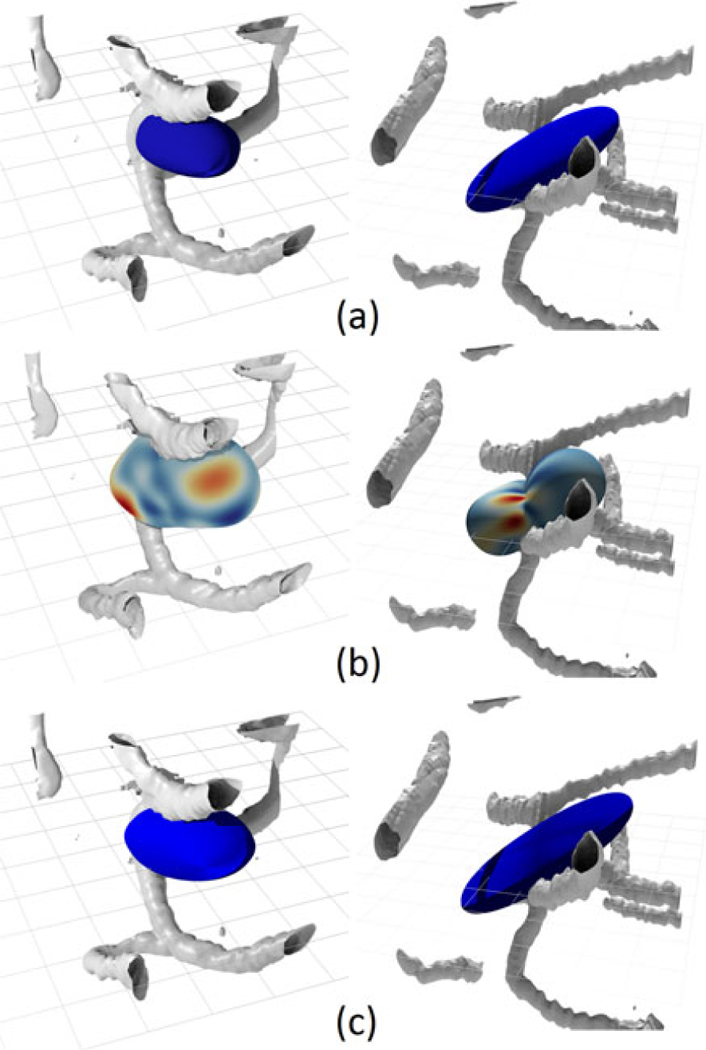
To demonstrate the viability of both the spherical harmonics and the superquadrics we display some cases of both used to represent small networks with only a few fibers (a, b, c). From top to bottom are length-direction superquadric, a spherical harmonic with an average radius color map and flow-volume superquadric superimposed over small number of segmented fibers (grey). We show two types of networks, a more homogeneous case (left) and a more heterogeneous case (right). The harmonic is generate with l = 8 and N = 100k. The network on the left contains fibers with relatively constant radii and the network on the right contains fibers of varying radii. All three cases are presented at optimal viewing angles for demonstrating the shapes of the glyphs relative to the network. The color maps for such small network on the spherical harmonic surfaces tend to be quite sparse due to a smaller number of fibers. In these sparse cases they represent the actual direction of propagation of fibers. The volume and direction superquadrics are much better at representing the bi-directional modality common in these mini-networks. The distinct difference between the volume (c) and the length (a) glyphs is a direct result of the presence of fibers with varying radii. This difference is a lot less prominent in a more homogeneous network.