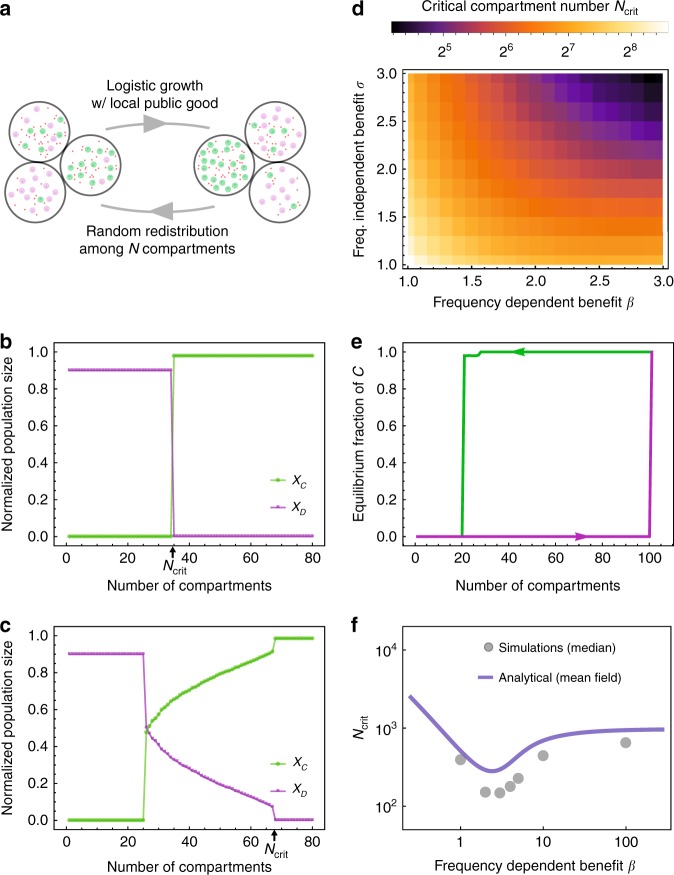
Fig. 5.

Fluctuations in neighborhood size can stabilize cooperation. a Schematic overview of the quasi-spatial model. N compartments are filled with producers and free-riders (a compartment can be empty). The system evolves from time t₀ to t₀ + Δt according to the system governed by the Supplementary Equation (S42). We repeatedly “mixed” (multinomial sampling Y-times into the N compartments) the system followed by selection for a time T_S = 10/α. b For β < σ the system suddenly transitions to the all-C state with increasing number of compartments (decreasing effective neighborhood size). Parameters: α = 1, β = 2, σ = 3, κ = 0.5, δ_C = 0.1, δ_D = 0.1, K = 1000, C(0) = D(0) = 50, T_s = 10. c For β > σ the system transitions to coexistence before equilibrating to the all-C state with increasing number of compartments (decreasing effective neighborhood size). Parameters: α = 1, β = 5, σ = 2, κ = 0.5, δ_C = 0.1, δ_D = 0.1, K = 1000, C(0) = D(0) = 50, T_s = 10. d Calculation of steady state and location of N_crit for small β. The system transitions directly to the producer-only state. Parameters: α = 1, κ = 0.5, δ_C = 0.1, δ_D = 0.1, K = 1000, C(0) = D(0) = 50, T_s = 10. e Hysteresis could be observed when changing N without re-initializing the population (parameters are the same as in b). f Predicted N_crit using mean-field theory compared to the numerically obtained points. Parameters: α = 1, σ = 1, κ = 0.5, δ_C = 0.1, δ_D = 0.1, K = 1000, C(0) = D(0) = 50, T_s = 10