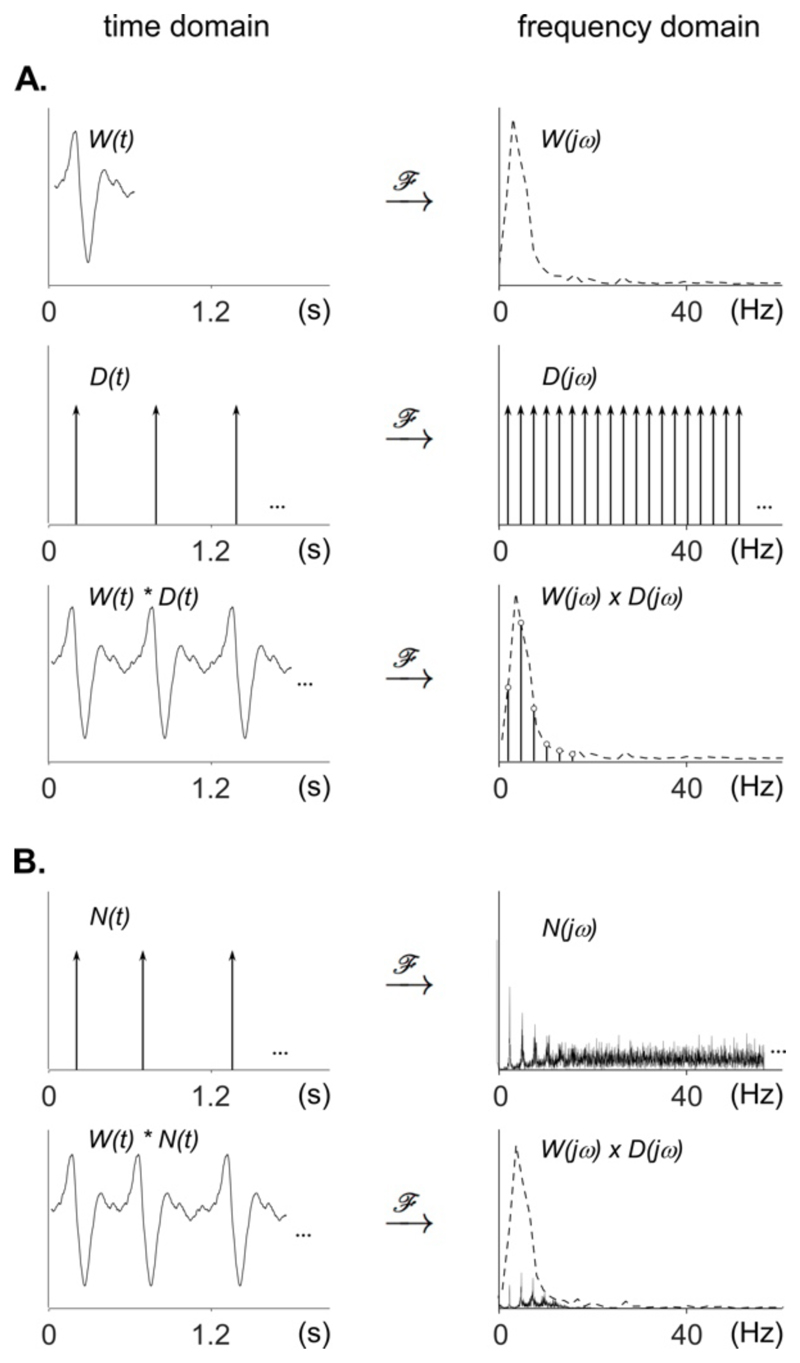
Figure 1. Time and frequency domain representation of periodic and non-strictly-periodic signals.

A. Time domain and frequency domain representations of a unitary waveform W(t), a periodic train of impulses (Dirac comb; D(t)), and a periodic signal corresponding to the convolution of W(t) and D(t) in the time domain, and the multiplication of W(jω) and D(jω) in the frequency domain. Note that the Fourier transform of the periodic signal has a spectrum that concentrates on the fundamental frequency and harmonics determined by the periodicity of the Dirac comb, with a relative amplitude distribution that is determined by the shape of the spectrum of the unitary waveform. B. Time domain and frequency domain representations of a non-strictly-periodic signal corresponding to the convolution of W(t) with a non-strictly-periodic train of impulses N(t). In contrast to the spectrum of the strictly-periodic Dirac comb D(jω), the frequency spectrum of the non-strictly-periodic train of impulses N(jω) is not constituted of isolated peaks at the fundamental frequency and harmonics. Instead, the energy of the signal spreads to surrounding frequencies, and the spectrum will become more and more random if the non-periodicity is increased. The spectrum of the non-strictly-periodic signal obtained by multiplying the spectrum W(jω) of the unitary waveform with the spectrum N(jω) of the non-strictly-periodic train of impulses, contains peaks having a lower amplitude as compared to the strictly-periodic signal.