Figure 4.

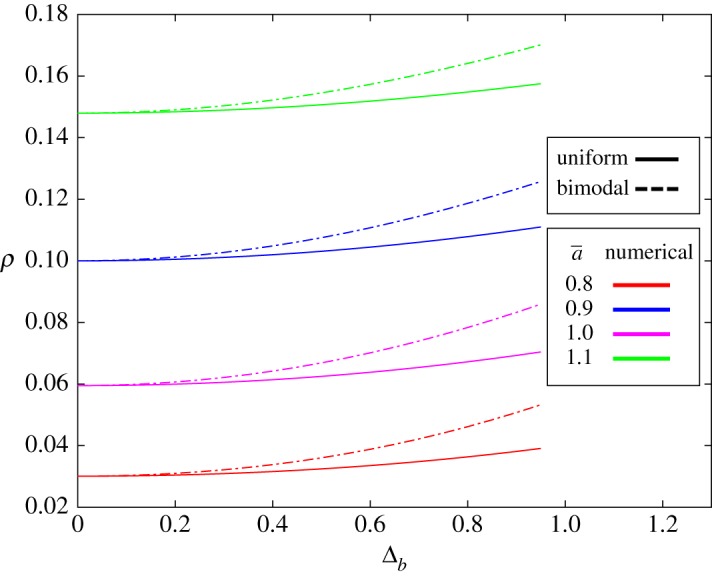
Fixation probability of the mutant type, A, as a function of (half) the width of the resident fitness distribution, Δ_b. The fitness values for the resident are uniformly distributed on $[\overline{b}-{\mathrm{\Delta }}_b,\overline{b}+{\mathrm{\Delta }}_b]$ (solid line), where $\overline{b}=1$. Similarly, for a bimodal distribution, the fitness values for the resident are either $\overline{b}-{\mathrm{\Delta }}_b$ or $\overline{b}+{\mathrm{\Delta }}_b$, each chosen with probability $\frac{1}{2}$ (dashed lines). The population size is N = 10, and $\overline{a}=0.8,0.9,1.0$ and 1.1 (without any mutant fitness heterogeneity). The results are obtained from exact solutions of the Kolmogorov equation for the fixation probability. As Δ_b grows, a near-neutral mutant’s fixation probability increases, consistent with amplification.