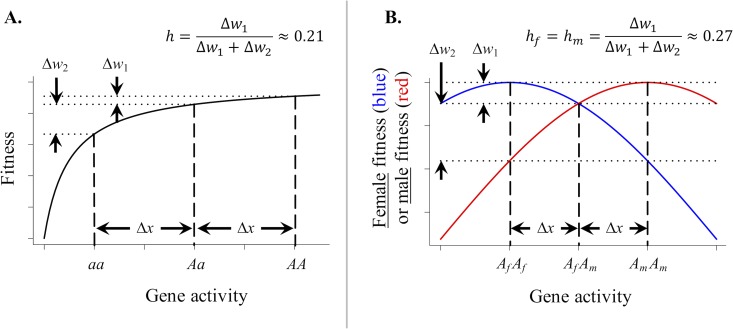
Fig 2. Dominance emerges from concave fitness surfaces.

(A) Wright’s theory of dominance (based on Fig 7 from Wright [41] and Fig 1 from Otto and Bourguet [38]). A concave relation between gene activity and fitness causes deleterious mutations to be partially recessive to beneficial ones. In the example, a beneficial allele, A, and deleterious allele, a, have additive effects on gene activity (i.e., alleles alter gene transcription or function by amount Δx). The diminishing-return relation between fitness and gene activity results in partial recessivity of a with respect to fitness (h < ½). (B) Dominance reversal at an SA gene (based on Fig 1 from Gillespie and Langley [44] and Fig 2 from Fry [27]). The fitness surfaces for females and males (in blue and red, respectively) are each concave but have different optima. The SA alleles have additive effects on gene activity (i.e., by Δx); the concave mapping of fitness on gene activity causes the deleterious variant for each sex to be partially recessive (h_f and h_m < ½), so that A_f is partially recessive in males and A_m is partially recessive in females. A_m, male-beneficial allele; h_f, dominance coefficient of the A_m allele in females; h_m, dominance coefficient of the A_f allele in males; SA, sexually antagonistic.