Figure - PMC

Skip to main content

An official website of the United States government

Here's how you know

Here's how you know

Official websites use .gov
A .gov website belongs to an official government organization in the United States.

Secure .gov websites use HTTPS
A lock ( ) or https:// means you've safely connected to the .gov website. Share sensitive information only on official, secure websites.

View full-text article in PMC

. 2019 Feb 11;9:1744. doi: 10.1038/s41598-018-38372-y

Search in PMC
Search in PubMed
View in NLM Catalog
Add to search

© The Author(s) 2019

Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.

PMC Copyright notice

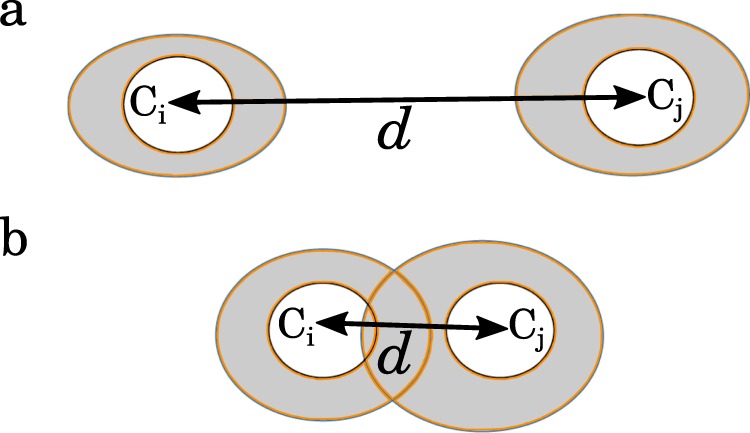
Geometrical illustration of dynamical resistance. Consider a system whose dynamical regimes C_i and C_j are separated in an abstract space by the minimum distance d (C_i, C_j). (a) If d is large, small endogenous and/or exogenous perturbations of the system that lead to small modifications of the system dynamics (grey-shaded areas) do not suffice to induce changes (e.g., a switch from regime C_i to C_j) or a merging of different regimes: the system’s dynamics has a high resistance and can even absorb larger perturbations in the sense that dynamical regimes remain distinguishable. (b) With a small distance between dynamical regimes even tiny perturbations can induce changes or a merging of regimes; the system’s dynamics has a low resistance and can not absorb perturbations in the sense that dynamical regimes remain distinguishable.