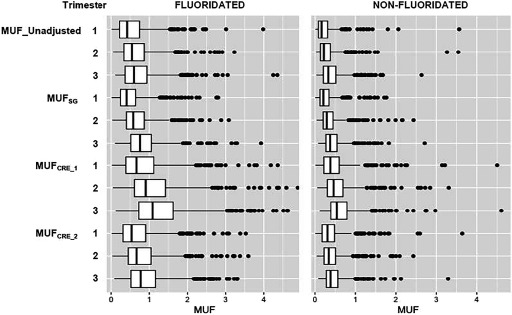
Figure 2.

Pearson r correlations between pairs of trimesters (T1, T2, T3) and intraclass correlation coefficients (ICCs) across trimesters [with 95% confidence interval (CI)] for ${\log }_{10}\text{-transformed}$ maternal urinary fluoride (MUF) levels without adjustment, with adjustment for specific gravity (${\text{MUF}}_{\text{SG}}$), and with adjustment for creatinine using two methods of adjustment (${\text{MUF}}_{\text{CRE}\_1}$ and ${\text{MUF}}_{\text{CRE}\_2}$). Individual data points represent individual observations, solid lines represent regression lines.