A Fast Solver for Large Scale Multistate Bennett Acceptance Ratio Equations

Abstract

The multistate Bennett acceptance ratio method (MBAR) and unbinned weighted histogram analysis method (UWHAM) are widely employed approaches to calculate relative free energies of multiple thermodynamic states that gain statistical precision by employing free energy contributions from configurations sampled at each of the simulated λ states. With the increasing availability of high throughput computing resources, a large number of configurations can be sampled from hundreds or even thousands of states. Combining sampled configurations from all states to calculate relative free energies requires the iterative solution of large scale MBAR/UWHAM equations. In the current work, we describe the development of a fast solver to iteratively solve these large scale MBAR/UWHAM equations utilizing our previous findings that the MBAR/UWHAM equations can be derived as a Rao-Blackwell estimator. The solver is implemented and distributed as a Python module called FastMBAR. Our benchmark results show that FastMBAR is more than 2 times faster than the currently, and widely used solver, pymbar, when it runs on a central processing unit (CPU) and more than 100 times faster than pymbar when it runs on a graphical processing unit (GPU). The significant speedup achieved by FastMBAR running on a GPU is useful not only for solving large scale MBAR/UWHAM equations but also for estimating uncertainty of calculated free energies using bootstrapping where the MBAR/UWHAM equations need to be solved multiple times.

Graphical Abstract

The multistate Bennett acceptance ratio method (MBAR)¹ and unbinned weighted histogram analysis method (UWHAM)² are widely used to calculate relative free energies of multiple states utilizing configurations sampled from each of these states. For instance, they are routinely employed in alchemical free energy calculations,³ umbrella sampling,⁴ and temperature replica exchange simulations⁵ to calculate relative alchemical free energies and potentials of mean force. Although MBAR and UWHAM are derived from different perspectives and viewed as generalizations of the Bennett acceptance ratio method⁶ (BAR) and weighted histogram analysis method⁴ (WHAM), respectively, they are mathematically equivalent and solve the same equations (Eq. 4 below), which we call the MBAR/UWHAM equations.

Due to the advances of hardware and software in parallel computing for molecular dynamics simulation, a large number of configurations can be sampled from hundreds or even thousands of states to study complex biological systems.⁷ Calculating the free energies of these states poses the challenge of solving large scale MBAR/UWHAM equations. To address the challenge, Tan et al.⁸ and Zhang et al.⁷ proposed to use locally weighted histogram analysis and stochastic solution approaches to approximate the solution of global MBAR/UWHAM equations instead of directly solving the global MBAR/UWHAM equations. In this letter, we took a different approach and developed a fast solver for the direct solution of the large scale global MBAR/UWHAM equations. This solver was inspired by our previous discovery that the MBAR/UWHAM equations can be derived as a Rao-Blackwell estimator.⁹ This derivation gives rise to equations (Eq. 5 below) that are equivalent to but more symmetrical than the original MBAR/UWHAM equations (Eq. 4 below) and, most importantly, can be more efficiently solved by optimizing a convex function.

Derivation of the MBAR/UWHAM equations as a Rao-Blackwell estimator.

Given a thermodynamic system whose coordinates are represented using $\overrightarrow{x}$, let us assume that we are interested in calculating the relative free energies of the system in M different thermodynamic states. The potential energy function of the system in the ith state is given as $U_i\left(\overrightarrow{x}\right)$ and the relative free energies of the system in these states are represented as $\left\{G_i^{*},i=1,2,\hspace{0.33em}\dots ,\hspace{0.33em}M\right\}$. To calculate the relative free energies, conformations of the system need to be sampled from each state based on the corresponding Boltzmann distribution. For the ith state, let us assume that N_i conformations are sampled and their coordinates are represented as $\left\{{\overrightarrow{x}}_i^k,k=1,2,\hspace{0.33em}\dots ,\hspace{0.33em}{N}_i\right\}$. To estimate the relative free energies, we can pool conformations sampled from all M states and view all the conformations, $\left\{{\overrightarrow{x}}_i^k,k=1,2,\hspace{0.33em}\dots ,\hspace{0.33em}{N}_i,i=1,2,\hspace{0.33em}\dots M\right\}$, as samples drawn from a generalized ensemble

$$p\left(\text{λ}=i,\overrightarrow{x}\right)\hspace{0.33em}\propto \text{ exp}\left(-\left[U_i\left(\overrightarrow{x}\right)+b_i\right]\right),$$ (1)

where λ is a discrete variable representing the index of states and b_i is a biasing energy added to the ith state so that the relative populations of conformations sampled from M states, $\left\{N_i,i=1,2,\hspace{0.33em}\dots ,\hspace{0.33em}M\right\}$, match the free energies of states in the generalized ensemble. With the biasing energy b_i added to the ith state, the relative free energy of the ith state in the generalized ensemble becomes $G_i=G_i^{*}+b_i$. To match the population of conformations sampled in the ith state, b_i needs to satisfy the condition

$$G_i=G_i^{*}+b_i=-\ln \frac{N_i}{N},$$ (2)

where $N={\sum }_{i=1}^M{N}_i.$ With the sampled conformations, $\left\{{\overrightarrow{x}}_i^k,k=1,2,\hspace{0.33em}\dots ,\hspace{0.33em}{N}_i,i=1,2,\hspace{0.33em}\dots M\right\}$, from the generalized ensemble (1), the free energy of the ith state can also be estimated using a Rao-Blackwell estimator and normalized conditional probabilites from Eq. (1), i.e.,

$$\begin{gathered} G_i=-\ln P\left(\lambda = i\right) \\ \hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}=-\ln \frac{1}{N}\sum _{j=1}^M\sum _{k=1}^{N_i}p\left(\lambda = i|{\overrightarrow{x}}_i^k\right) \\ \hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}=-\ln \frac{1}{N}\sum _{j=1}^M\sum _{k=1}^{N_j}\frac{\exp \left[-\left(U_i\left({\overrightarrow{x}}_j^k\right)+b_i\right)\right]}{{\sum }_{l=1}^M\exp \left[-\left(U_l\left({\overrightarrow{x}}_j^k\right)+b_l\right)\right]}. \end{gathered}$$ (3)

Combining Eq. (2) and Eq. (3) and eliminating the biasing energies b_i yield the MBAR/UWHAM equations^1,2

$$G_i^{*}=-\ln \sum _{j=1}^M\sum _{k=1}^{N_j}\frac{\exp \left[-U_i\left({\overrightarrow{x}}_j^k\right)\right]}{{\sum }_{l=1}^M{N}_l\cdot \exp \left[-\left(U_l\left({\overrightarrow{x}}_j^k\right)-G_l^{*}\right)\right]}.$$ (4)

The relative free energies of the system in the M states, $\left\{G_i^{*},i=1,2\hspace{0.33em}\dots ,\hspace{0.33em}M\right\}$, can be calculated by solving the self-consistent equations (4). Alternatively, keeping the biasing energies b_i as unknown variables and eliminating the free energies $G_i^{*}$ when combining Eq. (2) and Eq. (3) yield more symmetrical equations:

$$\sum _{j=1}^M\sum _{k=1}^{N_j}\frac{\exp \left[-\left(U_i\left({\overrightarrow{x}}_j^k\right)+b_i\right)\right]}{{\sum }_{l=1}^M\exp \left[-\left(U_l\left({\overrightarrow{x}}_j^k\right)+b_l\right)\right]}=N_i.$$ (5)

In this way, the relative free energies, $G_i^{*}$, can be calculated using Eq. (2) after solving Eq. (5) for b_i. Compared with Eq. (4), Eq. (5) is more symmetrical in the sense that the denominator and numerator of the summed term have similar exponential terms and the extra multiplication of N_l in Eq. (4) is eliminated. This makes the calculation of the summed ratio term in Eq. (5) numerically more stable and reduces the number of floating point operations. More importantly, Eq. (5) can be solved by minimizing a convex function as shown below.

Solving MBAR/UWHAM equations by optimizing a convex function.

If we define

$$g_i\left(b_1,b_2,\hspace{0.33em}\dots ,\hspace{0.33em}{b}_M\right)=-\frac{1}{N}\sum _{j=1}^M\sum _{k=1}^{N_j}\frac{\exp \left[-\left(U_i\left({\overrightarrow{x}}_j^k\right)+b_i\right)\right]}{{\sum }_{l=1}^M\exp \left[-\left(U_l\left({\overrightarrow{x}}_j^k\right)+b_j\right)\right]}+\frac{N_i}{N},$$ (6)

then solving Eq. (5) is equivalent to identifying the zero point of the functions: $g_i\left(b_1,b_2,\hspace{0.33em}\dots ,\hspace{0.33em}{b}_M\right),\hspace{0.33em}i=1,2,\hspace{0.33em}\dots ,\hspace{0.33em}M$. It is easy to verify that the function g_i(b_1, b₂, …, b_M ) is the derivative function of the following function f(b_1, b₂, …, b_M ) with respect to b_i:

$$f\left(b_1,b_2,\hspace{0.33em}\dots ,\hspace{0.33em}{b}_M\right)=\frac{1}{N}\sum _{j=1}^M\sum _{k=1}^{N_j}\ln \left(\sum _{l=1}^M\exp \left[-\left(U_l\left({\overrightarrow{x}}_j^k\right)+b_l\right)\right]\right)+\sum _{i=1}^M\frac{N_i}{N}{b}_i,$$ (7)

i.e., $g_i\left(b_1,b_2,\hspace{0.33em}\dots ,\hspace{0.33em}{b}_M\right)=\partial f/\partial b_i.$ Because the function f(b_1, b₂, …, b_M ) is a convex function,¹⁰ identifying the zero point of its derivative is equivalent to minimizing the function f(b_1, b₂, …, b_M ). Compared with solving the nonlinear Eq. (5) directly, minimizing the convex function (7) has the advantage of a broader choice of robust algorithms. In order to make the solver applicable to solving large scale MBAR/UWHAM equations, in which the value of M can be in the hundreds or even thousands, the quasi-Newton optimization method called L-BFGS¹¹ was utilized to minimize the convex function (7) to avoid the calculation of its Hessian matrix. We note that solving the MBAR/UWHAM equations by minimizing a convex function was first explicitly described in reference [2], but the convex objective function proposed here is different from that in reference [2] and is also derived from a different perspective. We also note that in the current implementation of pymbar (version 3.0.4 from https://github.com/choderalab/pymbar), in addition to the self-consistent iteration and the Newton-Raphson methods originally proposed in reference [1], the MBAR/UWHAM equations can also be solved by minimizing a different objective function using Hessian free optimization methods including the L-BFGS method used in this study.

Results.

Utilizing the method described above, we developed a Python module called FastMBAR for solving larger scale MBAR/UWHAM equations. Compared with the existing Python module pymbar,¹ FastMBAR is more efficient at solving the MBAR/UWHAM equations, especially for large values of M × N, because FastMBAR is accelerated by the use of graphical processing units (GPUs)¹².

To benchmark the relative performance of FastMBAR to pymbar, we applied both pymbar and FastMBAR to solve MBAR/UWHAM equations of varying size. Because the main input of the MBAR/UWHAM equations is a matrix of energies, the size of the MBAR/UWHAM equation system is measured by the number of elements in the input matrix of energies, which is M × N when there are M states and N conformations sampled from those states in total. An energy matrix with a size of M × N was generated by sampling from M one-dimensional harmonic oscillators. For each harmonic oscillator, its equilibrium position was randomly sampled from the normal distribution $\mathcal{N}\left(0,\hspace{0.33em}{10}^2\right)$ and its force constant was randomly sampled from a uniform distribution in the interval of [0.04, 1]. N/M conformations are sampled from each harmonic oscillator. Energy matrices of various sizes were obtained by varying the values of both M and N.

Because the focus of this paper is solving large scale MBAR/UWHAM equations, optimization methods that require calculating the Hessian matrix are not considered. To make a fair comparison between pymbar and FastMBAR, both methods use the same L-BFGS¹¹ optimization method with the same convergence criterion which is that the relative reduction of objective functions is less than 1 × 10⁻¹². Double floating point operations are used in both methods. The computational wall clock times to solve the MBAR/UWHAM equations of various sizes were measured for both pymbar and FastMBAR (Fig. 1A). Compared with pymbar running on a CPU, FastMBAR is more than 2 times faster running on the same CPU and more than 100 times faster running on a current generation gaming GPU. To investigate why FastMBAR is faster than pymbar, we also calculated the number of iterations required by pymbar and FastMBAR to converge and the wall times required to evaluate the objective and gradient functions once. On average, pymbar requires 1.7 times more iterations than FastMBAR running on CPUs or GPUs to converge to the same estimator precision (Fig. 1B, 1D, and Fig. S1-S7). In terms of the wall time required to evaluate the objective and gradient functions, FastMBAR is about 1.5 time faster than pymbar on CPUs and 90 times faster on GPUs (Fig. 1C). Overall, this enables FastMBAR to be about 2.5 times faster than pymbar when it runs on CPUs and about 150 times faster on GPUs.

Figure 1:

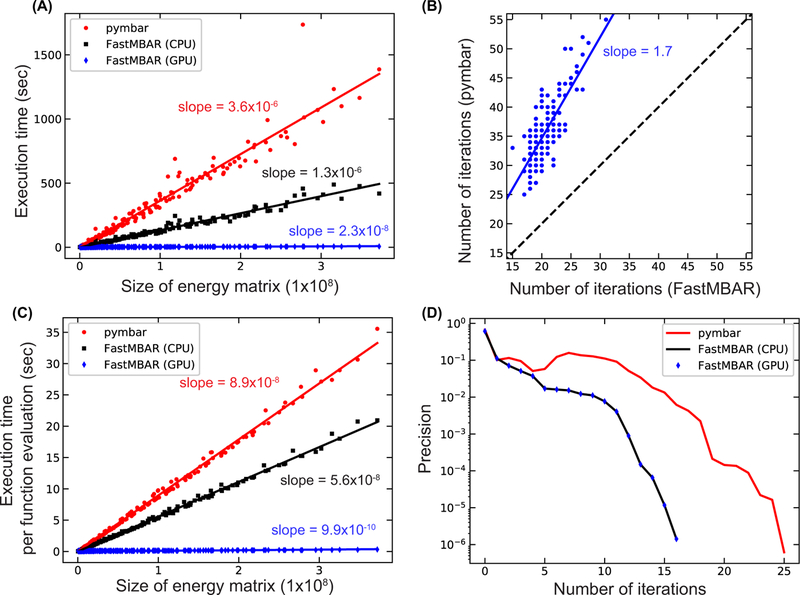
(A) Comparison of wall times required to solve MBAR/UWHAM equations of different sizes by pymbar and FastMBAR. Both pymbar and FastMBAR (CPU) were run on one Intel^® Xeon^® Processor E5520. The GPU used was a NVIDIA^® GEFORCE^® GTX 1080. (B) Number of iterations required by pymbar and FastMBAR (running on CPUs and GPUs) to solve MBAR/UWHAM equations to the same estimator precision (the relative reduction of objective functions is smaller than 1e-12). (C) Wall times required by pymbar, FastMBAR (CPU), and FastMBAR (GPU) to evaluate objective and gradient functions once. (D) Estimator precision changes with the number of iterations for pymbar, FastMBAR (CPU), and FastMBAR (GPU) when solving the MBAR/UWHAM equation with the energy matrix size of 100×12421. Similar plots for solving MBAR/UWHAM equations of other energy matrix sizes can be found in Fig. S1-S7.

The significant speedup provided by FastMBAR running on GPUs is useful not only for solving large scale MBAR/UWHAM equations but also for to perform bootstrapping to estimate the uncertainty of calculated free energies, because the MBAR/UWHAM equations need to be solved multiple times.¹³ Specifically in FastMBAR, the uncertainty of relative free energies is determined by block bootstrapping,¹⁴ which is more reliable than the closed-form asymptotic uncertainty estimate when the observations are correlated and the number of effective samples is small.

In summary, in this letter we have exploited the symmetrical form that the MBAR/UWHAM equations take when expressed as a form of a Rao-Blackwell estimator to develop a fast solution to these coupled iterative equations. When cast as a computational algorithm, our Python-based code performs more than 2 times and two orders of magnitude faster than the widely used pymbar package¹ to solve the same large scale problem on CPUs and GPUs, respectively. This gain in speed facilitates the integration of much larger data sets into free energy analyses as well as the capabilities to utilize statistical methods of uncertainty estimation through bootstrapping. In addition, our implementation for uncertainty estimation through bootstrapping could be further accelerated by utilizing the warm-start technique, where solutions of the previous subproblem are used as the starting point for solving the next subproblem. Our developed code base in Python, FastMBAR, is freely available for download and use at https://github.com/xqding/FastMBAR.