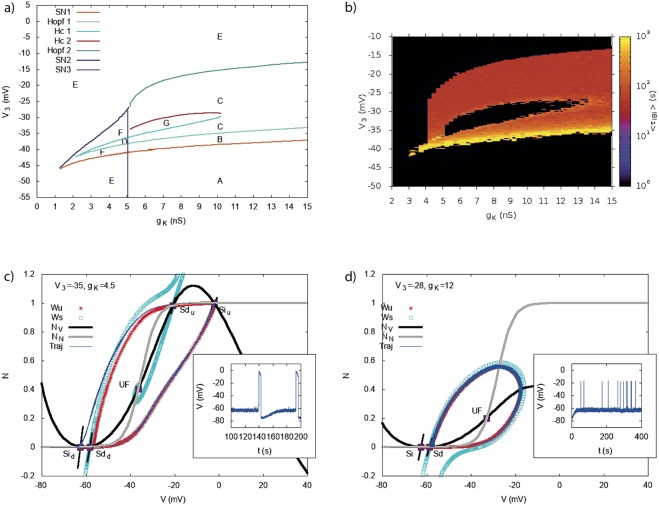
Figure 11.

Bifurcation diagram and heat map of τ_IBI in the plane V₃ − g_K. (a) In region A, there is a stable fixed point with low voltage. In B, 2 stable fixed points coexist with a saddle-point. In C a stable fixed point with low voltage coincides with a stable periodic orbit giving rise to fast oscillations. In region D there are 4 fixed points (2 stable, 2 unstable) and a limit cycle. In region E there is a stable fixed point with low voltage and a stable fixed point whose position depends on g_K and V₃. In region F there are five fixed points, 2 stables. Region G contains 2 stable fixed point (a sink and a focus) separated by an unstable fixed point. Bursting takes place in regions C and D. (b) Heat map of the interburst interval τ_IBI. Same representation as Fig. 5. We sampled the plane g_K, V₃ with a step of 0.25 nS on the g_K axis and 1 mV on the V₃ axis, explaining the irregular shape of the border. (c,d) There is a discrepancy between the heat map and the bifurcation diagram: (i) The bifurcation map does not predict bursting for $g_K\in [4,5]$ nS, $V_3\in \sim [-40,-25]$ mV whereas the heat map shows calcium peaks lasting more than 1 s in this region. This is due to the particular structure of the phase portrait of the Morris-Lecar model in this region and the effect of noise, as shown in (c). This phase portrait has two saddles (Sd) down (Sd_d) and up (Sd_u), and two sinks (Si), down (Si_d) and up (Si_u). The unstable manifold (W_u, in red) of Sd_d connects to Si_u, on the right, and to Si_d, on the left; The unstable manifold of Sd_u connects to Si_u, on the right, and to Si_d, on the left. Thanks to noise, dynamics can leave Si_d and reach Si_u where it stays until sAHP rising drive it back to Si_u. This is illustrated by the blue trajectory (complete system with noise) which follows the unstable manifolds of the Morris Lecar model. The inset shows the trajectory of the voltage for the complete system in the presence of noise. (ii) (d) While the bifurcation diagram predicts bursting for V₃ ~ −28 mV, g_K ~ 12 nS, the heat map does not show bursting in this region (black). This is again due to noise. When the cell is on low rest state (Si) noise drives it to the limit cycle, but after a few oscillations, noise drive the cell back to the rest state Sd (see inset for the voltage trajectory). This effect depends on the distance between the two fixed points Si, Sd, fixed by the model parameters, and on the noise intensity σ (here 4 pA ${\mathrm{ms}}^{\frac{1}{2}}$).