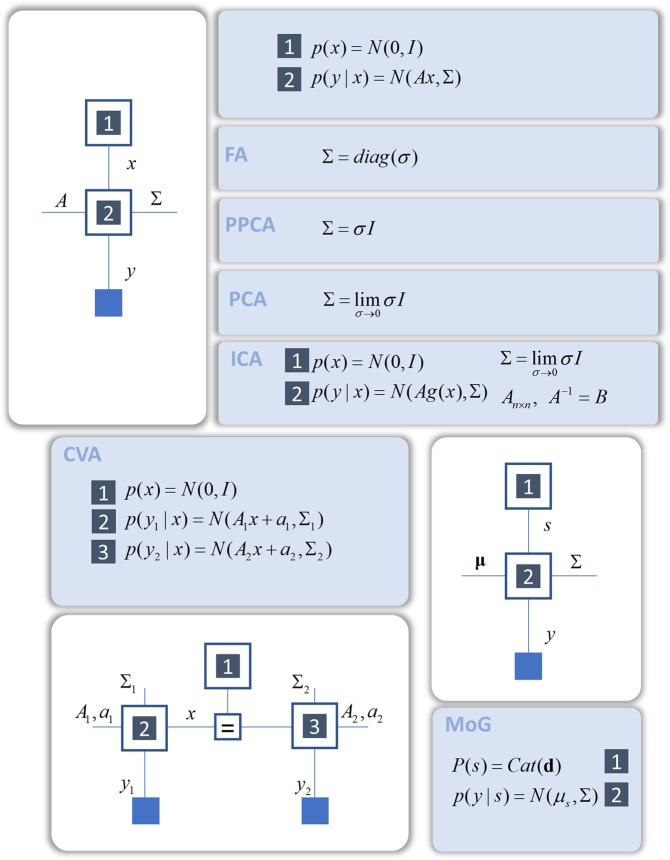
Figure 2.

Commonly used (static) generative models as factor graphs. This figure illustrates the generative models that underwrite many common inferential procedures. In each factor graph, small blue squares indicate observable data, while squares with an equality sign relate their adjoining edges via a delta function factor (shown explicitly in lower right inset in Fig. 3 - Hidden Markov model). Numbered squares relate factors to those in the probabilistic models in the blue panels. This Figure illustrates static models of the sort that underlie factor analysis (FA), probabilistic principle component analysis (PPCA), and principal component analysis (PCA)²¹. Each of these dimensionality reduction techniques relies upon the same generative model, but with different assumptions about the covariance structure of latent causes or sources. Adding in non-linear functions allows this generative model to be extended to incorporate independent component analysis (ICA)⁹⁴, while using two different linear transforms leads to probabilistic canonical variates analysis (CVA)⁹⁵. Incorporating discrete random variables gives mixture models including mixtures of Gaussians (MoG), which form the basis of many clustering algorithms⁹⁶. The notation N indicates a normal (Gaussian) distribution, while Cat means a categorical distribution.