Nucleosynthetic Isotope Variations of Siderophile and Chalcophile Elements in the Solar System

INTRODUCTION

Numerous investigations have been devoted to understanding how the materials that contributed to the Solar System formed, were incorporated into the precursor molecular cloud and the protoplanetary disk, and ultimately evolved into the building blocks of planetesimals and planets. Chemical and isotopic analyses of extraterrestrial materials have played a central role in decoding the signatures of individual processes that led to their formation. Among the elements studied, the siderophile and chalcophile elements are crucial for considering a range of formational and evolutionary processes. Consequently, over the past 60 years, considerable effort has been focused on the development of abundance and isotopic analyses of these elements in terrestrial and extraterrestrial materials (e.g., Shirey and Walker 1995; Birck et al. 1997; Reisberg and Meisel 2002; Meisel and Horan 2016, this volume).

In this review, we consider nucleosynthetic isotopic variability of siderophile and chalcophile elements in meteorites. Chapter 4 provides a review for siderophile and chalcophile elements in planetary materials in general (Day et al. 2016, this volume). In many cases, such variability is denoted as an “isotopic anomaly”; however, the term can be ambiguous because several preand post- Solar System formation processes can lead to variability of isotopic compositions as recorded in meteorites. Here we strictly define the term “isotopic anomaly” as referring to an isotopic deviation from the terrestrial composition resulting from the incorporation of varying proportions of elements with diverse nucleosynthetic origins into a meteorite component or parent body. The term will not be used here to refer to isotopic variations that result from mass-dependent isotopic fractionation, radioactive decay in the Solar System, or spallation effects.

Based on astronomical observations and physical modelling, the formation of the Solar System has generally been thought to have initiated by the collapse of a dense molecular cloud core composed of gas and dust grains, which originated from diverse stellar environments (e.g., Boss 2003). This scenario regarding the birth of the Solar System has largely been corroborated by the discovery of presolar grains in primitive meteorites; presolar grains are remnant circumstellar dust grains which survived various destructive dynamic processes in the early Solar System, such as heating and collision, and were eventually incorporated into the parent bodies of primitive meteorites. Presolar grains are identified by their having isotopic compositions that can be drastically different from terrestrial, and from one another, depending on their mineral types and mode of origin (Zinner 2014). It was initially believed that presolar grains had been thoroughly mixed within the molecular cloud and/or in a turbulent protoplanetary disk, thereby resulting in homogeneous stable isotope compositions for all elements within the solar nebula, excluding some light elements such as hydrogen, carbon, nitrogen, and oxygen (e.g., Kerridge 1985; Clayton and Mayeda 1999). Consistent with this, most early studies of the isotopic compositions of numerous elements failed to find resolved isotopic anomalies on the scale of bulk aliquots of chondrites and differentiated meteorites (e.g., Murthy 1963; McCulloch and Wasserburg 1978a).

The advent of multi-collector inductively coupled plasma mass spectrometers (MC-ICPMS), as well as improvements to thermal ionization mass spectrometers (TIMS) in the 1990s has enabled very high precision measurement of isotope ratios for a variety of elements. These mass spectrometers can efficiently generate ion beams of the elements of interest, which are accelerated and focused by high voltage potentials, then separated by an electromagnet into individual beam courses based on the mass/charge ratio of ions (m/z). Ionization is achieved either by the heat of a metal filament (TIMS), or plasma (ICP-MS). Both types of instruments require the chemical separation and purification of the element of interest, prior to isotopic measurement. This is necessary in order to avoid spectroscopic interferences from isobars and molecular ions. In ICPMS analysis, the purified element is dissolved in diluted acid and aspirated into the plasma ion source. The advantage of MC-ICP-MS is that ionization efficiency is high compared to thermal ionization for most of the elements in the periodic table. This enables isotopic analyses of elements with high ionization potentials (e.g., Zr, Hf), that are difficult or impossible to measure with TIMS. Also, although the plasma ionization source tends to strongly fractionate the isotopes of an element, the fractionation effects are generally stable and can be corrected for by interspersal of standards of known isotopic composition with samples, or by monitoring the isotopic ratio of an element of similar mass and known isotopic composition that is added to the sample. This means that MC-ICP-MS can be used to precisely measure the isotopic compositions of elements that consist of only two isotopes. By contrast, in TIMS analysis, the purified element is loaded on a metallic ribbon (e.g., Re, W, Ta, Pt, Ir), which is heated to cause ionization of the atoms. The advantage of TIMS is that the energy distribution of the ion beam is so small that the fluctuation of the ion beam intensity and the background noise are minimized compared to MC-ICP-MS. Correction for fractionation requires that at least three isotopes be measured. One ratio is used for fractionation correction. Modern MC-ICP-MS and TIMS instruments are now capable of making sub-5 ppm measurements (2 SD) for some isotopic ratios of some elements. This capability has enabled the detection of small but significant isotopic variability among bulk meteorites for some elements (typically at a level of ± 200 ppm or less).

One of the first elements for which isotopic anomalies were identified in bulk planetary materials is Cr. Chromium is characterized by excesses and deficits of the neutron-rich isotope ⁵⁴Cr, compared to terrestrial standards: ε⁵⁴Cr values (parts per 10⁴ deviation of ⁵⁴Cr/⁵²Cr from the terrestrial ratio) in meteorites ranges from −0.7 ε for differentiated meteorites (eucrite, diogenite, mesosiderite, pallasite, angrite, and SNC) to +1.6 ε for CI chondrites (Shukolyukov and Lugmair 2006; Trinquier et al. 2007; Qin et al. 2010). With respect to siderophile and chalcophile elements, planetary scale isotopic variability has been most thoroughly documented for Mo and Ru (Dauphas et al. 2002a; Chen et al. 2010; Burkhardt et al. 2011). By contrast, no isotopic anomalies have yet been documented in bulk meteorites for Os, Te, and Cd, despite extensive searches (Fehr et al. 2005; Yokoyama et al. 2007, 2010; Wombacher et al. 2008). This contrast in the magnitude of isotopic anomalies among different elements may imply that Solar System precursors were not thoroughly homogenized by the dynamic processes operating within the solar nebula, and suggests instead that individual elements acted differently during the nebular processes. The cause of the inconsistency regarding isotope variability has not yet been resolved.

In this chapter we review how nuclear reactions in a variety of stellar environments in the Galaxy produced the elements in the periodic table. We then discuss the nature of presolar grains, the carriers of isotopically anomalous components in the solar nebula at the time of planetesimal formation. Readers seeking more detailed overviews of stellar nucleosynthesis and presolar grains are referred to several recent reviews (Meyer and Zinner 2006; Nguyen and Messenger 2011; Heger et al. 2014; Zinner 2014). In subsequent sections, we review isotopic variability evidenced among siderophile and chalcophile elements, not only in bulk meteorites, but also in chondrite components such as acid leachates and residues, and calcium and aluminum-rich inclusions (CAIs). Finally, we discuss the origin of planetary scale isotopic variability in the solar nebula, specifically focusing on processes that may have led to the decoupling of isotopic anomalies among different elements. Such information is key for understanding the behavior of materials derived from diverse stellar sources in the solar nebula, and decoding how individual planets or planetesimals obtained diverse nucleosynthetic components in varying proportions.

ORIGIN OF ELEMENTS: STELLAR NUCLEOSYNTHESIS

The Big Bang and subsequent nuclear reactions in various stellar environments have produced all of the elements in the universe. Hydrogen (¹H, ²H) is the dominant product of Big Bang nucleosynthesis, while helium (³He, ⁴He) and trace amounts of ⁷Li and ⁷Be were also produced (Fields and Olive 2006). The theory of subsequent stellar nucleosynthesis was established by seminal studies, such as Burbidge et al. (1957) (referred to as the B²FH paper) and Cameron (1957). These studies recognized that elements not produced by the Big Bang were synthesized in tandem with the evolution of stars from birth to death. The pathway of nucleosynthesis is determined by the stellar mass, which can be divided into two general groups; low to intermediate mass stars (< 8 M_☉; M_☉ refers to the mass of the Sun), and massive stars (> 8 M_☉). In the following, we first summarize how stars at the hydrostatic equilibrium stage synthesized elements from He to Fe. We then focus on the nucleosynthesis of elements heavier than Fe, by which most of the siderophile and chalcophile elements are produced.

Production of elements from He to Fe via hydrogen to silicon burning

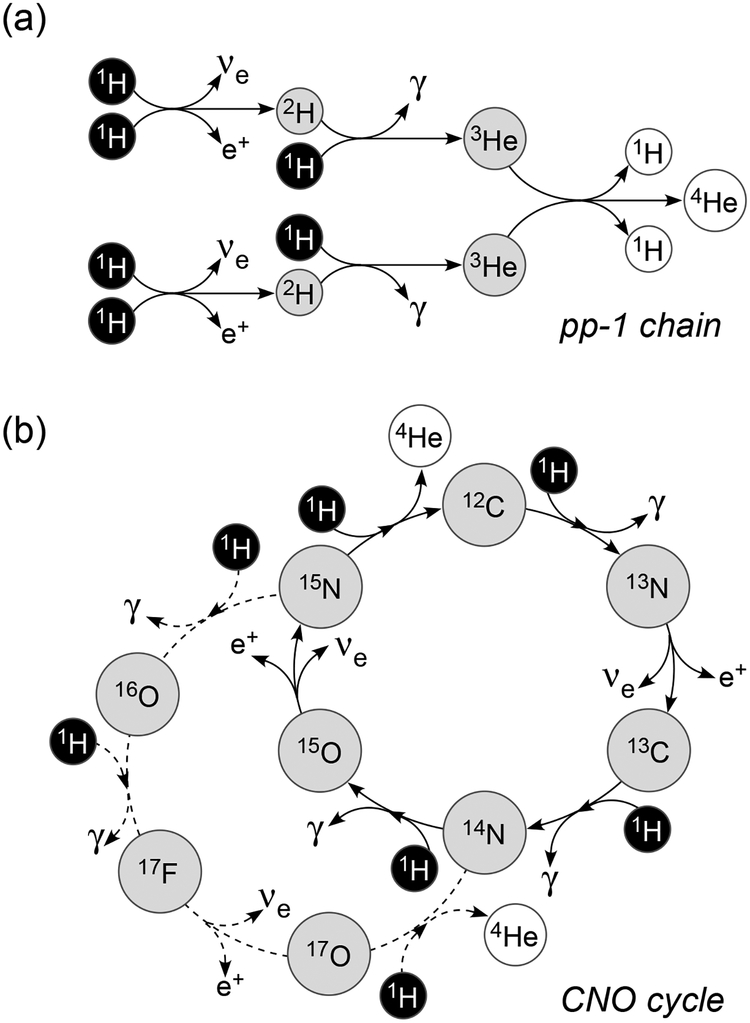
Hydrogen Burning.

The first step of stellar nucleosynthesis begins with H burning, which occurs in main sequence stars. Hydrogen burning is a process in which four ¹H nuclei are converted to ⁴He via three proton-proton reaction chains (pp chains). In stars like the Sun, the burning is via the pp chains, which all commence with the reaction

$${}^1\text{H}+{}^1\text{H}\to {}^2\text{H}+{\text{e}}^{+}+{\mathrm{\nu }}_{\text{e}}$$

In this reaction, one of the two protons converts to a neutron, a very unlikely event in the scattering of two protons, which makes the reaction slow and allows the Sun to have a long lifetime (~10¹⁰ years). The next reaction is

$${}^2\text{H}+{}^1\text{H}\to {}^3\text{He}+\mathrm{\gamma }$$

The pp-1 chain (Fig. 1a), which dominates H burning in the Sun, is completed by

$${}^3\text{He}+{}^3\text{He}\to {}^4\text{He}+2^1\text{H}$$

Figure 1.

Schematic view of hydrogen burning. (a) pp-1 chain and (b) CNO cycle.

At higher temperatures, the pp-2 and pp-3 chains can dominate in which ⁴He is synthesized via ⁷Be and ⁷Li (pp-2) and ⁷Be, ⁸B, and ⁸Be (pp-3). The pp-1 chain is currently dominant (85%) in the interior of the Sun, and the pp-2 (15%) and pp-3 (0.02%) chains are much less active because they require temperatures higher than that of the center of the Sun. Besides the pp chain, the CNO cycle is another type of H burning which occurs in stars heavier than the Sun with core temperatures higher than 2 × 10⁷ K. This is a dual cycle consisting of the CN-and NO-cycles, in which four ¹H nuclei are consumed to produce ⁴He, with reactions catalyzed by C, N, and O atoms co-existing in the star (Fig. 1b). The catalytic C, N, and O must be inherited from pre-existing stars.

Helium Burning.

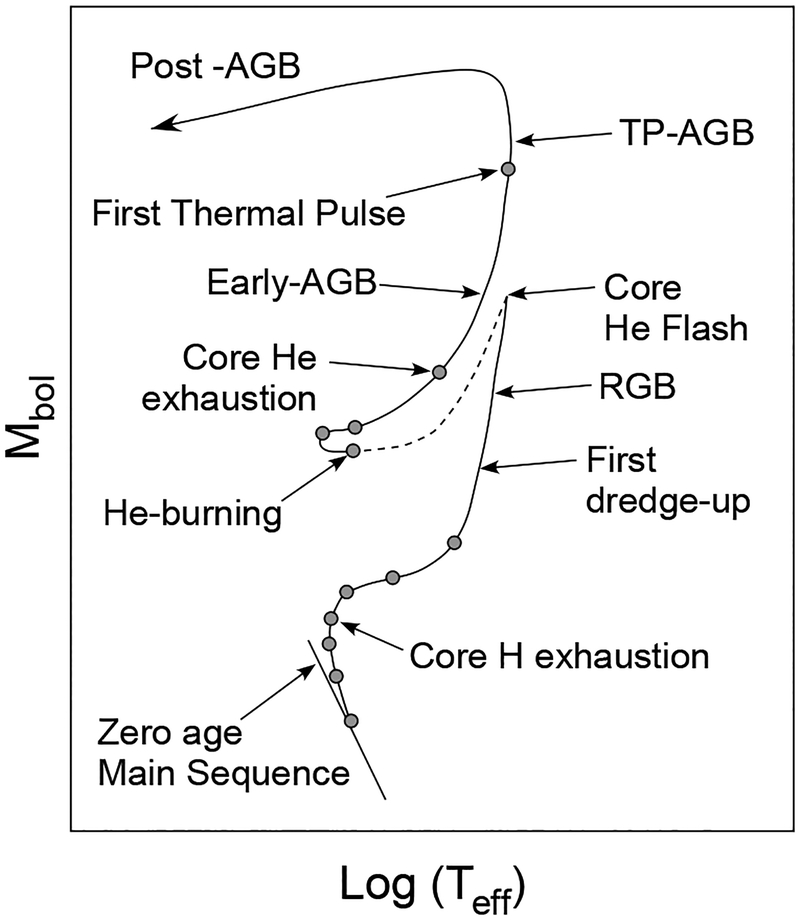
As H burning proceeds, ¹H atoms in a stellar center are exhausted and converted into ⁴He, forming a He core surrounded by a H-rich shell. No nuclear fusion initially occurs in the He core while the core begins to gravitationally contract, resulting in increasing pressures and temperatures. This contraction leads to H burning at the bottom of the H-rich shell, increasing the star’s luminosity. At this point the H-rich shell starts to expand significantly, and surface temperatures decrease. During this phase, termed the red giant phase, the star begins to ascend to the upper right on the Hertzsprung–Russell (H–R) diagram (red giant branch; Fig. 2). The He core increases its mass by the ash fall of He from the H-rich shell, and the core continues to contract. As a result, the core temperature rises sufficiently (10⁸ K) to result in the fusion of accumulated ⁴He, i.e., He burning. In He burning, three α (⁴He) particles react and produce ¹²C (triple-α process) as follows:

$${}^4\text{He}+{}^4\text{He}+{}^4\text{He}\to {}^{12}\text{C}+\mathrm{\gamma }$$

In some cases, especially in massive stars, ¹²C reacts with ⁴He and produces ¹⁶O via ¹²C(α, γ)¹⁶O. As a result, a C/O core is formed in the stellar center.

Figure 2.

Schematic evolution of a 1 M_☉ star with solar metallicity in the H-R diagram. Figure modified from Busso et al. (1999).

The subsequent scenario of nucleosynthesis is separated into two pathways depending on stellar mass. For low- to intermediate-mass stars (0.5–8 M_☉), the C/O core is lighter than the critical mass necessary to initiate the nuclear fusion of ¹²C (1.07 M_☉). The C/O core, thus, becomes increasingly dense and is supported by the pressure of degenerate electrons. Ultimately, He burning starts at the bottom of the He shell outside the C/O core, and the star ascends the asymptotic giant branch (AGB) pathway on the H–R diagram (Busso et al. 1999). The AGB phase is essential for producing many elements heavier than iron via the slow neutron capture process (s-process; see below). In the initial AGB phase, H burning occurs at the bottom of the H shell outside the He shell. As the He ashes accumulate on the He shell, the bottom of the He shell ignites explosively in a thermal pulse. The thermal pulse drives convection in the He shell and transfers materials in the He shell to the stellar surface, including the s-process nuclides.

As He and H shell burning continues in AGB stars, outer layers are eventually blown off by a strong stellar wind emitted by the star itself, leaving the central C/O core behind. The remaining electron-degenerate C/O core is called a “white dwarf”. When the white dwarf forms in a binary system, it can acquire H and He gas from the companion star and initiate explosive H burning on the surface, which is observed as a nova. The typical nucleosynthesis occurring in novae is explosive H burning, which produces ¹⁵N, ²²Na, and ²⁶Al via proton captures on CNO nuclei (e.g., Wiescher et al. 1986). If the white dwarf gains enough mass from the companion star to the level of the Chandrasekhar limit (~1.4 M_☉), then the stellar temperature and pressure increase sufficiently to initiate the fusion of C and O. This leads to a runaway reaction, releasing enormous energy and leading to stellar disruption (Type Ia supernova). Type Ia supernovae are extremely energetic such that C and O are fused into isotopes of Fe and Ni. Consequently, Type Ia supernovae are an important contributor of ⁵⁶Fe and other Fe-peak isotopes in galaxies.

Carbon Burning.

In the case of massive stars (>8 M_☉), the mass of the C/O core formed after central He burning becomes heavier than the critical mass to fuse ¹²C (> 1.07 M_☉). The C/O core continues to contract without electron degeneracy, and C burning initiates when the temperature reaches ~ 0.8 × 10⁹ K:

$${}^{12}\text{C}+{}^{12}\text{C}\to {}^{24}{\text{Mg}}^{*}$$

$${}^{24}{\text{Mg}}^{*}\to {}^{20}\text{Ne}+{}^4\text{He}$$

$${}^{24}{\text{Mg}}^{*}\to {}^{23}\text{Na}+{}^1\text{H}$$

$${}^{24}{\text{Mg}}^{*}\to {}^{24}\text{Mg}+\mathrm{\gamma }$$

where ²⁴Mg* is an excited state of ²⁴Mg. The dominant reaction of ²⁴Mg* decay produces ²⁰Ne, so that C burning is the principal contributor of ²⁰Ne in galaxies. The C shell burning starts when C in the core is exhausted. The C burning is the end stage of nuclear fusion for stars with masses ranging from 8 to 10 M_☉. In such cases, the core is lighter than the critical mass to fuse ²⁰Ne (1.37 M_☉), resulting in the formation of AGB stars with an electron degenerate O/Ne/Mg core, comparable to the case of low- to intermediate-mass stars. When AGB stars lose the envelope by stellar wind, the remaining core becomes a O/Ne/Mg white dwarf. The O/Ne/Mg white dwarfs can also produce novae in binary systems.

Neon Burning.

For stars with masses of > 10 M_☉, the O/Ne/Mg core continues to contract. When the core temperature reaches 1.5 × 10⁹ K, ²⁰Ne, the main product of C burning, starts to react as follows (Ne burning):

$${}^{20}\text{Ne}+\mathrm{\gamma }\to {}^{16}\text{O}+{}^4\text{He}$$

$${}^{20}\text{Ne}+{}^4\text{He}\to {}^{24}\text{Mg}+\mathrm{\gamma }$$

After consuming all of the ²⁰Ne, the ¹⁶O- and ²⁴Mg-rich core contracts and is characterized by increasing temperature until the next nuclear fusion process initiates (O burning).

Oxygen Burning.

The O burning occurs when the temperature of a stellar core reaches 1.5 × 10⁹ K following Ne burning. The nuclear reactions of O burning include:

$${}^{16}\text{O}+{}^{16}\text{O}\to {}^{32}{\text{S}}^{*}$$

$${}^{32}{\text{S}}^{*}\to {}^{28}\text{Si}+{}^4\text{He}$$

$${}^{32}{\text{S}}^{*}\to {}^{31}\text{P}+{}^1\text{H}$$

$${}^{32}{\text{S}}^{*}\to {}^{32}\text{S}+\mathrm{\gamma }$$

where ³²S* is an excited state of ³²S. The primary product of the O burning is ²⁸Si and ⁴He (α particle), as well as ³²S, forming a Si/S core after consumption of ¹⁶O.

Silicon Burning.

As the Si/S core continues to contract after O burning, photodisintegration of ²⁸Si occurs, which generates a supply of light particles (neutrons, protons, and ⁴He). Remaining ²⁸Si captures these light particles to make heavier species up to nickel. These nuclei all come into a state of equilibrium under exchange of the light particles (a quasi-statistical equilibrium). Due to their relatively high binding energies, the so-called alpha nuclei (³²S, ³⁶Ar, ⁴⁰Ca, ⁴⁸Cr, ⁵²Fe, and ⁵⁶Ni) dominate the abundances in equilibrium. Eventually, radioactive ⁴⁴Ti, ⁴⁸Cr, and ⁵²Fe, as well as ⁵⁶Ni (T_1/2 = 6.1 d), decay to ⁴⁴Ca, ⁴⁸Ti, ⁵²Cr, and ⁵⁶Fe, respectively, via electron capture.

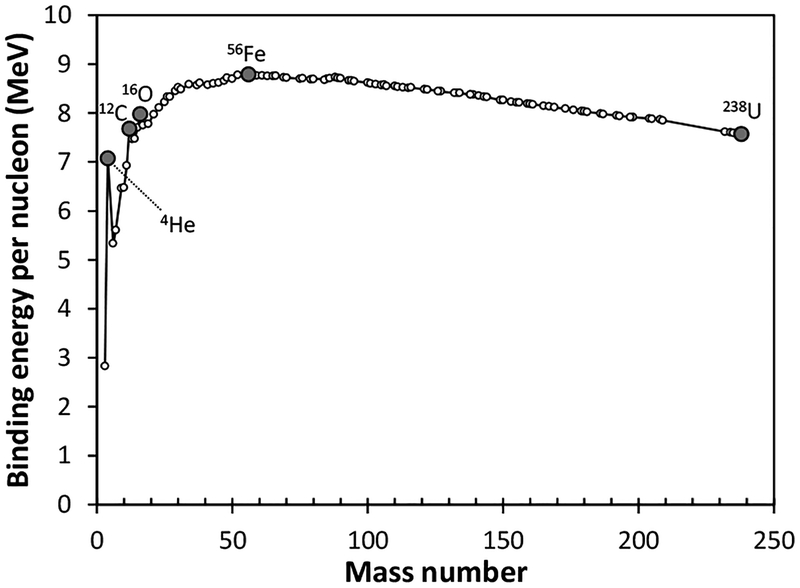
The binding energy per nucleon (E_b) as a function of mass number, E_b increases from low to intermediate mass nuclides with a peak top around mass number = 56 (Fig. 3; Ghahramany et al. 2012). The binding energy then decreases towards heavy nuclides, such as ²³⁸U. This implies that the nucleosynthesis of heavier nuclides, via α-capture, proceeds spontaneously, releasing their binding energies until the formation of ⁵⁶Ni. By contrast, the next reactions in which ⁵⁶Ni captures light particles (neutrons, protons, and ⁴He) are non-spontaneous as they do not release binding energy but consume energy. The silicon burning is sufficiently slow that at least some of the ⁵⁶Ni has time to decay into ⁵⁶Fe. Consequently, ⁵⁶Fe is the final nucleosynthetic product of the hydrostatic stellar evolution of massive stars. During Si burning in the stellar core, O-burning is proceeding in the shell enclosing the core, followed by Ne-, C-, He-, and H-burning proceeding from inner to outer shells. As a result, the star is made up of an “onion-skin” structure with several shells containing ashes of different nuclear fusion reactions in individual shells.

Figure 3.

Binding energy per nucleon (experimental values). Data source: Ghahramany et al. (2012).

At the end of hydrostatic stage of massive stars, all fuel is consumed in the core and the core begins to contract. At this point, Fe in the core disintegrates into protons, neutrons, and α-particles by absorbing gamma rays, leading to the collapse of the stellar core. Because of the high density in the collapsed core, protons capture electrons to convert to neutrons. Finally, the stellar center is crushed into either a neutron star, which is supported by the degeneracy pressure of neutrons, or a black hole when the star is sufficiently massive (> 30 M_☉). The outer layers of the star are blown off by the shock generated by the collapse of the core. This gravitational explosion is known as a core-collapse supernova (Type II, Ib, Ic). It should be noted that the designations Type II, Ib, Ic are spectroscopic. Type II supernovae are characterized by the presence of hydrogen in their spectra, while Type I’s do not. Of Type I supernovae, Ib’s are characterized by helium in their spectra, while neither helium nor silicon is present in the spectra of Ic’s. The shock also leads to some explosive burning in the inner layers of the original star. For instance, shock heating of the Si-rich layer causes explosive silicon burning, which produces Fe and Ni isotopes. Further, a neutron burst can occur during the explosive helium burning (Meyer et al. 2000).

Production of elements heavier than iron

As mentioned above, Fe and Ni are the final products of nucleosyntheses during hydrostatic stellar evolution. Because nuclear fusion of elements heavier than Fe is an endothermic reaction, more energetic and explosive nuclear burning is required for synthesizing heavier elements, including most of the siderophile and chalcophile elements. In the following, we introduce three important mechanisms for synthesizing elements heavier than Fe; the s-process, r-process and p-process. The s-process and r-process are neutron capture reactions which play a critical role in producing heavy elements. By contrast, the p-process is a reaction of either proton addition or photodisintegration, which produces minor proton-rich isotopes.

The s-process.

The s-process (slow neutron capture process) is a chain reaction of neutron capture and β^– decay, which proceeds relatively slowly with a timescale of thousands of years per single neutron capture. In the s-process, a seed nucleus with atomic number Z and mass number A captures a neutron and increases the mass number without changing the atomic number:

$$(\text{Z},\text{A})+\text{n}\to (\text{Z},\text{A}+1)$$

The next neutron capture occurs in 10³–10⁴ years, when the synthesized nucleus, (Z, A+1), is sufficiently stable:

$$(\text{Z},\text{A}+1)+\text{n}\to (\text{Z},\text{A}+2)$$

If the nucleus (Z, A+2) is radioactive, with a half-life significantly shorter than the timescale of neutron capture, then β^– decay occurs to produce a nucleus of higher atomic number, without changing the mass number:

$$(\text{Z},\text{A}+2)+\text{n}\to (\text{Z}+1,\text{A}+2)+{\text{e}}^{-}+{\overline{\mathrm{\nu }}}_e$$

where ${\overline{\mathrm{\nu }}}_e$ represents electron antineutrino.

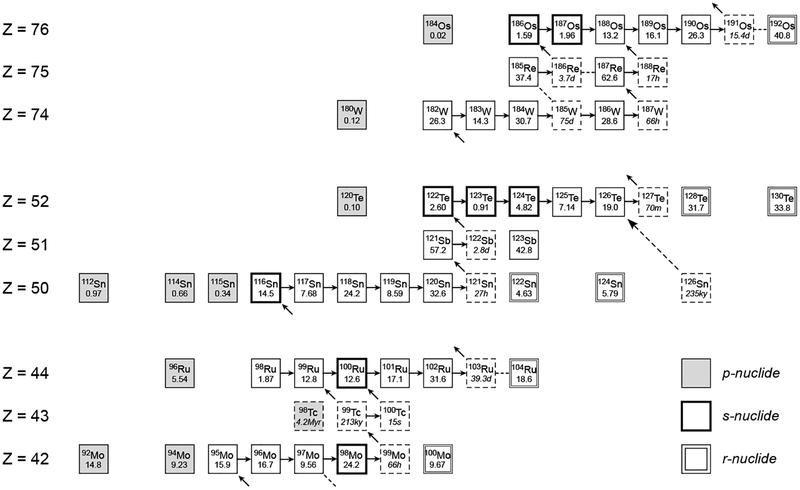
Examples of s-process pathways in the region from Mo to Ru, and from W to Os are shown in Figure 4. A box with a solid line refers to stable nuclides, and the number in the box is the Solar System isotopic abundance of the element (Böhlke et al. 2005). As shown in Figure 4, neutron capture repeats from ⁹⁴Mo to ⁹⁹Mo, the latter of which which decays to ⁹⁹Tc with a half-life of 66 h. The pathway is branched at the point of radioactive ⁹⁹Tc generation, because its half-life is sufficiently long that capture of another neutron is possible to create ¹⁰⁰Tc, while some portion of ⁹⁹Tc decays to ⁹⁹Ru. The pathways then meet at ¹⁰⁰Ru and neutron capture continues until the formation of the short-lived nuclide ¹⁰³Ru. In the s-process pathway, ⁹⁶Mo and ¹⁰⁰Ru are pure s-process nuclides because the formation of these nuclides, via the r-process, is shielded by stable isobaric nuclides of ⁹⁶Zr and ¹⁰⁰Mo (see below). By contrast, there exist some stable nuclides of Mo and Ru that cannot be produced by the s-process. Of such nuclides, proton-rich nuclides of ⁹²Mo, ⁹⁶Ru, and ⁹⁸Ru are produced only by the p-process, while the neutron-rich nuclides ¹⁰⁰Mo and ¹⁰⁴Ru are pure r-process isotopes.

Figure 4.

s-process pathways around Mo–Tc–Ru, Sn–Sb–Te, and W–Re–Os. Filled, bold, and double boxes are nuclides produced dominantly by the p-, s-, and r-processes. Dashed boxes are radioactive nuclides with their half-lives. Numbers in boxes are terrestrial abundances. Broken lines indicate minor path which may occur in specific conditions.

The s-process occurs in locations where the neutron density is relatively low such that the neutron capture process repeats every 10³–10⁴ years. To date, two stellar environments have been recognized as the sites for two different s-processes; the main s-process and the weak s-process (Käppeler et al. 1991, 2011).

The main s-process occurs in the He-burning shells of low-mass AGB stars, where free neutrons are produced via the following reaction to trigger the s-process:

$${}^{13}\text{C}+{}^4\text{He}\to {}^{16}\text{O}+\text{n}$$

The primary nuclide as the starting material of the s-process in AGB stars is ⁵⁶Fe, which was inherited from previous generations of stars. The main s-process pathway proceeds to form heavier nuclides and eventually reaches the final cycle, starting from ²⁰⁶Pb as follows:

$${}^{206}\text{Pb}+3\text{n}\to {}^{209}\text{Pb}\to {}^{209}\text{Bi}+{\text{e}}^{-}+{\overline{\mathrm{\nu }}}_e$$

$${}^{209}\text{Bi}+\text{n}\to {}^{210}\text{Bi}\to {}^{210}\text{Po}+{\text{e}}^{-}+{\overline{\mathrm{\nu }}}_e$$

$${}^{210}\text{Po}\to {}^{206}\text{Pb}+{}^4\text{He}$$

In this cycle, ²⁰⁶Pb captures neutrons and produces ²⁰⁹Bi via radioactive ²⁰⁹Pb (T_1/2 = 3.3 h). Further neutron capture forms radioactive ²¹⁰Bi (T_1/2= 5 d) which decays to ²¹⁰Po, followed by the α decay of ²¹⁰Po (T_1/2 = 138 d) which loops back to ²⁰⁶Pb. Therefore, ²⁰⁹Bi is the heaviest, long-lived nuclide (T_1/2 = 1.9 × 10¹⁹ y) that can be generated by the s-process, implying that another mechanism is required to produce heavier isotopes, such as ²³²Th and ²³⁸U.

By contrast, the weak s-process occurs as a result of He burning in the cores of massive stars, where free neutrons are supplied by the following process (Raiteri et al. 1993; Pignatari et al. 2010):

$${}^{22}\text{Ne}+{}^4\text{He}\to {}^{25}\text{Mg}+\text{n}$$

The weak s-process synthesizes s-process nuclides from an iron group seed nucleus up to the mass number A = 90 (Sr, Y).

The r-process.

The r-process (rapid neutron capture process) is a chain reaction in which successive neutron captures occur faster than the timescale of β-decays of neutron-rich nuclei generated, followed by the cascade of β-decays towards the zone of stable nuclei. The r-process occurs in stellar environments where the neutron density is sufficiently high to allow the formation of neutron-rich heavy nuclei via rapid neutron capture. This process is a major source of neutron-rich isotopes of various elements outside the s-process pathway (e.g., ¹⁰⁰Mo, ¹⁰⁴Ru). Also, the r-process generates long-lived heavy radioactive nuclides of ²³²Th, ²³⁵U, and ²³⁸U.

The production site of r-process nuclei is still debated. There are two promising sites for r-process synthesis: core-collapse supernovae (ccSN), and neutron star mergers. Of the ccSN models, nucleosynthesis in the neutrino-driven winds from protoneutron stars has been favored by many astrophysicists (e.g., Takahashi et al. 1994; Woosley et al. 1994; Wanajo et al. 2001). However, the neutrino-driven wind models contain the fundamental problem of unacceptable overproduction of some elements (e.g., Sr, Y, and Zr), relative to the Solar System elemental abundances. Moreover, recent numerical simulations have demonstrated that the neutrino-driven wind becomes proton-rich because of the interaction between neutron and neutrino (Fischer et al. 2009). Wanajo (2013) concluded that the neutrino-driven wind from protoneutron stars can be the source of light, trans-iron elements, but not for more than 10% of nuclei heavier than A = ~110 found in the Solar System.

In comparison, the merger of two neutron stars in a binary system has been proposed as an alternative scenario for r-process nucleosynthesis (e.g., Freiburghaus et al. 1999). Until recently, the neutron star mergers have not been accepted as a dominant r-process site because of their rarity of occurrence, and because the high yield of r-process elements per event would lead to r-process enrichment that is not consistent with observations of very low metallicity stars (Argast et al. 2004). However, Tsujimoto and Shigeyama (2014) observed a constant [Eu/H] (N.B., bracket represents the logarithm of the ratio of Eu/H value for a star compared to that of the Sun) in faint dwarf-spheroidal (dSph) galaxies, irrespective of their [Fe/H] values, whereas massive dSph galaxies are characterized by an increase of the [Eu/H] as [Fe/H] increases. Note that [Eu/H] and [Fe/H] are indices of r-process/hydrogen ratio and galactic chemical evolution, respectively. This observation implies that the r-process nucleosynthesis did not occur in faint dSph galaxies while supernovae frequently took place, as indicated by the increase of [Fe/H]. This would support neutron star mergers as the main source of r-process nuclides in our galaxy, especially for nuclides with A > 130 (Tsujimoto and Shigeyama 2014). Unlike red giants and supernovae, however, neutron star mergers do not condense dust grains as carriers of the r-process nuclides synthesized (cf. presolar grains). The mechanism how the r-process nuclides, synthesized by the neutron star mergers, were incorporated into the Solar System is still unclear. Therefore, one must keep in mind that the astrophysical site(s) for the r-process is very much an open question that will require further astronomical and theoretical investigation.

The p-process.

Proton-rich nuclei (e.g., ⁹²Mo, ⁹⁶Ru, ⁹⁸Ru, ¹²⁰Te, ¹⁸⁴Os) that depart from the s-process pathway cannot be produced by either the s-process or the r-process. The nucleosynthesis of such proton-rich nuclides is referred to as the p-process, in which three different types of processes occurring in various sites have been proposed; the rp-process, the γ-process, and the νp-process. Rauscher et al. (2013) provide a recent comprehensive review of the p-process.

The rp-process (rapid p-process) is a sequential reaction of successive proton capture and subsequent β⁺ decay. The rp-process requires an extremely proton-rich environment because (γ,p) reactions become faster than proton captures at high temperatures. The rp-process is thought to occur in explosive H- and He-burning on the surface of a mass-accreting neutron star, i.e., X-ray bursts (Schatz et al. 1998). However, there exists a definitive end point of the rp-process around A = 110, which prevents the synthesis of p-nuclei heavier than Te (Schatz et al. 2001).

The γ-process is a photodisintegration of pre-existing intermediate nuclei which produces lighter, proton-rich nuclei, either via successive (γ,n) reactions, or via (γ,p) or (γ,α) reactions, followed by β⁺ decays. The γ-process may have dominated over the rp-process in the production of p-nuclides for the Solar System (Rauscher et al. 2013). The primary site of the γ-process is core-collapse supernovae of massive stars, during which the shock front reaches the O/Ne-shell of the star where photodisintegration of preexisting s- and r-process materials occurs (e.g., Woosley and Howard 1978; Rauscher et al. 2002). One problem with the γ-process is that it underproduces the most abundant p-nuclei, ⁹²Mo, ⁹⁴Mo, ⁹⁶Ru, and ⁹⁸Ru, in the Solar System. To account for the deficits of ^92,94Mo and ^96,98Ru in the Solar System, an additional site for the γ-process, the Type Ia supernovae, has been proposed. Travaglio et al. (2011) explored the calculation of p-process nucleosynthesis for high-resolution two dimensional SNIa models, considering two types of explosions; delayed detonation and pure deflagration. The authors demonstrated that they could produce almost all p-nuclei at the same level as ⁵⁶Fe including the debated nuclides ^92,94Mo and ^96,98Ru, by assuming strong enhancements of s-process seed nuclides synthesized during the recurrence of thermal pulses during the white dwarf mass accretion phase. Travaglio et al. (2011) used a single degenerate (SD) scenario for the occurrence of Type Ia supernovae, in which mass accretion from a companion star onto a white dwarf reaches the Chandrasekhar mass and causes a supernova. On the other hand, a double degenerate (DD) scenario considered that the merger of two white dwarfs causes a supernova. The fraction of SD and DD types in actual type Ia supernovae remains unclear.

The third proposed p-process, the νp-process, is a neutrino-driven rp-process which occurs in the innermost ejected layers of a core-collapse supernova (ccSN) when intense neutrino fluxes create a proton-rich environment (Fröhlich et al. 2006; Pruet et al. 2006; Wanajo 2006). The standard rp-process is hindered during the ccSN, due to the existence of a number of “waiting points” such as ⁶⁴Ge (T_1/2= 1.06 m), where the timescale of β⁺ decay is sufficiently longer than the timescale of a ccSN (< 1 s). In the νp-process, the problem of waiting points can be resolved by accelerating the reactions via neutron capture and proton release, using neutrons produced by the absorption of antineutrino by protons (Wanajo 2006):

$$\text{p}+{\overline{\mathrm{\nu }}}_e\to \text{n}+{\text{e}}^{+}$$

$${}^{64}\text{Ge}+\text{n}\to {}^{64}\text{Ga}+\text{p}$$

The reactions occur within 1 s, so the waiting points are bypassed. The νp-process is a possible candidate for the origin of the solar abundances of ^92,94Mo and ^96,98Ru that cannot be explained by the γ-process.

PRESOLAR GRAINS

Since their discovery in the 1980s, a variety of presolar grains have been documented in primitive chondrites and interplanetary dust particles (IDPs). Different types of presolar grains have diverse isotopic compositions for various elements which are drastically different from one another, evidently indicating that they originated from multiple stellar environments where diverse nucleosyntheses occurred. In the last two decades, significant efforts have been made for direct isotopic measurement of single presolar grains, which has gradually clarified the linkage between individual presolar grains and their nucleosynthetic sources. Another approach to understanding the isotopic characteristics of presolar grains is the analysis of acid resistant residues and leachates extracted from primitive chondrites. The latter method is specifically useful when analyzing trace elements with concentrations of a few ppm in presolar grains. Collectively, these studies of presolar grains have revealed that much of the isotopic variability observed among bulk meteorites is nucleosynthetic in origin, and evidently caused by heterogeneous distribution of presolar grains in the solar nebula, prior to the onset of planetesimal formation. In this section, we review the history of presolar grain studies as well as the types of presolar grains discovered in chondrites and interplanetary dust grains.

Historical Background: Discovery and Isotope Analysis

Presolar grains are interstellar dust grains that existed before the formation of the Solar System. Presolar grains reside in primitive meteorites, especially in the matrix of carbonaceous chondrites that have been minimally affected by thermal metamorphism on their parent bodies. In addition to carbonaceous chondrites, presolar grains have also been found in ordinary and enstatite chondrites. Presolar grain abundances comprise typically no more than 0.1% of the mass of an individual meteorite (e.g., Nguyen and Messenger 2011; Zinner 2014). Presolar grains contained in meteorites and interplanetary dust grains are remnants of the ingredients that made up the Solar System. These ingredients formed in a variety of stellar environments. Further, the existence of presolar grains in chondrites implies that these grains have survived dynamical processes in the early solar nebula, such as evaporation, condensation, mixing and collision. Since these grains are labile at high temperature, chondrites that were affected by higher degrees of thermal metamorphism (e.g., petrologic grade greater than 3.6), and differentiated meteorites that experienced melting on their parent bodies (e.g., achondrites, iron meteorites, stony-iron meteorites) no longer carry presolar grains.

The existence of presolar materials was predicted before their discovery (Clayton 1978). As summarized in the previous section, current nucleosynthetic models suggest all elements heavier than He were synthesized by a variety of stellar environments as stellar evolution in the universe proceeded. Since nucleosynthesis in different stellar environments would produce elements with different isotopic compositions, it was projected that such putative “presolar components” should have isotopic compositions drastically different from those of terrestrial composition (Clayton 1978). However, due to a lack of evidence for resolvable nucleosynthetic anomalies among bulk planetary materials, it was originally concluded that the inner part of the early solar system experienced sufficiently high temperatures that all solid materials were evaporated and ultimately mixed, such that the isotopic compositions of all elements in accessible planetary materials were thoroughly homogenized.

The improvement of mass spectrometers and associated techniques in the 1960–70s led to the discovery of isotopic anomalies in meteorites and their components (Reynolds and Turner 1964; Black and Pepin 1969; Lewis et al. 1975; McCulloch and Wasserburg 1978a,b; Papanastassiou and Wasserburg 1978). Because these measurements were made on chemically processed, bulk planetary materials, however, these studies were incapable of identifying the carriers of the isotopically anomalous components. Finally, in the 1980s, the group of E. Anders from the University of Chicago examined the residues of stepwise acid leaching from primitive chondrites, and measured their rare gas isotopic compositions. They discovered that the fraction showing an anomalous Xe isotope composition (Xe-HL) is composed of acid insoluble, presolar nanodiamonds. This is considered the first discovery of presolar grains (Lewis et al. 1987). Subsequently, the group discovered presolar silicon carbide (carrier of Xe-S and Ne-E(H)), and presolar graphite (carrier of Ne-E(L)) (Bernatowicz et al. 1987; Amari et al. 1990).

The study of individual presolar grains has dramatically improved since the 1980s as a result of the development of secondary ion mass spectrometry (SIMS), which enables direct isotopic analysis of an area of 10 μm diameter or less. In SIMS analysis, the sample of interest is put in a sample chamber that is under vacuum, without prior chemical separation. The targeted area for isotopic analysis is sputtered by a focused primary beam (e.g., Cs⁺, O^–) to generate secondary ions that are focused and separated by their mass/charge ratios, using the electrostatic analyzer and magnetic sector that follow the ion source. The analytical targets for SIMS measurements are typically major element constituents of presolar grains, such as C, O, and Si, as well as some minor elements lighter than Fe (e.g., N, Mg, Ca, and Ti). The analytical uncertainties depend on various conditions; however, those of major elements are normally less than a few % in general.

A major drawback of SIMS analysis is the difficulty of isotope analysis for elements heavier than Fe. Resonance ionization mass spectrometry (RIMS) is an alternative analytical technique which has played an important role in obtaining the isotopic compositions of some heavy elements in presolar grains, including some siderophile elements (e.g., Mo, Ru: Nicolussi et al. 1998a,b; Savina et al. 2004). In RIMS analysis, a sample volume is sputtered using a conventional ion probe gun. The cloud of neutral and charged particles resulting from the sputtering is then interrogated by irradiating the cloud with laser beams with wavelengths tuned to achieve the excitation energy level necessary to selectively photoionize the target element. The isotopic composition of the element is then measured by time of flight mass spectrometry. This method enables selective ionization of the target element without chemical separation from unwanted elements which, if ionized, could result in isobaric interferences with the element of interest. (e.g., CHARISMA, Argonne National Laboratory: Savina et al. 2003).

Types of Presolar Grains and Their Origin

Table 1 summarizes the types of presolar grains discovered in meteorites and interplanetary dust particles (IDPs) to date. Microscopic images of representative presolar grains are shown in Figure 5. In the following, we briefly review the nucleosynthetic origin of each type of presolar grain. For the isotope data presented in some Figures, we take data from the database for presolar grains created by (Hynes and Gyngard 2009).

Table 1.

Abundances, sizes, and stellar sources of presolar grains.

Grain type	“Abundance (ppm)”	“Size (μm)”	Stellar sources
Nanodiamonds	1000	0.002	SNe
SiC	40	0.1–20	AGB, SNe, Novae, J-stars
Graphite	2	1–20	SNe, AGB
Oxides	100	0.1–3	RG, AGB, SNe
Silicates (IDPs)	15000	0.1–1	RG, AGB, SNe
Silicates (meteorites)	200	0.1–1	RG, AGB
Si3N4	0.002	0.3–1	SNe

Presolar grain abundances vary with meteorite type.

Figure 5.

Images of presolar grains. (a) nanodiamond (b) SiC (c) graphite, and (d) corundum. Used by the following permission. (a) Tyrone L. Daulton, Washington University in St. Louis (b) Scott Messenger, NASA (c) Sachiko Amari, Washington University in St. Louis (d) Aki Takigawa, Kyoto University.

Nanodiamond.

As described previously, nanodiamonds (Fig. 5a) were the first type of presolar grain discovered in chondrites. The existence of nanodiamond was confirmed by using X-ray diffraction (XRD) and transmission electron microscopy (TEM) analysis. The abundance of nanodiamonds in chondrites can be as much as 0.1% of the mass. Direct isotope analysis of single nanodiamond grains is currently impossible because of their minuscule grain size. Therefore, isotope compositions of nanodiamond grains have been obtained by group analysis of nanodiamond-enriched acid residues extracted from chondrites. However, the origin of this type of presolar grain is still controversial. As described above, rare gas isotope results on the nanodiamond-enriched fractions provided the first evidence that at least some portion of the nanodiamonds present are interstellar dust grains, which record the collective isotopic compositions of the materials present in their formation environment (Lewis et al. 1987). Excesses of Te and Pd isotopes (¹²⁸Te, ¹³⁰Te, and ¹¹⁰Pd) have also been reported for nanodiamond-enriched fractions extracted from a carbonaceous chondrite (Richter et al. 1998; Maas et al. 2001). These characteristics can be produced by an intense neutron-burst when a supernova shock heats the He-burning shell and liberates neutrons via ²²Ne(α,n)²⁵Mg (Meyer et al. 2000). More recently, Stroud et al. (2011) analyzed nanodiamond separates from the Allende and Murchison meteorites using electron microscopy with sub-nanometer resolution. The authors demonstrated that the separates were a two-phase mixture of nanodiamonds and glassy carbon, which was most likely the product of supernova shock-wave transformation of pre-formed organics in the interstellar medium. By contrast, Dai et al. (2002) found that fragile, carbon-rich IDPs of cometary origin are nearly free of nanodiamonds, suggesting that nanodiamonds in meteorites formed within the inner Solar System and are not presolar. The inconsistency may imply that the majority of nanodiamonds originated in the Solar System. Nevertheless, at least a small proportion of nanodiamonds are undoubtedly presolar and record nucleosynthetic anomalies.

Silicon carbide.

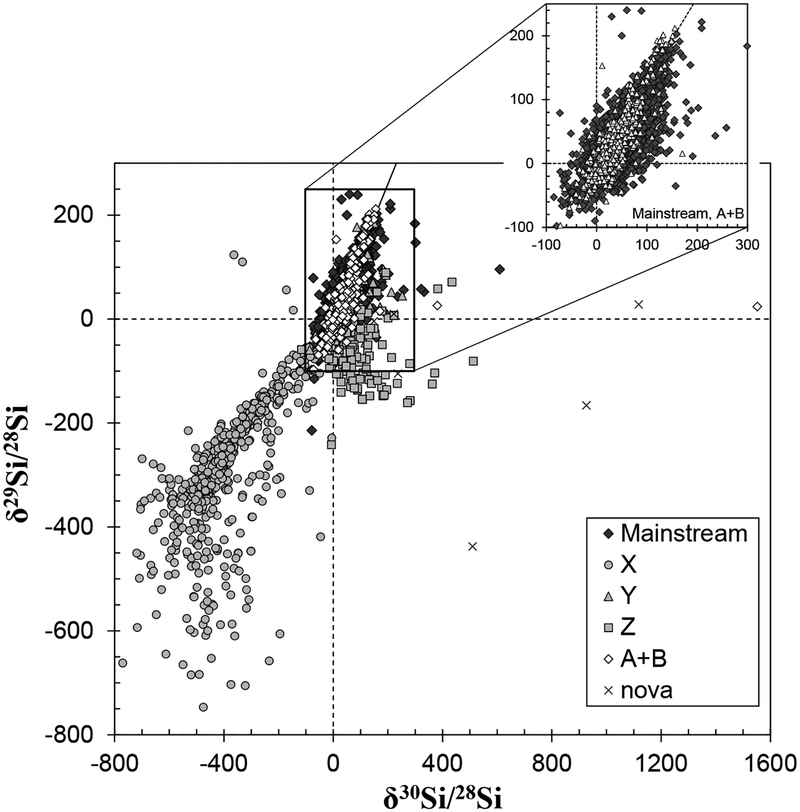
The maximum abundance of SiC in chondrites is 30–40 ppm (Davidson et al. 2014). SiC (Fig. 5b) is strongly acid resistance, however, so that the separation of presolar SiC from other meteorite components is possible by a stepwise acid leaching procedure. Since SiC does not form by nebular processes, SiC grains observed in chondrites are all presumed to be presolar in origin. Typical SiC grains occur at a μm scale. Therefore, it is possible to perform direct isotopic analysis of this type of grain using SIMS. Consequently, SiC is the most studied presolar grain among all types of presolar materials. Comprehensive analysis of Si, C, and N isotope compositions in presolar SiC grains has revealed that presolar grains can be divided into several groups of different nucleosynthetic origin. More than 90% of presolar SiC is categorized as mainstream SiC, and the rest are separated into subgroups of A + B, X, Y, Z, and Nova.

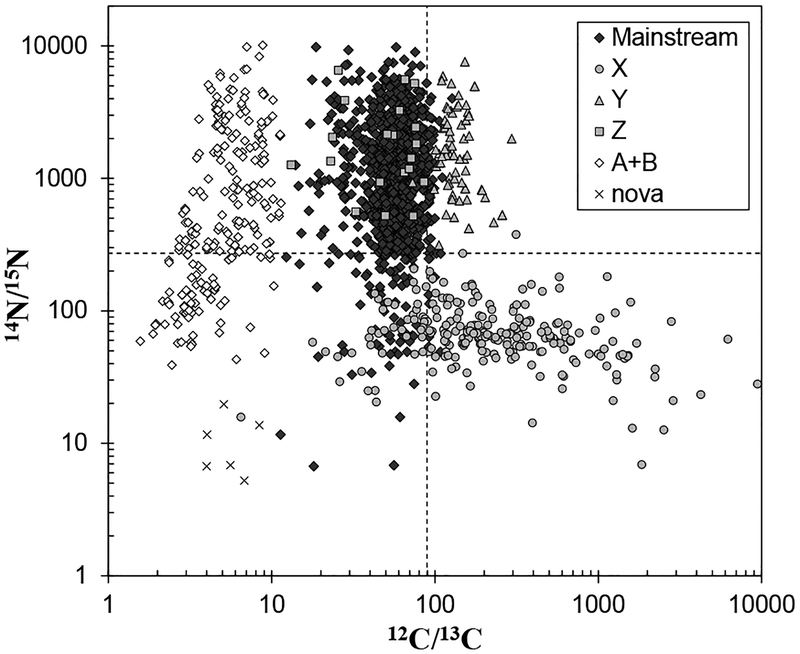
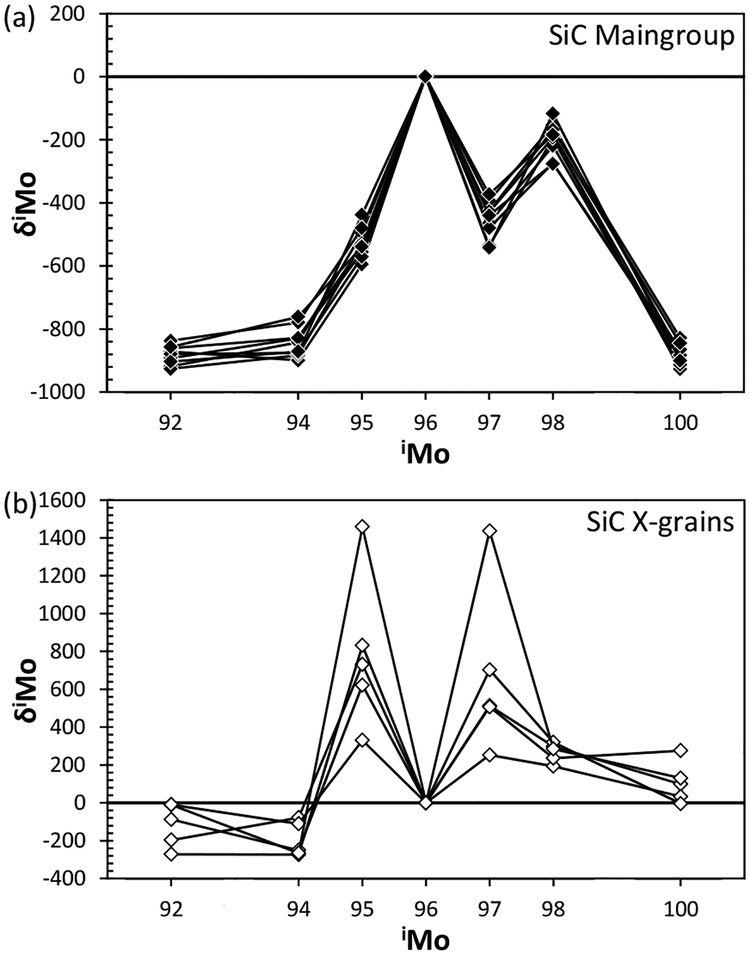
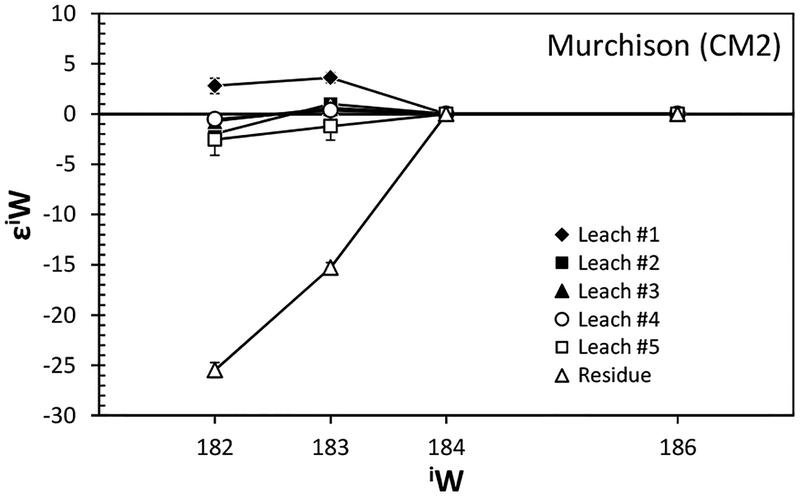
The mainstream SiC grains are characterized by higher ^29,30Si/²⁸Si and ¹⁴N/¹⁵N ratios, and lower ¹²C/¹³C ratios, compared to those of terrestrial values (Figs. 6–7). Carbon isotope ratios, as revealed by the analysis of mainstream SiC grains, are consistent with the ¹²C/¹³C ratio observed in carbon stars, which are AGB stars as discussed in earlier section (Lambert et al. 1986). In addition, an infrared emission feature around 11.3 μm observed in the outflows of carbon stars points to the existence of SiC particles (Speck et al. 1997). Based on these observations, and the comparison of C and N isotopic compositions in SiC with nucleosynthetic theories, the mainstream SiC grains, as well as Y and Z grains, are concluded to originate from low-mass carbon stars (1–3 M_☉) (e.g., Zinner et al. 1989; Alexander 1993; Hoppe et al. 1994; Nittler and Alexander 2003). Isotope analyses of heavy elements in individual mainstream SiC grains using RIMS or SIMS discovered large excesses of s-process nuclides, such as ^86,87Sr, ⁹⁶Mo,^90,91,92,94Zr, ¹⁰⁰Ru, and ^134,136Ba (Fig. 8) (Nicolussi et al. 1998a; Savina et al. 2004; Barzyk et al. 2007; Liu et al. 2014). Likewise, enrichments of s-process nuclides in chondritic acid residues containing presolar SiC grains were observed for a variety of elements, including the siderophile elements Mo, Ru, W, and Os (Dauphas et al. 2002b; Yokoyama et al. 2007, 2010, 2011; Burkhardt et al. 2011, 2012a). These results are consistent with the nucleosynthetic theory that s-process occurs in the He-burning shell of low-mass AGB stars.

Figure 6.

Silicon isotopic compositions of presolar silicon carbide grains. The presolar grain database by Hynes and Gyngard (2009) was used to plot the data. The original sources of representative data are Alexander (1993), Alexander and Nittler (1999), Amari et al. (2001a, 2001b, 2001c), Barzyk et al. (2007), Besmehn and Hoppe (2003), Hoppe et al. (1994, 1996), Huss et al. (1997), Lin et al. (2002), Marhas et al. (2008), Nittler and Alexander (2003), Virag et al. (1992), and Zinner et al. (2003, 2007). The full references for the entire data suite are available in Hynes and Gyngard (2009).

Figure 7.

Carbon and nitrogen isotopic compositions of presolar silicon carbide grains. Dashed lines are those of solar system average. Data are from the same sources as for Figure 6.

Figure 8.

Representative data for Mo isotope compositions in (a) mainstream SiC grains and (b) type X SiC grains. Data are from Barzyk et al. (2007) and Pellin et al. (2006).

Type X SiC grains are rare, comprising only ~1% of the abundance of all SiC grains analyzed. These grains can be distinguished from the mainstream grains with their lower ^29,30Si/²⁸Si and ¹⁴N/¹⁵N ratios and higher ¹²C/¹³C ratios (Figs. 6–7). The origin of X grains is most likely the ejecta of core collapse supernovae, because some X grains are enriched in ⁴⁴ Ca and ⁴⁹Ti, both of which are daughter nuclides of short-lived radioactive nuclides synthesized only in ccSNe (⁴⁴Ti and ⁴⁹V, respectively). By contrast, RIMS measurements of X grains discovered excesses of ⁹⁵Mo and ⁹⁷Mo (Fig. 8) (Pellin et al. 2006). Interestingly, the Mo isotopic pattern observed in the X grains does not match any patterns produced by conventional three nucleosynthetic models (s-, r-, and p-processes). Rather, the pattern is consistent with a formation mechanism via the neutron burst that takes place in a He-shell during passage of the supernova shockwave (Meyer et al. 2000; Rauscher et al. 2013). The importance of these X-grain measurements is that they show the existence of additional nucleosynthetic components, other than those synthesized via the s-, r-, and p-processes, the main nucleosynthetic sources for trans-iron elements. Such components may not play a significant role in the overall composition of the Solar System, but would be present in individual presolar carriers, and thus, could influence isotopic variations in early Solar System materials. The neutron burst model also accounts for the isotopic composition of Te and Pd in nanodiamonds (see above).

Isotopic analyses of the other minor types of SiC grains are limited. The Nova grains, originated from the explosive H burning of novae, have lower ¹²C/¹³C and ¹⁴N/¹⁵N ratios and higher ³⁰Si/²⁸Si and ²⁶Al/²⁷Al ratios relative to the terrestrial values (Figs. 6–8) (Amari et al. 2001a). The type A + B grains possess Si isotope compositions similar to the mainstream grains but have extremely low ¹²C/¹³C ratios and variable ¹⁴N/¹⁵N ratios (Amari et al. 2001b). These isotopic signatures cannot be explained by nucleosynthesis in normal AGB stars. Amari et al. (2001b) proposed that a possible source of A + B grains with enhanced s-process elemental abundances was born-again AGB stars, which are post AGB stars in late thermal pulse phase due to the re-ignition of the He shell surrounding the C/O core (Sakurai’s object). An alternative source of the A + B grains are the J-type carbon stars, which have extremely low ¹²C/¹³C ratios, although the details of such a model are still unclear (Amari et al. 2001b). In addition, excesses of p-process isotopes ^92,94Mo and ^96,98Ru were reported in a type B SiC grain (Savina et al. 2007), which would require at least one more nucleosynthetic source for this type of grain.

Graphite.

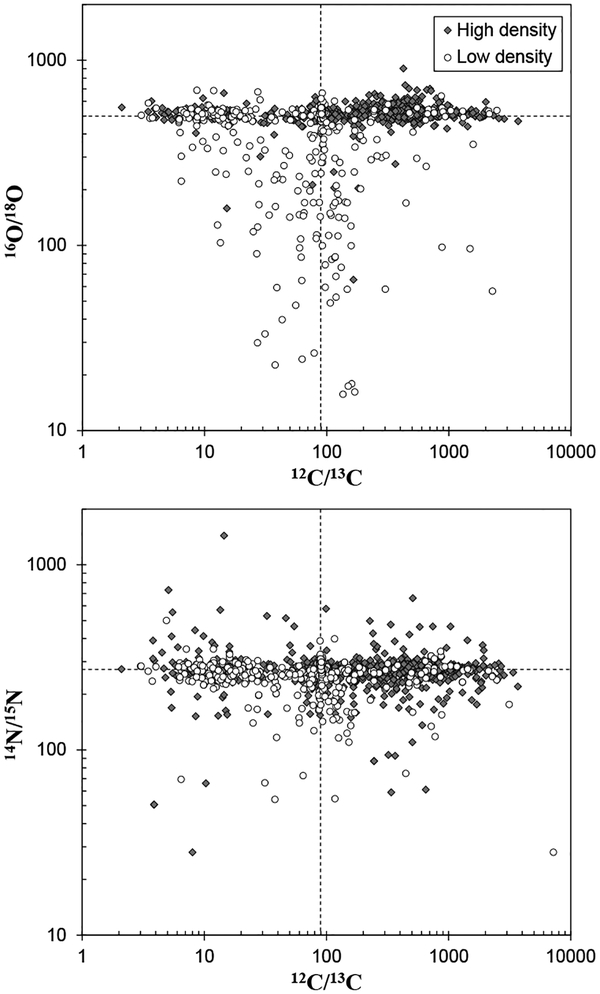
The abundance of presolar graphite in chondrites (Fig. 5c) reaches a maximum of ~2 ppm. The grain size of the presolar graphite ranges from 1 to 20 μm. The density of presolar graphite is bimodal; the more grain sizes increase, the more the density of grains decreases. Because of their distinctive isotopic characteristics, the stellar origin of the low density (LD) graphite and high density (HD) graphite is thought to be different from each other.

The ¹²C/¹³C ratios of HD graphite grains range from 2 to 4000 with bimodal peaks around ¹²C/¹³C = 10 and 300–400 (Fig. 9). Amari et al. (2014) investigated presolar graphite grains separated from the Murchison meteorite and concluded that HD grains of 2.10–2.15 g·cm^–3 with ¹²C/¹³C ≥ 100 formed in the outflow of low-mass (1.5–3 M_☉) and low-metallicity AGB stars, and those of 2.15–2.20 g·cm^–3, with ¹²C/¹³C ≥ 60 formed in the same stars, as well as in 5M_☉ and solar to half-solar metallicities. Such environments are markedly different from the site where the mainstream SiC grains formed. In contrast, the HD grains with ¹²C/¹³C ≤ 20 have multiple origins including the ejecta of ccSN, J stars, and born-again AGB stars. Another intriguing signature is that some of the HD graphite grains contain tiny refractory carbide grains (e.g., ZrC, MoC, and RuC) at the center as a subgrain (Bernatowicz et al. 1996; Croat et al. 2005). The sub-grains evidently existed prior to the crystallization of graphite grains, which provide a clue to understanding the formation process of presolar grains in the stellar envelope. Because Zr, Mo, and Ru are dominantly s-process elements, the existence of refractory subgrains supports the AGB origin of the HD graphite grains. Nicolussi et al. (1998b) measured Zr and Mo isotope compositions in 32 individual HD graphite grains from the Murchison meteorite using RIMS. Although most of the grains showed close-to-terrestrial Mo isotopic compositions, five grains had Mo isotopic patterns with excess s-process nucleosynthetic signatures. In addition, three out of eight graphite grains for which Zr and Mo isotope compositions were measured simultaneously presented correlated s-process isotopic characteristics for both Zr and Mo, suggesting low-mass, thermally pulsed AGB stars as their origin.

Figure 9.

Carbon, nitrogen, and oxygen isotopic compositions of presolar graphite grains. Dashed lines are those of solar system average. The presolar grain database by Hynes and Gyngard (2009) was used to plot the data. The original sources of representative data are Amari et al. (1993), Hoppe et al. (1995), and Jadhav et al. (2013). The full references for the entire data are available in Hynes and Gyngard (2009).

On the other hand, the LD graphite grains (2.05 g·cm^–3) possess trace element abundances higher than HD graphite. LD graphite is characterized by excesses of ¹⁵N, ¹⁸O, ²⁸Si, as well as high ²⁶Al/²⁷Al ratios. The distribution of ¹²C/¹³C shift to lower ratios compared to HD graphite, with a peak around ¹²C/¹³C = 90–200. These isotopic signatures resemble those of SiC X grains, the origin of which is most like ccSNe. The ccSN origin of LD graphite is supported by excesses of daughter nuclides of the short-lived radionuclides ⁴⁴Ti and ⁴¹Ca. These nuclides are produced by neutron capture in the C/O-shell of type II supernovae, although ⁴⁴Ti and ⁴¹Ca are also produced by the oxygen and silicon burning, and by the weak s-process in convective core helium burning, respectively.

Oxides and Silicate.

Presolar corundum (Al₂O₃) is the grain first discovered as a carbon-free mineral (Fig. 5d). Presolar oxides identified other than corundum are spinel (MgAl₂O₄), hibonite (CaAl₁₂O₁₉), TiO₂, FeO, and FeCr₂O₄. The maximum abundance of presolar oxides in chondrites is ~100 ppm. The grain size of presolar oxides ranges from 0.1 to 3 μm in diameter. Unlike SiC, oxide grains can be formed by a variety of nebular processes and are abundant in the Solar System. Therefore, the only way to identify presolar oxides in chondrites is the direct isotope analysis for oxygen using SIMS.

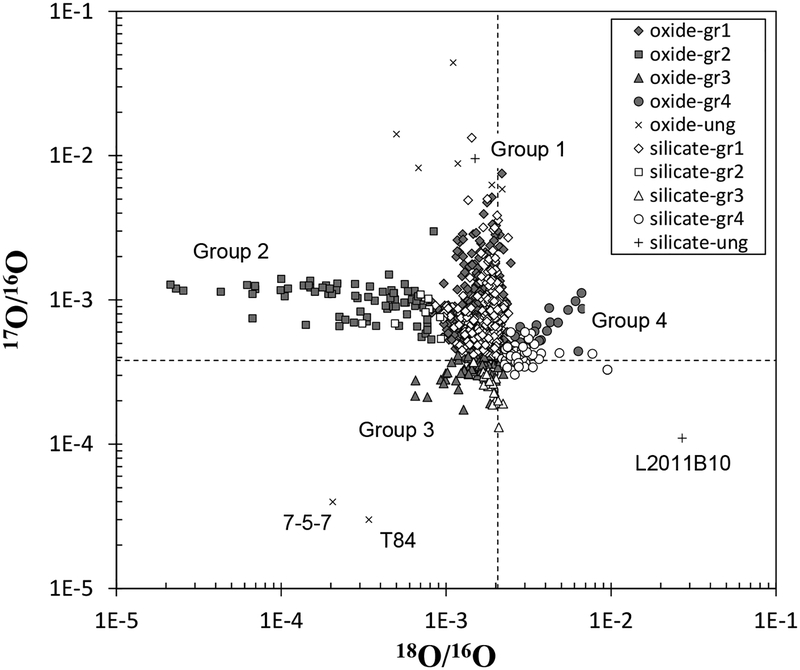
Identification of presolar silicates has been hampered by the fact that silicates are not acid resistant, especially to HF. In addition, silicates are the most abundant types of minerals in the Solar System that formed in the nebula. The first discovery of presolar silicates was in interplanetary dust particles (Messenger et al. 2003). The abundance of presolar silicates in IDPs reaches ~1%, which is the greatest among all types of presolar grains. Subsequently, presolar silicates were discovered in chondrites by SIMS analysis (Nagashima et al. 2004; Nguyen and Zinner 2004). The abundance of presolar silicates in chondrites is a maximum of ~ 250 ppm. The presolar silicates that have been identified include forsterite, enstatite, Ca–Al-rich phases, and non-stoichiometric amorphous silicates with grain size ranging from 0.1–1 μm. Based on O isotopic compositions, Nittler et al. (1997) categorized presolar oxide grains into four groups with different stellar origins. The same groupings are applied to presolar silicate grains.

As shown in Figure 10, Group 1 grains are enriched in ¹⁷O and have ¹⁸O/¹⁶O ratios slightly lower than the Solar System average. This is consistent with those observed in red giant and AGB stars. Group 2 grains have significant deficits in ¹⁸O (¹⁸O/¹⁶O < 0.001) with ¹⁷O/¹⁶O ratios slightly higher than the Solar System average. The deficits of ¹⁸O are difficult to explain with first and second dredge-ups in red giant stars, however, the mixing of materials from the envelope into the H-burning shell (cool bottom processing) that occurs in low mass (< 1.65 M_☉) AGB stars may explain the observed isotopic compositions. Group 3 has ¹⁷O/¹⁶O and ¹⁸O/¹⁶O ratios lower than the Solar System average. This can be explained by the gradual increase of secondary nuclides ¹⁷O and ¹⁸O, relative to the primary nuclide ¹⁶O, along with galactic chemical evolution (GCE), indicating that Group 3 grains originated from low mass and low metallicity stars. The origin of Group 4 grains has been debated. Although these grains are enriched in ¹⁷O and ¹⁸O relative to ¹⁶O, they do not show excesses of ²⁹Si and ³⁰Si relative to ²⁸Si, which is inconsistent with the GCE model. An alternative interpretation for the origin of Group 4 grains is a single supernova (Choi et al. 1998; Nittler et al. 2008).

Figure 10.

Oxygen isotopic compositions of presolar oxide and silicate grains. Dashed lines are those of solar system average. The presolar grain database by Hynes and Gyngard (2009) was used to plot the data. The original sources of representative data are Bose et al. (2010), Choi et al. (1998, 1999), Floss and Stadermann (2009), Gyngard et al. (2010), Mostefaoui and Hoppe, (2004), Nagashima et al. (2004), Nguyen et al. (2003), Nguyen and Zinner (2004), Nguyen et al. (2007, 2010), Nittler et al. (1997, 2008), Vollmer et al. (2009a, 2009b), and Zinner et al. (2003, 2005). The full references for the entire data are available in Hynes and Gyngard (2009).

To date, no isotopic data are available for trace elements heavier than iron in presolar oxide and silicate grains. New generations of mass spectrometers with extremely high sensitivity will be required to shed light on the isotopic characteristics of trace elements, including siderophile and chalcophile elements, in this group of presolar grains.

Silicon Nitride.

Silicon nitride (Si₃N₄) is one of the rarest presolar grains. The isotopic characteristics of Si₃N₄ grains resemble those of SiC X grains, suggesting a supernova origin. However, one Si₃N₄ grain was found in the enstatite chondrite Indarch. It was characterized by excesses of ¹³C and ¹⁴N, and likely originated from an AGB star (Zinner et al. 2007).

ISOTOPE ANOMALIES OF SIDEROPHILE AND CHALCOPHILE ELEMENTS IN BULK METEORITES

The extent and causes of isotopic heterogeneity in the early Solar System have been long-standing issues since the establishment of nucleosynthetic models and the discovery of presolar grains. The existence of presolar grains in chondrites and interplanetary dust particles (IDPs) implies that the original dust grains present in the solar nebula were not completely evaporated before the onset of planetesimal formation. Heterogeneous distribution of isotopically anomalous presolar grains in the solar nebula would cause isotopic anomalies among planetary bodies that formed separately in time and space. Therefore, investigating nucleosynthetic isotopic anomalies in a variety of meteorites is of great importance for understanding large-scale material transport and subsequent nebular and planetary processes.

In the following section, we review recent achievements in the precise measurement of the isotopic compositions of siderophile and chalcophile elements in bulk aliquots of meteorites, including chondrites and differentiated meteorites. We specifically focus on trans-iron elements which are generally synthesized by the stellar nucleosyntheses of the s-, r-, and p-processes. A specific emphasis is made here on studies after ~2000, in which high precision isotope measurements were employed with analytical uncertainties of epsilon level (part per 10,000) or better. Such high precision isotope analyses are not available for all siderophile and chalcophile elements, and are presently limited to Mo, Ru, Te, W, and Os. The variation of isotope compositions for these elements in bulk meteorites are summarized in Table 2 for representative references. We will review observations regarding these elements, and also highlight advancing work on Pt and Cd isotopes.

Table 2.

Variation of isotope compositions for Mo, Ru, Te, W, and Os in bulk meteorites and terrestrial standards.

	Chondrites			Non-chondrites			Terrestrial Std
	Carbonaceous	Ordinary	Enstatite	Achondrites	Irons	Stony irons
	min-max	min-max	min-max	min-max	min-max	min-max	± 2σ
Molybdenum
ε92Mo/96Mo	1.12 to 6.44	0.58 to 0.94	0.36 to 0.65	−0.14 to 0.52	−0.23 to 1.99	1.06 to 1.14	0 ± 0.75
ε94Mo/96Mo	0.00 to 4.82	0.43 to 1.01	0.30 to 0.61	0.09 to 0.69	−0.31 to 1.42	0.85 to 0.85	0 ± 0.50
ε95Mo/96Mo	0.53 to 3.17	0.12 to 0.38	0.18 to 0.19	−0.12 to 0.06	−0.19 to 1.02	0.38 to 0.80	0 ± 0.41
ε97Mo/96Mo	0.12 to 1.66	0.09 to 0.18	0.11 to 0.14	0.02 to 0.20	−0.15 to 0.53	0.16 to 0.41	0 ± 0.23
ε100Mo/96Mo	0.35 to 2.28	0.04 to 0.37	0.12 to 0.31	−0.14 to 0.40	0.00 to 0.91	0.20 to 0.79	0 ± 0.44
References	[1]	[1]	[1]	[1]	[1]	[1]	[1]
Ruthenium
ε96Ru/101Ru	0.13 to 1.41	−0.01 to 1.38			−0.58 to 0.82	0.2 to 0.45	0 ± 1.19
ε98Ru/101Ru	0.34 to 2.94	−0.84 to 2.44			−0.42 to 1.79	0.25 to 1.56	0 ± 1.98
ε100Ru/101Ru	−1.70 to 0.60	−0.26 to 0.44			−1.08 to 0.00	−0.58 to −0.36	0 ± 0.31
ε102Ru/101Ru	−0.29 to 0.81	−0.43 to 0.45			−0.53 to −0.05	−0.03 to 0.15	0 ± 0.64
ε104Ru/101Ru	0.58 to 1.65	−0.45 to 0.55			−0.44 to 0.52	−0.19 to 0.37	0 ± 0.58
References	[2]	[2]			[2]	[2]	[2]
ε100Ru/101Ru	−3.37 to −1.00	−0.30			−1.1 to −0.33
ε102Ru/101Ru	−1.25 to −0.39	−0.14			−0.462 to −0.04
References	[3]	[3]			[3]
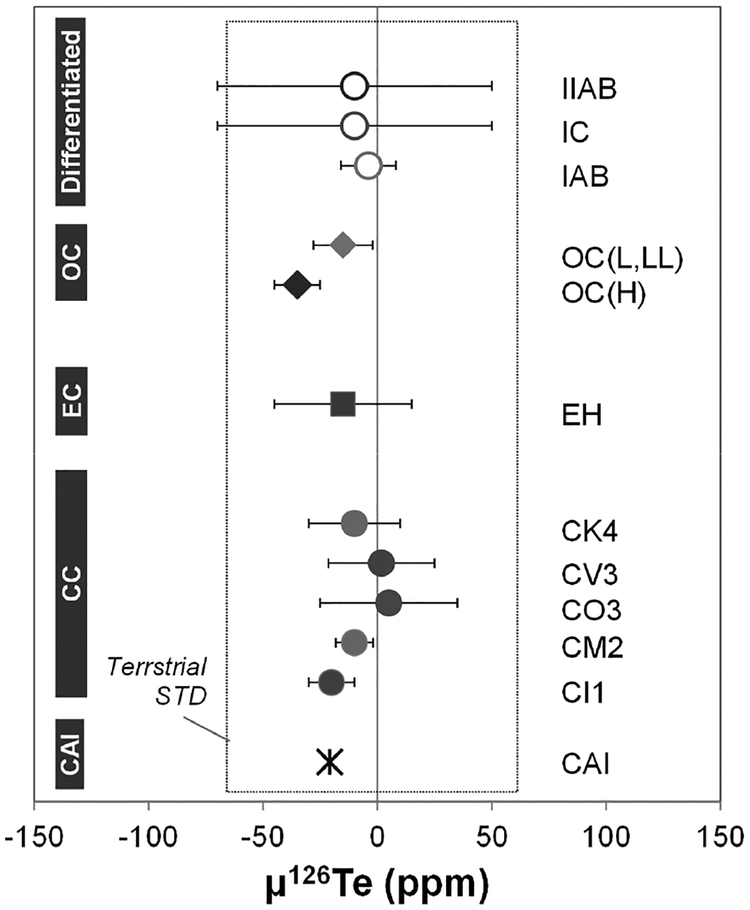
Tellurium
ε120Te/128Te	−26 to 39	−49 to 16	2		−39 to 49		0 ± 45
ε122Te/128Te	−2.2 to 1.9	−2.3 to −0.5	−1.4		−1.2 to 4.5		0 ± 1.4
ε124Te/128Te	−1.0 to 0.3	−1.9 to −0.4	−0.10		−0.5 to 1.8		0 ± 1.0
ε126Te/128Te	−0.3 to 0.4	−0.4 to 0.0	−0.3 to 0.0		−0.3 to 0.3		0 ± 0.3
ε130Te/128Te	−0.4 to 0.9	0.3 to 0.9	0.5 to 0.9		−1.5 to 0.7		0 ± 0.6
References	[4]	[4]	[4]		[5]		[4]
Tungsten
ε183W/184W	−0.47 to 0.54			−0.43 to 0.43	−0.16 to 0.09		0 ± 0.77
References	[6]			[6]	[6]		[6]
ε184W/183W					−0.15 to 0.01		0 ± 0.05
References					[7]		[7]
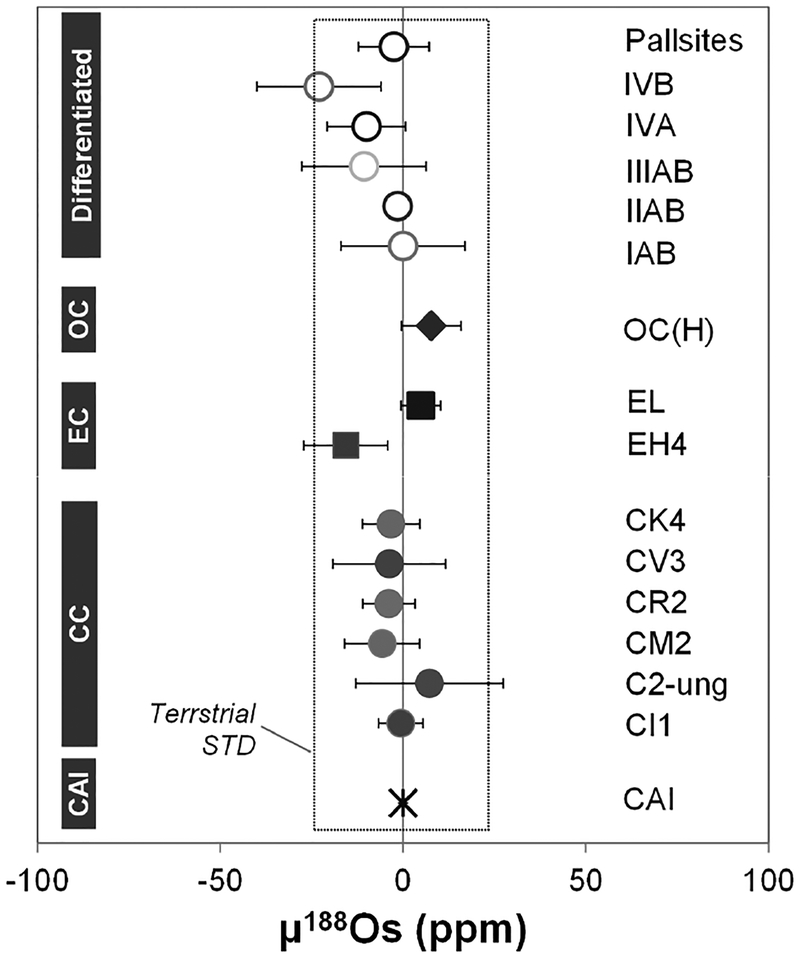
Osmium
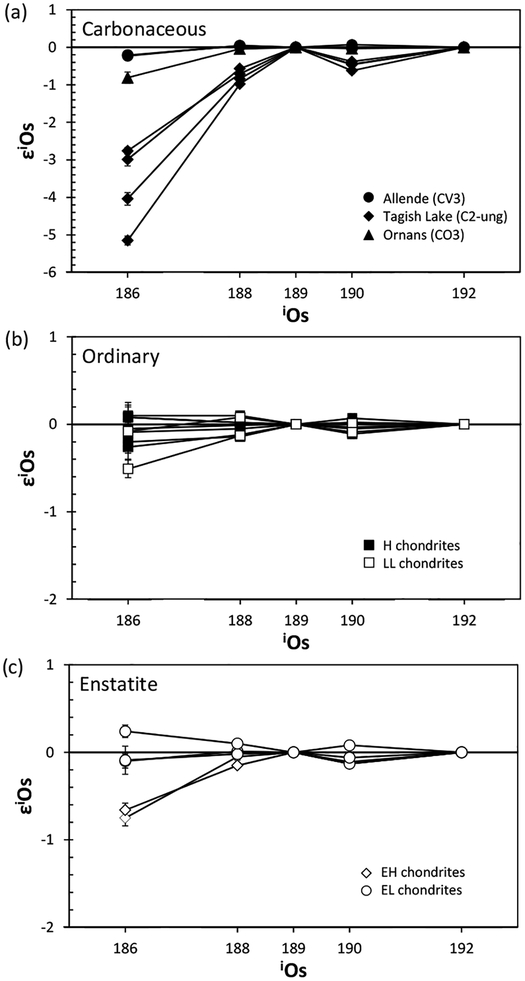
ε186Osi/189Os*	−0.73 to 0.49	−0.07 to 0.18	−0.39 to 0.33	0.03			2 ± 0.36
ε188Os/189Os	−0.17 to 0.10	0.00 to 0.13	−0.16 to 0.23	0.06			0 ± 0.07
ε190Os/189Os	−0.09 to 0.07	−0.03 to 0.04	−0.03 to 0.03	−0.07			0 ± 0.10
References	[8,9]	[8,9]	[8,9]	[10]			[9]
ε186Osi/188Os*					−0.06 to 0.79	−0.12	2 ± 0.25
ε188Os/188Os					−0.55 to 0.06	−0.17 to 0.03	0 ± 0.17
ε190Os/188Os					−0.03 to 0.31	−0.10 to 0.11	0 ± 0.13
References					[11]**	[11]**	[11]

References:

^[1]Burkhardt et al. (2011)

^[2]Chen et al. (2010)

^[3]Fischer-Gödde et al. (2013)

^[4]Fehr et al. (2005)

^[5]Fehr et al. (2004)

^[6]Kleine et al. (2004)

^[7]Qin et al. (2008)

^[8]Yokoyama et al. (2007)

^[9]Yokoyama et al. (2010)

^[10]van Acken (2011)

^[11]Walker (2012).

^*ε¹⁸⁶Osⁱ/^188,189Os are the part per 10⁴ deviation of the calculated initial ¹⁸⁶Os/^188,189Os of meteorites from the initial ratios of the solar system. Note that ε¹⁸⁶Osⁱ/^188,189Os of the terrestrial standard are not identical to zero because the ¹⁸⁶Os/^188,189Os of the standard used (UMd Os) are elevated relative to chondrites.

^**Os isotope data for iron meteorites and pallasites reported in Walker (2012) contain samples affected by long-term cosmic ray exposures.

Note that in the study of nucleosynthetic isotope anomalies in extraterrestrial materials, the magnitude of an isotopic anomaly is commonly expressed as ε or μ notation;

$$\mathrm{\epsilon }{}^i\text{M}=\left\{\frac{{\left({}^{i}M/{}^{j}M\right)}_{\text{sample}}}{{\left({}^{i}M/{}^{j}M\right)}_{\text{standard}}}-1\right\}\times {10}^4$$ (1)

$$\mathrm{\mu }{}^i\text{M}=\left\{\frac{{\left({}^{i}M/{}^{j}M\right)}_{\text{sample}}}{{\left({}^{i}M/{}^{j}M\right)}_{\text{standard}}}-1\right\}\times {10}^6$$ (2)

where ⁱM and ^jM are target and reference isotopes of an element M, respectively.

Isotope anomalies of siderophile elements in bulk meteorites

Molybdenum.

Molybdenum is a moderately siderophile element with a CI chondrite abundance of 1.02 ± 0.11 μg/g (1σ) (Lodders 2003). Most meteorites, excluding some achondrites, have Mo abundances that are substantially higher than that of CI chondrites. In addition, recent development of the negative-thermal ionization mass spectrometry (N-TIMS) technique, and refinement of multi-collector-inductively coupled plasma mass spectrometry (MC-ICP-MS) techniques have dramatically reduced the amount of Mo necessary for performing high-precision isotope analysis compared to earlier studies utilizing positive-thermal ionization mass spectrometry (P-TIMS) techniques, making this element highly useful for the study of nucleosynthetic isotopic anomalies in meteorites.

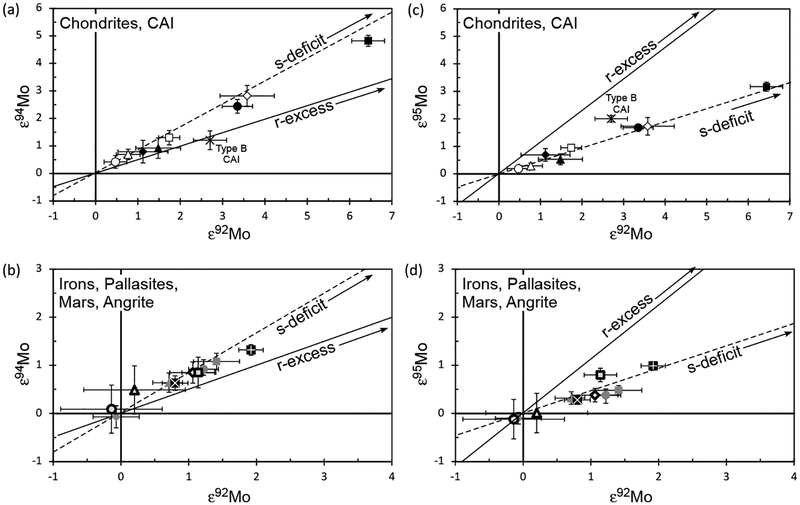
Molybdenum has seven stable isotopes ⁹²Mo, ⁹⁴Mo, ⁹⁵Mo, ⁹⁶Mo, ⁹⁷Mo, ⁹⁸Mo, and ¹⁰⁰Mo, with averaged terrestrial abundances of 14.8%, 9.23%, 15.9%, 16.7%, 9.56%, 24.2%, and 9.67%, respectively (Böhlke et al. 2005). Molybdenum isotopes are synthesized via stellar nucleosyntheses of the s-process (trace ⁹⁴Mo, ⁹⁵Mo, ⁹⁶Mo, ⁹⁷Mo, ⁹⁸Mo), the r-process (⁹⁵Mo, ⁹⁷Mo, ⁹⁸Mo, ¹⁰⁰Mo) and the p-process (⁹²Mo, ⁹⁴Mo). In addition, the p-process nuclide ⁹⁷Tc decays by electron capture to ⁹⁷Mo, with a half-life of 2.6 × 10⁶ yr. Because four out of seven Mo isotopes are produced almost entirely by a single nucleosynthetic process (^92,94Mo: p-process, ⁹⁶Mo: s-process, ¹⁰⁰Mo: r-process), the excess or deficit of a specific nucleosynthetic component, relative to the terrestrial component, makes for a distinctive Mo isotopic composition which is useful for diagnosing the origin of Mo isotope anomalies in meteorites.

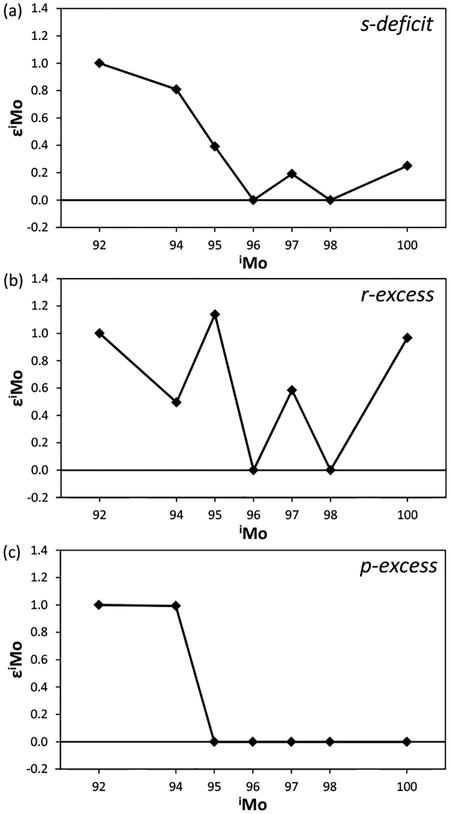
The pattern of εMo values for cases representing an excess or deficit of a pure nucleosynthetic component relative, to the terrestrial component, is shown in Figure 11. Note that ε⁹⁶Mo and ε⁹⁸Mo values are defined as zero because, for this diagram, the data acquired by mass spectrometry techniques are corrected for mass-dependent fractionation during isotopic measurement using ⁹⁸Mo/⁹⁶Mo = 1.453171 (Lu and Masuda 1994). The excess of a pure p-process component affects only ε⁹²Mo and ε⁹⁴Mo, while the deficit of a pure s-process component results in positive εMo values, excluding ε⁹⁶Mo and ε⁹⁸Mo, generating a W-shaped pattern (Fig. 11). By contrast, the excess of a pure r-process component produces a pattern akin to the case of s-process deficit, although a characteristic kink is observed in ε⁹⁴Mo. From the Mo isotopic patterns found in meteorites, therefore, it is theoretically possible to resolve the proportions of individual nucleosynthetic components within a sample.

Figure 11.

Molybdenum isotope patterns representing (a) s-deficit, (b) r-excess, and (c) p-excess relative to the terrestrial component. The model patterns were calculated by subtracting an s-process endmember component (Arlandini et al. 1999) from the solar system composition and scaled to a mixing ratio of (p + r)/s yielding ε⁹²Mo = 1.

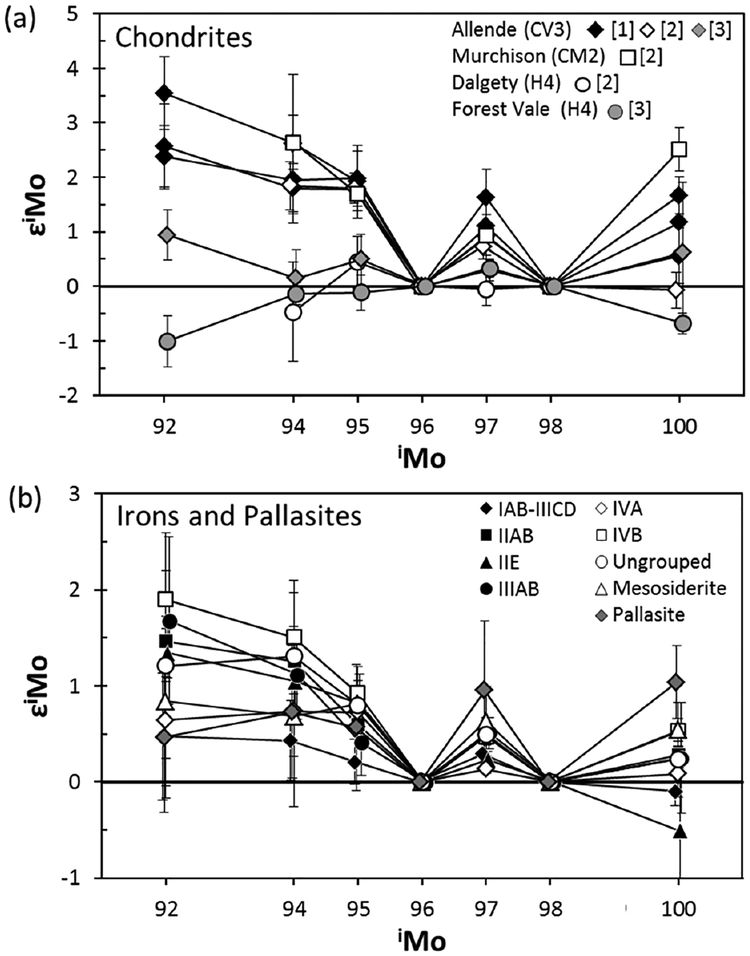
Review of three early studies of Mo isotope anomalies in meteorites (Dauphas et al. 2002a; Yin et al. 2002; Becker and Walker 2003a) is useful for highlighting the issues that must be considered when examining meteorites for nucleosynthetic isotope anomalies. Each of these studies reached different conclusions regarding the isotopic composition of Mo in meteorites. Yin et al. (2002) used N-TIMS to determine the Mo isotope compositions (excluding ⁹²Mo) in bulk aliquots of two carbonaceous chondrites, Murchison (CM2) and Allende (CV3). Dauphas et al. (2002a) utilized MC-ICP-MS for determining the Mo isotope composition of Allende. Both studies obtained W-shaped isotopic patterns (Fig. 12a) which resemble the case for s-process deficit (Fig. 11). Notably, the patterns they reported for Allende generally match the model pattern for p- and r-process excesses. By contrast, Becker and Walker (2003a) measured Mo isotope compositions in Allende and the H4 ordinary chondrite Forest Vail using N-TIMS, and found no resolvable Mo isotope anomalies.

Figure 12.

(a) Molybdenum isotope patterns for bulk aliquots of chondrites. Data sources: [1] Dauphas et al. (2002a), [2] Yin et al. (2002), [3] Becker and Walker (2003a). For [1] and [2], error bars are uncertainties of individual measurements estimated by 2 SE (standard error) of multiple lines of data acquisition in a single isotopic measurement. For [3], error bars are 2 SE of multiple data obtained by different isotopic measurements. (b) Mo isotope anomalies for iron meteorites (Dauphas et al. 2002a). Error bars are 2 SE of multiple isotopic measurements.

The inconsistencies between these studies were also evident for iron meteorites. Yin et al. (2002) analyzed five iron meteorites from four groups (IAB, IIAB, IIIAB, and IVB), and observed normal terrestrial Mo isotopic compositions for each. Similarly, Becker and Walker (2003a) observed no Mo isotope anomalies in two IIAB irons. In contrast to these two studies, Dauphas et al. (2002a) measured Mo isotopic compositions in fourteen iron meteorites from various groups (IAB-IIICD, IIAB, IIE, IIIAB, IVA, IVB, and ungrouped), as well as one mesosiderite and two pallasites, and detected anomalies in all of these meteorites. The anomalous patterns were similar to, but of lesser magnitude than observed in Allende (Fig. 12b).

As with the study of isotopic anomalies of any element in bulk planetary materials, at least three fundamental questions regarding the apparent Mo isotope anomalies must be addressed. First, are the anomalies reflective of the sample processed, or the result of an analytical artifact? For example, mass independent fractionation during TIMS/ICP-MS measurements has been well documented, as described below. Numerous factors can cause anomalous fractionation, which is a major concern for the determination of precise isotope ratios. For TIMS analysis, temperature gradients across the ionizing filament can lead to the generation of multiple sample domains on the filament that fractionate at different rates, resulting in the mixing of isotopically distinct reservoirs in the detectors. Such an isotope mixing from vigorously and weakly fractionated reservoirs produces isotopic compositions that deviate from the exponential law curve that is commonly used for correcting mass fractionation (Upadhyay et al. 2008). In the case of MC-ICP-MS analysis, the cross section of ion beams generated by plasma ionization is so broad, relative to thermal ionization, that the beams may be partially clipped in the flight tube and cause mass independent fractionation (Albarède et al. 2004). Furthermore, an odd–even isotope separation, dependent on the shape of the sampler and skimmer cones, was reported for precise W isotope analysis using MC-ICP-MS (Shirai and Humayun 2011). Most of these problems are not reproducible and are difficult to evaluate with the mass spectrometers used in the studies noted above. Analytical artifacts can also result from isobaric interferences from other elemental or molecular species that are ionized along with the element of interest, usually as a result of inadequate chemical purification.

Second, if the measurements are accurate and precise to the level of precision reported, do anomalous isotopic compositions reflect the incomplete digestion of the sample, with complementary anomalies residing in materials that remained un-accessed by the dissolution method? For instance, presolar SiC is very acid-resistant, so incomplete dissolution of s-process-enriched mainstream presolar SiC grains would result in an apparent Mo isotope pattern for a bulk meteorite with an s-process deficit (W-shaped), assuming the true bulk sample had a terrestrial Mo isotopic composition (no anomalies). This is a very real possibility for some elements in some meteorites that contain relatively abundant presolar SiC, because dissolution of SiC using normal acids, especially in non-pressurized digestion vessels, is quite limited. In the case of Murchison which contains 9 ppm of presolar SiC (Huss et al. 2003), the incomplete digestion of SiC could result in ε⁹⁴Mo and ε¹⁰⁰Mo values of ~ + 0.45, if it is assumed that bulk Murchison has no Mo isotopic anomalies. By contrast, Allende contains very little SiC (0.01 ppm) due to the destruction of presolar grains by thermal metamorphism on the parent body (Huss et al. 2003). Consequently, anomalies of the magnitude reported by Yin et al. (2002) and Dauphas et al. (2002a) for this meteorite are unlikely to reflect incomplete sample dissolution. It should also be noted that iron meteorites solidified from liquid metal at conditions under which presolar grains cannot survive. Hence, anomalies present in iron meteorites, as well as the metal portions of stony irons, cannot be explained as a result of incomplete dissolution. As a corollary, because individual members of a so called “magmatic” iron meteorite group (e.g., IIAB, IID, IIIAB, IVA, and IVB) formed as part of a crystal-liquid fractionation sequence of genetically identical materials (e.g., Pernicka and Wasson 1987), irons of a given group should be expected to be characterized by identical anomalies.

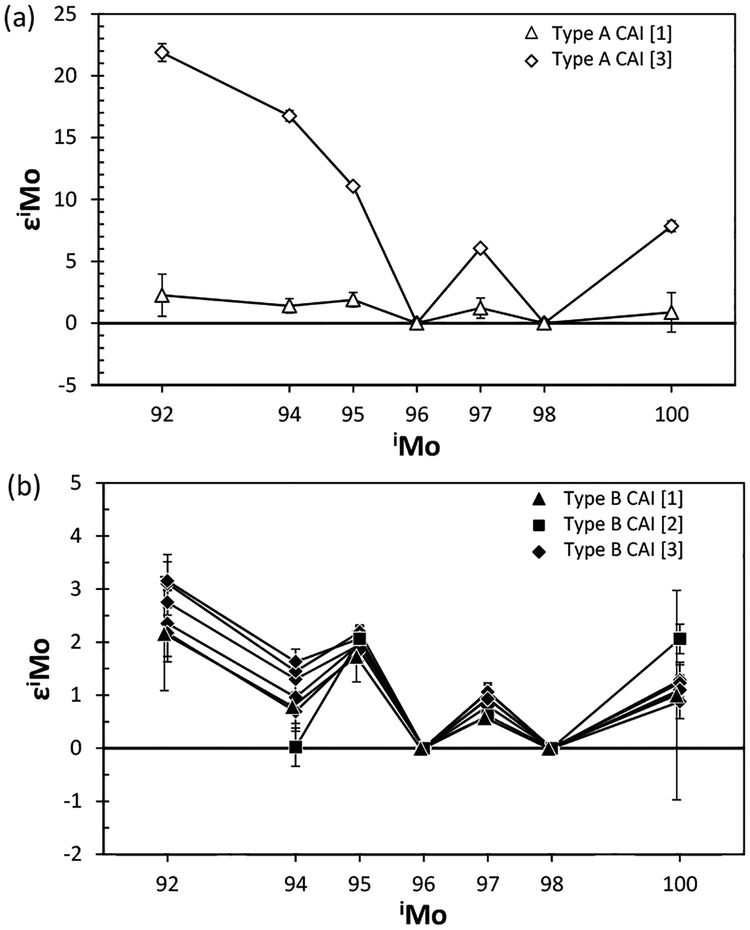
A third question relates to whether or not a portion of a meteorite characterized by nucleosynthetic anomalies is representative of the bulk meteorite. For example, lithological heterogeneity among pieces of a single meteorite can lead to varying conclusions regarding the nature and magnitude of isotope anomalies present in the meteorite. This is because some chondritic components, such as the irregularly-distributed calcium-aluminum rich inclusions (CAIs) can contain both high abundances of an element such as Mo, as well diverse isotopic compositions (e.g., Yin et al. 2002). Thus, the analysis of different portions of a chondrite characterized by differing proportions of CAIs, such as Allende, may yield inconsistent results, especially when processing the typically ≤1 g aliquots used for such studies. Nevertheless, in the case of Allende, most CAIs present in this meteorite are characterized by Mo isotope anomalies with r-process excesses (see later section for CAI), making it difficult to produce a W-shaped pattern of s-process deficits without a kink in ε⁹⁴Mo.

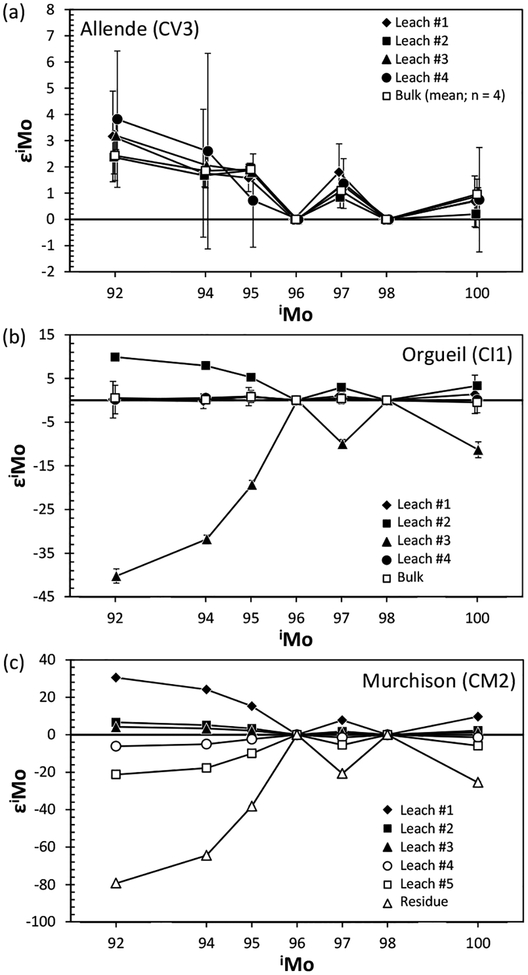
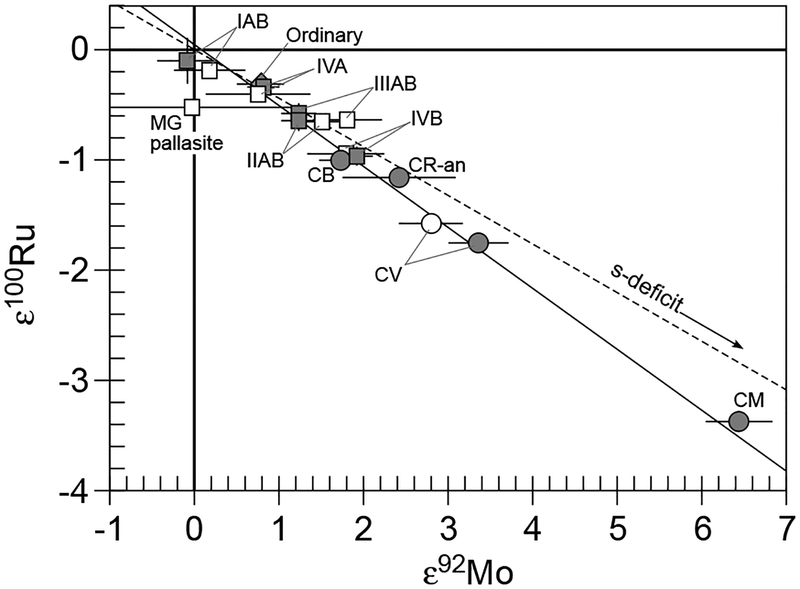
More recently, a comprehensive analysis of Mo isotope compositions for a wide range of meteorite samples was made using a newer generation MC-ICP-MS with analytical precisions several times better than early studies (Burkhardt et al. 2011). To overcome the problem of incomplete digestion of refractory presolar grains, the authors conducted complete melting of carbonaceous chondrites using CO₂ laser fusion in ultra-pure graphite capsules under oxidizing (atmospheric) or reducing (7% H₂–93% Ar) conditions prior to sample digestion with acids (Pack et al. 2010). They discovered that the Mo isotope composition of a CO₂-fused Murchison sample was indistinguishable from those of acid-digested Murchison, suggesting that incomplete digestion of presolar grains in chondrites via conventional acid digestion with HF–HNO₃–HClO₄ would not have a measurable effect on the Mo isotope composition.

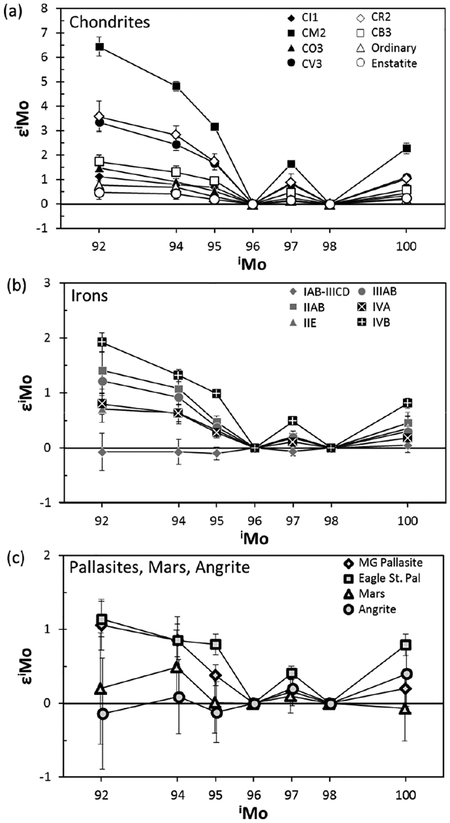
With the CO₂ fusion method, Burkhardt et al. (2011) analyzed Mo isotope compositions for bulk aliquots of five carbonaceous chondrites (CI, CM2, CR2, CO3, CV3) and one enstatite chondrite (EH4). In addition, bulk samples of two ordinary (H3, H6) and two enstatite chondrites (EH4, EL6), as well as metal fractions from two carbonaceous (CR-an, CB) and two ordinary chondrites (L6, LL6) were examined using conventional acid digestion. As shown in Figure 13, all chondrites display positive εMo values with W-shaped patterns indicative of s-process Mo deficits. This observation is even more pronounced when the data are plotted in εⁱMo–ε⁹²Mo space (Fig. 14), where mixing lines between terrestrial Mo and either a pure s-process or a pure r-process component are clearly discriminated from each other. Excluding one CM chondrite, the chondrite data follow the theoretical s-process mixing line, of which one end-member component is defined by data for SiC grains measured by RIMS (Nicolussi et al. 1998a). The magnitude of Mo isotope anomalies is in the order ofindicating no meaningful correlation between Mo isotope anomaly and lithological and chemical properties. More importantly, enstatite chondrites have Mo isotope compositions that are marginally resolvable from the terrestrial composition. This is comparable to recent high-precision observations for a variety of other elements in enstatite chondrites that have stable isotope compositions similar or identical to those of terrestrial (e.g., O, N, Cr, Ru, Os: Javoy et al. 2010; Herwartz et al. 2014).

Figure 13.

Molybdenum isotope patterns for (a) bulk chondrites, (b) iron meteorites, and (c) pallasites, angrite and Martian meteorite. Data are from Burkhardt et al. (2011). Error bars are 2 SE of multiple data obtained by different isotopic measurements excluding angrite and Martian meteorite for which 2 SD (standard deviation) from repeated analyses of a terrestrial standard is applied.

Figure 14.

Plots of Mo isotope anomalies in εⁱMo–ε⁹²Mo space for meteorites and CAI. Data are from Burkhardt et al. (2011). Symbols and errors are the same as Figure 13.

The authors also analyzed Mo isotope compositions in differentiated meteorites, including iron meteorites from various groups (IAB-IIICD, IC, IID, IIE, IIIAB, IIIE, IIIF, IVAB, ungrouped), two pallasites, two Martian meteorites, and one angrite. Of these samples, all magmatic irons (IIAB, IID, IIIAB, IVA, IVB), IIE irons, and pallasites exhibit positive Mo isotope anomalies with W-shaped patterns, without an ε⁹⁴Mo kink, whereas the rest do not have any resolvable Mo isotope anomalies. These results are in general agreement with the result of Dauphas et al. (2002a). No meteorites studied have Mo isotope anomalies with negative εMo values. This implies that the Earth, Mars, and that the parent bodies of angrite and non-magmatic IAB-IIICD irons, accreted from precursor material with the most s-process enriched Mo of any cosmochemical materials yet studied, presumably in the inner region of the early Solar System, where the building blocks of meteorite parent bodies formed.

The most likely cause of the discrepancies between the early studies and Burkhardt et al. (2011) is simply the issue of analytical precision. Becker and Walker (2003a) and Yin et al. (2002) did not detect the smaller anomalies because of large analytical uncertainties.

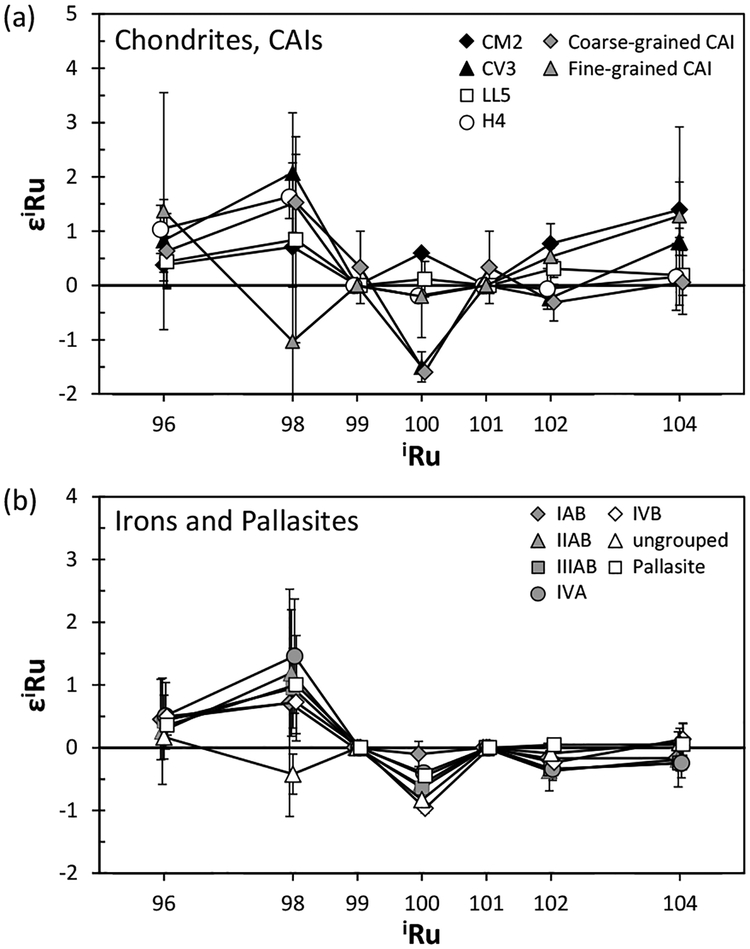
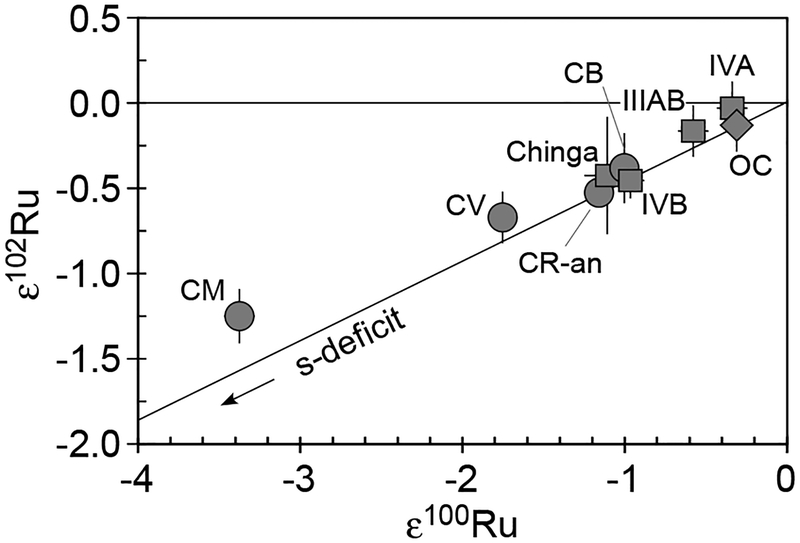
Ruthenium.

Ruthenium is a highly siderophile element with a CI chondrite abundance of 0.692 ± 0.044 μg/g (Lodders 2003). It has seven stable isotopes ⁹⁶Ru, ⁹⁸Ru, ⁹⁹Ru, ¹⁰⁰Ru, ¹⁰¹Ru, ¹⁰²Ru, and ¹⁰⁴Ru, with averaged terrestrial abundances of 5.54%, 1.87%, 12.8%, 12.6%, 17.1%, 31.6%, and 18.6%, respectively (Böhlke et al. 2005). Ruthenium isotopes are synthesized via stellar nucleosyntheses of the p-process (⁹⁶Ru, ⁹⁸Ru), the s-process (¹⁰⁰Ru), and the r-process (¹⁰⁴Ru). Three isotopes are synthesized both by the s- and r-processes (⁹⁹Ru, ¹⁰¹Ru, ¹⁰²Ru). In addition, the short-lived ⁹⁸Tc and ⁹⁹Tc decay to ⁹⁸Ru and ⁹⁹Ru; ⁹⁸Tc is synthesized by the p-process, while ⁹⁹Tc lies along the s-process path (Fig. 4). The half-life of ⁹⁸Tc is poorly constrained, with estimates ranging from 4.2 to 10 Myr (Kobayashi et al. 1993; Parrington et al. 1996). By contrast, the half-life of ⁹⁹Tc is only 213 kyr (Parrington et al. 1996). High precision Ru isotope analyses have been conducted by both N-TIMS and MC-ICP-MS.

Precise Ru isotopic data with MC-ICP-MS for five IIAB and two IIIAB iron meteorites, as well as one carbonaceous chondrite (CV3) and one ordinary chondrite (H5) indicated that the ⁹⁸Ru/¹⁰¹Ru and ⁹⁹Ru/¹⁰¹Ru ratios in these meteorites overlapped with the terrestrial values within the ± 0.8 and ± 0.3ε levels of precision reported (2σ_M), respectively (Becker and Walker 2003b). This implies that these meteorites present no sign of early Tc/Ru fractionation as detectable in Ru isotope shifts, nor do they possess nucleosynthetic Ru isotope anomalies above the stated levels of uncertainty.

Chen et al. (2010) subsequently conducted a comprehensive study of Ru isotopes in two carbonaceous chondrites (CM2, CV3), four ordinary chondrites (LL5, three H4), thirteen iron meteorites from varying groups (IAB, IIAB, IIIAB, IVA, IVB, ungrouped), and three pallasites. This study utilized N-TIMS and reported external precision for ⁹⁸Ru/¹⁰¹Ru and ¹⁰⁰Ru/¹⁰¹Ru at the ± 2.0 and ± 0.3ε levels, respectively (2σ). The authors found no Ru isotopic effects in the ordinary chondrites and IAB iron meteorites, whereas significant deficits were observed in ¹⁰⁰Ru/¹⁰¹Ru ratios for a bulk aliquot of Allende (CV3) (up to – 1.7ε), and the rest of the iron meteorites and pallasites (up to – 1.1ε) (Fig. 15). Incomplete sample digestion would not account for the observed anomalies because all the isotopically anomalous samples contain minuscule or no presolar grains. Rather, the results suggest a widespread and large-scale Ru isotopic heterogeneity in the early Solar System, resulting in a deficit in s-process nuclides or enhancements in both p- and r-process nuclides in the early solar nebula. Chen et al. (2010) argued that the inconsistency between their study and Becker and Walker (2003b) arose from different approaches for correcting mass-dependent fractionation; Chen et al. used ⁹⁹Ru/¹⁰¹Ru for normalization whereas Becker and Walker used ⁹⁶Ru/¹⁰¹Ru. They also presumed that the precision of the other Ru isotope ratios was inadequate to detect the expected isotope shifts in ^{96,98,102,104}Ru/¹⁰¹Ru ratios, owing to an s-process deficit, which were smaller than the change on ¹⁰⁰Ru/¹⁰¹Ru. This problem was resolved by recent high precision Ru isotope analyses with MC-ICP-MS for a series of chondrites and iron meteorites (Fischer-Gödde et al. 2012, 2013). When Ru isotope ratios were normalized with ⁹⁹Ru/¹⁰¹Ru for mass fractionation, the data displayed negative ε¹⁰⁰Ru values which clearly correlated with ε¹⁰²Ru values, consistent with s-process deficit (Fig. 16) (Fischer-Gödde et al. 2012, 2013).

Figure 15.

Ruthenium isotope compositions for chondrites, CAIs, and iron meteorites in εRu units. Data are from Chen et al. (2010). Error bars are 2SE of multiple data obtained by different isotopic measurements excluding fine-grained CAI for which internal precision of individual isotopic run is applied.

Figure 16.

Plot of Ru isotope anomalies for chondrites and iron meteorites in ε¹⁰²Mo–ε¹⁰⁰Ru space. Data are from Fischer-Gödde et al. (2013).

Tungsten.

Tungsten is a moderately siderophile element with a CI chondrite abundance of 0.089 ± 0.007 μg/g (Lodders 2003). It has five stable isotopes ¹⁸⁰W, ¹⁸²W, ¹⁸³W, ¹⁸⁴W, and ¹⁸⁶W with averaged terrestrial abundances of 0.12%, 26.5%, 14.3%, 30.6%, and 28.4%, respectively (Böhlke et al. 2005). One minor W isotope (¹⁸⁰W) is synthesized via the stellar nucleosynthesis of the p-process, and the rests are synthesized by the s- and r-processes (¹⁸²W, ¹⁸³W, ¹⁸⁴W, ¹⁸⁶W). In addition, the short-lived ¹⁸²Hf, which is a predominantly r-process isotope, decays to ¹⁸²W with a half-life of 8.9 Myr (Vockenhuber et al. 2004) making the ¹⁸²Hf–¹⁸²W system useful for chronological applications regarding processes associated with the formation and earliest evolution of planetary bodies (e.g., Kleine et al. 2009). Compared to numerous studies of ¹⁸²Hf–¹⁸²W systematics, studies focused primarily on nucleosynthetic W isotope anomalies in meteorites are limited. There are at least two reasons for the scarcity. First, excluding very minor (¹⁸⁰W) and radiogenic (¹⁸²W) isotopes, there are only three W isotopes usable for the study of nucleosynthetic isotope anomalies. Second, exposure to galactic cosmic radiation (GCR) can modify the W isotope compositions of extraterrestrial materials, especially for iron meteorites. Third, most W isotopes were synthesized by two processes (s and r) in nearly equal proportions, making it unlikely for nature to generate large isotopic variations, as observed in Mo isotopes. Consequently, many studies have reported ¹⁸³W/¹⁸⁴W (or ¹⁸⁴W/¹⁸³W) as simply an additional quality check for ¹⁸²W data.

Kleine et al. (2004) measured the ¹⁸³W/¹⁸⁴W ratios in a variety of chondrites as well as eucrites and Martian meteorites, and found no detectable isotope anomalies. Irisawa et al. (2009) measured W isotope ratios for a suite of carbonaceous and ordinary chondrites and found a small deficit in ¹⁸⁴W/¹⁸³W at a level of ~0.4ε for the Allende meteorite (CV3), but not for the other chondrites. These authors argued that the observed anomalies could not be due to the incomplete digestion of presolar SiC grains because the amount of surviving presolar SiC in Allende is significantly lower than for most other carbonaceous chondrites. Rather, they attributed the anomaly to differing proportions of isotopically anomalous CAIs in the samples studied. Further, Qin et al. (2008) reported deficits of ~0.1ε in ¹⁸⁴W/¹⁸³W ratios for IVB magmatic iron meteorites relative to the terrestrial standard and IIAB iron meteorites. These authors concluded that the observed stable W isotope heterogeneity reflected incomplete mixing of the products of s- and r-process components in the solar nebula.

Osmium.

Osmium is a highly siderophile element with a mean CI chondrite abundance of 0.486 μg/g (Lodders 2003). The search for nucleosynthetic isotope anomalies of Os in meteorites has been achieved almost exclusively using the N-TIMS technique. Osmium has seven stable isotopes ¹⁸⁴Os, ¹⁸⁶Os, ¹⁸⁷Os, ¹⁸⁸Os, ¹⁸⁹Os, ¹⁹⁰Os, and ¹⁹²Os, which are synthesized via stellar nucleosyntheses of the p-process (¹⁸⁴Os), s-process (¹⁸⁷Os), p- and s-processes (¹⁸⁶Os), and s-and r-processes (¹⁸⁸Os, ¹⁸⁹Os, ¹⁹⁰Os and ¹⁹²Os). In addition to these processes, ¹⁸⁶Os and ¹⁸⁷Os are produced by radioactive decay of ¹⁹⁰Pt (T_1/2 = 488 Gyr) and ¹⁸⁷Re (T_1/2 = 41.5 Gyr). Platinum-190 is a pure p-process isotope, while ¹⁸⁷Re is predominantly produced by the r-process. Because of the radiogenic isotopes, the terrestrial Os isotope composition cannot be uniquely determined. One of the more widely distributed Os isotope reference materials (UMd Os) has isotopic abundances of ¹⁸⁴Os = 0.017%, ¹⁸⁶Os = 1.59%, ¹⁸⁷Os = 1.51%, ¹⁸⁸Os = 13.30%, ¹⁸⁹Os = 16.22%, ¹⁹⁰Os = 26.38%, and ¹⁹²Os = 40.99%, although this particular standard has slightly sub-chondritic ¹⁸⁷Os/¹⁸⁸Os and elevated ¹⁸⁶Os/¹⁸⁸Os (Yokoyama et al. 2010).

Of the seven isotopes, two (¹⁸⁹Os, ¹⁹²Os) have large (> 90%) contributions from the r-process. In order to resolve possible nucleosynthetic isotope anomalies, ¹⁸⁹Os has been used as the denominator of isotopic pairs, rather than the commonly used ¹⁸⁸Os. Further, isotopic fractionation during mass spectrometry is best corrected using a fixed ¹⁹²Os/¹⁸⁹Os (= 2.527411: Yokoyama et al. 2007). The radiogenic isotope ¹⁸⁷Os is not utilized in the study of nucleosynthetic isotope anomalies because of the difficulty in determining the contribution from ¹⁸⁷Re decay over 4.567 Ga in meteorites with sufficient accuracy. However, ¹⁸⁶Os can be regarded as a stable isotope after the typically minor correction for ¹⁹⁰Pt decay using the Pt/Os ratio in most cosmochemical samples. This is possible because of the long half-life and minor abundance (0.014%) of ¹⁹⁰Pt relative to ¹⁸⁷Re. Unlike Mo and Ru isotopes, the contribution of p-process nuclides to the total Os is minuscule (~ 0.02%), and Os is composed almost entirely of s- and r-process nuclides. Therefore, Os isotope anomalies with s-process deficits almost completely match the isotopic pattern given by r-process excesses.

The first high precision stable Os isotope analysis for bulk meteorites was reported by Brandon et al. (2005). They determined Os isotope compositions in bulk aliquots of three carbonaceous chondrites (C2-ung, CV3, CO3), seven ordinary chondrites (H3.4, two H4, two H5, LL3.4, LL3.6), and three enstatite chondrites (EH4 and two EL6) by applying the Carius tube digestion using a mixture of HNO₃ and HCl (Shirey and Walker 1995). One problem evaluating the magnitude of Os isotope anomalies in meteorites is the selection of a standard reference material, because terrestrial samples are known to have variable ¹⁸⁶Os/¹⁸⁹Os, due to the long-term evolution of ¹⁸⁶Os with supra- or sub-chondritic Pt/Os ratios. Thus, reference standards made from these materials do not necessarily represent the bulk Earth composition. To resolve this issue, Brandon et al. (2005) used the mean Os isotope composition of five H-group ordinary chondrites measured in their study as an averaged Solar System component, which exhibited uniform Os isotope ratios identical to the terrestrial values, but have an ¹⁸⁶Os/¹⁸⁹Os different from that of the standard reference material they used.

Figure 17 shows Os isotope compositions in εOs units normalized to the mean of H chondrites. The ε¹⁸⁶Osⁱ indicates the initial ε¹⁸⁶Os value corrected for ¹⁹⁰Pt decay over 4.56 Ga using the measured Pt/Os ratio. As presented in this Figure, most of the ordinary and enstatite chondrites show no Os isotope anomalies, except for slightly negative ε¹⁸⁶Osⁱ values of Parnellee (LL 3.6) and Indarch (EH4). By contrast, significant, large negative Os isotope anomalies are evident for ε¹⁸⁶Osⁱ, ε ¹⁸⁸Os, and ε¹⁹⁰Os values in the carbonaceous chondrite Tagish Lake (C2-ung). The εOs values for the rest of carbonaceous chondrites were not resolvable from the bulk Solar System, excluding a small negative ε¹⁸⁶Osⁱ value for Ornans (CO3). The magnitude of negative Os isotope anomalies in Tagish Lake is in the order of ε¹⁸⁶Osⁱ > ε¹⁸⁸Os > ε¹⁹⁰Os, suggesting that the anomalies are deficits of s-process origin. An important observation is that replicate measurements of four different Tagish Lake dissolutions resulted in varying εOs values, as clearly shown in ε¹⁸⁶Osⁱ. Brandon et al. (2005) interpreted the observed isotope anomalies to be a result of incomplete digestion of isotopically anomalous acid resistant carriers in chondrites, most likely s-process enriched presolar SiC grains. Such grains are abundant in Tagish Lake (~5 to 8 ppm), and are also present in less metamorphosed carbonaceous and ordinary chondrites (petrologic grade less than 3.8), as well as in enstatite chondrites of type 3–4 (Russell et al. 1997; Huss et al. 2003). The Tagish Lake data suggest that sample digestion with HNO₃ and HCl in Carius tubes dissolve varying proportions of SiC, resulting in non-reproducible εOs values. As mentioned above, conventional acid digestion with HF-HNO₃-HClO₄ would not have a measurable effect on the Mo isotope composition of SiC bearing chondrites. This is clearly not the case of Os with Carius tube digestion. Therefore, the presence or absence of planetary scale Os isotope heterogeneity remained unclear from this study, and indicated a need for Os isotopic analyses utilizing total sample digestion.

Figure 17.

Osmium isotope compositions in (a) carbonaceous, (b) ordinary, and (c) enstatite chondrites. Data are from Brandon et al. (2005). Error bars are 2 SE of individual measurements.

The problem of incomplete sample digestion was resolved by Yokoyama et al. (2007, 2010) who applied an alkaline fusion technique that can completely dissolve all chondrite constituents, including presolar SiC. In two studies, the authors analyzed Os isotope compositions in eight carbonaceous chondrites (CI1, C2-ung, two CR2, CM2, two CV3, CK4), three ordinary chondrites (H3.8, two H5), and five enstatite chondrites (EH4, four EL6). Although most of the carbonaceous chondrites analyzed contain abundant presolar SiC grains, they obtained uniform εOs values, which were not resolvable from the terrestrial values, excluding ε¹⁸⁶Osⁱ across all chondrite classes (Fig. 18). In addition, negative εOs values were observed when SiC bearing carbonaceous chondrites (C2-ung, CM2, CR2) were digested by the Carius tube method (Yokoyama et al. 2007). This implies that Os isotope anomalies in bulk chondrites observed in Brandon et al. (2005) were caused by incomplete sample digestion, as postulated by that study, and that all chondrites and the silicate portion of the Earth most likely possess a common Os isotope composition.

Figure 18.

μ¹⁸⁸Os values for CAIs, chondrites, iron meteorites, and pallasites. Error bars are 2 SE for samples with multiple analyses or the internal precision of individual isotopic run for samples with single measurement. Data sources: Yokoyama et al. (2007, 2010, 2011) and Walker (2012).

The homogenous Os isotope distribution was further corroborated by two subsequent studies. Van Acken et al. (2011) conducted precise Os isotope analyses for a variety of enstatite and Rumuruti chondrites, as well as one differentiated meteorite (aubrite). Because these samples were decomposed by the Carius tube method, some low petrologic grade enstatite and Rumuruti chondrites exhibited small but resolvable Os isotope anomalies due to incomplete sample dissolution, whereas the rest of the samples, including high grade chondrites, show values indistinguishable from the Solar System average.

Extending the search for nucleosynthetic Os anomalies to other planetary materials, Walker (2012) analyzed Os isotope compositions in iron meteorites from groups IAB, IIAB, IIIAB, IVA, and IVB, as well as the main group pallasites. A large proportion of these meteorites exhibit Os isotope anomalies in ε¹⁸⁶Osⁱ, ε¹⁸⁹Os, and ε¹⁹⁰Os values (note that the author used ¹⁸⁸Os as the denominator of isotope ratios). However, the observed anomalies differ from nucleosynthetic Os isotope anomalies in chondrite constituents (see below), implying that the Os isotope anomalies in iron meteorites most likely reflect long-term exposure of the meteorites to cosmic rays, rather than nucleosynthetic effects. In fact, the ε¹⁹⁰Os versus ε¹⁸⁶Osⁱ and ε¹⁸⁹Os trends defined by the iron meteorites and pallasites have end-member compositions defined by samples with limited or no cosmic ray exposure, of which the εOs values are normal and unresolved from the chondritic composition.

Overall, the uniform Os isotope composition in bulk chondrites, as well as in differentiated meteorites, strongly suggests that dust grains with disparate isotopic Os isotopic compositions were thoroughly mixed within the solar nebula at the time of the initiation of planetesimal accretion. This conclusion contrasts with evidence for heterogeneous isotope compositions among early Solar System materials for numerous other elements (e.g., Ti, Cr, Ni, Mo, Ru, Ba, Nd, and Sm: Dauphas et al. 2002a; Andreasen and Sharma 2006; Carlson et al. 2007; Trinquier et al. 2007; Regelous et al. 2008; Trinquier et al. 2009; Chen et al. 2010; Qin et al. 2010; Burkhardt et al. 2011). The contrast must reflect physical and chemical processes in the early Solar System that acted differently on individual elements. This issue will be discussed later in detail.

Platinum.

Platinum is a HSE with a CI chondrite abundance of 1.004 μg/g (Lodders 2003). It has five stable isotopes ¹⁹²Pt, ¹⁹⁴Pt, ¹⁹⁵Pt, ¹⁹⁶Pt, and ¹⁹⁸Pt with averaged terrestrial abundances of 0.78%, 33.0%, 33.8%, 25.2%, and 7.16%, respectively (Böhlke et al. 2005). In addition, one minor radioactive isotope ¹⁹⁰Pt (T_1/2 = 488 Gyr) exists with a terrestrial abundance of 0.014%. Platinum isotopes are synthesized via stellar nucleosyntheses by the p-process (¹⁹⁰Pt), the s-process (¹⁹²Pt), and the r-process (¹⁹⁸Pt). Three isotopes are synthesized by both the s- and r-processes (¹⁹⁴Pt, ¹⁹⁵Pt, ¹⁹⁶Pt). Platinum is a typical r-process element because four major isotopes (¹⁹⁴Pt–¹⁹⁸Pt) are nearly all (> 90%) synthesized by the r-process (Arlandini et al. 1999).

High precision Pt isotope analyses reported for meteorites are rare. The majority of the data are for iron meteorites examined with MC-ICP-MS (Kruijer et al. 2013; Wittig et al. 2013). These studies have utilized Pt isotopes as a tracer for quantitatively evaluating the effect of cosmic ray exposure in order to correct ¹⁸²W/¹⁸⁴W ratios for exposure. These studies discovered that nearly all samples from IID, IVA, and IVB iron meteorites exhibit significant isotope anomalies in ¹⁹²Pt/¹⁹⁵Pt and ¹⁹⁶Pt/¹⁹⁵Pt ratios with anomalies as great as + 58.6ε and + 0.88ε, relative to those of a terrestrial standard, respectively. They interpreted, however, that the observed anomalies were not nucleosynthetic in origin but represent the effect of neutron capture on Pt isotopes via cosmic ray exposure. This is because: 1) Pt isotope compositions of different irons from a same group varied randomly as opposed to the observation of Mo and Ru isotopes, and, 2) no correlation was observed in a ε¹⁹²Pt–ε¹⁹⁶Pt diagram. These authors concluded that no nucleosynthetic Pt isotope anomalies were resolvable at the current level of analytical precision.

Isotope anomalies of chalcophile elements in bulk meteorites

In the following, we review evidence for nucleosynthetic isotope anomalies in meteorites for three chalcophile elements, Cd, Sn, and Te. Cadmium, Sn and Te are classified as moderately volatile elements with 50% condensation temperatures of 652 K, 704 K, and 709 K, respectively (Lodders 2003). Most of the recent investigations regarding isotope anomalies in meteorites focused on refractory elements, including siderophile elements as reviewed above, whereas isotopic data for moderately volatile elements are limited. The abundances of Cd, Sn, and Te in CI chondrite are the highest relative to the other types of chondrites. Moderately volatile elements, including Cd, Sn, and Te, occur in much lower concentrations in differentiated meteorites, excluding some iron meteorites, with typical levels of 0.1 × CI or less (e.g., Laul et al. 1972). Low abundances in most achondrites make these elements problematic for high-precision isotopic analysis. The depletion of moderately volatile elements in chondrites and achondrites, relative to CI chondrites, has generally been interpreted to reflect incomplete stepwise accretion of nebular material (Humayun and Clayton 1995; Albarède 2009), rather than as a result of loss by outgassing from dust grains/chondrules/planetesimals.

Cadmium.

The CI chondrite abundance of Cd is 0.675 ± 0.006 μg/g (1σ) (Lodders 2003). Cadmium has eight stable isotopes, ¹⁰⁶Cd, ¹⁰⁸Cd, ¹¹⁰Cd, ¹¹¹Cd, ¹¹²Cd, ¹¹³Cd, ¹¹⁴Cd, and ¹¹⁶Cd with averaged terrestrial abundances of 1.25%, 0.89%, 12.5%, 12.8%, 24.1%, 12.2%, 28.7%, and 7.49%, respectively (Böhlke et al. 2005). Cadmium isotopes are synthesized by the stellar nucleosynthesis of the p-process (¹⁰⁶Cd, ¹⁰⁸Cd), the s-process (¹¹⁰Cd), and the r-process (¹¹⁶Cd). Four Cd isotopes are synthesized both by the s- and r-processes (¹¹¹Cd, ¹¹²Cd, ¹¹³Cd, ¹¹⁴Cd). Because Cd is one of the most volatile elements among siderophile and chalcophile elements, Cd isotopes been primarily used for tracking processes associated with vaporization in geochemistry and cosmochemistry (e.g., Wombacher et al. 2003, 2004; Ripperger and Rehkämper 2007). These studies utilized MC-ICP-MS for high precision Cd isotope analysis.

Wombacher et al. (2008) determined precise Cd isotope compositions for a comprehensive suite of carbonaceous, ordinary, enstatite, and Rumuruti chondrites, as well as achondrites and lunar samples (soils, breccias, pristine anorthosite). However, none of the samples showed evidence of nucleosynthetic anomalies for the s- and r-process nuclides ¹¹¹Cd, ¹¹²Cd, ¹¹³Cd, and ¹¹⁴Cd, nor for the pure s-process isotope ¹¹⁰Cd. Although data for two minor p-process nuclides are not available (¹⁰⁶Cd, ¹⁰⁸Cd), the result is consistent with another moderately volatile chalcophile element, Te (see below).

Tin.

The CI chondrite abundance of Sn is 1.68 ± 0.04 μg/g (1σ) (Lodders 2003). Tin has ten stable isotopes, ¹¹²Sn, ¹¹⁴Sn, ¹¹⁵Sn, ¹¹⁶Sn, ¹¹⁷Sn, ¹¹⁸Sn, ¹¹⁹Sn, ¹²⁰Sn, ¹²²Sn, and ¹²⁴Sn with averaged terrestrial abundances of 0.97%, 0.66%, 0.34%, 14.5%, 7.68%, 24.2%, 8.59%, 32.6%, 4.63%, and 5.79%, respectively (Böhlke et al. 2005). This is the largest number of stable isotopes among all elements of the periodic table. Six Sn isotopes are synthesized via single stellar nucleosyntheses; the p-process (¹¹²Sn, ¹¹⁴Sn, ¹¹⁵Sn), the s-process (¹¹⁶Sn), and the r-process (¹²²Sn, ¹²⁴Sn). The rest are synthesized both by the s- and r-processes (¹¹⁷Sn, ¹¹⁸Sn, ¹¹⁹Sn, ¹²⁰Sn). The large number of isotopes produced by various nucleosynthetic processes make Sn a promising element for the study of nucleosynthetic isotope anomalies in meteorites. However, high precision Sn isotope data for meteorites are not currently available. An early study of Sn isotopes using TIMS discovered no significant isotope anomalies in four iron meteorites or in the metal phase of one mesosiderite (De Laeter and Jeffery 1965). Recently, high precision Sn isotope analyses have been made mainly by MC-ICP-MS (e.g., Lee and Halliday 1995; Moynier et al. 2009; Haustein et al. 2010; Yamazaki et al. 2013). However, sample digestion remains problematic for the analysis of Sn isotopes in meteorites. First, Sn is readily oxidized and precipitates in concentrated nitric acid as meta stannic acid. Second, when Sn is treated with hydrochloric acid, stannic chloride (SnCl₄) forms which vaporizes at 114° C (Yamazaki et al. 2013). One possible option for complete sample digestion and subsequent recovery of Sn is the alkali fusion technique, however, application of this method will require the development of new techniques for isolating Sn from the resulting sample solution containing significant amounts of alkali elements.

Tellurium.

The CI chondrite abundance of Te is 2.33 ± 0.18 μg/g (1σ) (Lodders 2003). Tellurium has eight stable isotopes, ¹²⁰Te, ¹²²Te, ¹²³Te, ¹²⁴Te, ¹²⁵Te, ¹²⁶Te, ¹²⁸Te, and ¹³⁰Te with averaged terrestrial abundances of 0.096%, 2.60%, 0.91%, 4.82%, 7.14%, 19.0%, 31.7%, and 33.8%, respectively (Böhlke et al. 2005). Tellurium isotopes are produced by stellar nucleosynthesis of the p-process (¹²⁰Te), the s-process (¹²²Te, ¹²³Te, ¹²⁴Te, ¹²⁵Te, ¹²⁶Te), and the r-process (¹²⁵Te, ¹²⁶Te, ¹²⁸Te, ¹³⁰Te). Six out of eight Te isotopes were produced by single nucleosynthetic processes (p-process: ¹²⁰Te, s-process: ¹²²Te, ¹²³Te, ¹²⁴Te, r-process: ¹²⁸Te, ¹³⁰Te). Similar to Sn isotopes, the mix of nucleosynthetic production processes makes Te highly advantageous for studying the nucleosynthetic contributions to individual meteorites. The isotopic composition of Te is also affected by the decay of the short-lived nuclide ¹²⁶Sn to ¹²⁶Te, with a half-life of 234.5 kyr. Tin-126 is generated mainly by the r-process. If ¹²⁶Te excesses correlating with Sn/Te ratios are observed in meteorites, it will provide a tight constraint on early Sn-Te fractionation in the protoplanetary disk. As is the case for Cd and Sn, high-precision Te isotope analysis became available with the development of MC-ICP-MS (Lee and Halliday 1995; Fehr et al. 2004). Compared to conventional TIMS techniques, Fehr et al. (2004) improved the precision of ^122–130Te/¹²⁸Te by about one to two orders of magnitude. A comparable precision was obtained by recent N-TIMS technique (Fukami and Yokoyama 2014).

High precision Te isotope data for meteorites have been obtained using MCICP-MS (Fehr et al. 2004; Fehr et al. 2005). In these two studies, the authors examined bulk aliquots of seven carbonaceous chondrites (CI, CM1/2, CM2, two CV3, CO3.5, CK4), three ordinary chondrites (H5, L3.7, LL6), and one enstatite chondrite (EH4), as well as metal and sulfide phases present in iron meteorites (IAB, IC, IIAB). No isotope anomalies were found for any Te isotopes in any of these samples, even for CI and CM chondrites, which contain acid resistant presolar grains (Fig. 19). Although the authors digested chondrite samples using a high-pressure asher (HPA-S Anton Paar) with a mixture of HCl and HNO₃, followed by normal acid digestion with HF, this method was likely not as effective as alkali fusion digestion with respect to dissolving presolar SiC. Thus, the Te data contrast with the Os isotopic data for which acid-digested bulk chondrites exhibited apparent Os isotope anomalies, whereas the same samples decomposed via alkali fusion presented no Os isotope anomalies (Brandon et al. 2005; Yokoyama et al. 2007, 2010). Therefore, the homogeneous Te isotope composition in chondrites and iron meteorites most likely indicate that Te isotopes were homogeneously distributed in the solar nebula, and the effect of incomplete dissolution of acid resistant presolar grains is negligible for the resulting Te isotope compositions. As discussed in the next section, this conclusion is reinforced by the observation that sequential acid leachates of carbonaceous chondrites also have shown no detectable Te isotope anomalies (Fehr et al. 2006).

Figure 19.

μ¹²⁶Te values for CAIs, chondrites, and iron meteorites. Error bars are 2 SE for samples with multiple analyses or the external reproducibility (2 SD) of Te standard measurements for samples with single isotopic run. Note that the error bar for CAI is significant (~500 ppm) and omitted in this.

INTERNAL ISOTOPE ANOMALIES PRESENT IN CHONDRITES

As seen in the previous section, the extent of isotope anomalies for siderophile and chalcophile elements in bulk aliquots of meteorites, if present, are only marginally higher than the level of analytical precision (within a few ε) for individual isotope ratios. One important observation is that acid-digested bulk chondrites exhibited resolvable Os isotope anomalies, whereas the same samples processed using an alkali fusion total digestion method displayed no detectable Os isotope anomalies (Yokoyama et al. 2010). This strongly suggests the existence of siderophile element-rich, acid resistant, isotopically anomalous phase(s) within the chondrites. Thus, as shown previously via analysis of individual presolar grains, selective digestion of chondrite phases provides strong evidence that chondrites are composed of multiple phases with intrinsic isotope compositions which are dramatically different from those of bulk rocks.

In addition to direct isotopic measurement of presolar grains using SIMS/RIMS, two approaches have been recognized as useful methods for detecting internal nucleosynthetic isotope anomalies in chondrites using TIMS and MC-ICP-MS; 1) physically separating CAIs from carbonaceous chondrites and analyzing the isotopic compositions of target elements after chemical purification, and 2) performing sequential acid dissolution of chondrites and subsequent examination of the resulting leachates and acid residues. The extent of isotope anomalies observed in CAIs and acid leachates/residues for many elements are projected to be much larger than observed for bulk samples. These materials, therefore can be highly useful for examining the characteristics of multiple nucleosynthetic components hidden in meteorites. Here we review the progress in the measurement of isotope anomalies in these types of materials for siderophile and chalcophile elements using TIMS and MC-ICP-MS. We also introduce the application of the correlated isotope anomalies for better constraining the composition of s-process nucleosynthesis.

CAIs

CAIs are millimeter- to centimeter-sized lithic, refractory inclusions. CAIs are found in most types of carbonaceous chondrites, especially the CV and CO groups, in which the abundances of refractory inclusions can reach ~10% (Scott and Krot 2003). CAIs are the earliest known condensates formed from a hot nebular gas. Based on the mineral chemistry, CAIs were subdivided into two groups Type A and B in a classic study by Grossman (1975). Type A CAIs contain 80–85% melilite, 15–20% spinel, 1–2% perovskite, and minor minerals including plagioclase and hibonite. Type B CAIs contain 35–60% pyroxene, 15–30% spinel, 5–25% plagioclase, and 5–20% melilite. The timing of the oldest CAI formation has been dated to be 4567.2–4568.2 Ma (Amelin et al. 2010; Bouvier and Wadhwa 2010; Connelly et al. 2012). Since the 1970s, CAIs have been known to possess isotope compositions different from their host chondrites for a variety of refractory elements including Ca, Sr, Ba, Nd, and Sm, especially for the subset of rare CAIs known as Fractionation and Unknown Nuclear effect (FUN) inclusions (e.g., Lee et al. 1978; McCulloch and Wasserburg 1978a,b; Papanastassiou and Wasserburg 1978). For example, very low ⁸⁴Sr/⁸⁶Sr ratios (–0.4‰ relative to a terrestrial standard) are found in some FUN CAIs (Papanastassiou and Wasserburg 1978).

More recently, high precision isotope analyses for some heavy elements revealed that nucleosynthetic isotope anomalies are ubiquitous in normal CAIs as well (e.g., Brennecka et al. 2013). A prominent example of the high precision isotope analysis of CAIs for siderophile and chalcophile elements is Mo. Yin et al. (2002) analyzed one type B CAI from the Allende meteorite and found an r-process-enriched pattern with ε⁹⁵Mo ≈ ε¹⁰⁰Mo = ~+2 (Fig. 20). As shown in Figure 20, very similar patterns were also obtained for another type B, and one type A CAIs from Allende (Becker and Walker 2003a). These patterns are, however, slightly different from that for presolar SiC X-grains from supernovae (Fig. 8b), which show relatively small anomalies in ε¹⁰⁰Mo, leading these authors to conclude that carbonaceous chondrites contain multiple nucleosynthetic components inherited from diverse supernova sources (Fig. 20). Burkhardt et al. (2011) subsequently conducted Mo isotope analyses of five type B CAIs from Allende with higher precision, and obtained patterns with clear kinks at ε⁹⁴Mo, indicative of the enrichment of an r-process component (Fig. 20). However, the CAI data deviate from mixing lines between the terrestrial component and a putative r-process component (Arlandini et al. 1999) in εⁱMo–ε⁹²Mo space (Fig. 14). In addition, one peculiar CAI, most likely a fluffy type A inclusion, exhibited much larger positive Mo isotope anomalies (ε⁹²Mo ~+22; Fig. 20), without a ε⁹⁴Mo kink, indicating an s-process deficit rather than an excess r-process component. The authors concluded that the relatively homogeneous Mo isotope anomalies in five type B CAIs most likely arose from a late injection of freshly synthesized material to the nebula that was enriched in neutron-rich isotopes, as is consistent with other isotope systems, such as Ti, Cr, Ni, Zr, Ba, and Nd (McCulloch and Wasserburg 1978a; Niemeyer and Lugmair 1981; Birck and Allègre 1984; Birck and Lugmair 1988; Schönbächler et al. 2003). The injected material must have had a Mo isotopic composition either slightly different from that estimated by the s-process model of Arlandini et al. (1999), or enriched both in r- and p-process components. By contrast, the exceptional signature of an s-process deficit in one CAI may be the result of condensation from a nebular material which preserved an early isotopic heterogeneity.

Figure 20.

Molybdenum isotope compositions in (a) Type A CAIs and (b) Type B CAIs. Data Sources: [1] Becker et al. (2003a), [2] Yin et al. (2002), [3] Burkhardt et al. (2011). Error bars are the internal precision of individual isotopic run for samples with single measurement.

Chen et al. (2010) determined Ru isotope compositions in three coarse-grained and one fine-grained type B CAIs from Allende. Although the fine-grained CAI did not show Ru isotope ratios resolvable from the terrestrial, three coarse-grained CAIs exhibited negative anomalies exclusively for ε¹⁰⁰Ru (–1.6 ε on average; Fig. 15). The anomalies are due either to an s-process deficit or enrichments of r- and p-process components, which is generally consistent with Mo isotope compositions in CAIs.

Burkhardt et al. (2008) conducted precise W isotope analyses for bulk samples and mineral separates from several type A and type B CAIs from Allende, some of which were also examined for Mo isotopes, as described above. Unlike the Mo results, most of the investigated CAIs have relative proportions of ¹⁸³W, ¹⁸⁴W, and ¹⁸⁶W that are indistinguishable from those of bulk chondrites and the terrestrial standard, although a few samples exhibited ¹⁸⁴W/¹⁸³W ratios ~1 to 2.5 ε units lower than the terrestrial value. The anomalous data most likely reflect an overabundance of r-process relative to s-process isotopes, although the extent of W and Mo isotope anomalies in the same samples were not correlated with each other.

Fehr et al. (2009) analyzed Te isotope compositions in bulk samples and acid leachates from five Allende CAIs. The authors discovered minor differences in the Te isotope compositions for these samples relative to the terrestrial standard and bulk Allende, indicative of the presence of small deficits in r-process or excess in s-process isotopes of Te. However, such nucleosynthetic anomalies were barely resolvable from the terrestrial values, given the analytical uncertainties, and will require further investigation with higher analytical precision.

High precision stable Os isotope data for CAIs are also rare. Yokoyama et al. (2009) examined two coarse-grained Allende CAIs, and found that none of the CAIs had Os isotopic anomalies that were resolvable from the solar values (Fig. 18). Similarly, Archer et al. (2014) analyzed one group I and one group II CAI from Allende and found no resolvable anomalies.

Overall, isotope anomalies of siderophile and chalcophile elements in CAIs have been unambiguously documented for only Mo and Ru (and most likely for W to some extent), both of which are characterized by potential r-process enrichments. This is in agreement with the isotope anomalies of Sr and Zr in CAIs, both of which exhibit excess r-process signatures. Brennecka et al. (2013) noted that the magnitude of anomalies present in Sr, Mo, Ba, Nd, and Sm for eleven CAIs from Allende strongly depend on the atomic mass. With the addition of literature data for Zr and Ru isotope compositions in CAIs, the authors argued that isotopes lighter than mass 140 had r-process excesses, whereas isotopes greater than mass 140 had r-process deficits. Such marked change at an A of ~ 140 suggests a difference in the formation process of the r-process nuclides where A < 140 and A > 140. As noted earlier, ccSNe are responsible for the origin of lighter r-process nuclides, whereas another process such as neutron star mergers could be the sources of heavier r-process nuclides. If true, however, a question remains why some elements such as Te, Os do not follow the rule proposed by Brennecka et al. (2013). More importantly, although isotopic variations for Mo and W are observed in CAIs with different lithologies, it is not clear whether isotopic variability exists within a single CAI for any elements. Precise isotopic measurements of multiple elements in individual CAIs with detailed mineralogical descriptions would shed light on the extent of isotope homogeneity/heterogeneity in the early Solar System at the time of CAI formation.

Acid leachates and residues

Sequential acid leaching is known to be a useful approach for identifying internal nucleosynthetic isotope anomalies in chondrites. It is a form of chemical mineral separation and can concentrate diverse presolar grains with different acid resistance into individual leaching fractions. In fact, the first discovery of presolar grains was made by the analysis of rare gas isotopes in the acid residues of a primitive chondrite (Lewis et al. 1987), and various types of acid resistant presolar grains have been extracted from the acid digestion residues of individual chondrites (Huss et al. 2003). As summarized below, high precision isotope analyses of siderophile and chalcophile elements for chondritic acid leachates and residues have been conducted for Mo, Te, W, and Os since 2002. The typical approach of such studies has been to successively acid leach a chondrite sample in multiple steps proceeding from weak leaching conditions (dilute acid, lower temperature, shorter time) to harsh leaching conditions (concentrated acid, higher temperature, longer time), in order to concentrate as many distinct types of presolar phases as possible. Table 3 shows an example of a six-step acid leaching procedure used to separate Os from a carbonaceous chondrite (Reisberg et al. 2009). In this case, the particular phases targeted by the stepwise leaching included sulfides, carbonates, and fine-grained matrix minerals, including amorphous glass in the first two steps (steps 1–2), metal and tiny olivine grains in step 3, and more acid-resistant phases (e.g., pyroxenes, oxides) in the later steps (steps 4–6). Most of the studies discussed used similar stepwise leaching procedures.

Table 3.

An example of sequential acid leaching procedure applied to ~16.5 g of Murchison meteorite in Reisberg et al. (2009).

Step	Reactants	Time	Temp.
Step 1	50 mL 30% CH3COOH + 50 mL H2O	1 day	20 °C
Step 2	25 mL 16 M HNO3 + 50 mL H2O	5 days	20°C
Step 3	30 mL 12 M HCl + 35 mL H2O	1 day	75°C
Step 4	30 mL 30 M HF + 15 mL 12 M HCl + 15 mL H2O	1 day	75°C
Step 5	10 mL 30 M HF + 10 mL 12 M HCl	3 days	150°C
Step 6	2 mL 16 M HNO3 + 2 mL 30 M HF	15 hours	120°C

Step 6 is applied to a fraction of Step 5 residue)

Molybdenum.

Dauphas et al. (2002b) performed precise Mo isotope analysis for acid leachates obtained by four-step acid leaching of two carbonaceous chondrites, Allende (CV3) and Orgueil (CI1). The authors found that the four leachates of Allende presented W-shaped Mo isotopic patterns which are essentially the same as that of bulk Allende, revealing no internal isotopic heterogeneity in this meteorite (Fig. 21a). By contrast, two out of the four leachates from Orgueil indicated the existence of two distinctive phases for Mo isotopes; a W-shaped pattern in step 2 indicative of s-process deficit, and an M-shaped pattern in step 3 which mirrors the pattern in step 2 (Fig. 21b). The authors concluded that one particular nucleosynthetic carrier phase cannot account for the Mo isotopic signature observed in the step 2 leachate, because the coincidental coupling of p- and r-process enrichments in a single presolar phase is unrealistic for generating the observed s-process deficit. The carrier of the M-shaped pattern in step 3 is most likely mainstream presolar SiC grains, although SiC is known to be significantly acid resistant. The authors speculated that the sequential acid leach did not destroy SiC grains but altered the surface morphology, which enabled leaching of MoC inclusions within SiC. However, it should be noted that SiC grains are not the only carriers of pure s-process Mo. As noted earlier, Nicolussi et al. (1998b) found s-process Mo isotope signatures in presolar HD graphite grains, which would be more susceptible to acid dissolution than SiC grains. Although presolar graphite is less abundant than SiC in carbonaceous chondrites, the contribution of s-process-enriched presolar graphite grains in the step 3 leachate is conceivable.

Figure 21.

Molybdenum isotope compositions in acid leachates from (a) Allende, (b) Orgueil, and (c) Murchison. Data sources: Dauphas et al. (2002a, 2002b), Burkhardt et al. (2012b). Error bars are the internal precision of individual isotopic run for samples with single measurement.

Burkhardt et al. (2012b) carried out Mo isotope analyses for acid leachates from Murchison (CM2). The samples analyzed were the aliquots of leachates prepared by Reisberg et al. (2009) (Table 3), although the final residue remaining after step 5 was first fused by CO₂ laser under a reducing atmosphere (Burkhardt et al. 2011), then digested in HNO₃-HF-HClO₄ to completely dissolve acid resistant presolar grains. Similar to the result of Orgueil, the Murchison leachates exhibited the patterns of s-process deficits in the earlier leaching steps (steps 1–3), and those with s-process excesses in the later leaching fractions (steps 4–6) (Fig. 21c). In particular, the largest positive and negative εMo values were obtained from the first leachate (ε⁹²Mo = +30.5) and the final residue (ε⁹²Mo = −79.3), respectively. The εⁱMo vs. ε⁹²Mo plots clearly indicate that at least two components must be present in this meteorite to account for the observed covariations. The authors concluded that the carrier of an s-process-enriched component, which plotted somewhere on the correlation lines beyond the step 6 data, was presolar SiC, whereas the s-process-depleted component represented by the step 1 leachate data most likely reflected a homogenized nebular component.

Tungsten.

Burkhardt et al. (2012a) determined W isotope compositions in the same acid leachates of Murchison used for Mo and Os isotope analyses (Burkhardt et al. 2012b), and revealed significant internal W isotope variations within this meteorite that reflect a heterogeneous distribution of s- and r-process components (Fig. 22). As was the case of Mo, the first leachate (step 1) released elevated ¹⁸²W/¹⁸⁴W and ¹⁸³W/¹⁸⁴W ratios relative terrestrial values (ε¹⁸²W = +2.81, ε¹⁸³W = +3.62), indicating a deficit of s-process W isotopes in this fraction. Conversely, the later fraction was characterized by negative ε¹⁸²W and ε¹⁸³W values, especially for the final residue (ε¹⁸²W = −25.48, ε¹⁸³W = −15.28), which generally match the pattern of mainstream SiC grains (Ávila et al. 2012). As a result, a positive correlation is observed in a plot of ε¹⁸²W versus ε¹⁸³W. Burkhardt et al. (2012b) concluded that the Mo and W isotope compositions of the different leach steps of Murchison broadly correlated, as expected from s-process nucleosynthesis, indicating that presolar Mo and W are most likely hosted in the same carriers.

Figure 22.

Tungsten isotope compositions in acid leachates from Murchison. Data source: Burkhardt et al. (2012a). Error bars are the internal precision of individual isotopic run for samples with single measurement.

Osmium.

Unlike Mo and W, no Os isotope anomalies have been found in bulk aliquots of chondrites and differentiated meteorites. However, the existence of internal Os isotope heterogeneity has been identified for a variety of chondrites. The six-step leaching experiment of Reisberg et al. (2009) revealed large internal Os isotope anomalies of nucleosynthetic origin (ε¹⁸⁴Os from −108 to +460; ε¹⁸⁶Os from −14.1 to +12.6; ε¹⁸⁸Os from −2.6 to +1.6; ε¹⁹⁰Os from −1.7 to +1.1). The Os isotope anomalies are correlated and form nearly linear trends in εⁱOs versus ε¹⁸⁸Os plots (Fig. 23), strongly suggesting the existence of at least two phases with anomalous nucleosynthetic compositions within the meteorite; the s-process-enriched and r-process-enriched components, relative to the terrestrial. Much of the s-process rich Os, however, was released by relatively mild leaching (steps 2–4), as opposed to the results for Mo and W (Burkhardt et al. 2012b), which were characterized by the strongest s-process-enrichments in the final residue, most likely due to the incorporation of mainstream presolar SiC. Moreover, the enrichments of r-process isotopes were observed in both steps 1 and 5 leachates. These results indicate the presence of multiple distinct presolar phases, with anomalous nucleosynthetic compositions in the Murchison meteorite. The authors pointed out that the enrichment of s-process Os in early leaching fractions was not caused by the dissolution of s-process rich presolar SiC, but was due either to the dissolution of a readily leachable, unidentified presolar phase enriched in s-process Os, or to the existence of a complementary, chemically resistant r-process-rich phase that was not dissolved by these leaching steps. In addition, the authors also speculated upon the existence of p-process rich presolar grains to account for elevated ε¹⁸⁴Os values observed in some leach fractions.

Figure 23.

Osmium isotope anomalies in acid leachates from Murchison. L1–L6 indicate leaching steps. Data source: Reisberg et al. (2009). Error bars are the internal precision of individual isotopic run for samples with single measurement.

Yokoyama et al. (2007, 2010) conducted Os isotope analyses for acid leachates and residues of not only carbonaceous, but also ordinary chondrites. These authors specifically focused on: 1) early leachates of bulk meteorites, 2) the residues enriched in insoluble organic matter (IOM) extracted via demineralization of chondrites, and 3) acid leachates and residues of the IOM-rich fraction. The IOM-rich residues were prepared by a relatively mild, low temperature leaching of the bulk meteorites with CsF/HF (Cody and Alexander 2005), preserving a larger amount of presolar grains compared to the final residues of sequential acid leaching. As shown in Figure 24, nearly all IOM-rich residues exhibit s-process rich Os isotope signatures due to the incorporation of s-process-enriched carriers such as presolar SiC. The extent of s-process enrichment is generally in the order of the petrologic grade of host chondrites (CI1 > C2-ung > CM2 > CR2 ≈ C2/3 > CV3 ≈ L3.05). The change in the pattern of the Os isotope anomalies across the chondrite groups is evidently controlled by the abundance ratio of an s-process-rich phase vs a normal phase with solar Os isotope composition in the IOM-rich residues. Compared to type 3 chondrites, type 1 and type 2 chondrites well preserve presolar grains because of the lack of destructive thermal metamorphism on their parent bodies. On the other hand, relative to residues from CI chondrites, type 2 residues would be slightly, and type 3 significantly, enriched in high temperature components with a solar Os isotopic composition that survived acid dissolution (e.g., Os-alloy, chromites, and Mg-rich spinels). As opposed to IOM residues, early leachates of bulk chondrites are characterized by negative εOs values that are indicative of the enrichment of r-process Os isotopes, which complement the s-process enrichments in IOM-residues (Fig. 24). By contrast, the leachates of IOM-residues exhibit both positive and negative εOs values, suggesting the existence of multiple presolar phases within IOM-rich residues. Such phases are variably enriched in s-, r-, and possibly p-process Os isotopes, because the trend generated by leachate samples in a ε¹⁸⁶Osⁱ vs. ε¹⁸⁸Os plot is clearly resolved from that of residue samples.

Figure 24.

Osmium isotope anomalies in (a, b) acid residues and (c, d) acid leachates from carbonaceous and ordinary chondrites. Data are from Yokoyama et al. (2010). Error bars are uncertainties of individual measurements (2 SE). Circle, diamond, and square symbols are residues (filled) and leachates (open) from chondrite samples with petrologic types 1, 2, and 3, respectively. Black bold lines represent mixing lines between a solar component and a presumed s-process component, for which the slopes are 4.84 ± 0.34 for (a,c) and 0.647 ± 0.027 for (b,d). Bold and thin dashed lines in (a, b) are mixing trends for the solar and an s-process component calculated by Reisberg et al. (2009) using the Os MACS values in Mosconi et al. (2006) and Bao et al. (2000), respectively. Gray thin lines in (c, d) represent regressions of leachate samples with 2σ error envelope (gray dashed curves).

This approach was further extended to evaluate the effects of nebular and parent body processes on presolar components in chondrites (Yokoyama et al. 2011). The authors determined Os isotope compositions in IOM-rich residues separated from type 1 and type 2 carbonaceous chondrites that were subjected to varying degree of aqueous alteration on their parent bodies. They also examined residues from enstatite chondrites, which formed under markedly reduced redox conditions, compared to carbonaceous and ordinary chondrites. All the IOM-rich residues analyzed were characterized by positive εOs values, indicative of excess s-process isotopes (Fig. 25). Similar to the previous study, the magnitude of positive εOs values in the IOM-rich residues from carbonaceous chondrites was in the order of petrologic grade of the host meteorites (type 1 > type 2 > type 3). More importantly, this trend existed even within a single chondrite group; i.e., CR1 > CR2 and CM1 > CM2. The authors concluded that the isotopic variation in IOM-rich residues from type 1–2 chondrites was caused by the selective destruction, during aqueous alteration on their parent bodies, of presolar grains enriched in r-process Os, most likely either presolar silicates or other unidentified, reduced presolar phases, such as metal alloys, carbides, and silicides. On the other hand, the IOM-rich residues from type 3–4 enstatite chondrites have larger positive εOs values than those of carbonaceous and ordinary chondrites that experienced the same degree of thermal metamorphism. This argues for the preservation of s-process-rich presolar grains in enstatite chondrites during heating events under reduced conditions, either while components formed in the nebula, or on their parent bodies.

Figure 25.

Osmium isotope anomalies in acid residues from carbonaceous, ordinary and enstatite chondrites. Data are from Yokoyama et al. (2011). Error bars are uncertainties of individual measurements (2 SE). Bold lines are regressions of data for acid residues from ten primitive chondrites obtained in Yokoyama et al. (2010) which represent mixing lines between solar component and presumed s-process component.

Overall, chondrites possess significant internal Os isotope anomalies as documented in their acid leachates and residues. To account for the uniform, terrestrial Os isotope composition in bulk chondrites, any destructive processes of isotopically anomalous presolar components in the nebula or on the parent bodies did not lose the released component but re-incorporated into a new phase(s) so as not to modify the bulk isotopic composition. However, this might not be the case for elements which have different volatility and/or chemical characteristics compared to Os.

Tellurium.

The features of Te isotope compositions in chondritic acid leachates are markedly different from what are observed for Mo, W, and Os. Fehr et al. (2006) analyzed Te isotope compositions with MC-ICP-MS in sequential acid leachates from three carbonaceous chondrites, Orgueil, Murchison, and Allende. The leaching procedure sequence was acetic acid, HNO₃, HCl, HF-HCl, and HF-HNO₃. Unlike Mo, W, and Os, no sign of isotope anomalies were detected in the abundances of p-, s-, and r-process nuclides for leachates from the three chondrites, excluding a nitric acid fraction of Murchison, which showed an elevated ¹³⁰Te/¹²⁶Te ratio (ε¹³⁰Te = +3.5 ± 2.5) indicative of a small excess of the r-process nuclide. The general absence of isotope anomalies in chondritic acid leachates is inconsistent with the results not only for Mo, W and Os, as noted above, but also for Cr, Zr, and Ba (Rotaru et al. 1992; Hidaka et al. 2003; Schönbächler et al. 2005). The authors concluded that the reason for this mismatch was unclear, but it might reflect volatility and more efficient mixing of Te in the solar nebula.

By contrast, Fukami et al. (2013) performed Te isotope analyses of acid leachates and residues with N-TIMS for Allende, Murchison, and Tagish Lake (C2-ung). The leaching method was the same as described by Reisberg et al. (2009) (Table 3), except that that the final residue remaining after step 6 was first combusted at 1000 °C in a sealed quartz glass tube, then digested with HF-HNO₃ in a high pressure digestion system to completely dissolve refractory presolar grains such as SiC. All but one of the leachate samples were characterized by Te isotopic compositions that were indistinguishable from the terrestrial values. An exception was the final residue of Allende which showed a low ¹³⁰Te/¹²⁸Te ratio compared to the terrestrial value (ε¹³⁰Te = −33±17). Presolar SiC does not account for the observed anomaly because the final residues from Murchison and Tagish Lake showed no Te isotope anomalies resolvable from the terrestrial composition, and these meteorites are known to contain more presolar SiC than Allende. Fukami and Yokoyama (2014) concluded that the Te isotope composition of the final residue of Allende could be reproduced either by depletion of the r-process component (Maas et al. 2001), or by incorporation of an anomalous component represented by that in nanodiamond (Richter et al. 1998). The final residue (nanodiamond) fraction of Allende does not exhibit distinctive isotope anomalies for Mo (Dauphas et al. 2002b), Sr (Yokoyama et al. 2015), or Os (Yokoyama et al. 2007), but evidently shows Xe isotope anomalies (Lewis and Anders 1988). Again, the reason for the discrepancy may be related to the volatility of individual elements, although the details remain unclear.

Isotopic constraints on the s-process nucleosynthetic component

As described above, precise isotopic analyses of Mo, W, and Os in acid leachates, acid residues, and CAIs from chondrites reveal that chondrites possess internal nucleosynthetic isotope anomalies of varying degrees. A common feature is that the extent of isotope anomalies between different isotope pairs with a common denominator are mutually correlated across different sample fractions, forming straight lines in three isotope plots, which generally represent the binary mixing of a nearly pure s-process carrier phase and a terrestrial component. Unlike SIMS and RIMS techniques, analyses of chondrite constituents do not directly provide the endmember isotopic composition of an isotopically anomalous carrier phase (e.g., SiC). However, the slope of the correlation line in a three isotope plot allows calculating the ratio of two numerator isotopes of the putative s-process carrier phase. This further enables evaluating the physical conditions for the nucleosynthetic site of the s-process, as well as the discussion of unstable s-process branching.

Brandon et al. (2005) determined the ¹⁸⁶Os/¹⁸⁸Os ratio of an s-process rich end-member component residing in chondrites to be ~0.48 using the slope of inter-correlation between ε¹⁸⁶Osⁱ and ε¹⁸⁸Os obtained from the analyses of chondrite samples. This value is substantially lower than the theoretical solar s-process ratio of ~0.68 (Beer et al. 1997). Brandon et al. (2005) proposed that the lower s-process ¹⁸⁶Os/¹⁸⁸Os ratio was generated by increased branching at ¹⁸⁶Re, due to an elevated stellar neutron density of 6 × 10⁸ n/cm³ under the conditions of the main s-process in AGB stars, where a neutron is released by the ¹³C(α, n)¹⁶O reaction at T = ~1 × 10⁸ K. Alternatively, it would be produced by the weak s-process that occurs in massive stars via the reaction of ¹³C(α, n)¹⁶O at T = ~3 × 10⁸ K, assuming a neutron density of 10 × 10⁸ n/cm³.

Such a high neutron density at the s-process nucleosynthetic site was challenged by Yokoyama et al. (2007) who pointed out that the neutron density estimated from the other important s-process paths (e.g., Nd–Pm–Sm, Er–Tm–Yb and Os–Ir–Pt) was inconsistent with that proposed by Brandon et al. (2005). Yokoyama et al. (2010) reevaluated s-process nucleosynthesis for Os using the ε¹⁸⁶Osⁱ, ε¹⁸⁸Os, and ε¹⁹⁰Os values of bulk chondrites and their acid residues, and obtained the correlation slopes of 4.84 ± 0.34 for ε¹⁸⁶Osⁱ vs ε¹⁸⁸Os vs and 0.647 ± 0.027 for ε¹⁹⁰Os vs. ε¹⁸⁸Os (Fig. 24). In order to compare these values with those of the hypothesized mixing between the terrestrial and s-process components, they applied the following equation derived by Dauphas et al. (2004) which governs the mixing line in an εⁱOs–ε¹⁸⁸Os diagram plotting chondrite data obtained via N-TIMS analysis with mass fractionation correction using a fixed, solar ¹⁹²Os/¹⁸⁹Os ratio:

$${\mathrm{\epsilon }}_{\text{Os}}^i=\frac{{\mathrm{\rho }}_{\text{Os}}^i-{\mathrm{\rho }}_{\text{Os}}^{192}\cdot {\mathrm{\mu }}_{\text{Os}}^i}{{\mathrm{\rho }}_{\text{Os}}^{188}-{\mathrm{\rho }}_{\text{Os}}^{192}\cdot {\mathrm{\mu }}_{\text{Os}}^{188}}\times {\mathrm{\epsilon }}_{\text{Os}}^{188}$$ (3)

where

$${\mathrm{\rho }}_{\text{Os}}^i={\left(\frac{{}^i\text{Os}}{{}^{189}\text{Os}}\right)}_{s-\text{process}}/{\left(\frac{{}^i\text{Os}}{{}^{189}\text{Os}}\right)}_{\text{solar}}-1$$

$${\mathrm{\mu }}_{\text{Os}}^i=(i-189)/(192-189)$$

By applying these equations, they obtained 6.47 and 0.64 for the mixing lines of ε¹⁸⁶Os–ε¹⁸⁸Os and ε¹⁹⁰Os–ε¹⁸⁸Os, respectively, using the parameters of a “stellar model” for s-process nucleosynthesis (Arlandini et al. 1999). This indicates that the ¹⁹⁰Os/¹⁸⁸Os ratio in the projected s-process component is in good agreement with the theoretical value, whereas the s-process ¹⁸⁶Os/¹⁸⁸Os ratio obtained from chondrite data is lower than the theoretical value. Yokoyama et al. (2007) concluded that the mismatch could be explained either by another s-process path to produce ¹⁸⁷Re through the relatively long-lived isomer of ¹⁸⁶Re (T_1/2 = 2.0 × 10⁵ yr) (Hayakawa et al. 2005; Meyer and Wang 2007), or by errors in the input parameters to the nucleosynthetic calculations. For example, the Maxwellian-averaged neutron capture cross sections (MACS; σ_n) of ¹⁸⁶Os, ¹⁸⁷ n Os, and ¹⁸⁸Os from Mosconi et al. (2006) yield lower s-process ¹⁸⁶Os/¹⁸⁸Os ratios than the earlier parameters used in Arlandini (1999) or Bao et al. (2000). Two follow-up studies (Reisberg et al. 2009; Yokoyama et al. 2010) reached the same conclusion that the hypothetical mixing between the terrestrial and s-process components reproduced well the ¹⁸⁶Os/¹⁸⁸Os ratio observed in chondritic acid leachates and residues when the new MACS values of Mosconi et al. (2006) were used.

On the other hand, Humayun and Brandon (2007) proposed that correlated Os isotope anomalies in chondrites can be conversely used for tightly constraining the MACS value of σ_n(¹⁹⁰Os) by combining the σ_n(¹⁸⁸Os) value measured in the laboratory and the s-process ¹⁹⁰Os/¹⁸⁸Os ratio projected by the chondrite data. This is useful because the σ_n(¹⁹⁰Os) was not measured in the study of Mosconi et al. (2006), who gave reliable MACS of ¹⁸⁶Os, ¹⁸⁷Os, and ¹⁸⁸Os that matched the chondrite data as mentioned above. By using the Os isotope data from Brandon et al. (2005) and σ_n(¹⁸⁸Os) = 291±15 mbarn (Mosconi et al. 2006), coupled with the s-process local approximation model (i.e., abundance × cross section = constant), the authors determined the MACS value of σ_n(¹⁹⁰Os) = 249 ± 18 mbarn at a thermal energy of 30 keV. This is ~20% lower than the value of σ_n(¹⁹⁰Os) = 295 ± 45 mbarn reported by Bao et al. (2000).

Subsequently, Reisberg et al. (2009) followed this approach to determine the MACS value of σ_n(¹⁹⁰Os) using their Os isotope data of acid leachates from the Murchison meteorites. Unlike Humayun and Brandon (2007), the authors did not assume the s-process local approximation but applied a full nuclear reaction network calculation, because ¹⁸⁸Os is fed by several branching points in the s-process pathway, in particular ¹⁸⁵W (Fig. 4). In addition, they included the effect of internal mass fractionation correction as presented in Equation (1). Consequently, the authors reported the MACS value of σ_n(¹⁹⁰Os) = 200 ± 22 mbarn, which is lower than that reported by Bao et al. (2000) or that estimated by Humayun and Brandon (2007).

ORIGIN OF PLANETARY SCALE ISOTOPE ANOMALIES IN METEORITES

As seen in previous sections, a variety of nucleosynthetic isotope anomalies have been documented in bulk meteorites and/or chondrite constituents (CAIs, acid leachates and residues) for siderophile elements such as Mo, Ru, W, and Os, yet isotopic anomalies for chalcophile elements such as Cd and Te are either barely resolved, or non-existent. Anomalies are have also been documented in meteorites for lithophile elements including Ti, Cr, Ni, Sr, Zr, Ba, Nd, Sm, as well as the siderophile element Ni (e.g., Schönbächler et al. 2003; Andreasen and Sharma 2007; Regelous et al. 2008; Trinquier et al. 2009; Qin et al. 2011a; Akram et al. 2013). Despite this wealth of data, however, it remains unclear to what extent nucleosynthetic isotope anomalies exist on the global scale of parent bodies of meteorites, and even planets.

A useful approach for elucidating the origin of planetary scale isotope anomalies would be to directly plot and compare the isotopic data of different elements obtained from various meteorite groups. For instance, Warren (2011) found a fundamental dichotomy between carbonaceous chondrites and other meteorites when isotope anomalies for O, Ti, and Cr were plotted in diagrams such as ε⁵⁴Cr–ε⁵⁰Ti and ε⁵⁴Cr–Δ¹⁷O. The author concluded that the isotopic dichotomy was due to the difference in formation location between two groups; non-carbonaceous meteorites accreted in the inner Solar System (sunward relative to Jupiter), whereas carbonaceous chondrites originally accreted in the outer Solar System.

Two models have been proposed to account for the observed heterogeneous distribution of isotopically normal and anomalous components. Dauphas et al. (2010) and Qin et al. (2011b) discovered that the carrier phase of ⁵⁴Cr anomaly in meteorites was nanoparticles (< 100 nm) of Cr-rich spinels with enhanced ⁵⁴Cr/⁵²Cr ratios, which were likely produced by a type II supernova. They argued that the planetary scale ⁵⁴Cr anomaly was caused by late injection of a nearby supernova which scattered ⁵⁴Cr rich nano-grains into the protoplanetary disk, followed by aerodynamic sorting of isotopically normal, coarser grains that resulted in variations in the isotopic abundance of ⁵⁴Cr across planetary materials. This model can potentially explain the correlated isotope anomalies between ⁵⁰Ti and ⁵⁴Cr in bulk chondrites assuming that the carriers of these two neutron-rich isotopes were produced at the same stellar site and had similar grain sizes and chemical properties such that they could not be decoupled during incorporation in planetesimals. Alternatively, Trinquier et al. (2009) proposed that the correlation between ⁵⁰Ti and ⁵⁴Cr in bulk chondrites was the result of selective destruction of thermally unstable, presolar grains in the solar nebula.

As for siderophile elements, Dauphas et al. (2004) discovered that isotope anomalies of Mo (Dauphas et al. 2002a) and Ru (Chen et al. 2010) were well correlated in iron meteorites when bulk measurements were grouped by meteorite classes, forming a straight line on a plot of ε¹⁰⁰Ru–ε⁹²Mo, with the line passing through the origin of the plot which represents the terrestrial composition (Fig. 26). The Mo–Ru trend extends toward the direction of s-process deficit, implying that isotopically anomalous Mo and Ru are hosted in the same s-process-rich carriers, which were distributed in the solar nebula in varying proportions of isotopically normal to anomalous phases. A similar correlation between isotope anomalies of Mo and Ru was also reported for bulk carbonaceous chondrites (Fischer-Gödde et al. 2013), although the slope of the trend in the ε¹⁰⁰Ru–ε⁹²Mo diagram deviates slightly from the theoretical s-process and terrestrial mixing line (Arlandini et al. 1999) (Fig. 26). However, the correlations are not conclusive for discriminating the two models mentioned above; late supernova injection coupled with grain size sorting, and nebular thermal processing.

Figure 26.

Correlation of Mo and Ru isotope anomalies in meteorites. Data are from Dauphas et al. (2004) and Fischer-Gödde et al. (2013).

Burkhardt et al. (2012b) investigated Mo and W isotope compositions in bulk aliquots of meteorites, as well as in chondrite acid leachates and residues. Unlike previous studies, these isotope compositions were all measured by a single research group using the same sample fractions, eliminating the possibility of isotopic inconsistency caused by sample heterogeneity. As noted in the previous section, Mo and W isotope anomalies in chondritic acid leachates were broadly correlated, suggesting that isotopically anomalous Mo and W are likely hosted in the same carriers in chondrites (Fig. 27). However, as opposed to Mo isotopes, most meteorites do not show W isotope anomalies on the bulk scale. The discrepancy of external and internal isotope anomalies for Mo and W isotope suggests that initially homogeneous mixtures of isotopically normal and anomalous dust grains in the solar nebula was disturbed only for Mo, but not for W. The authors concluded that selective removal of volatile Mo oxides occurred due to destructive thermal processing within the solar nebula, resulting in Mo isotope heterogeneity, while refractory W was not affected. This model merits further consideration for explaining why bulk meteorites also do not possess Os isotope anomalies, whereas acid leachates and residues presented significant isotope anomalies for these elements. Reduced Os is similarly refractory to W, so it can perhaps be inferred that the isotopic compositions of Os in bulk meteorites have not been modified via thermal processing.

Figure 27.

Correlation of Mo and W isotope anomalies in meteorites. Data are from Burkhardt et al. (2012b).

Yokoyama et al. (2014) speculated that Te isotope compositions were not fractionated via thermal processing because their moderately volatile nature caused total evaporation of Te during heating, and that this did not create isotopic heterogeneity. In other words, to fractionate Mo isotopes via thermal processing, selective volatilization of isotopically anomalous Mo associated with physical separation of gas and remaining solid must have occurred. If true, isotope anomalies at the bulk meteorite scale can be observed only for elements with a 50% condensation temperature higher than Te (709 K) and lower than W (1789 K). Molybdenum and Ru match this condition, while Cd is more volatile than Te, so that no Cd isotope anomalies were observed in meteorites.

CONCLUDING REMARKS

In the last decade, an increasing amount of highly precise data for isotope anomalies of siderophile and chalcophile elements in a variety of meteorites have been produced by isotope measurements using the latest mass spectrometers. One of the most remarkable findings of these investigations is that isotope anomalies at the bulk meteorite scale do not prevail for all elements, but are limited to elements such as Mo and Ru. By contrast, isotope anomalies for chondrite constituents (CAIs, acid leachates, and residues) are more widespread for elements including Mo, Ru, W, and Os. In general, there are at least two isotopically anomalous carrier phases dominantly residing in chondrites; one is enriched in s-process isotopes, which most likely are represented by the mainstream presolar SiC grains, while the other phase is a complementary component to the s-process-rich material. Some unidentified phases may also be present in chondrites which are enriched or depleted in p-process nuclides, but these phases are evidently minor.

The inter-correlation for the magnitude of isotope anomalies among different elements is useful for identifying the cause of planetary scale isotope anomalies. Correlations for siderophile and chalcophile elements have revealed that thermal processing in the nebula likely caused selective destruction of thermally labile presolar phases and preferential isotope fractionation of moderately refractory elements, such as Mo and Ru, via physical separation of gas and solid. However, other processes such as late injection of supernova associated with grain sorting, or parent body processes including aqueous alteration and thermal metamorphism, must be borne in mind as alternative causes for generating planetary scale isotope anomalies in meteorites.