EMG burst presence probability: a joint time-frequency representation of muscle activity and its application to onset detection

Abstract

The purpose of this study was to quantify muscle activity in the time-frequency domain, therefore providing an alternative tool to measure muscle activity. This paper presents a novel method to measure muscle activity by utilizing EMG burst presence probability (EBPP) in the time-frequency domain. The EMG signal is grouped into several Mel-scale subbands, and the logarithmic power sequence is extracted from each subband. Each log-power sequence can be regarded as a dynamic process that transits between the states of EMG burst and non-burst. The hidden Markov model (HMM) was employed to elaborate this dynamic process since HMM is intrinsically advantageous in modeling the temporal correlation of EMG burst/non-burst presence. The EBPP was eventually yielded by HMM based on the criterion of maximum likelihood. Our approach achieved comparable performance with the Bonato method.

1. Introduction

The detection of muscle activity using surface electromyography (EMG) is one fundamental step in many applications such as motor control (Merlo et al., 2003; Micera et al., 2001), posture and gait analysis(Bonato et al., 1998; Li et al., 2007), and myoelectric control of prosthetic devices(Dalley et al., 2012; Severini et al., 2012). The literature has widely reported various computerized detection techniques of muscle activity onset, in which the most common utilized parameters were associated with the EMG signal amplitude(Bonato et al., 1998; Hodges and Bui, 1996; Santello and McDonagh, 1998). However, most EMG onset detection methods up to now only give EMG burst presence information in the time domain (Hodges and Bui, 1996; Lee et al., 2007; Merlo et al., 2003; Micera et al., 2001; Santello and McDonagh, 1998; Severini et al., 2012; Staude, 2001; Xu et al., 2013), the more detailed information in each frequency component is absent. A novel time-frequency representation is required to investigate the changes in wideband spectral power over time during EMG bursts. Moreover, EMG signal is sparsely distributed in the time-frequency domain, namely not each frequency component is occupied by EMG signals even for EMG bursts are present. Thus, it is required to identify the frequency components of non-burst EMG and further suppress them in the detection of the onset of muscle activity.

Signal presence probability can give a full description of signal presence in the time-frequency domain. This description method was conventionally used for speech signal processing, wherein it was derived from the ratio between the local energy of the noisy speech and its minimum within a specified time window (Cohen and Berdugo, 2002). This ratio-based method subsequently evolved into a Gaussian mixture model (GMM) that consists of speech and non-speech Gaussian models (Cohen, 2003; Rangachari and Loizou, 2006). But the GMM does not consider the temporal correlation of signal power. To overcome this limitation, the hidden Markov model (HMM) has successfully been applied to estimation of speech presence probability (SPP), which has the capability of modeling the temporal correlation (Ying and Yan, 2013). Since the envelope of EMG signal exhibits the temporal correlation, similar to speech signal, HMMs have been applied to modeling the EMG signal (Chan et al., 2002; Chan et al., 2006; Lee, 2008).

The aim of this study was to quantify muscle activity in the time-frequency domain, therefore providing an alternative tool to measure muscle activity. This paper presents a new measure of muscle activity for mitigating the effects of the frequency components of non-burst EMG signals by introducing EMG burst presence probability (EBPP) to characterize the EMG activity.

2. Methods

A. EMG burst presence probability

Motivated by previous SPP estimation studies (Cohen, 2003; Cohen and Berdugo, 2001, 2002; Gerkmann et al., 2008; Rangachari and Loizou, 2006), we estimated the probability of the presence of EMG bursts using a sequential GMM that consists of EMG burst and non-burst Gaussian models. Let s_ℓ = 1 and s_ℓ = 0 respectively indicate the two hypotheses of EMG burst presence and absence in the ℓ th frame, corresponding to the EMG burst and non-burst states.

The GMM is represented as

$$\begin{gathered} p\left(y_{\mathcal{l}}|{\lambda }_{\mathcal{l}}\right)=\sum _{s_{\mathcal{l}}}p\left(y_{\mathcal{l}},s_{\mathcal{l}}|{\lambda }_{\mathcal{l}}\right) \\ =\sum _{s_{\mathcal{l}}}p\left(s_{\mathcal{l}}|{\lambda }_{\mathcal{l}}\right)p\left(y_{\mathcal{l}}|s_{\mathcal{l}},{\lambda }_{\mathcal{l}}\right), \end{gathered}$$ (1)

where y_ℓ represents the logarithmic power in the ℓ th frame, λ_ℓ denotes the parameter set, p(s_ℓ |λ_ℓ) represents the priori distribution of EMG burst presence/absence, and p(y_ℓ | s_ℓ,λ_ℓ) is the conditional probability density function of EMG burst presence/absence, given by

$$p\left(y_{\mathcal{l}}|s_{\mathcal{l}}=i,{\lambda }_{\mathcal{l}}\right)=\frac{1}{\pi {\eta }_{i,\mathcal{l}}}\text{exp}\{-y_{\mathcal{l}}^2/{\eta }_{i,\mathcal{l}}\},$$ (2)

where ${\eta }_{i,\mathcal{l}}\triangleq E\left\{y_{\mathcal{l}}^2|s_{\mathcal{l}}=i\right\}$ denotes the short-term magnitude spectrum of the EMG burst/non-burst components. Accordingly, the EBPP is represented as

$$p_{\mathcal{l}}=\frac{p\left(y_{\mathcal{l}},s_{\mathcal{l}}=1|{\lambda }_{\mathcal{l}}\right)}{p\left(y_{\mathcal{l}}|{\lambda }_{\mathcal{l}}\right)}=\frac{p\left(s_{\mathcal{l}}=1|{\lambda }_{\mathcal{l}}\right)p\left(y_{\mathcal{l}}|s_{\mathcal{l}}=1,{\lambda }_{\mathcal{l}}\right)}{{\sum }_{s_{\mathcal{l}}}p\left(s_{\mathcal{l}}|{\lambda }_{\mathcal{l}}\right)p\left(y_{\mathcal{l}}|s_{\mathcal{l}},{\lambda }_{\mathcal{l}}\right)}.$$ (3)

B. Muscle activity estimation using EMG burst presence probability

Presence of EMG burst in a given frame can be determined by the ratio between the local energy of the noisy EMG and its minimum within a specified time window. Thus, EMG burst and non-burst frequency components can be detected by an EBPP estimator in frequency subands. It follows from (3), the computation of the EBPP requires an estimate for the parameter set λ_ℓ. The algorithm of improved minima controlled recursive averaging (IMCRA) represents the parameter set as a function of the a posteriori and a priori signal-to-noise ratio(Cohen, 2003). Similar to the IMCRA method, the constrained sequential HMM can be used to estimate SPP, which has the capability of modeling the temporal correlation (Ying and Yan, 2013). Specifically, HMMs can model a time sequence of presence/absence of EMG burst as a dynamic process of the transition between EMG burst and non-burst states (Chan et al., 2002; Chan et al., 2006; Lee, 2008)..

Similar to the estimation of SPP in previous studies (Ying and Yan, 2013), the EBPP was derived from the HMM in this study. An HMM considers a log-power sequence in a causal window of L samples, x_ℓ = {x_ℓ−L+1,….x_ℓ}. The logarithmic powers of EMG burst and non-burst are assumed to follow a Gaussian distribution. The transitional dynamics of the power sequence between EMG burst and non-burst states is modeled by a Markov chain, in which the output probability of each state is represented by a Gaussian model. These transition probabilities are estimated from the observed data based on the criterion of maximum-likelihood.

In the succeeding sections, λ_ℓ denotes the parameter set of HMM that is estimated from log-power sequence x_ℓ, and s_ℓ = {s_{ℓ − L+1},…, s_ℓ} represents a state sequence corresponding to x¡. Given a training sequence x_ℓ, a maximum-likelihood estimate of the parameter set λ_ℓ is given by

$${\lambda }_{\mathcal{l}}=\text{arg}\underset{\lambda }{\text{maxln}}\sum _{{\mathbf{s}}_l}p\left({\mathbf{x}}_{\mathcal{l}},{\mathbf{s}}_{\mathcal{l}}|\lambda \right),$$ (4)

. The model parameters were determined using the expectation-maximization (EM) algorithm The HMM probability density function $\sum _{{\mathbf{\text{s}}}_{{}_{\mathcal{l}}}}p\left({\mathbf{x}}_{\mathcal{l}},{\mathbf{s}}_{\mathcal{l}}|{\lambda }_{\mathcal{l}}\right)$ and the mathematical details of the HMM were described in (Ying and Yan, 2013).

The EMG signal was first chopped into a series of frames using a Hanning window (window length: 32 ms, overlapping step: 16 ms). The signal of each frame was subsequently transformed into the frequency domain by the fast Fourier transform (FFT). Then, the signal is grouped into eight Mel-scale subbands by using the logarithmic value of the absolute magnitude sum of included FFT bins, where the boundary for the d-th Mel-scale is given by

$$I_d=700\times \left[\text{exp}\left\{\frac{dm}{2595}\times log10\right\}-1\right]\times N_{FFT}/f$$ (5)

Where f is the sampling frequency, N_FFT is the FFT length, and N_F is the number of the mel - scale subbands, and m is the maximal Mel value, given by

$$m=\frac{2595\times lo{g}_{10}(1+\frac{f}{1400})}{N_F}$$ (6)

The whole band was partitioned into N_F subbands by the boundaries $\left\{{\text{I}}_0,{\text{I}}_1,{\text{I}}_2,\dots ,{\text{I}}_{{\text{N}}_{\mathrm{F}}}\right\}$. Finally, the EBPP was computed at each subband, which describes the EMG burst in the time-frequency domain using energy information along both time and frequency axes. Our method utilizes a one-dimension HMM model on each subband. All HMMs run in parallel.

C. Performance evaluation

The EBPP was examined using both simulated and experimental surface EMG signals to measure muscle activity. A series of EMG signals were simulated at a sampling rate of 2000 Hz by filtering white Gaussian noise with a shaping filter modeling the characteristics of typical surface EMG(Shwedyk et al., 1977; Stulen and De Luca, 1981). The shaping filter is defined as

$$H_{sf}(s)=\frac{ks{\left(2\pi f_h\right)}^2}{\left(s+2\pi f_l\right){\left(s+2\pi f_h\right)}^2}$$ (7)

where s is the Laplace variable, k is a scaling factor. The cutoff frequencies f_l and f_h of the band-pass filter were set to 80 Hz and 120 Hz (Bonato et al., 1998; Vannozzi et al., 2010), respectively. An independently generated zero-mean white Gaussian noise was added to clean EMG signals to simulate surface EMG recordings with different noise levels. The standard deviation of the noise was determined by the noise level resulted in different SNRs (20, 15, 10, 8, 5 and 2 dB, respectively) of the EMG signal. The SNRs were selected according to previous studies (Bonato et al., 1998; Li et al., 2007). For each SNR, 60 trials of signal were generated.

The experimental surface EMG signals were collected from the brachioradialis of one normal control subject with no known neuromuscular disease (31, male) with a Refa EMG system (TMS International B.V., Netherlands). The signal sampling rate was 2000 Hz.

In addition, the performance of the EBPP method was compared with one previous method for muscle activity onset detection. The method is based on the double threshold algorithm (Bonato et al., 1998) (denoted as Bonato method). A two-way ANOVA (factors are SNR and detection method) was performed to determine how much of effects the SNR value and detection method had on the latency.

3. Results

A. Distribution of logarithmic powers in EMG burst and non-burst states

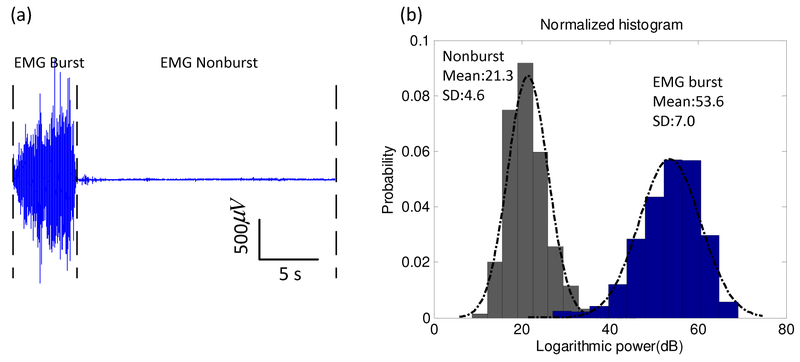
The probability distribution of the logarithmic power amplitudes of burst or non-burst EMG was estimated from a histogram using the aforementioned experimental EMG signals. Fig. 1 shows an example of experimental EMG and the corresponding histograms of logarithmic power amplitudes of the EMG in burst and non-burst conditions, which displays two typical histograms together with two plots of a Gaussian distribution with mean and variance. The logarithmic power amplitudes of burst and non-burst EMG were normally distributed and were fitted by single Gaussian curves (smooth curves) with means at 21.3 and 53.6 dB, respectively. Furthermore, the composite normality of the logarithmic power amplitudes of burst or non-burst EMG was tested using the Lilliefors test (Lilliefors, 1967). The test showed that the logarithmic power amplitudes of burst and non-burst EMG could be assumed to have a Gaussian distribution, at risk of 5%. These results provide quantitative evidence consistent with the hypothesis that the distribution of logarithmic power amplitudes of burst or non-burst EMG closely approximates a Gaussian distribution.

Fig.1.

Comparison of distributions of logarithmic powers in EMG burst and non-burst states. An example of EMG was collected from the brachioradialis of one normal control subject with no known neuromuscular disease (31, male) at a sampling rate of 2000 Hz. The corresponding histograms of logarithmic power amplitudes of the EMG in burst and non-burst states are plotted. Both distributions closely approximate a Gaussian distribution (determined by a Lilliefors test).

B. Results from simulated surface EMG signals

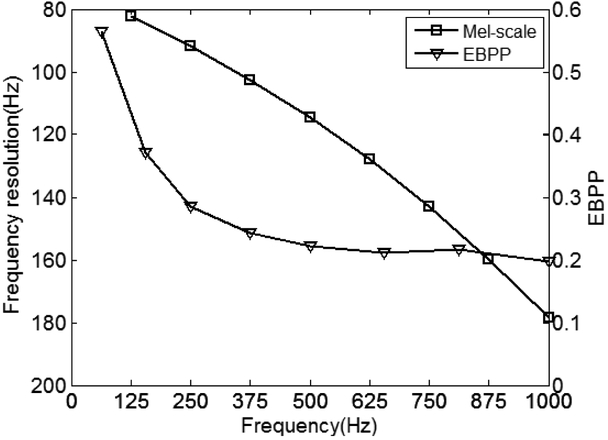
We plot the frequency resolution curves of the Mel frequency warping method in Fig. 2, where the frequency-EBPP curve is also plotted. Fig. 2 shows that the EMG signal is always present with higher probability at low frequency than that at high frequency within the EMG bandwidth, thus the EBPP appears to increase when the frequency of the corresponding EMG signal decreases. These results indicate that the Mel-scale emphasizes the lower frequencies, which distributes linearly and is more meaningful for EMG frequency warping processing than the uniform frequency warping method.

Fig.2.

Comparison of frequency resolutions of filter bands with Mel scale processing and EBPPs across all the frequencies. The EBPP curve uses the scale of the right axis, and the Mel-scale curve uses the scale of the left axis.

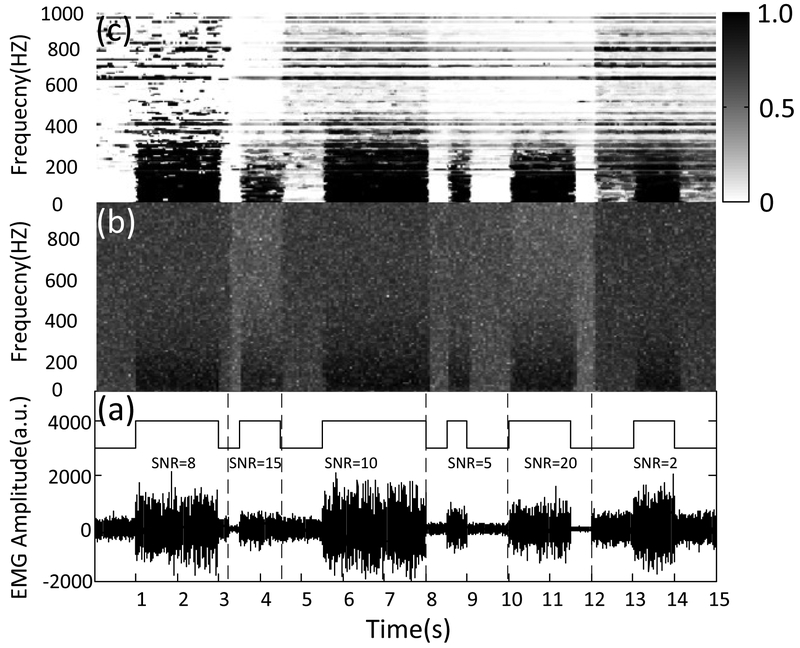
An example of EBPPs from simulated EMG is shown in Fig. 3, where the EBPP (c) and the spectrograms of the EMG signal (b) are presented for an EMG trial corrupted by white noise with different SNR values (a). The probability of EMG burst presence is a time-frequency representation, which has three key quantities including magnitude, frequency and time, thus provides the probability of the presence of an EMG burst at a specific time and frequency. We found that the EBPP demonstrates a consistent but discriminative pattern to detect presence of EMG burst from background noise therefore providing an alternative tool for muscle activity detection. Note that we plotted the EBPP with high frequency resolution instead of using eight Mel subbands to provide a graphical comparison between the EBPP and noisy spectrum.

Fig. 3.

Spectrogram illustrating the EBPP estimated by the sequential HMM method. (a) Superimposing the rectangular envelope built on the basis of the onset/offset to the EMG trace with SNRs. (b) The magnitude spectrogram of the EMG data. (c) The EBPPs obtained from the EMG traces. The transition from white to black associated with the EBPPs corresponds to probability changing from 0 to 1. The two-dimensional representation (color map: dark, high values; white, low values) provides the probability of EMG burst presence at each time instant (x-axis) and frequency (y-axis).

C. Muscle activity detection

The EMG recordings were band-pass filtered between 20 and 500 Hz prior to onset detection using the EBPP and Bonato methods. The onset performance was evaluated by the latency τ, defined as the absolute difference between the true onset time t₀ (e.g. 0.5 s for each testing signal) and the detected onset time t_d:

$$\tau =\left|t_d-t_0\right|$$ (8)

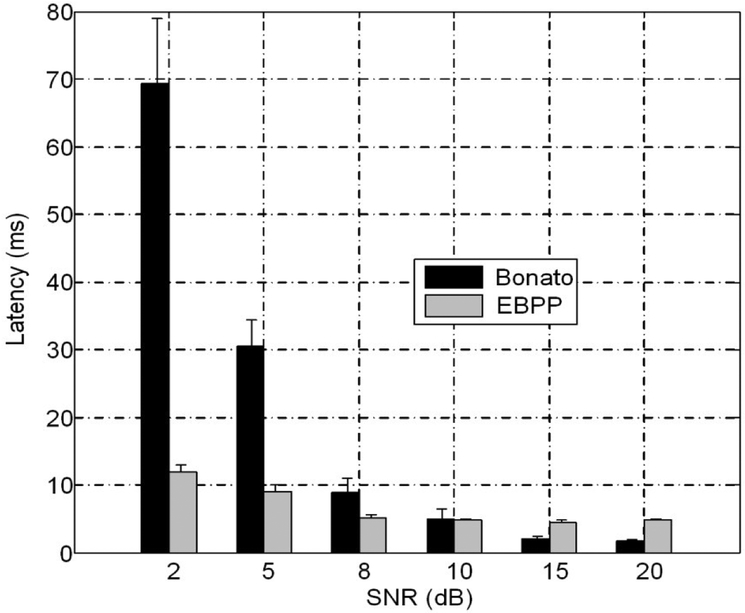
The muscle activity detection performance with different methods is summarized in Fig.4. Although the EBPP has a larger latency at high SNR (around 3–4 ms difference from Bonato), but the EBPP method is more resilient to noise. While the latency increases by 8–9ms for the EBPP when SNR is decreased to 2dB, it increases almost 70 ms for the Bonato method. A twoway ANOVA showed no significant effects. The onset detection performance of all two tested methods was comparable (two-way ANOVA, P> 0.05, for all tested SNRs). In the cases of relatively low SNRs, the method based on EBPP exhibited better performance than the Bonato method, but without significant difference.

Fig. 4.

Comparison of onset detection performance using different methods (mean ± standard error). Bonato: the double threshold algorithm; EBPP: method based on EBPP conditioning. For each SNR level, the mean latency was averaged over 60 trials of simulated surface EMG signals. The EMG recordings were band-pass filtered between 20 and 500 Hz prior to onset detection.

D. Testing of experimental surface EMG signals

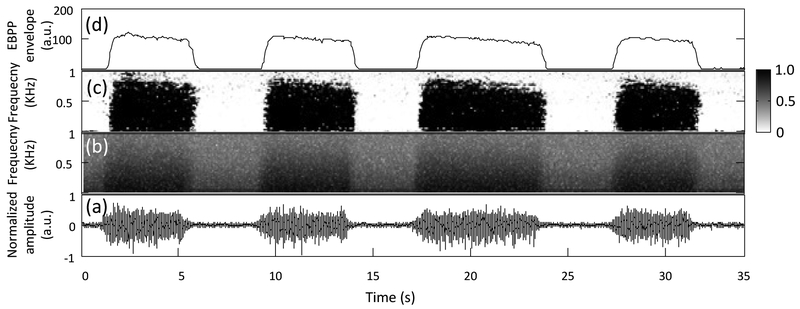
The performance of the proposed method using an experimental surface EMG was demonstrated. An example of the EBPP with high frequency resolution from experimental EMG is shown in Fig. 5, where the EBPPs from the entire Mel-scale subbands were summed to form the envelope for characterizing muscle activation. It is easier to visually determine the EMG onset from the EMG burst spectral structure depicted by the EBPP (Figure 5c) than the spectrograms of the EMG signal (Figure 5b).

Fig. 5.

An experimental EMG recording and the corresponding signal spectra, the EBPPs and the EBPP envelope. (a) A representative EMG trace consisting of four bursts. (b) The magnitude spectrogram of the EMG data. (c) The EBPPs obtained from the EMG data, the transition from white to black associated with the EBPPs corresponds to probability changing from 0 to 1. (d) The EBPP envelope generated from the sum of the EBPP at each Mel-scale subband.

4. Discussion

A novel approach for characterizing muscle activation was presented based on the time-frequency probability computation. The EMG burst presence was represented by EBPP in each subband of the EMG signal. The constrained sequential HMM was employed to model the log-power sequence by taking advantage of the HMM’s capability of modeling the temporal correlation of EMG burst/non-burst. The EBPP was eventually derived from the HMM parameters based on the criterion of maximum likelihood. The performance of the proposed method was examined using both simulated and experimental surface EMG signals. Our results show that the EBPP can effectively detect bursts of EMG by suppressing the interference of frequency components of the non-burst EMG and the EBPP method is resilient to noise.

In this study, exact time-frequency structure has been analyzed with the use of the EBPP analysis for yielding the analysis of EMG signal in the time-frequency domain. We observed that EMG signal is always present with higher probability at low frequency within the EMG bandwidth than at higher frequencies where the EMG power is low (Fig.2). EMG signal is very similar to speech signal at this point (Lu and Dang, 2008). Thus the low-frequency bands should be partitioned with a higher resolution than the high-frequency bands. To emphasize low frequency information of EMG signals, the Mel frequency warping method was used in this study. It should be noted that this study utilizes the Mel scale property of frequency resolution, instead of human auditory perception. We found that Mel-scale is useful to obtain frequency components of EMG recordings to characterize the EMG activity.

HMMs preserve the structural characteristics and temporal ordering of the signal by using a Markov chain topology. Taking this advantage, a sequence of EMG signals can be modelled by HMMs. Previous studies have used HMMs to classify EMG signals in automatic speech recognition systems (Chan et al., 2002; Chan et al., 2006; Lee, 2008). Whereas, the constrained sequential HMM(Ying and Yan, 2013) was utilized in this study to model a time sequence of presence/absence of EMG burst as a dynamic process of the transition between the states of EMG burst and non-burst. Similarly, we estimated the EBPP from the constrained sequential HMM.

SPP estimators have successfully been used in detecting the non-speech frequency components and further suppressing them in speech enhancement (Cohen and Berdugo, 2001, 2002; Gerkmann et al., 2008). An implication of this is the possibility that the EBPP can be used to denoise EMG, further studies are therefore recommended to demonstrate the potential use of the EBPP.