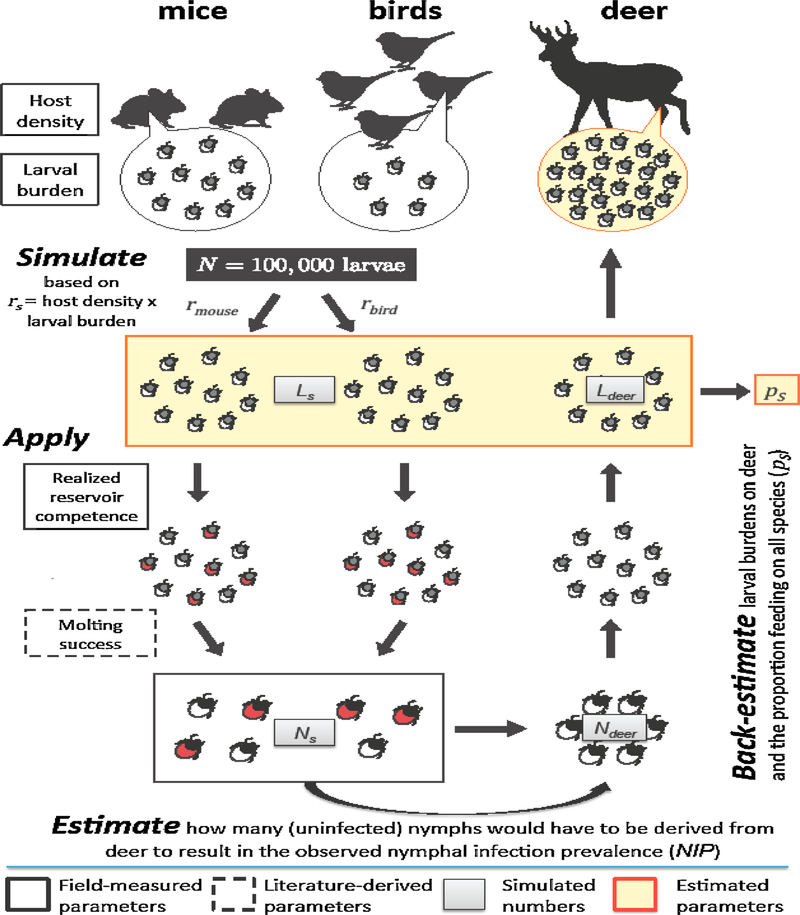
Fig. 1.

Algorithm used to back-estimate the proportion of larvae fed by each host group and the average larval burden on white-tailed deer. We considered a simplified host community with white-footed mice, birds (seven species combined), and white-tailed deer. We simulated N = 100,000 engorged larvae sampled from mice and birds with probability r_mice and r_bird, which is proportional to the product of their densities d_s and average larval burdens b_s (Equation 1 in Supplementary materials). Larvae (L_s) acquire infection according to the measured realized reservoir competence (red tick symbols represent infected larvae) and molt to nymphs (N_s) according to a fixed probability derived from estimated molting success in LoGiudice et al. (2003). We estimated how many (uninfected) nymphs would have to be derived from deer (N_deer) to result in the observed nymphal infection prevalence (NIP; Equation 2 in Supplementary information). The number of engorged larvae feeding on white-tailed deer L_deer and the proportion of larvae feeding on different hosts p_s were calculated after applying the inverse processes of molting and infection (Equations 3 and 4 in Supplementary information). Finally, the number of deer present in an area producing 100,000 engorged larvae was applied to calculate the average larval burden on white-tailed deer (Equation 5 in Supplementary information). These steps were for 10,000 iterations to derive the distributions of density, average larval burden, and proportion of larvae feeding on different hosts, shown in Fig. 2. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article).