Significance
We propose a mechanistic description of fusion of a synaptic vesicle with a target membrane executed by a team of zippering SNARE complexes (SNAREpins). In the context of neurotransmitters release, this process naturally decomposes in two steps with rates that depend on the number of SNAREpins . The first step is synchronized escape from the metastable half-zippered state, which gets exponentially more sluggish as increases. The second step is fusion of two closely tethered membranes, which is accelerated exponentially by an increase of . The tradeoff between these two antagonist trends results in a sharply optimal number of SNAREpins , which ensures fusion at the physiological submillisecond timescale.
Keywords: SNARE, membrane fusion, protein folding, neurotransmitter release, muscle contraction
Abstract
SNARE proteins zipper to form complexes (SNAREpins) that power vesicle fusion with target membranes in a variety of biological processes. A single SNAREpin takes about 1 s to fuse two bilayers, yet a handful can ensure release of neurotransmitters from synaptic vesicles much faster: in a 10th of a millisecond. We propose that, similar to the case of muscle myosins, the ultrafast fusion results from cooperative action of many SNAREpins. The coupling originates from mechanical interactions induced by confining scaffolds. Each SNAREpin is known to have enough energy to overcome the fusion barrier of 25–; however, the fusion barrier only becomes relevant when the SNAREpins are nearly completely zippered, and from this state, each SNAREpin can deliver only a small fraction of this energy as mechanical work. Therefore, they have to act cooperatively, and we show that at least three of them are needed to ensure fusion in less than a millisecond. However, to reach the prefusion state collectively, starting from the experimentally observed half-zippered metastable state, the SNAREpins have to mechanically synchronize, which takes more time as the number of SNAREpins increases. Incorporating this somewhat counterintuitive idea in a simple coarse-grained model results in the prediction that there should be an optimum number of SNAREpins for submillisecond fusion: three to six over a wide range of parameters. Interestingly, in situ cryoelectron microscope tomography has very recently shown that exactly six SNAREpins participate in the fusion of each synaptic vesicle. This number is in the range predicted by our theory.
Protein transport within cells relies heavily on membrane-enveloped vesicles that ferry packets of enclosed cargo (1–4). The content of the vesicles is released via their fusion with target membranes. This transition is impeded by repulsive forces acting when the distance between the membranes is in the range of . The encountered energy barrier is of the order of , implying that spontaneous fusion would take minutes, which is not fast enough in most biological situations (5–8). For this reason, the process is assisted by the assembly of SNARE proteins [soluble N-ethylmaleimide–sensitive factor attachment protein receptors (SNAREpins)], in which conformational change (zippering) exerts forces that pull the vesicle membrane toward the target membranes.
While the total free energy change associated with the zippering process is of the order of (9), most of this energy is consumed as the SNAREpins bring the membranes into close apposition. Biologically, the initial assembly before fusion provides compartmental specificity (pairing the correct SNAREs together) and allows for temporal regulation (clamping). Terminal zippering is then the process that uses the remaining energy for bilayer fusion at the small () separations where the repulsive forces become relevant. Recent studies suggest that each SNAREpin can deliver only about of mechanical work at this stage (10, 11), which explains why it takes about 1 s for a single SNAREpin to fuse two bilayers (12, 13).
It is known, however, that the release of neurotransmitters from synaptic vesicle occurring at nerve endings happens considerably faster, in a 10th of a millisecond as is necessary to keep pace with action potentials and ensure synchronous release (4, 14–18). A widely accepted explanation for this remarkable difference in timescales is that multiple SNAREpins would need to cooperate to accelerate fusion after being synchronously released from a clamped state. There have been indirect indications that the number of SNAREpins necessary to achieve a submillisecond fusion may be relatively small, ranging from two to six (19–21). Very recently, cryoelectron microscope tomography of synaptic vesicles in situ revealed an underlying sixfold symmetry, suggesting that exactly six SNAREpins are involved in such processes (22).
How so few co-operating SNAREpins manage to accelerate fusion 10,000 times (from to ) has been a complete mystery. Previous modeling attempts have suggested that more than 16 SNAREpins would be required (23, 24). Here, we show that the key to understanding how only a few SNAREpins can achieve such rapid fusion is the simple fact that they are mechanically coupled through effectively rigid common membranes. The account of such mechanical coupling leads to a striking prediction that the number of SNAREpins must be highly constrained to ensure submillisecond release of neurotransmitters. Quite remarkably, the predicted optimal range, three to six, is in excellent agreement with most recent experimental results (22).
We draw a fundamental analogy between the collective zippering of the SNAREpins and the power stroke in a bundle of elastically coupled muscle myosin II proteins, which is known to also take place at a 1-ms timescale. Building on the seminal theory of the myosin power stroke proposed by Huxley and Simmons (25), we model the fusion machinery as a mechanical system where the SNAREpins are represented as snap springs interacting through supporting membranes (26–28). The implied bistability is supported by recent experiments showing the presence of a metastable half-zipped state (10, 11).
The theoretical approach developed in this paper highlights the essential role of mechanical coupling among proteins undergoing conformational changes in ensuring swift, highly synchronized mechanical response. This is likely a general biological principle (27, 29).
Fusion Machinery
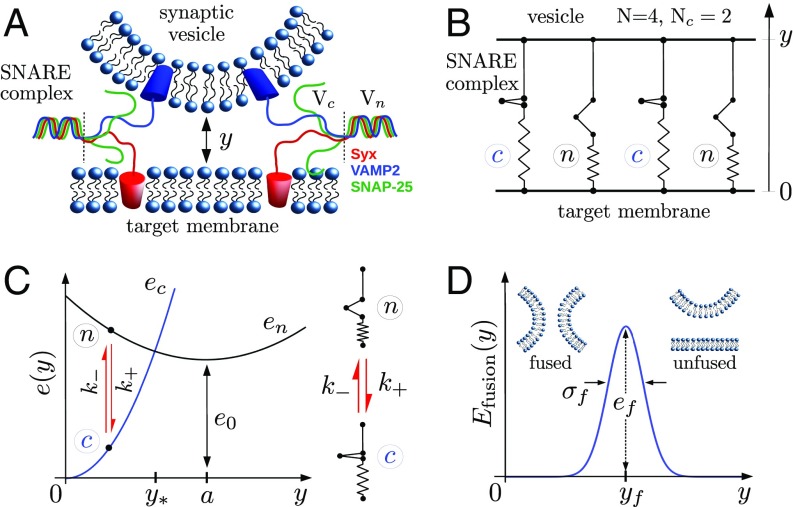
The goals of the model are to describe the dynamic coupling between the individual SNAREpins zippering and to study the associated evolution of the distance between the vesicle and the target membrane. The assembled SNARE machinery is represented as a bundle of parallel SNAREpins bridging the two membranes separated by the distance (Fig. 1 A and B). We assume that irreversible fusion occurs when this distance reaches a critical value . The characteristic length associated with the deformation of the membranes generated by a zippering SNAREpin is large compared with the typical size of the SNARE bundle (Rigid Membrane Assumption). Hence, the membranes can be viewed as two rigid backbones cross-linked by identically stretched SNAREpins.
Fig. 1.
The fusion machinery. (A) Schematic of the two membranes with two attached SNAREpins. (B) Mechanical model with SNAREpins in parallel bridging the two membranes separated by the distance . Two SNAREpins are in state , and two are in state ; therefore, . (C) Model of a single SNAREpin. (D) Fusion energy landscape. Table 1 has the complete list of parameter values.
Single SNAREpin as a Bistable Snap Spring.
The experimental work conducted in refs. 10, 11, and 30 suggests that a single SNAREpin can switch randomly between two metastable conformations: (half-zippered) when only the N-terminal domain of the SNAREs is zippered and (fully zippered) when both the C-terminal domain and the linker domain are zippered. To describe this process, we assume that the half-zippered to fully zippered transition in a SNARE complex is similar to the pre- to postpower stroke conformational change in a myosin motor (25, 27).
Suppose that each SNAREpin is equipped with an internal spin-type degree of freedom characterizing the state of the protein: or . We denote by the amount of shortening resulting from the transition in the absence of external load and by the energy difference between the two states. This parameter can be interpreted as the typical amount of mechanical work necessary to force the transition (partial unzipping) (Fig. 1C).
When the SNAREs are bound to the membranes, we assume that the rates —associated with the transition—and —associated with the transition—depend on the mechanical load induced by the variations of the intermembrane distance. To specify this dependence, both states are assumed to be “elastic” in the sense that they exist as phases over an extended range of separations due to elongations of the zippered and unzippered SNARE residues, internal bonds rearrangement, etc. (Fig. 1C). For simplicity, we assume that the deformations remain in the elastic regime so that states can be associated with quadratic energies , with minima located at and with the lumped stiffnesses . The transitions rates are defined so that, for a given separation, they favor the state with the lowest energy and verify detailed balance. Detailed expressions of and are in Model of a Single SNAREpin.
Dynamics of the Fusion Machinery.
The parallel arrangement of the SNAREs implies that the conformational state of the bundle is fully characterized by , the number of SNAREpins in state . This variable evolves according to the stochastic equation , with the outcomes , characterized by the probabilities , , and . While the SNAREpins can switch independently, the transition rates are functions of the collective variable with dynamics that in turn depends on .
To specify the coupling between the two degrees of freedom and and thereby, formulate the complete model of the fusion process, we first recall that the motion of the vesicle in the overdamped regime results from the balance between the force applied by the SNAREpins, the membrane repulsion, and the viscous drag. Taking into account the thermal fluctuations, this force balance translates into the stochastic equation
| [1] |
where is a standard white noise and is a drag coefficient representing the friction opposing the motion of the vesicle. At a given , the force applied by the bundle derives from the sum of individual SNAREpin energies . Finally, the intermembrane repulsion, due to short-range forces between the two membranes, is schematically modeled by a Gaussian energy barrier (5) , where is the critical separation and and are the height and width of the barrier, respectively (Fig. 1D). The ensuing dynamics of the system unfolds in the space of two stochastic variables: the continuous one, , and the integer-valued one, . The associated energy landscape has a multiwell structure that accounts for the configurational states of individuals. The response is governed by the two stochastic equations, for which initial conditions still need to be specified. We consider the initial state and , which corresponds to the configuration where the SNAREpins are at the bottom of the energy well describing state . This configuration characterizes the system immediately after the calcium-induced collapse of synaptotagmin, triggering the full zippering of the SNAREs (31). This point is discussed in more detail in Discussion.
Model Parameters.
The model is calibrated as follows (Table 1 and SI Appendix, section A have additional details). The mechanical parameters characterizing a single SNAREpin (, , , and ) are determined by using our model to reproduce the experimental results obtained from stretching tests with optical tweezers (9, 10). The energy bias and are chosen to be compatible with the results obtained from these studies. The procedure used to estimate the stiffnesses is more complex and explained in detail in SI Appendix. The value of the rate is fixed in accordance with estimates from refs. 10 and 34. The drag coefficient is computed using the Stokes formula , where is the vesicle radius and is the fluid viscosity. The corresponding characteristic timescale is .
Table 1.
Physical parameters adopted in the model and references
| Parameter | Symbol | Value | Units | Source |
| Zipping distance | 7 | nm | Ref. 10 | |
| Energy bias | 28 | Ref. 10 | ||
| Fully zipped stiffness | 12 | pN nm−1 | SI Appendix | |
| Half-zipped stiffness | 2.5 | pN nm−1 | SI Appendix | |
| Maximum zippering rate | 1 | MHz | Ref. 10 | |
| Drag coefficient | N s m−1 | |||
| FB position | 2 | nm | Refs. 5 and 32 | |
| FB width | 0.3 | nm | Refs. 6 and 33 | |
| FB height | 26 | Refs. 7 and 8 |
FB, fusion barrier. 1 kBT≈4 zJ.
The values of the parameters , , and are chosen to be compatible with the current literature (7, 8, 11, 12, 24, 23, 35–41). In particular, values of between 26 and have been reported for various types of lipids. We chose [POPC (1-palmitoyl-2-oleoyl-sn-glycero-3-phosphocholine) lipid] (8), which leads to a single SNAREpin average fusion time of 1 s.
Results
Numerical Simulations.
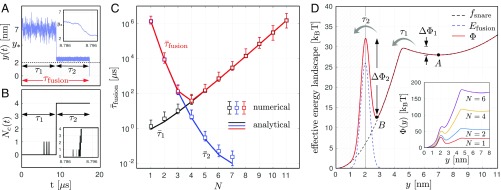
Typical stochastic trajectories and obtained from numerical simulations are shown in Fig. 2 A and B. They indicate that the fusion process can be decomposed into two stages characterized by the times and . During the first stage, the system remains in its initial configuration with only isolated transitions. After a time , the intermembrane distance drops abruptly to , while all of the SNAREpins collectively switch from state to state . Fig. 2 A, Inset and B, Inset show that this transition occurs within after the intermembrane distance has reached the value ; the irreversible collective zippering itself () lasts about . After the synchronized transition, the intermembrane distance remains above the threshold for a time before fusion. The duration of the whole process is, therefore, .
Fig. 2.
Main results. (A and B) Typical stochastic trajectories of the intermembranes distance (A) and the number of SNAREpins in state (B) obtained from the numerical simulation. The insets in A and B show magnification of the trajectories in the time interval (8.786 s, 8.796 s). (C) Average of the waiting times (black), (blue), and (red) obtained from the numerical simulations (symbols) and our effective chemical model (lines). (D) Effective free energy landscape showing the three stages of fusion and the associated transition rates. Parameters are listed in Table 1.
The mean timescales and (obtained by averaging 1,000 stochastic trajectories) are represented as functions of the number of SNAREpins in Fig. 2C on a semilogarithmic scale. Observe that increases exponentially with and decreases exponentially with . These antagonistic dependencies result in the average fusion time exhibiting a remarkably sharp minimum (Fig. 2C, red). With the set of parameters values reported in Table 1, this minimum is attained at and is associated with a fusion timescale of . In addition, we obtain a fusion time of the order of 1 s for a single SNAREpin. Both values are consistent with in vitro (12) and in vivo (14, 42) experimental measurements.
Fusion as a Two-Stage Reaction.
To elucidate the mechanism of fusion in two stages, we present here a “toy” model, where the whole process is recast as two successive reactions:
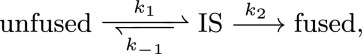 |
where IS stands for an intermediate state with characteristics that depend on the mechanical properties of the zippered SNAREpins. In this representation, the fusion is viewed as the outcome of two distinct substeps: the collective zippering and the topological membrane merger.
To justify such model reduction, we assume that the timescale of the transition is negligible compared with the timescale describing the relaxation of the vesicle position. In the corresponding limit (), Eq. 1 can be averaged with respect to the equilibrium distribution of the variable (Adiabatic Elimination of the Variable ), and therefore, the original system reduces to the one-dimensional stochastic equation:
| [3] |
where the energy appearing in Eq. 1—which depends on and —is replaced by the equilibrium free energy , which depends only on . This free energy is illustrated in Fig. 2D, dashed line. The overall potential driving the effective dynamics (3) is shown by the solid red line in Fig. 2D. It exhibits two local minima representing two metastable states. The first metastable state (point in Fig. 2D) is located at where, on average, all of the SNAREpins are in state . The second one (point in Fig. 2D) is located at and represents the intermediate state where, on average, all of the SNAREpins are in state , still confronting a reduced fusion barrier.
The system evolving in this energy landscape from the initial——to the final——state faces two successive energy barriers and . With each barrier , one can associate a waiting time that can be approximated by the Kramers formula (43–45):
| [4] |
The values of the numerical prefactors are determined by the local curvatures of the potential at its critical points and depend weakly on (Adiabatic Elimination of the Variable ).
The approximated timescales are compared with the numerically computed values in Fig. 2C, solid lines. The excellent agreement between the two sets of results suggests that the whole fusion process can effectively be described by two successive “chemomechanical” reactions and that the rates in Eq. 2 can be computed from the formulas , while the remaining rate is prescribed by the condition of detailed balance.
Finally, note that, with the parameters reported in Table 1, , which shows that our effective model is accurate even if the condition is not fully satisfied.
The peculiar dependencies of the waiting times on the number of SNAREpins can be now understood by referring to the dependence of the energy barriers .
Timescale : The cooperative action of the SNAREs reduces the time for crossing the fusion barrier.
In the intermediate state (point in Fig. 2D), the SNAREpins are all in state , and the pulling force that they apply on the membranes is exactly balanced by the short-range repulsive forces. The system remains trapped in this state until a thermal fluctuation provides the energy , allowing the system to reach the distance , where the fusion occurs.
In the absence of SNAREs, this energy difference is simply the bare fusion barrier (Fig. 1D). When the SNAREpins are present, the total force that they apply brings the two membranes in close contact, which reduces the energy barrier. This effect is amplified by an increase in the number of SNAREpins: the larger the number of SNAREpins, the larger the overall force, and therefore, the closer the membrane can be brought together (Fig. 2D).
Since the intermembrane potential decays rapidly as increases, we can approximate the second energy barrier by , where represents the amount of mechanical work that a single SNAREpin can deliver (Estimation of the Mechanical Work has the derivation of this result and the mathematical expression of ). According to Eq. 4, we then have
| [5] |
and hence, the exponential decay of the time with the number of SNAREpins.
With the parameters of Table 1, each SNAREpin provides a mechanical work when it encounters the fusion barrier, which reduces the average time for fusion by a factor of (Fig. 2D). This multiplicative effect allows fast fusion at the submillisecond timescale with as few as three SNAREpins. For a large-enough number of SNAREpins (here, ), the overall applied force surpasses the membrane repulsion, and the remaining fusion barrier disappears. The obtained exponential decay of the timescale with the number of SNAREpins suggests that the fusion could in principle proceed much faster than , being only limited by viscous forces. Considering that each vesicle can accommodate up to SNAREpins, one cannot rule out the possibility of neurotransmitter release occurring much faster than 100 s. Next, we suggest that this scenario is unlikely by showing that the fusion process gets slowed down if the number of SNAREpins becomes too large.
Timescale : Increasing the number of SNAREpins slows down the synchronous zippering.
The average time taken for all of the SNAREpins to switch from the to the conformation and then pull the membranes toward the bottom of the fusion barrier exponentially increases with the number of SNAREpins (Fig. 2C). This dependence can be explained as follows.
As long as , the individual transition rates are such that , which implies that, on average, all of the SNAREpins are in state and therefore, under compression (Fig. 1C). This idea is in agreement with the experimental results from ref. 9 that revealed the presence of the half-zipped metastable state. Consequently, in the interval , the average force, , collectively exerted by the SNAREpins on the membranes is repulsive. Beyond the point , the state is stabilized (), and the average force becomes attractive. Since this force is proportional to the number of SNAREpins, the waiting time before a fluctuation can provide enough energy to surpass the repulsion—and overcome the barrier —increases with . This constraint results from the mechanical feedback induced by the membranes. The membranes play the role of a rigid backbone that forces the SNAREpins to bridge approximately the same intermembrane distance (28, 29, 46).
To specify the dependence of , we use the fact that, for , we can consider that , and therefore, can be approximated by , where . According to Eq. 4, we can then write
| [6] |
which shows that the timescale increases exponentially with the number of SNAREpins.
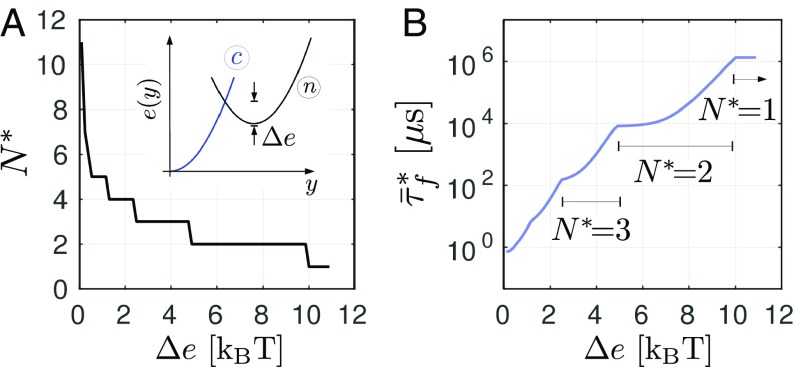
From Eq. 6, we obtained that the first energy barrier is fully controlled by a single parameter , which therefore, has a strong influence on both the existence and value of the optimal number of SNAREpins. To study the effect of on the fusion time, we varied the parameter describing the curvature of the energy . The results of our parametric study are summarized in Fig. 3. These data were obtained by using Eq. 4 to compute the intersection of the curves for each value of . We checked that the results are in good agreement with direct numerical simulations. Despite the broadness of the interval of parameter values tested, the optimal number of SNAREpins remains below 10. If we consider only the cases corresponding to submillisecond fusion times, we obtain with . The latter value is compatible with the recent estimate of for the transition energy barrier (9, 17). Note also that the predicted optimal number of SNAREpins is robust, because it corresponds to a plateau on the curve (Fig. 3A).
Fig. 3.
Effect of the intrinsic energy barrier on the optimal number of SNAREpins (A) and on the associated fusion time (B). The parameters values are taken from Table 1 with .
Robustness of the Predictions.
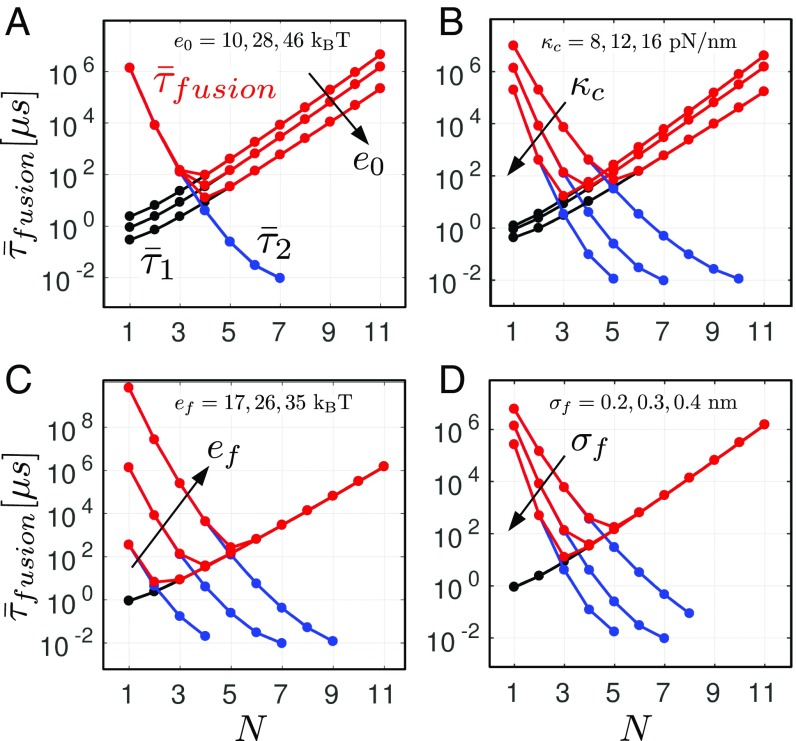
The results presented above were obtained for the parameter values listed in Table 1. For some of these parameters, only a rough estimate is available at this stage (SI Appendix). To test the robustness of our theoretical predictions, we computed the average waiting times from Eq. 4 for different values of four key parameters of the model: , , , and (Fig. 4). For each of these parameters, the lower bounds and the upper bounds delimit broad intervals covering the values obtained from different experimental studies.
Fig. 4.
Robustness of the prediction. Influence of the parameters (A), (B), (C), and (D) on the timescales and . The results were obtained using Eq. 4.
A comparison between Figs. 2B and 4 shows that our results are only marginally affected by changes in the parameter values. In particular, the existence of a sharp minimum of the fusion time associated with an optimal number of SNAREpins is a robust prediction. In addition, the value of the optimal number of SNAREpins is weakly sensitive to the parameters: it always remains in between three and six. Remarkably, despite the large difference between the upper and lower bounds for each of the parameters, the average fusion time remains in the submillisecond scale.
The energy landscape associated with the zippering of the SNARE complexes is the object of intense current research (9, 17, 47). In our model, this landscape is fully characterized by only four parameters: the distance , the energy , and the stiffnesses . While the distance has been measured with precision in recent works (9, 10), the values of the other three parameters are still not known with certainty. Several estimates of the energy bias lying between 20 and can been found in the literature (9, 48). We show in Fig. 4A that variations within this interval affect mostly and change the fusion time by one order of magnitude but have almost no effect on the optimal number of SNAREpins. Currently, only indirect evaluation of the stiffnesses can be obtained from the available data (SI Appendix). Within the broad range of values tested in our numerical simulations, we again observed only small variations of the optimal number of SNAREpins (Figs. 3 and 4B).
One of the most documented physical phenomena involved in the fusion process is the merging of the two membranes. The amplitude of the associated repulsion force depends in our model on the parameters and , the influence of which on the fusion time is illustrated in Fig. 4 C and D, respectively. As expected from the analysis presented in Results, changing the values of these two parameters affects only the height of energy barrier and therefore, the timescale . Increasing raises the height of the maximum of (Fig. 1D), while decreasing deepens the second energy well (point B in Fig. 2D), which results in both cases in the increase of . This leads in fine to the increase of the optimal number of SNAREs. Notice that depends on the type of lipids and on the membrane curvature and is also strongly sensitive to the membrane tension (37–41). Therefore, its value can be different in different cells or experimental setups. In particular, we expect the in vivo value to be smaller than the value measured in artificial systems (), which in general, use low-tension and low-curvature membranes (8).
In conclusion, while additional experimental studies are needed to refine the calibration of the model, the above parametric study shows the robustness of the effects of the mechanical cross-talk between the SNAREpins.
Discussion
In this paper, we have elucidated the central role played by mechanical coupling in synchronizing the activity of SNAREpins, which is necessary to enable submillisecond release of neurotransmitters. Our approach to the problem complements previous studies focused predominantly on the molecular details of the single SNARE zippering transition (9, 10, 30, 37, 47, 49–53).
As a starting point, we used a previously unnoticed analogy between the activity of SNARE complexes and the functioning of myosin II molecular motors. Viewed broadly, both systems ensure ultrafast mechanical contraction. In the case of muscle, destabilization of the prepower stroke state is the result of a mechanical bias created by an abrupt shortening of the myofibril (25, 54). In the case of SNAREs, similarly abrupt destabilization is a result of the calcium-induced removal of the synaptotagmin-based clamp, most likely when triggers disassembly of the synaptotagmin ring (55).
To pursue this analogy, we developed a variant of the power stroke model of Huxley and Simmons (25), in which the zipping is viewed as a transition between two discrete states endowed with different elastic properties (27). This representation is supported by recent experiments (9, 10), which provided essential data for the calibration of the model.
Our analysis of the collective behavior of “switchers” of this type suggests that the main function of the SNARE machinery is to bring the two membranes to a distance beyond which the fusion process can proceed spontaneously. The emerging intermediate configuration, where the two membranes are sufficiently closely tethered, can be then viewed as an intermediate state in the reaction process linking the fused and unfused states. The result is a representation of the SNARE-mediated fusion as a two-stage reaction.
We linked the first stage of the process with the collective zippering of the SNAREpins and showed that this step gets exponentially more sluggish as the number of SNAREpins increases. This phenomenon was studied previously in the context of muscles (26, 29). It originates (i) from the experimentally suggested presence of a metastable half-zipped state along the zippering free energy landscape (9) and (ii) from the long-range mechanical interactions mediated by the scaffolding membranes, which create a negative feedback that prevents a fast collective escape from the metastable half-zippered state.
The second stage of the process is the transition from the intermediate state to the fused state. The associated timescale decreases exponentially with the number of SNAREpins, because the larger the number of acting SNAREpins the closer the membranes can be brought together in the intermediate state and therefore, the higher the energy of this state. This results in an exponential decay of the timescale with the number of SNAREpins. Behind this phenomenon is the presence of a residual force in the configuration where the SNAREpins have reached the intermediate state. This perspective is supported by the results of refs. 10 and 11.
The antagonistic dependence of the rates characterizing the two stages reveals the existence of an optimal number of SNAREs that allows the system to perform fusion at the physiologically appropriate timescales. Our prediction is supported by recent in situ cryoelectron microscope tomography observation, see ref. 22.
We remark that our results strongly depend on the initial configuration of the system, which we link with the structure of the fusion machinery immediately after synaptotagmin removal by calcium. Notice that the position of the barrier separating the half-zippered and fully zippered states is such that . Therefore, the timescale exists only if the initial membrane separation . This assumption seems to be supported by experiments (56). It has previously been reported that, on approach of two membranes devoid of SNAREs, synaptotagmin exerts repulsive force from down to , where it becomes a repulsive wall (56). According to this result, should range between 4 and . However, it is probably slightly larger under physiological conditions because of the presence of the SNAREs. With the parameters adopted in our simulations (Table 1), the position of the barrier is in accordance with refs. 9 and 10 (Fig. 2). Therefore, in all likelihood, is larger than , and our predictions should be valid.
Finally, we mention, the fact that the timescale exponentially decreases with seems to be supported by experimental studies reporting submillisecond fusion time with (19–21). However, in a recent theoretical study, the decay was also found to be exponential but with a much slower decay: the cooperation of at least 16 SNAREs was predicted to be necessary to reach the physiological fusion time (23, 24). The difference is explained by the fact that the residual work in this study is instead of in our model (Eq. 5). This difference originates from the assumption made by the authors that the zippering energy of the SNARE complex is entirely dissipated before the membranes encounter the fusion barrier. In other words, the authors have implicitly assumed that, after the calcium entry, the zippering of the SNAREpins does not generate any pulling force to assist fusion and concluded that the remaining residual force is of entropic nature. Recent direct microscopic observations implying that synaptic fusion involves only six SNAREpins (22) would seem to invalidate this assumption.
In conclusion, our model describes membrane fusion by a team of mechanically interacting SNAREpins as a two-stage process. We show that conventional biochemical and biophysical measurements cannot be used directly to predict the associated rates and that mechanical modeling is crucial for linking these rates with independently measured parameters. Our work emphasizes the importance of identifying mechanical pathways and specifying mechanistic feedbacks. The main conceptual outcome of our study is the realization that, in the case of synaptic fusion, SNARE proteins can perform optimally only if they act collectively. The remarkable fact is that, when the team is of the optimal size, such synchronization is not deterred by thermal fluctuations, which guarantees that the collective strike is simultaneously fast, strong, and robust.
Finally, we mention that the synaptic fusion is only one of many biophysical processes involving mechanically induced collective conformational changes. Other examples include ion gating in hair cells (57, 58), collective decohesion of adhesive clusters (59, 60), folding–unfolding of macromolecular hairpins (61–63), and folding of ParB–ParS complexes in DNA condensation (64, 65). In each of these situations, one can identify a dominating long-range mechanical interaction, making the theoretical framework developed in this paper potentially useful.
Materials and Methods
Rigid Membrane Assumption.
We assume for simplicity that the vesicle and the target membranes are rigid, which implies that all of the SNAREpins share the same intermembrane distance . This approximation is valid if the characteristic length associated with the deformation generated by a single SNAREpin is large compared with the size of the SNARE bundle. We can use the following estimate , where is the membrane rigidity and is the membrane tension. We have typically and ; therefore, . Since the size of the SNARE bundle is less than , our assumption should be valid.
Model of a Single SNAREpin.
We set, for simplicity, that the energies and of the SNAREpins in the states and , respectively, depend on quadratically, so that
| [7] |
where represent lumped stiffnesses parameters. We denote as the distance where (Fig. 1C). In the absence of external load (zero force), the stable states are located at and . In this situation, the entire energy associated with the zippering process is consumed when the SNAREpin reaches state at , which can then be considered as a ground state with zero energy.
The rates of the transitions obey the detailed balance relation , with the bias toward the direct transition (i.e., ) at and conversely, in the direction of the reverse transition at (Fig. 1C).
For simplicity and following ref. 25, we consider that the transition from the high-energy state to the low-energy state occurs at a constant rate , which fixes the characteristic timescale of the conformational change. This assumption could be easily replaced by a more adequate one at the expense of introducing two additional parameters, but with only a minimal impact on the results (28). With this assumption and using the detailed balance, we write the transition rates as
Numerical Implementation of the Model.
The discrete stochastic process associated with the variable was simulated as a two-state Markov chain with a fixed timestep . At each timestep, the transition probabilities are computed, and the next event is chosen based on an acceptation–rejection condition using a random number uniformly distributed between 0 and 1. The Langevin equation was simulated using a first-order explicit Euler scheme. More details about the computer algorithms can be found in SI Appendix.
Adiabatic Elimination of the Variable .
We consider the situation where : the characteristic time of the conformational changes is negligible compared with the timescale associated with the relaxation of the vesicle’s position. In this limit, the conformational state of each SNAREpin can be considered at equilibrium. Therefore, for a given position of the vesicle , the probability of a configuration with SNAREpins in state follows the Boltzmann distribution
| [8] |
where . We then integrate Eq. 1 with respect to the distribution (8) and obtain Eq. 3. Since the energy is linear in , our approximation results in replacing with its average in Eq. 1. In Eq. 4, the prefactors are given by: , where and denote the positions of the considered barrier and minimum, respectively (see ref. 45).
Estimation of the Mechanical Work .
In the intermediate state, intermembrane distance is sufficiently lower than the threshold so that the free energy can be well approximated by the energy of the state . We then write , which leads to the following expression for the energy barrier separating the intermediate state and the fused state:
By noting that verifies , we obtain with
Notice that, since the energy decays rapidly for , the parameter depends weakly on .
Supplementary Material
Acknowledgments
We thank Yongli Zhang for providing us with the data used for the calibration of our model and Ben O’Shaughnessy for stimulating discussions. This work was supported by European Research Council-funded Grant 669612 (to J.E.R.) under the European UnionQs Horizon 2020 Research and Innovation Program.
Footnotes
The authors declare no conflict of interest.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1820394116/-/DCSupplemental.
References
- 1.Ivanov AI. Exocytosis and Endocytosis. Vol 440. Humana; Totowa, NJ: 2008. [DOI] [PubMed] [Google Scholar]
- 2.Vassilieva EV, Nusrat A. 2008. Vesicular trafficking: Molecular tools and targets. Exocytosis and Endocytosis, Methods in Molecular Biology, ed Ivanov AI (Humana, New York), Vol 440, pp 3–14.
- 3.Jahn R, Fasshauer D. Molecular machines governing exocytosis of synaptic vesicles. Nature. 2012;490:201–207. doi: 10.1038/nature11320. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Südhof TC, Rothman JE. Membrane fusion: Grappling with SNARE and SM proteins. Science. 2009;323:474–477. doi: 10.1126/science.1161748. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Rand RP, Parsegian VA. Hydration forces between phospholipid bilayers. Biochim Biophys Acta Rev Biomembr. 1989;988:351–376. [Google Scholar]
- 6.Leckband D, Jacob I. Intermolecular forces in biology. Q Rev Biophys. 2001;34:105–267. doi: 10.1017/s0033583501003687. [DOI] [PubMed] [Google Scholar]
- 7.Ryham R, Klotz TS, Yao L, Cohen FS. Calculating transition energy barriers and characterizing activation states for steps of fusion. Biophys J. 2016;110:1110–1124. doi: 10.1016/j.bpj.2016.01.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.François-Martin C, Rothman JE, Pincet F. Low energy cost for optimal speed and control of membrane fusion. Proc Natl Acad Sci USA. 2017;114:1238–1241. doi: 10.1073/pnas.1621309114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Zhang Y. Energetics, kinetics, and pathway of SNARE folding and assembly revealed by optical tweezers. Protein Sci. 2017;26:1252–1265. doi: 10.1002/pro.3116. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Gao Y, et al. Single reconstituted neuronal SNARE complexes zipper in three distinct stages. Science. 2012;337:1340–1343. doi: 10.1126/science.1224492. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Zhang Z, Jackson MB. Temperature dependence of fusion kinetics and fusion pores in Ca 2+-triggered exocytosis from PC12 cells. J Gen Physiol. 2008;131:117–124. doi: 10.1085/jgp.200709891. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Xu W, et al. A programmable DNA origami platform to organize SNAREs for membrane fusion. J Am Chem Soc. 2016;138:4439–4447. doi: 10.1021/jacs.5b13107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Domanska MK, Kiessling V, Stein A, Fasshauer D, Tamm LK. Single vesicle millisecond fusion kinetics reveals number of SNARE complexes optimal for fast SNARE-mediated membrane fusion. J Biol Chem. 2009;284:32158–32166. doi: 10.1074/jbc.M109.047381. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Südhof TC. The synaptic vesicle cycle. Annu Rev Neurosci. 2004;27:509–547. doi: 10.1146/annurev.neuro.26.041002.131412. [DOI] [PubMed] [Google Scholar]
- 15.Camacho M, et al. Heterodimerization of Munc13 C2A domain with RIM regulates synaptic vesicle docking and priming. Nat Commun. 2017;8:15293. doi: 10.1038/ncomms15293. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Liu X, et al. Functional synergy between the Munc13 C-terminal C1 and C2 domains. Elife. 2016;5:965. doi: 10.7554/eLife.13696. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Li F, Tiwari N, Rothman JE. Kinetic barriers to SNAREpin assembly in the regulation of membrane docking/priming and fusion. Proc Natl Acad Sci USA. 2016;113:10536–10541. doi: 10.1073/pnas.1604000113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Shyam SK, et al. Re-visiting the trans insertion model for complexin clamping. Elife. 2015;4:1021. doi: 10.7554/eLife.04463. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Hua Y, Scheller RH. Three SNARE complexes cooperate to mediate membrane fusion. Proc Natl Acad Sci USA. 2001;98:8065–8070. doi: 10.1073/pnas.131214798. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Sinha R, Ahmed S, Jahn R, Klingauf J. Two synaptobrevin molecules are sufficient for vesicle fusion in central nervous system synapses. Proc Natl Acad Sci USA. 2011;108:14318–14323. doi: 10.1073/pnas.1101818108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Mohrmann R, de Wit H, Verhage M, Neher E, Sørensen JB. Fast vesicle fusion in living cells requires at least three SNARE complexes. Science. 2010;330:502–505. doi: 10.1126/science.1193134. [DOI] [PubMed] [Google Scholar]
- 22.Li X, et al. Symmetrical organization of proteins under docked synaptic-vesicles. FEBS Lett. December 18, 2018 doi: 10.1002/1873-3468.13316. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Mostafavi H, et al. Entropic forces drive self-organization and membrane fusion by SNARE proteins. Proc Nat Acad Sci USA. 2017;114:5455–5460. doi: 10.1073/pnas.1611506114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.McDargh ZA, Polley A, O’Shaughnessy B. SNARE-mediated membrane fusion is a two-stage process driven by entropic forces. FEBS Lett. 2018;592:3504–3515. doi: 10.1002/1873-3468.13277. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Huxley AF, Simmons RM. Proposed mechanism of force generation in striated muscle. Nature. 1971;233:533–538. doi: 10.1038/233533a0. [DOI] [PubMed] [Google Scholar]
- 26.Caruel M, Allain J-M, Lev T, Lev T. Muscle as a metamaterial operating near a critical point. Phys Rev Lett. 2013;110:248103. doi: 10.1103/PhysRevLett.110.248103. [DOI] [PubMed] [Google Scholar]
- 27.Caruel M, Lev T. Statistical mechanics of the Huxley-Simmons model. Phys Rev E. 2016;93:062407. doi: 10.1103/PhysRevE.93.062407. [DOI] [PubMed] [Google Scholar]
- 28.Caruel M, Lev T. Bi-stability resistant to fluctuations. J Mech Phys Sol. 2017;109:117–141. [Google Scholar]
- 29.Caruel M, Lev T. Physics of muscle contraction. Rep Prog Phys. 2018;81:036602. doi: 10.1088/1361-6633/aa7b9e. [DOI] [PubMed] [Google Scholar]
- 30.Sutton RB, Fasshauer D, Jahn R, Brunger AT. Crystal structure of a SNARE complex involved in synaptic exocytosis at 2.4Åresolution. Nature. 1998;395:347–353. doi: 10.1038/26412. [DOI] [PubMed] [Google Scholar]
- 31.Südhof TC. Neurotransmitter release: The last millisecond in the life of a synaptic vesicle. Neuron. 2013;80:675–690. doi: 10.1016/j.neuron.2013.10.022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Evans E. Entropy-driven tension in vesicle membranes and unbinding of adherent vesicles. Langmuir. 1991;7:1900–1908. [Google Scholar]
- 33.Donaldson SH, Lee CT, Chmelka BF, Israelachvili JN. General hydrophobic interaction potential for surfactant/lipid bilayers from direct force measurements between light-modulated bilayers. Proc Natl Acad Sci USA. 2011;108:15699–15704. doi: 10.1073/pnas.1112411108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Yang WY, Gruebele M. Folding at the speed limit. Nature. 2003;423:193–197. doi: 10.1038/nature01609. [DOI] [PubMed] [Google Scholar]
- 35.Lentz BR, Lee J. Poly(ethylene glycol) (PEG)-mediated fusion between pure lipid bilayers: A mechanism in common with viral fusion and secretory vesicle release? (Review) Mol Membr Biol. 2009;16:279–296. doi: 10.1080/096876899294508. [DOI] [PubMed] [Google Scholar]
- 36.Cohen FS, Melikyan GB. The energetics of membrane fusion from binding, through hemifusion, pore formation, and pore enlargement. J Membr Biol. 2004;199:1–14. doi: 10.1007/s00232-004-0669-8. [DOI] [PubMed] [Google Scholar]
- 37.Markvoort AJ, Marrink SJ. Lipid acrobatics in the membrane fusion arena. Curr Top Membr. 2011;68:259–294. doi: 10.1016/B978-0-12-385891-7.00011-8. [DOI] [PubMed] [Google Scholar]
- 38.Finkelstein A, Zimmerberg J, Cohen FS. Osmotic swelling of vesicles: Its role in the fusion of vesicles with planar phospholipid bilayer membranes and its possible role in exocytosis. Annu Rev Physiol. 1986;48:163–174. doi: 10.1146/annurev.ph.48.030186.001115. [DOI] [PubMed] [Google Scholar]
- 39.Grafmüller A, Shillcock J, Lipowsky R. Pathway of membrane fusion with two tension-dependent energy barriers. Phys Rev Lett. 2007;98:218101. doi: 10.1103/PhysRevLett.98.218101. [DOI] [PubMed] [Google Scholar]
- 40.Grafmüller A, Shillcock J, Lipowsky R. The fusion of membranes and vesicles: Pathway and energy barriers from dissipative particle dynamics. Biophys J. 2009;96:2658–2675. doi: 10.1016/j.bpj.2008.11.073. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Lee JY, Schick M. Calculation of free energy barriers to the fusion of small vesicles. Biophys J. 2009;94:1699–1706. doi: 10.1529/biophysj.107.119511. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Meinrenken CJ, Borst JGG, Sakmann B. Calcium secretion coupling at calyx of held governed by nonuniform channel–vesicle topography. J Neurosci. 2002;22:1648–1667. doi: 10.1523/JNEUROSCI.22-05-01648.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.HA K. Brownian motion in a field of force and the diffusion model of chemical reactions. Physica. 1940;7:284–304. [Google Scholar]
- 44.Risken H. The Fokker-Planck Equation Methods of Solution and Application. Springer; Berlin: 1988. [Google Scholar]
- 45.Schuss Z. Theory and Application of Stochastic Processes: An Analytical Approach. Vol 170 Springer; New York: 2010. [Google Scholar]
- 46.Caruel M, Allain J-M, Lev T. Mechanics of collective unfolding. J Mech Phys Sol. 2015;76:237–259. [Google Scholar]
- 47.Walter AM, Wiederhold K, Bruns D, Fasshauer D, Sørensen JB. Synaptobrevin N-terminally bound to syntaxin–SNAP-25 defines the primed vesicle state in regulated exocytosis. J Cell Biol. 2010;188:401–413. doi: 10.1083/jcb.200907018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Li F, et al. Energetics and dynamics of SNAREpin folding across lipid bilayers. Nat Struct Mol Biol. 2007;14:890–896. doi: 10.1038/nsmb1310. [DOI] [PubMed] [Google Scholar]
- 49.Risselada HJ, Grubmüller H. How snare molecules mediate membrane fusion: Recent insights from molecular simulations. Curr Opin Struct Biol. 2012;22:187–196. doi: 10.1016/j.sbi.2012.01.007. [DOI] [PubMed] [Google Scholar]
- 50.Acuna C, et al. Microsecond dissection of neurotransmitter release: SNARE-complex assembly dictates speed and Ca2 sensitivity. Neuron. 2014;82:1088–1100. doi: 10.1016/j.neuron.2014.04.020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Hernandez JM, et al. Membrane fusion intermediates via directional and full assembly of the SNARE complex. Science. 2012;336:1581–1584. doi: 10.1126/science.1221976. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Li F, et al. A half-zippered SNARE complex represents a functional intermediate in membrane fusion. J Am Chem Soc. 2014;136:3456–3464. doi: 10.1021/ja410690m. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Stein A, Weber G, Wahl MC, Jahn R. Helical extension of the neuronal SNARE complex into the membrane. Nature. 2009;460:525–528. doi: 10.1038/nature08156. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Ford LE, Ford LE, Huxley AF, Simmons RM. Tension responses to sudden length change in stimulated frog muscle fibres near slack length. J Physiol. July 1977;269:441–515. doi: 10.1113/jphysiol.1977.sp011911. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Ramakrishnan S, et al. Synaptotagmin oligomers are necessary and can be sufficient to form a Ca2+-stable fusion clamp. FEBS Lett. December 20, 2018 doi: 10.1002/18733468.13317. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Gruget C, et al. Rearrangements under confinement lead to increased binding energy of Synaptotagmin-1 with anionic membranes in Mg 2+and Ca 2+ FEBS Lett. 2018;592:1497–1506. doi: 10.1002/1873-3468.13040. [DOI] [PubMed] [Google Scholar]
- 57.Martin P, Martin P, Mehta A, Hudspeth A. Negative hair-bundle stiffness betrays a mechanism for mechanical amplification by the hair cell. Proc Natl Acad Sci USA. 2000;97:12026–12031. doi: 10.1073/pnas.210389497. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Bormuth V, Barral J, Joanny JF, Jülicher F, Martin P. Transduction channels’ gating can control friction on vibrating hair-cell bundles in the ear. Proc Natl Acad Sci USA. 2014;111:7185–7190. doi: 10.1073/pnas.1402556111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Yao HM, Gao HJ. Mechanics of robust and releasable adhesion in biology: Bottom–up designed hierarchical structures of gecko. J Mech Phys Sol. 2006;54:1120–1146. [Google Scholar]
- 60.Erdmann T, Schwarz US. Impact of receptor-ligand distance on adhesion cluster stability. Eur Phys J. 2007;22:123–137. doi: 10.1140/epje/e2007-00019-8. [DOI] [PubMed] [Google Scholar]
- 61.Woodside MT, Garcia-Garcia C, Block SM. Folding and unfolding single RNA molecules under tension. Curr Opin Chem Biol. 2008;12:640–646. doi: 10.1016/j.cbpa.2008.08.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Bosaeus N, et al. Tension induces a base-paired overstretched dna conformation. Proc Natl Acad Sci USA. 2012;109:15179–15184. doi: 10.1073/pnas.1213172109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Liphardt J, Onoa B, Smith SB, Tinoco I, Bustamante C. Reversible unfolding of single rna molecules by mechanical force. Science. 2001;292:733–737. doi: 10.1126/science.1058498. [DOI] [PubMed] [Google Scholar]
- 64.Chen B-W, Lin M-H, Chu C-H, Hsu C-E, Sun Y-J. Insights into ParB spreading from the complex structure of Spo0J and parS. Proc Natl Acad Sci USA. 2015;112:6613–6618. doi: 10.1073/pnas.1421927112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Funnell BE. ParB partition proteins: Complex formation and spreading at bacterial and plasmid centromeres. Front Mol Biosci. 2016;3:44. doi: 10.3389/fmolb.2016.00044. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.