Abstract
We describe recent technological progress in multimodal en face full-field optical coherence tomography that has allowed detection of slow and fast dynamic processes in the eye. We show that by combining static, dynamic and fluorescence contrasts we can achieve label-free high-resolution imaging of the retina and anterior eye with temporal resolution from milliseconds to several hours, allowing us to probe biological activity at subcellular scales inside 3D bulk tissue. Our setups combine high lateral resolution over a large field of view with acquisition at several hundreds of frames per second which make it a promising tool for clinical applications and biomedical studies. Its contactless and non-destructive nature is shown to be effective for both following in vitro sample evolution over long periods of time and for imaging of the human eye in vivo.
1. Introduction
Optical coherence tomography (OCT) is used in the biomedical field to image microstructures in tissue using mostly the endogenous backscattering contrast [1,2]. Full-field optical coherence tomography (FFOCT) is an en face, high transverse resolution version of OCT [3, 4]. Using incoherent light sources, two-dimensional detectors and a time-domain phase stepping scheme, FFOCT acquires en face oriented virtual sections of the sample at a given depth and has been used for biology [5], and medicine [6]. Recently, new multimodal techniques, based either on OCT or FFOCT, have enabled the study not only of the static 3D morphology of a sample but also of the dynamics of its scatterers [7,8] by measuring phase-sensitive temporal fluctuations of the backscattered light. In ex-vivo fresh unfixed tissues, these dynamic techniques reveal subcellular structures that are very weak backscatterers and provide additional contrast based on their intracellular motility [9,10]. FFOCT multimodal techniques can also detect collective subcellular motion of scatterers resulting from either static deformations or propagating elastic waves for mapping elastic properties or flow of cells in capillaries [11, 12]. Complementary contrast from dynamic and static properties coupled in a multimodal setup with high resolution FFOCT thus enables noninvasive visualization of biological tissue, microstructural, morphological and dynamic properties at the cellular level without the use of exogenous markers. Nevertheless, in order to achieve identification of specific molecular structures, OCT images often need to be compared with fluorescence images or stained histology slides to understand and identify the observed microstructures. Indeed, fluorescence microscopy reveals molecular contrast using dyes or genetically encoded proteins that can be attached to a specific structure of interest and/or monitor changes of the biochemical properties of the tissue. Structured illumination microscopy (SIM) [13–15], a full-field version of confocal microscopy, can perform micrometer scale optical sections in a tissue and has been coupled to static and dynamic FFOCT (D-FFOCT) [16,17] to allow simultaneous coincident multimodal fluorescence and FFOCT acquisitions.
OCT and FFOCT are often used in tissue to overcome the difficulties linked to scattering induced by small scale refractive index discontinuities, but large-scale discontinuities are also present and induce aberrations that could affect the resolution [18]. Recently, we have demonstrated that low order geometrical aberrations do not affect the point spread function (PSF) but mostly reduce the signal to noise ratio (SNR) when using interferometry with a spatially incoherent source [18,19]. This allows us to achieve resolution of cone photoreceptors in vivo in the human retina without adaptive optics [19].
In vivo imaging, and detection of in vitro subcellular dynamics, would not have been possible using FFOCT without recent technological advances in detector technology that we will evaluate for static and dynamic FFOCT cases. Although we have developed different multimodal FFOCT-based biomedical imaging applications in oncology [20], embryology, cardiology and ophthalmology [21–23], we will restrict the field of the present paper to new results obtained in ophthalmology. We will discuss the technical issues of sample immobilization for in vitro and ex vivo imaging, along with processing methods that were applied for the first time in FFOCT leading to the first dynamic 3D reconstruction with sub-micron resolution of a macaque retinal explant. An axial sub-micron plane locking procedure is presented to image the same sample plane over several hours in a time-lapse fashion, and applied to image slow wound healing on a macaque cornea. Quantitative methods derived from computer vision were adapted to produce a cell migration map with micrometer resolution. We also introduce a combined posterior/anterior eye imaging setup which in addition to traditional FFOCT imaging offers the possibility to measure the blood flow in the anterior eye that compares favorably to existing techniques [24–26]. Finally, an approach that combines fluorescence labeling for live cells with static and dynamic FFOCT is presented.
2. Methods
Although the principle of OCT is mature and well established, it is still an active area of research where improvements mainly rely on hardware performance. In the case of FFOCT, the camera performance is critical to achieve sufficient single shot sensitivity for imaging 3D biological samples with low reflectivity such as cornea and retina in depth. Recently, a new sensor with an improved full well capacity (FWC) combined with faster electronics allowed faster acquisition with better SNR. The gain in speed is of critical importance when it comes to imaging moving samples, whereas the improvement in SNR is particularly important to image weakly reflective samples in-depth. With the recent development of D-FFOCT, the need for a high FWC camera is even greater as the dynamic fluctuations probed are weaker than the static signals, due to the small size of the moving scatterers. Also the setup stability needs to be studied to ensure that the measured dynamics are in the sample and are not caused by artifactual mechanical vibrations.
2.1. Signal to noise ratio in FFOCT
Two FFOCT modalities were used throughout this work - static images were acquired using a two phase scheme and dynamic images are processed using a stack of direct images - and in both cases the camera is used close to saturation in order to use the whole FWC. For a two phase acquisition, two frames are recorded with a π-shift phase difference. The intensity recorded on a camera pixel is the coherent sum of the reference and sample beams (which contains coherent and incoherent terms) and can be written:
| (1) |
| (2) |
where IΦ=0 is the intensity recorded without phase shift, IΦ=π is the intensity recorded for a π phase shift, η is the camera quantum efficiency, I0 is the power LED output (we considered a 50/50 beam-splitter), α is the reference mirror reflectivity (i.e. the power reflection coefficient), R is the sample reflectivity (i.e. the power reflection coefficient), Δϕ is the phase difference between the reference and sample back-scattered signals, Iincoh = RincohI0/4 is the incoherent light back-scattered by the sample on the camera, mainly due to multiple scattering and specular reflection on the sample surface. The static image is formed by subtracting IΦ=π from IΦ=0 and taking the modulus:
| (3) |
For a 2-phase scheme it is not possible to un-mix amplitude and phase. To get rid of the cosine term we consider that the phase is uniformly distributed (both in time and space) in biological samples and we can average I2–phase with respect to the phase distribution:
| (4) |
Returning to the recorded intensity IΦ, the terms related to sample arm reflectivity are negligible compared to the incoherent and reference terms so the intensity corresponding to pixel saturation Isat can be written:
| (5) |
Combining Eq. (4) and Eq. (5) we obtain:
| (6) |
If we consider an ideal case when the experiment is shot noise limited, the noise is proportional to , which gives the following signal to noise ratio:
| (7) |
The SNR is proportional to and is therefore proportional to the maximal number of photoelectrons that a pixel can generate before saturation, which is the definition of the FWC. Thus the SNR is proportional to the FWC for a 2-phase FFOCT image. D-FFOCT images are computed by taking the temporal standard deviation of the signal, see Section 2.4. We consider that both the local reflectivity and phase can fluctuate. The noise term remains the same, as we also work close to saturation during dynamic acquisitions. The measured intensity can then be written:
| (8) |
| (9) |
Where SD is the standard deviation operator. The dynamic SNR can therefore be written:
| (10) |
Equation (10) shows that the camera FWC also limits the SNR in D-FFOCT experiments. One can argue that averaging several FFOCT images could be a workaround for 2-phase images. Considering the case of a weakly reflective sample (e.g. cornea and retina) and a moving sample (e.g. the eye) then one needs to have sufficient signal to perform registration before averaging, therefore SNR on single frames is of great importance and thus all experiments are conducted with the camera working close to saturation.
2.2. Improving signal to noise ratio and speed
The most widely used camera for FFOCT (MV-D1024E-160-CL-12, PhotonFocus, Switzerland) has a 2 × 105 electrons FWC with a maximum framerate of 150 frame.s−1 at 1024 × 1024 pixels. With α = 0.08 (as we typically use 4% to 18% reflectivity mirrors) it leads to a 70 dB sensitivity for a 2-phase image reconstruction with 75 processed images.s−1. Averaging 100 images with this camera takes just over 1 second and leads to a 90 dB sensitivity. A major recent change in our setups has been the introduction of a new camera, specifically designed for FFOCT requirements (Quartz 2A750, ADIMEC, Netherlands) that has a maximum framerate of 720 frame.s−1 at 1440 × 1440 pixels and a 2 × 106 FWC. With the new camera characteristics, it is possible to achieve 83 dB sensitivity for a 2-phase image reconstruction. Acquiring and averaging 100 images takes under 0.2 second and leads to 103 dB sensitivity. This result brings the SNR of FFOCT and the speed per voxel in en-face views up to the typical range of conventional OCT systems, but with a better transverse resolution given by the NA of the objective. Aside from SNR improvement, the second major advantage of this new camera is its acquisition speed. Speed is an important issue for detection of in vitro subcellular dynamics, and crucial to in vivo eye examination. Indeed, in contrast to scanning OCT setups, FFOCT requires the acquisition of a full megapixel image in a single shot, and the signal can be lost if a lateral displacement occurs between two successive images. This typically imposes a minimum acquisition speed higher than 200 frames.s−1 as eye motions are mainly below 100 Hz [27,28], a condition that is easily met by the new camera which offers 720 frames.s−1.
2.3. Improving sample stability
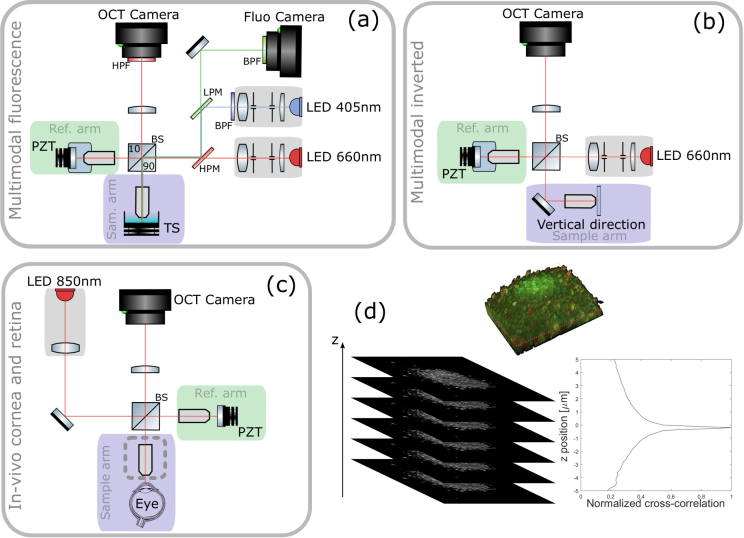
Previously described in vitro imaging setups [10,16] were mounted vertically with the sample placed under the objective and imaged from above, see Fig. 1(a). This setup consists of a Linnik interferometer with an excitation source (M405L3, Thorlabs) for fluorescence imaging and an FFOCT source (M660L3, Thorlabs). Illumination paths are combined and separated using dichroic filters. Both sample and reference arms are mounted on translation stages (X-NA08A25, Zaber Technologies). In addition, the reference mirror is mounted on a piezoelectric translation stage (STr-25, Piezomechanik) for phase-shifting. In this configuration, in order to image fresh ex-vivo samples in immersion, we had to fix them in place using a 3D printed mounting system with transparent membrane covering and gently restraining the sample in order to prevent any movement during imaging. To facilitate imaging of cell cultures that are directly adhered to the base of a dish, and to use gravity to assist immobilization for other tissue samples, we have built a new system in an inverted configuration where the sample is directly placed on a coverslip and imaged from beneath with high-numerical-aperture oil-immersed objectives, see Fig. 1(b). This setup is mounted with the same parts as the previous one, except that it does not feature fluorescence measurement capabilities and is mounted horizontally, with the sample arm mounted vertically. The main advantage is that the sample is held motionless by gravity and is naturally as flattened as possible (thus providing a flat imaging plane) against the coverslip surface without applying compression. Despite these efforts to immobilize the sample, axial drift on the micrometer scale over long periods of time can occur in either configuration. In order to compensate for the axial drift we introduced an automated plane locking procedure based on static FFOCT image correlation around the current position, see Fig. 1(d). FFOCT images are acquired over an axial extent of 10 μm, taking 0.5 μm steps with the sample translation stage, and are then cross-correlated with the target image. The sample is then axially translated to the position corresponding to the maximum of the cross-correlation, which was typically between 0.5–0.8. After each plane correction procedure, a new FFOCT image is taken as target for the next correction in order to account for evolution in the sample position. This procedure was performed every 10 minutes. We observed that for long acquisitions of several hours, the time between autofocus procedures could be increased as we reached a quasi-equilibrium state. Using this procedure we are able to image the same plane in biological samples over a day. The in vivo imaging was performed according to procedures already described in [23] which essentially acquire images in a plane chosen by visual inspection of the live image, and did not include active plane locking.
Fig. 1.
PZT: piezoelectric translation - TS: translation stage - LPM: low pass dichroic filter - HPM: high pass dichroic filter - (a) Multimodal static and dynamic FFOCT combined with fluorescence side view. The camera used for FFOCT in all setups is an ADIMEC Quartz 2A750. The camera used for fluorescence is a PCO Edge 5.5. Microscope objectives are Nikon NIR APO 40× 0.8 NA. (b) Multimodal static and dynamic FFOCT inverted system top view. Microscope objectives are Olympus UPlanSApo 30× 1.05 NA. (c) In vivo FFOCT setup for anterior eye imaging (with Olympus 10× 0.3 NA objectives in place) and retinal imaging top view (with sample objective removed, at the location indicated by the dashed line box), which is capable of imaging both anterior and posterior eye, in both static mode to image morphology or time-lapse mode to image blood flow. (d) Locking plane procedure. FFOCT images are acquired over an axial extension of 10 μm with 0.5 μm steps and are then cross-correlated with the target image. The sample is then axially translated to the position corresponding to the maximum of the cross-correlation. This example is illustrated with retinal cells.
Table 1.
Setup characteristics.
2.4. Image computation
FFOCT images presented here are constructed using the 2-phase stepping algorithm. FFOCT images, as well as OCT images, exhibit speckle that is due to the random positions of the back scatterers. In this situation a 2-phase stepping algorithm is enough to recover the FFOCT signal, and moreover 2-phase acquisitions are faster. The method to compute the D-FFOCT images (Fig. 2) is explained in [10] for both grayscale and colored dynamic images. Briefly, grayscale images are constructed from a (Nx, Ny, Nt) tensor, where (Nx, Ny) is the camera sensor dimension and Nt is the number of frames recorded, by using a standard deviation sliding window on the time dimension and then averaged to obtain an image. Colored images are computed in the Fourier domain. The temporal variation of each pixel is Fourier transformed and then integrated between [0, 0.5] Hz to form the blue channel, between [0.5, 5] Hz to for the green channel and integrated over 5Hz for the red channel. The arbitrary selection of which frequencies to assign to which color bands aims to subjectively optimize the visualization in RGB, meaning that color scales are non quantitative. Note that the maximal detectable frequency of the phase fluctuations depends on the acquisition speed and is typically 50 Hz for biological samples (corresponding to the Shannon sampling theorem for an acquisition framerate of 100 frames.s−1).
Fig. 2.
(a) 3D reconstruction of a D-FFOCT image stack in explanted macaque retina over a 120 by 120 μm field of view. Note that FFOCT signal is damped with increasing penetration depth, so that upper retinal layers are more clearly visible than lower ones. (b, c, e) En-face images of the (b) inner nuclear layer, (c) outer nuclear layer and (e) photoreceptor layer presenting a similar appearance to two-photon fluorescence imaging [32] and (d) reconstructed cross-section at the location represented by the red dotted line in (a). The cross-section in (d) was linearly interpolated to obtain a unitary pixel size ratio. (f) D-FFOCT image of a porcine retinal pigment epithelium cell culture [31]. (g) Overlay of colored D-FFOCT and FFOCT at the interface between the layers of the nerve fibers (white arrows point to nerve bundles that are very bright in static and invisible in dynamic mode), ganglion cells (blue and green cells, visible in dynamic mode) and inner plexiform (fibrous network, bottom left, visible in static mode). Samples were maintained in vitro in culture medium at room temperature during imaging.
2.5. Computing and displaying temporal variations in time-lapse sequences
Due to its non-invasive nature, FFOCT can be used to acquire time-lapse sequences at a fixed plane and position over long periods to assess slow dynamics on in-vitro samples, or over short periods in-vivo to assess fast dynamics such as blood flow. This data can be displayed in movie format to visualize movement ( Visualization 1 (4.4MB, mp4) and Visualization 2 (2.8MB, mp4) ), or can be processed to quantify the movement speed and directionality of target features (Figs 3, 4). There are two main methods to extract quantitative information on motion in image sequences. The first method is solving the optical flow equations. Optical flow is the pattern of apparent motion of objects, surfaces, and edges in a visual scene. The second type of method is to use block-matching algorithms where the underlying supposition behind motion estimation is that the patterns corresponding to objects and background in a frame of video sequence move within the frame to form corresponding objects on the subsequent frame. The former technique is a differential method where a partial differential equation is solved with typical constraints whereas the latter looks to maximize the correlation between blocks of given size between each frame. We tested block-matching methods with phase correlation and normal correlation, as well as differential methods with different regularizers. The one that gave the best result for our corneal wound healing data-set was the Horn–Schunck method [29] which solves the optical flow equations by optimizing a functional with a regularization term expressing the expected smoothness of the flow field. This algorithm is particularly suitable to extract motion on diffeomorphisms which are differentiable maps (i.e. smooth, without crossing displacement fields). Block-matching methods, in addition to being slow for high-resolution images, were failing due to the apparent homogeneity of the intracellular signals requiring blocks of great size, decreasing the accuracy and leading to very long computations. On the contrary, Horn-Shunck regularization considers the image as a whole and provides a regularizing term that controls the expected velocity map smoothness. The optical flow problem consists of solving the following equation:
| (11) |
where Ix, Iy and It are the spatiotemporal image brightness derivatives, and u and v are the horizontal and vertical optical flow, respectively. This is an equation in two unknowns that cannot be solved as such. This is known as the aperture problem. To find the optical flow another set of equations is needed and Horn-Shunck regularization introduces the following functional:
| (12) |
where and are the spatial derivatives of the optical velocity v, and the regularizer α scales the global smoothness term. The idea is to minimize the optical flow problem by penalizing flow distortions, where the amount of penalization is controlled by the constant α. This constant gives weight to the right integral term which corresponds to the optical flow Laplacian summed over the whole image, thus containing information on the total flow unsmoothness. The functional is then easily optimized because of its convex nature:
| (13) |
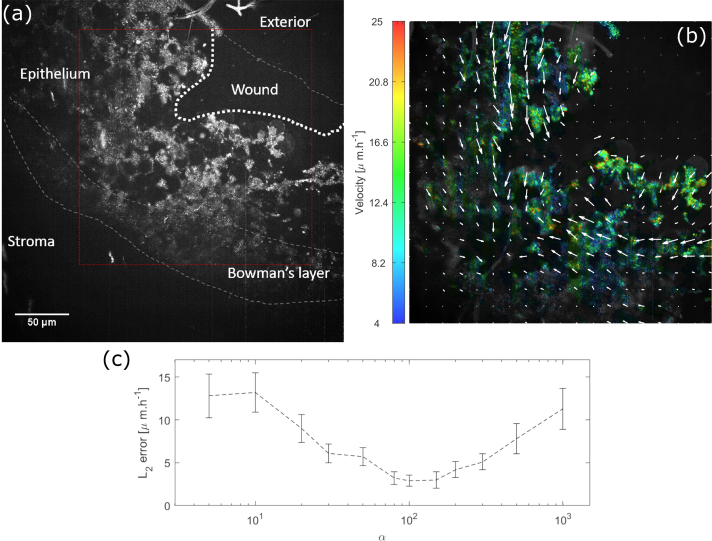
For the wound healing migration problem we optimized α by looking at the L2 error between the velocities computed by the algorithm and 200 manually tracked voxels, see Fig. 3(c). The optimal α was found to be 100.
Fig. 3.
(a) Dynamic grayscale image of a wounded macaque cornea - the red box shows where the computation is done, see Visualization 1 (4.4MB, mp4) (b) Same dynamic image superimposed with colors coding for the cell migration velocity averaged over the 112 minute acquisition. Each arrow represents the mean motion in a pixel - (c) Velocity errors for different Horn-Shunk smoothness terms α. The curve represents the mean error we found by comparing the optical flow computation with 200 manually tracked voxels. Error-bars represent the error standard deviation. The optimal α was found to be 100.
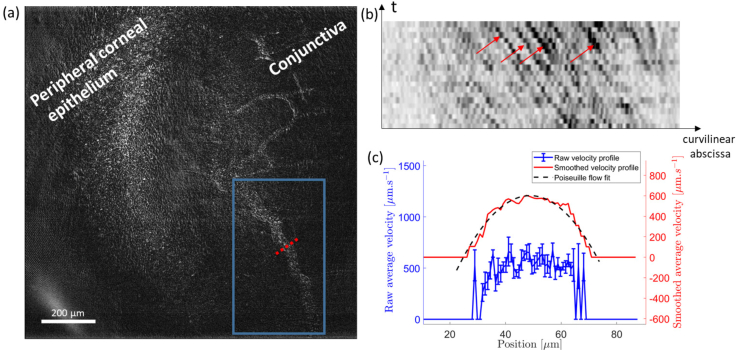
Fig. 4.
(a) Single FFOCT-frame of conjunctival blood flow near the limbal region of the in vivo anterior human eye. See Visualization 2 (2.8MB, mp4) for a movie of blood flow in the drawn box. (b) Kymograph plot (space-time domain) inside the blood vessel at x = 10 μm. Grayscale is inverted so that the black particles indicated by the red arrows are red blood cells flowing into the vessel. The slope corresponds to the particle speed. (c) Raw velocity profile inside the blood vessel (blue) computed along the dotted line in (a) with the method explained in Section 2.6. The standard error is calculated at each position and ranges around 50 μm.s−1 at the center of the profile and 200 μm.s−1 on the sides. The smoothed profile (red) with the fit to a Poiseuille flow profile (black dashed line) are superimposed and voluntarily shifted up for increased visibility.
2.6. Blood flow measurement with FFOCT
For our in vivo blood flow dataset, automated methods based on optical flow failed to extract a velocity map due to the speckle pattern of the images inside vessels. Motion no longer corresponded to a diffeomorphism field, especially locally, leading to a complete divergence of the previous algorithm even with smaller α. Nonetheless we succeeded in extracting a velocity profile inside a vessel using a kymograph plot, i.e. plotting the vessel curvilinear abscissa against time. On such a plot, each event (i.e. a passing particle, such as a blood cell) produces a line, and the slope of this line corresponds to the speed. Using a custom segmentation algorithm, we automatically fit these lines and extracted the speed for each event at a given vessel cross-position. We averaged the speed over the 4 to 18 detected events at each position, and calculated the standard error at each position to evaluate the error in the average speed calculation. Ultimately, the profile can be smoothed and fit to a Poiseuille flow, typically observed in capillaries [30] to extract the maximal velocity vmax defined by:
| (14) |
where r is the axial distance to the center of the capillary and Rcap is the capillary radius. This fit allows averaging over more than 400 tracked events and reduces the error on the maximal blood flow velocity from ±50 μm.s−1 in a single position down to ±15 μm.s−1.
2.7. Samples and subjects
All animal manipulation was approved by the Quinze Vingts National Ophthalmology Hospital and regional review board (CPP Ile-de-France V), and was performed in accordance with the ARVO Statement for the Use of Animals in Ophthalmic and Vision Research. Macaque and porcine ocular globes were obtained from a partner research facility and transported to the Vision Institute in CO2-free neurobasal medium (Thermo Fisher Scientific, Waltham, MA, USA) inside a device that maintained oxygenation, for transport to the laboratory for dissection. We imaged a 2 mm2 piece of peripheral macaque retina, prepared as described in [10]. Briefly, an incision was made in the sclera to remove the anterior segment. The retina was gently removed from the choroid, with separation occurring at the RPE, and flattened into petals by making four incisions (nasal, temporal, superior, inferior). Pieces approximately 3 mm from the fovea toward the median raphe were selected for imaging. We also imaged a porcine retinal pigment epithelium cell culture, prepared as described in [31]. Briefly, porcine eyes were cleaned from muscle, and incubated during 4 minutes in Pursept-AXpress (Merz Hygiene GmbH, Frankfurt, Germany) for disinfection. The anterior portion was cut along the limbus to remove the cornea, lens and retina. A solution containing 0.25% trypsin-EDTA (Life Technologies, Carlsbad, CA, USA) was introduced for 1 hour at 37°C in the eyecup. RPE cells were then gently detached from the Bruch’s membrane and resuspended in Dulbecco’s Modified Eagle medium (DMEM, Life Technologies) supplemented with 20% Fetal Bovine Serum (FBS, Life Technologies) and 10 mg.ml−1 gentamycin (Life Technologies). Cells were allowed to grow in an incubator with a controlled atmosphere at 5% CO2 and 37°C. Samples were placed in transwells, and immersed in CO2-free neurobasal and HEPES (Thermo Fisher Scientific, Waltham, MA, USA) medium for imaging. Fluorescent labeling in RPE cultures used a polyanionic green fluorescent (excitation/emission 495 nm/ 515 nm) calcein dye (LIVE/DEAD Viability/Cytotoxicity Kit, Thermo Fischer Scientific, France) which is well retained within live cells. For in vitro setups, typical power incident on the sample surface is approximately 0.1mW, though this varies from sample to sample as the power level is adapted to work close to saturation of the camera for each experiment.
Using the new combined anterior/posterior setup (Fig. 1(c)) similar to those described in [19,23], in vivo imaging was performed on a healthy volunteer who expressed his informed consent, and the experimental procedures adhered to the tenets of the Declaration of Helsinki. For in vivo imaging, thorough calculations of light safety according to the appropriate standards are available in [23]. Weighted retinal irradiance of our setup is 49 mW.cm−2, corresponding to 7% of the maximum permissible exposure (MPE), and corneal irradiance is 2.6 W.cm−2, corresponding to 65% of the MPE, which is further reduced by operating the light source in pulsed mode.
3. Results
3.1. Subcellular contrast enhancement and dynamics detection in retinal explants and cell cultures
FFOCT and D-FFOCT are useful to reveal contrast inside transparent tissue such as retina. We imaged a fresh retinal explant from macaque with the inverted setup shown Fig. 1(b). We acquired 100 μm deep FFOCT and D-FFOCT stacks with 1 μm step leading to stacks of 101 en-face images. Fig. 2 shows a 3D volume, en face slices and a reconstructed cross sectional view from this acquisition. Fig. 2(a–e) show the contrast enhancement in D-FFOCT on cellular features in layers such as the inner and outer nuclear and photoreceptor layers. Fig. 2(g) demonstrates the complementarity of static and dynamic FFOCT modes, for example to understand the disposition of nerve fibers and inner plexiform structures (visible in static mode) in relation to ganglion cells (visible in dynamic mode). In comparison to the stack acquisition performed in past setups [10], the improved immobilisation of the sample in the new inverted multimodal setup facilitated automated acquisition of 3D stacks with reliable micrometer steps so that volumetric and cross-sectional representations (Fig. 2(a, b)) may be constructed to improve understanding of retinal cellular organization. The automated plane locking procedure to correct for axial drift means that we are able to repeatedly acquire 3D stacks beginning at the exact same plane, making 3D time-lapse imaging possible and ensuring perfect coincidence of multimodal FFOCT/D-FFOCT stacks. In addition to volumetric imaging through bulk tissue, D-FFOCT can also be used to image 2D cell cultures to monitor culture behavior over time. An en face image of a 2D retinal pigment epithelium cell (RPE) culture (Fig. 2(f)) shows high contrast on cell nuclei and cytoplasm and enables identification of multinucleated cells or cytoplasmic variations from cell to cell. As a result of the improvements in sample stability and time-lapse acquisition offered by the inverted setup, time-lapse imaging over periods of hours, in conjunction with the fast dynamic signal which creates the D-FFOCT contrast in a single acquisition, can now be reliably performed. This allows us to identify dynamic behavior at various time scales in these in vitro conditions over time. We can therefore follow in vitro cellular decline in situ in explanted tissues, or in vitro cellular development in a growing culture. These capabilities allow understanding of retinal organization and monitoring of cell viability in disease modeling applications or quality control of cultured tissue for graft.
3.2. Slow dynamics: corneal wound healing imaging
To demonstrate the potential benefits of time-lapse D-FFOCT we imaged a corneal wound. A macaque cornea was maintained in graft storage conditions, i.e. at room temperature in graft transport medium (CorneaJet, Eurobio, France), during imaging. Epithelium was scraped in a small region of the corneal surface using tweezers, creating a wound in the epithelial layer. The acquired time-lapse sequence in the epithelial layer showed that in addition to revealing epithelial cells and their arrangement, we were also able to detect the slow corneal healing with the migration of cells to fill the wound. We acquired 112 dynamic images in a time-lapse fashion on a wounded macaque cornea with the method and setup introduced in [7], but with the inverse configuration, as described in Section 2.3 above. The acquisition duration was 112 minutes, corresponding to 1 minute between each dynamic image (see Visualization 1 (4.4MB, mp4) ). We optimized the grayscale range of the dynamic image by applying a non-local mean filter to remove the noise while preserving the edges and then averaged 8 images leading to a stack composed of 14 grayscale images. We computed 13 optical flow maps (between each of the 14 frames) and summed them to compute the motion map, see Fig. 3(b). The velocities measured range between 10 − 25 μm.h−1 from near the wound center to periphery respectively. In the literature, epithelial cell migration speed in vivo in wound healing is around 50 μm.h−1 and lower when the wound is starting to close [33]. Our figures are therefore of a similar order of magnitude, although lower, possibly as we were imaging ex-vivo samples at 25°C instead of in vivo cornea at 37°C and imaged close to an almost closed wound. Indeed, our measured migration rates are closer to those reported for similar in vitro reepithelialization cell migration studies in rabbit (10 − 16 μm.h−1 [34]). Our algorithm was validated by comparing with manual tracking of 200 voxels in cells on successive images. Using the previous errors computation presented in Section 2.5 with α = 100 we obtained an accuracy of 2.9 ± 0.6 μm.h−1.
3.3. Fast dynamics: blood flow in vivo anterior eye
The fast acquisition speed allows FFOCT to obtain images in vivo and estimate velocities of physiological processes. Fig. 4 and Visualization 2 (2.8MB, mp4) depict FFOCT images of conjunctival blood flow in the in vivo human eye. Images were obtained using a fast acquisition at 275 frames.s−1 [23] followed by template-matching with an ImageJ plugin to remove lateral misalignment [35, 36]. Flow was quantified using the method described in Section 2.6. The measured flow profile was fitted to a Poiseuille flow profile with good accuracy (R2 > 0.95) and showed a maximal velocity of 600 ± 15μm.s−1 (Fig. 4(c)), where both speed and diameter are in agreement with previous experimental findings in the literature, which used slit-lamp microscopy, coupled with a CCD camera [24,37]. The accuracy of our technique seems to outperform the accuracy we can estimate from other existing techniques to measure blood flow in the eye by about one order of magnitude [24–26].
3.4. Towards label free non invasive specific imaging
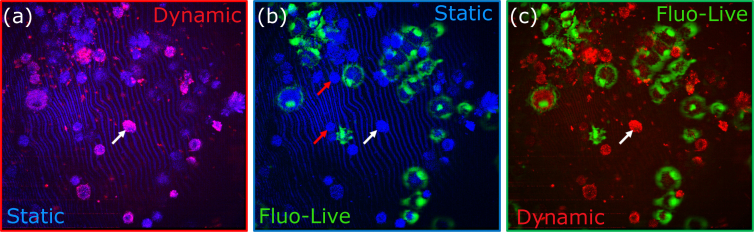
Multimodal setups that combine fluorescence microscopy and OCT have been developed [38,39] in order to combine the targeted contrast of fluorescent dyes and antibodies with the structural contrast of OCT. Recently, a multimodal setup (Fig. 1(a)) was proposed to combine static and dynamic FFOCT with fluorescence microscopy [40]. This setup can be used to confirm the FFOCT identity of specific cell types or behaviours via comparison with the fluorescent signal. Simultaneous coincident imaging on a single multimodal setup is vital in order to correctly identify the cells at the pixel to pixel scale and so remove any uncertainty that can occur when imaging one sample on multiple microscopes. To illustrate this validation approach, we labelled living retinal pigment epithelium (RPE) cells in a sparse culture, using calcein dye. The polyanionic dye calcein is well retained within live cells, producing an intense uniform green fluorescence in live cells. We jointly acquired FFOCT, D-FFOCT and fluorescence images of the labeled cells, in order to compare the different modalities within the same plane at precisely the same time. Static FFOCT provided the baseline information about cell presence. The refractive index mismatch between the culture medium and the cells induces light backscattering from cells measured by FFOCT. Dynamic FFOCT highlights areas where there is motion of back-scatterers (e.g. mitochondria), indicating that the cell metabolism was somewhat active. Fluorescence images showed which cells were alive when we carried out the labelling procedure. The results are shown in Fig. 5 by merging each channel by pairs: (a) merges static FFOCT and dynamic FFOCT, highlighting the active cells over all the cells; (b) merges the static and fluorescently labeled live cells, validating successful labeling as only a subset of cells are fluorescent; (c) merges dynamic FFOCT and fluorescently labeled live cells allowing the comparison between live, dead and dying cell dynamics. As shown in Fig. 5(a–c), we thereby observed 3 different configurations: i) Active cells exhibiting fluorescence indicating that these cells were alive (green in b, c); ii) Inactive cells without fluorescence indicating that these cells were dead (red arrows in Fig. 5(b,c)); iii) Highly active cells without fluorescence suggesting that the cell was dying (white arrows on Fig. 5(a–c)).
Fig. 5.
Multimodal binary merging. Static FFOCT is represented in blue, dynamic FFOCT in red and living labeled cells in green, imaged with the fluorescence setup presented Fig. 1(a). White arrows show active cells without fluorescence suggesting that apoptosis was occuring. Red arrows show inactive cells without fluorescence indicating that these cells were dead.
4. Discussion
Through these examples of multimodal static and dynamic FFOCT images, we have demonstrated the imaging of multiple spatial scales of morphology and temporal scales of dynamic processes in the eye with multimodal FFOCT. However in order for the technique to be adopted by the microscopy and medical communities as true label-free microscopy, validation is required in relation to existing techniques. In addition, further technical improvements could be made with regards to improving efficiency of data management to enable real-time dynamic imaging and improve real-time in vivo image display.
4.1. Towards label free dynamic FFOCT
Using the validation approach of fluorescent labeling in tandem with static and dynamic FFOCT to identify the dynamic signature for specific cell behaviors or types should allow us to achieve reliable true label-free imaging in 3D tissue samples with FFOCT alone. The proof of concept presented in Section 3.4 was a first step toward label free imaging as we only used the dynamic image which is the result of a strong dimension reduction. Indeed, in order to construct an image, we map the dynamic signal over one or three dimensions depending on the desired output (i.e. grayscale or color image). The next step is to consider the full signal in order to train machine learning algorithms to find the optimal signal representation that could distinguish cells based on different criteria, e.g. live, dead and undergoing apoptosis. We hope that by studying the dynamic distribution inside cells it will be possible to extract more information such as cell cycle, cell type, etc. making D-FFOCT a powerful tool for cell biology.
4.2. Towards real time dynamic FFOCT
Currently each dynamic image is computed in approximately 10 seconds on a GPU (NVidia Titan Xp). Most of this time is dedicated to memory management. In the original D-FFOCT configuration [7], images were computed using the CPU so the frame grabber was configured to save data directly on the computer Random Access Memory (RAM). The difficulty for real-time applications is the data transfer bottleneck. Indeed, a GPU can process data only as fast as the data can be transferred to it. In traditional system memory models, each device has access only to its own memory so that a frame grabber acquires to its own set of system buffers. Meanwhile, the GPU has a completely separate set of system buffers, so any transfer between the two must be performed by the CPU, which take times if the amount of data is important. Our current framework waits for the image to be completely copied to the RAM and then transfers it to the GPU which limits the maximal system speed. The average load of the GPU during the overall procedure is less than 5%. In the near future we plan to take advantage of the latest advance in GPU computing and establish a direct link between the frame grabber and the GPU memory. Taking the Titan Xp as reference and being limited only by the computation, we expect to be able to achieve real-time dynamic images. We hope that real-time dynamic movies could highlight new biological behavior at the cellular and subcellular level. In addition, the faster processing will improve our real-time in vivo image display.
5. Conclusion
We have demonstrated detection of slow and fast dynamic processes in the eye thanks to recent technological progress in multimodal full-field optical coherence tomography. Combined static, dynamic and fluorescence contrasts are moving towards the goal of achieving label-free high-resolution imaging of anterior eye and retina with temporal resolution from milliseconds to several hours. Its contactless and non-destructive nature makes FFOCT a useful technique both for following in vitro sample evolution over long periods of time and for imaging of the human eye in vivo.
Acknowledgments
The authors would like to thank Valérie Fradot and Djida Ghoubay at the Vision Institute for sample preparation, and helpful advice and discussion on biology aspects, and Michel Paques and Vincent Borderie at the Quinze Vingts Hospital for helpful discussions.
Funding
HELMHOLTZ grant, European Research Council (ERC) (610110).
Disclosures
CB: LLTech SAS (I), K. Groux: LLTech SAS (E), others: none.
References
- 1.Huang D., Swanson E., Lin C., Schuman J., Stinson W., Chang W., Hee M., Flotte T., Gregory K., Puliafito C., et al. , “Optical coherence tomography,” Science 254, 1178–1181 (1991). 10.1126/science.1957169 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Drexler W., Fujimoto J. G., eds., Optical Coherence Tomography: Technology and Applications (Springer, 2015), 2nd ed. 10.1007/978-3-319-06419-2 [DOI] [Google Scholar]
- 3.Beaurepaire E., Boccara A. C., Lebec M., Blanchot L., Saint-Jalmes H., “Full-field optical coherence microscopy,” Opt. Lett. 23, 244–246 (1998). 10.1364/OL.23.000244 [DOI] [PubMed] [Google Scholar]
- 4.Dubois A., Grieve K., Moneron G., Lecaque R., Vabre L., Boccara C., “Ultrahigh-resolution full-field optical coherence tomography,” Appl. Opt. 43, 2874–2883 (2004). 10.1364/AO.43.002874 [DOI] [PubMed] [Google Scholar]
- 5.Ben Arous J., Binding J., Léger J.-F., Casado M., Topilko P., Gigan S., Boccara A. C., Bourdieu L., “Single myelin fiber imaging in living rodents without labeling by deep optical coherence microscopy,” Journal of Biomedical Optics 16, 116012 (2011). 10.1117/1.3650770 [DOI] [PubMed] [Google Scholar]
- 6.Jain M., Shukla N., Manzoor M., Nadolny S., Mukherjee S., “Modified full-field optical coherence tomography: A novel tool for rapid histology of tissues,” J. Pathol. Informatics 2, 28 (2011). 10.4103/2153-3539.82053 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Apelian C., Harms F., Thouvenin O., Boccara A. C., “Dynamic full field optical coherence tomography: subcellular metabolic contrast revealed in tissues by interferometric signals temporal analysis,” Biomed. Opt. Express 7, 1511–1524 (2016). 10.1364/BOE.7.001511 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Lee J., Wu W., Jiang J. Y., Zhu B., Boas D. A., “Dynamic light scattering optical coherence tomography,” Opt. Express 20, 22262–22277 (2012). 10.1364/OE.20.022262 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Leroux C.-E., Bertillot F., Thouvenin O., Boccara A.-C., “Intracellular dynamics measurements with full field optical coherence tomography suggest hindering effect of actomyosin contractility on organelle transport,” Biomed. Opt. Express 7, 4501–4513 (2016). 10.1364/BOE.7.004501 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Thouvenin O., Boccara C., Fink M., Sahel J., Pâques M., Grieve K., “Cell motility as contrast agent in retinal explant imaging with full-field optical coherence tomography,” Investig. Opthalmology & Vis. Sci. 58, 4605 (2017). 10.1167/iovs.17-22375 [DOI] [PubMed] [Google Scholar]
- 11.Nahas A., Tanter M., Nguyen T.-M., Chassot J.-M., Fink M., Boccara A. C., “From supersonic shear wave imaging to full-field optical coherence shear wave elastography,” J. Biomed. Opt. 18, 18(2013). 10.1117/1.JBO.18.12.121514 [DOI] [PubMed] [Google Scholar]
- 12.Binding J., Arous J. B., Léger J.-F., Gigan S., Boccara C., Bourdieu L., “Brain refractive index measured in vivo with high-na defocus-corrected full-field oct and consequences for two-photon microscopy,” Opt. Express 19, 4833–4847 (2011). 10.1364/OE.19.004833 [DOI] [PubMed] [Google Scholar]
- 13.Neil M. A. A., Juškaitis R., Wilson T., “Method of obtaining optical sectioning by using structured light in a conventional microscope,” Opt. Lett. 22, 1905–1907 (1997). 10.1364/OL.22.001905 [DOI] [PubMed] [Google Scholar]
- 14.Mertz J., Introduction to Optical Microscopy, vol. 138 (W. H. Freeman, 2009). [Google Scholar]
- 15.Gustafsson M. G. L., “Nonlinear structured-illumination microscopy: Wide-field fluorescence imaging with theoretically unlimited resolution,” Proc. Natl. Acad. Sci. 102, 13081–13086 (2005). 10.1073/pnas.0406877102 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Auksorius E., Bromberg Y., Motiejūnaitė R., Pieretti A., Liu L., Coron E., Aranda J., Goldstein A. M., Bouma B. E., Kazlauskas A., Tearney G. J., “Dual-modality fluorescence and full-field optical coherence microscopy for biomedical imaging applications,” Biomed. Opt. Express 3, 661–666 (2012). 10.1364/BOE.3.000661 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Thouvenin O., Fink M., Boccara A. C., “Dynamic multimodal full-field optical coherence tomography and fluorescence structured illumination microscopy,” J. Biomed. Opt. 22, 22 (2017). 10.1117/1.JBO.22.2.026004 [DOI] [PubMed] [Google Scholar]
- 18.Xiao P., Fink M., Boccara A. C., “Full-field spatially incoherent illumination interferometry: a spatial resolution almost insensitive to aberrations,” Opt. Lett. 41, 3920–3923 (2016). 10.1364/OL.41.003920 [DOI] [PubMed] [Google Scholar]
- 19.Xiao P., Mazlin V., Grieve K., Sahel J.-A., Fink M., Boccara A. C., “In vivo high-resolution human retinal imaging with wavefront-correctionless full-field oct,” Optica 5, 409–412 (2018). 10.1364/OPTICA.5.000409 [DOI] [Google Scholar]
- 20.Grieve K., Palazzo L., Dalimier E., Vielh P., Fabre M., “A feasibility study of full-field optical coherence tomography for rapid evaluation of EUS-guided microbiopsy specimens,” Gastrointest. Endosc. 81, 342–350 (2015). 10.1016/j.gie.2014.06.037 [DOI] [PubMed] [Google Scholar]
- 21.Grieve K., Paques M., Dubois A., Sahel J., Boccara C., Le Gargasson J.-F., “Ocular tissue imaging using ultrahigh-resolution, full-field optical coherence tomography,” Investig. Ophthalmol. & Vis. Sci. 45, 4126 (2004). 10.1167/iovs.04-0584 [DOI] [PubMed] [Google Scholar]
- 22.Grieve K., Thouvenin O., Sengupta A., Borderie V. M., Paques M., “Appearance of the retina with full-field optical coherence tomography,” Investig. Ophthalmol. & Vis. Sci. 57, OCT96 (2016). 10.1167/iovs.15-18856 [DOI] [PubMed] [Google Scholar]
- 23.Mazlin V., Xiao P., Dalimier E., Grieve K., Irsch K., Sahel J.-A., Fink M., Boccara A. C., “In vivo high resolution human corneal imaging using full-field optical coherence tomography,” Biomed. Opt. Express 9, 557–568 (2018). 10.1364/BOE.9.000557 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Shahidi M., Wanek J., Gaynes B., Wu T., “Quantitative assessment of conjunctival microvascular circulation of the human eye,” Microvasc. research 79, 109–113 (2010). 10.1016/j.mvr.2009.12.003 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Wartak A., Haindl R., Trasischker W., Baumann B., Pircher M., Hitzenberger C. K., “Active-passive path-length encoded (apple) doppler oct,” Biomed. optics express 7, 5233–5251 (2016). 10.1364/BOE.7.005233 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Pedersen C. J., Huang D., Shure M. A., Rollins A. M., “Measurement of absolute flow velocity vector using dual-angle, delay-encoded doppler optical coherence tomography,” Opt. letters 32, 506–508 (2007). 10.1364/OL.32.000506 [DOI] [PubMed] [Google Scholar]
- 27.Sheehy C. K., Yang Q., Arathorn D. W., Tiruveedhula P., de Boer J. F., Roorda A., “High-speed, image-based eye tracking with a scanning laser ophthalmoscope,” Biomed. Opt. Express 3, 2611–2622 (2012). 10.1364/BOE.3.002611 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Vienola K. V., Braaf B., Sheehy C. K., Yang Q., Tiruveedhula P., Arathorn D. W., de Boer J. F., Roorda A., “Real-time eye motion compensation for oct imaging with tracking slo,” Biomed. Opt. Express 3, 2950–2963 (2012). 10.1364/BOE.3.002950 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Horn B. K., Schunck B. G., “Determining optical flow,” Artif. Intell. 17, 185–203 (1981). 10.1016/0004-3702(81)90024-2 [DOI] [Google Scholar]
- 30.Munson B. R., Young D. F., Okiishi T. H., Huebsch W. W., Fundamentals of Fluid Mechanics, vol. 69 John Wiley & Sons, Inc, 520 (2006). [Google Scholar]
- 31.Arnault E., Barrau C., Nanteau C., Gondouin P., Bigot K., Viénot F., Gutman E., Fontaine V., Villette T., Cohen-Tannoudji D., Sahel J.-A., Picaud S., “Phototoxic action spectrum on a retinal pigment epithelium model of age-related macular degeneration exposed to sunlight normalized conditions,” PLOS ONE 8, 1–12 (2013). 10.1371/journal.pone.0071398 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Sharma R., Williams D. R., Palczewska G., Palczewski K., Hunter J. J., “Two-photon autofluorescence imaging reveals cellular structures throughout the retina of the living primate eye,” Investig. Ophthalmol. & Vis. Sci. 57, 632 (2016). 10.1167/iovs.15-17961 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Ashby B. D., Garrett Q., Dp M., “Corneal Injuries and Wound Healing – Review of Processes and Therapies,” Austin J. Clin. Ophthalmol. p. 25 (2014). [Google Scholar]
- 34.Gonzalez-Andrades M., Alonso-Pastor L., Mauris J., Cruzat A., Dohlman C. H., Argüeso P., “Establishment of a novel in vitro model of stratified epithelial wound healing with barrier function,” Sci. Reports 6, 19395 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Schindelin J., Rueden C. T., Hiner M. C., Eliceiri K. W., “The imagej ecosystem: An open platform for biomedical image analysis,” Mol. Reproduction Dev. 82, 518–529 (2015). 10.1002/mrd.22489 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Tseng Q., Duchemin-Pelletier E., Deshiere A., Balland M., Guillou H., Filhol O., Théry M., “Spatial organization of the extracellular matrix regulates cell–cell junction positioning,” Proc. Natl. Acad. Sci. 109, 1506–1511 (2012). 10.1073/pnas.1106377109 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Wang L., Yuan J., Jiang H., Yan W., Cintrón-Colón H. R., Perez V. L., DeBuc D. C., Feuer W. J., Wang J., “Vessel sampling and blood flow velocity distribution with vessel diameter for characterizing the human bulbar conjunctival microvasculature,” Eye & contact lens 42, 135 (2016). 10.1097/ICL.0000000000000146 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Harms F., Dalimier E., Vermeulen P., Fragola A., Boccara A. C., “Multimodal full-field optical coherence tomography on biological tissue: toward all optical digital pathology,” Proc.SPIE 8216, 8216 (2012). [Google Scholar]
- 39.Makhlouf H., Perronet K., Dupuis G., Lévêque-Fort S., Dubois A., “Simultaneous optically sectioned fluorescence and optical coherence microscopy with full-field illumination,” Opt. Lett. 37, 1613–1615 (2012). 10.1364/OL.37.001613 [DOI] [PubMed] [Google Scholar]
- 40.Thouvenin O., Apelian C., Nahas A., Fink M., Boccara C., “Full-field optical coherence tomography as a diagnosis tool: Recent progress with multimodal imaging,” Appl. Sci. 7, 236 (2017). 10.3390/app7030236 [DOI] [Google Scholar]