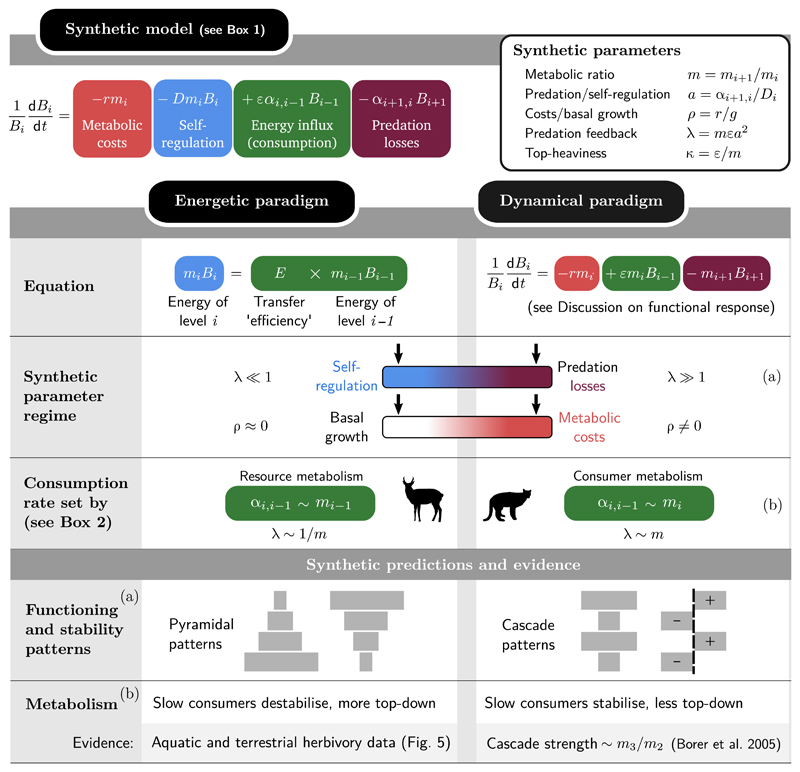
Figure 2.

Synthesising the energetic and dynamical paradigms and deriving systematic predictions. In the energetic paradigm, the biomass B_i of trophic level i is often predicted using the heuristic formula (10) reproduced in the figure. The dynamical paradigm emphasises the role of predators in regulating their prey, and explores the role of different functional responses (Rosenzweig 1971) such as the Lotka–Volterra model (11) shown here. By embedding both paradigms in our synthetic model (defined in Box 1), we can highlight their differences. At equilibrium, dB_i/dt = 0, we can identify the equations term-by-term. Terms are colour-coded by their dependence in B_i, B_i–1 and B_i+1. Each approach emphasises some terms over others, as symbolised by the colour gradients and arrows in ‘Synthetic parameter regime’. We see that the energetic formula (10) neglects predation mortality (λ≪1) and ignores metabolic losses (ρ≈0, equivalent to high basal growth). This leads to pyramidal patterns in various properties, from biomass (Fig. 3) to stability (Fig. 4). On the other hand, the dynamical paradigm emphasises predation loss but ignores consumer self-regulation (right-hand arrows), leading to cascade patterns, that is, alternating patterns of positive and negative, or high and low, values across trophic levels. In addition, the energetic formula assumes that consumption is proportional to resource metabolism, while dynamical models (Brose et al. 2006b) generally assume it is proportional to consumer metabolism (Box 2). This leads to divergent predictions on the role of metabolism in biomass distribution and stability, see main text and Fig. 5. The labels (a) and (b) relate assumptions to predictions.