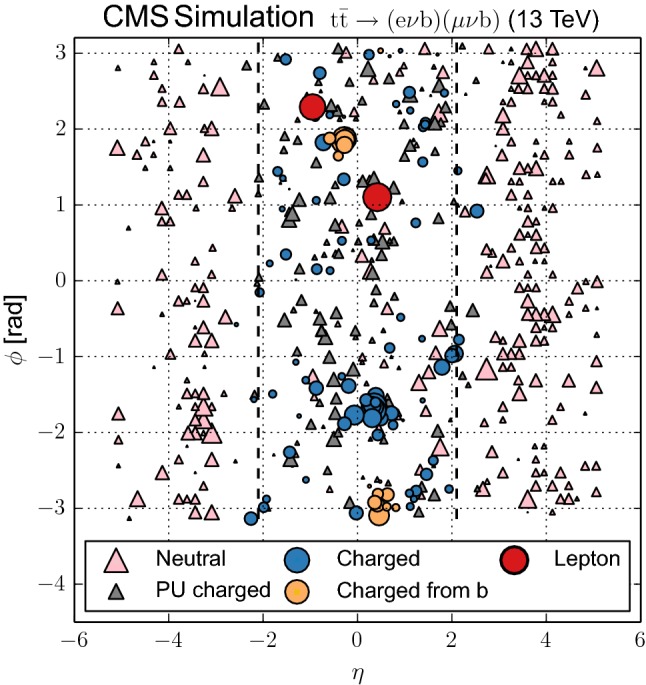
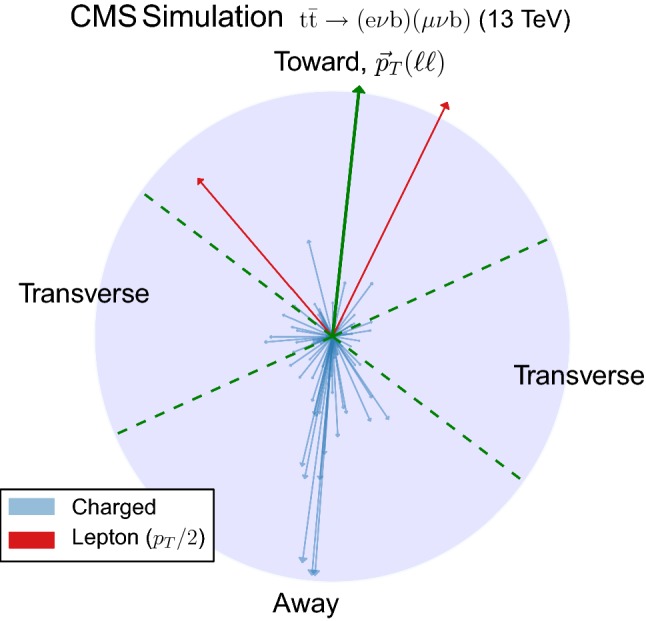
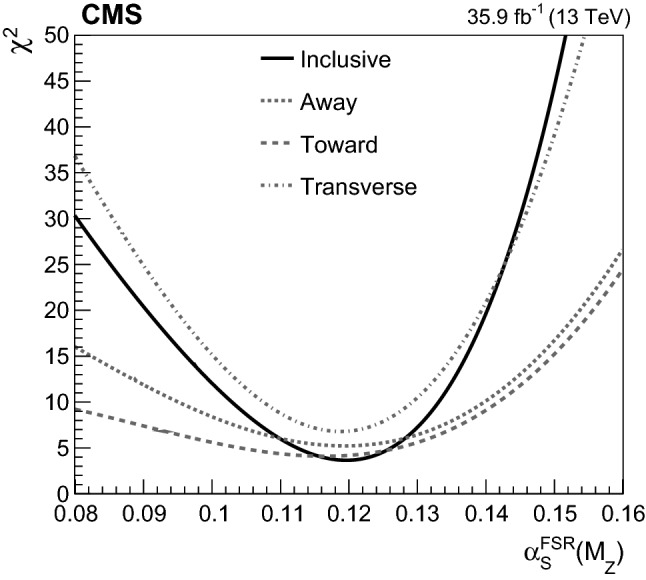
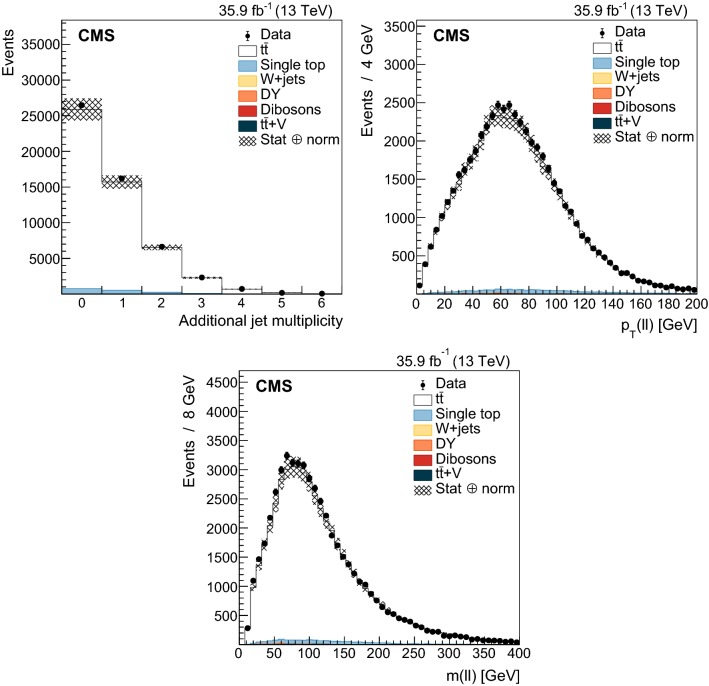
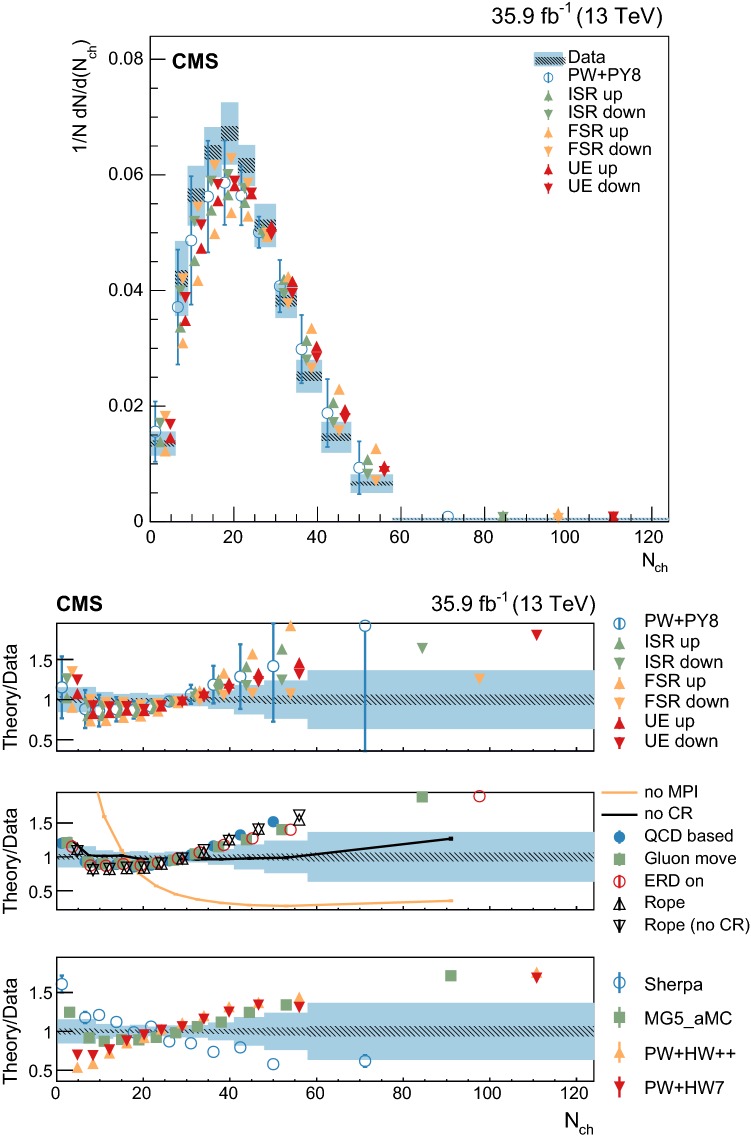
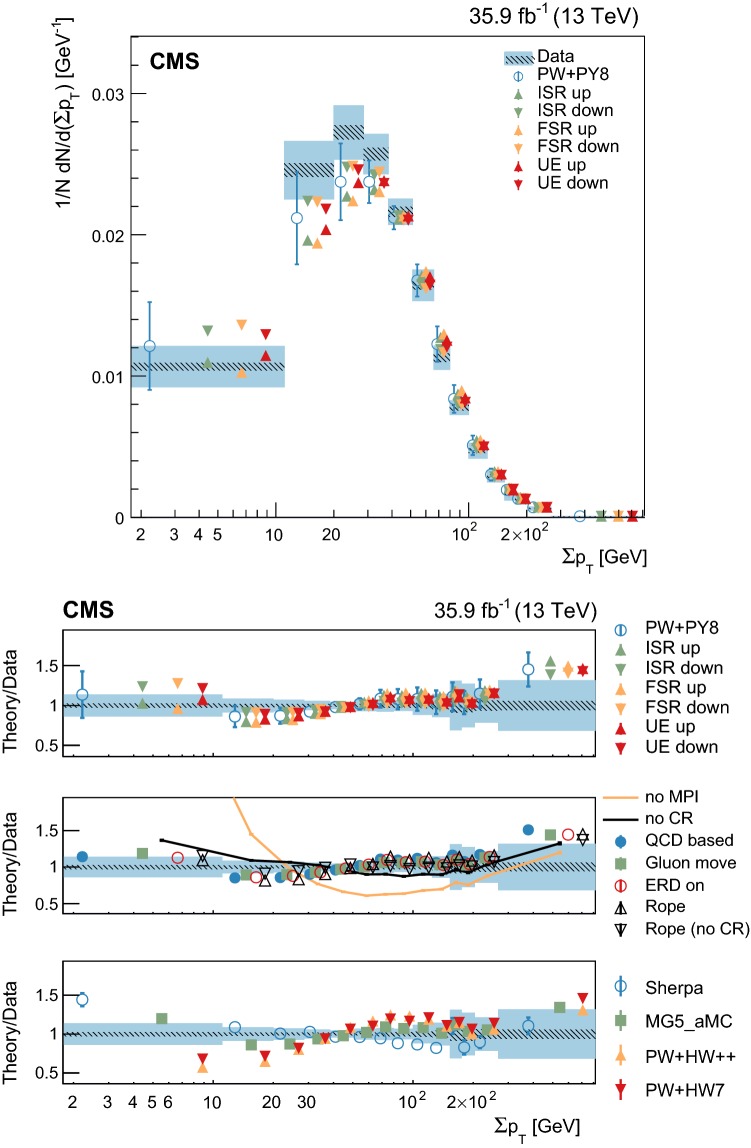
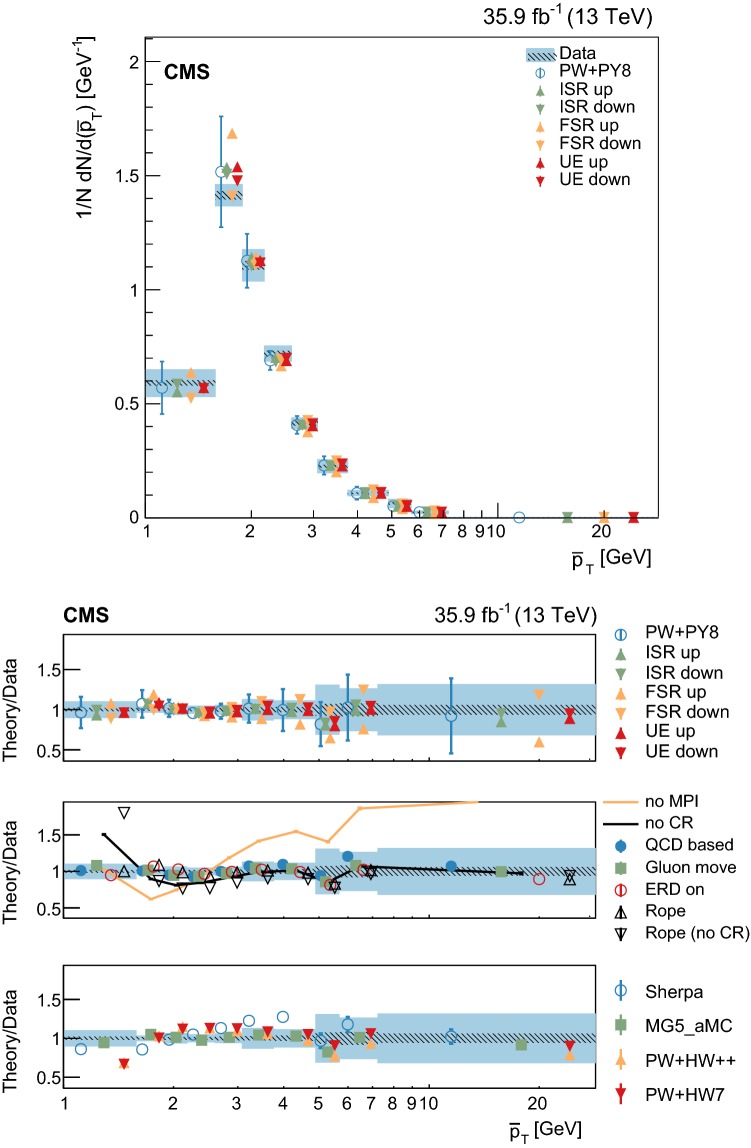
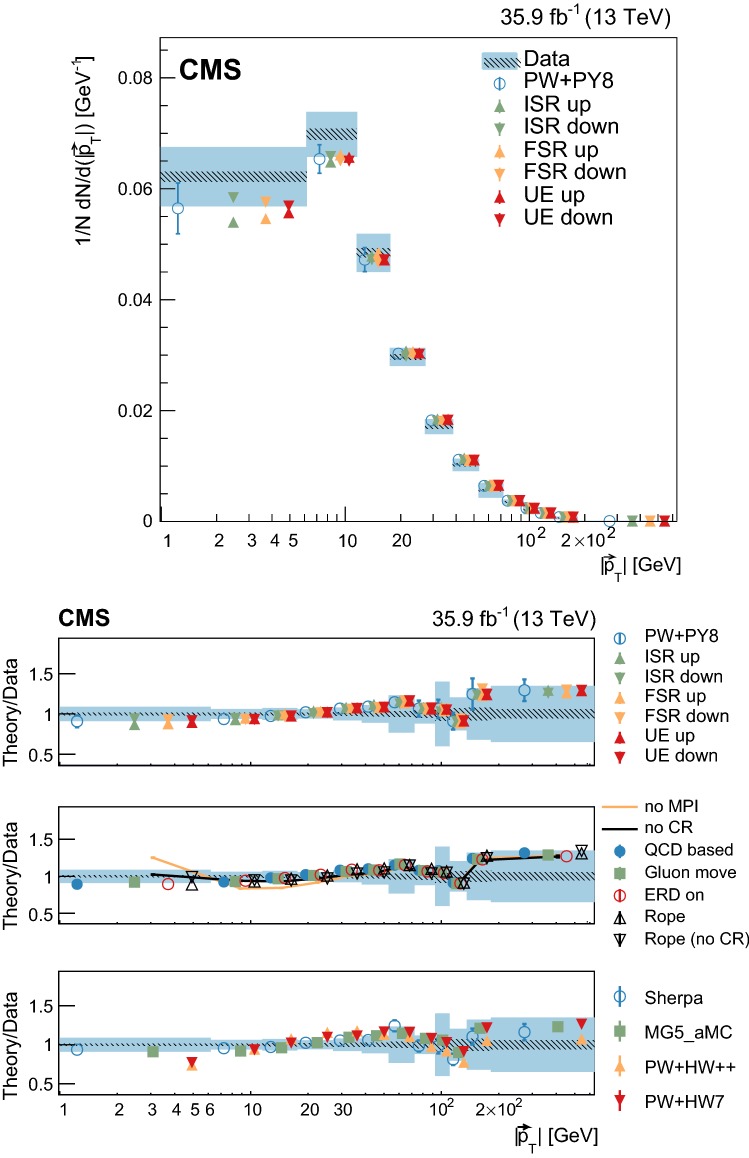
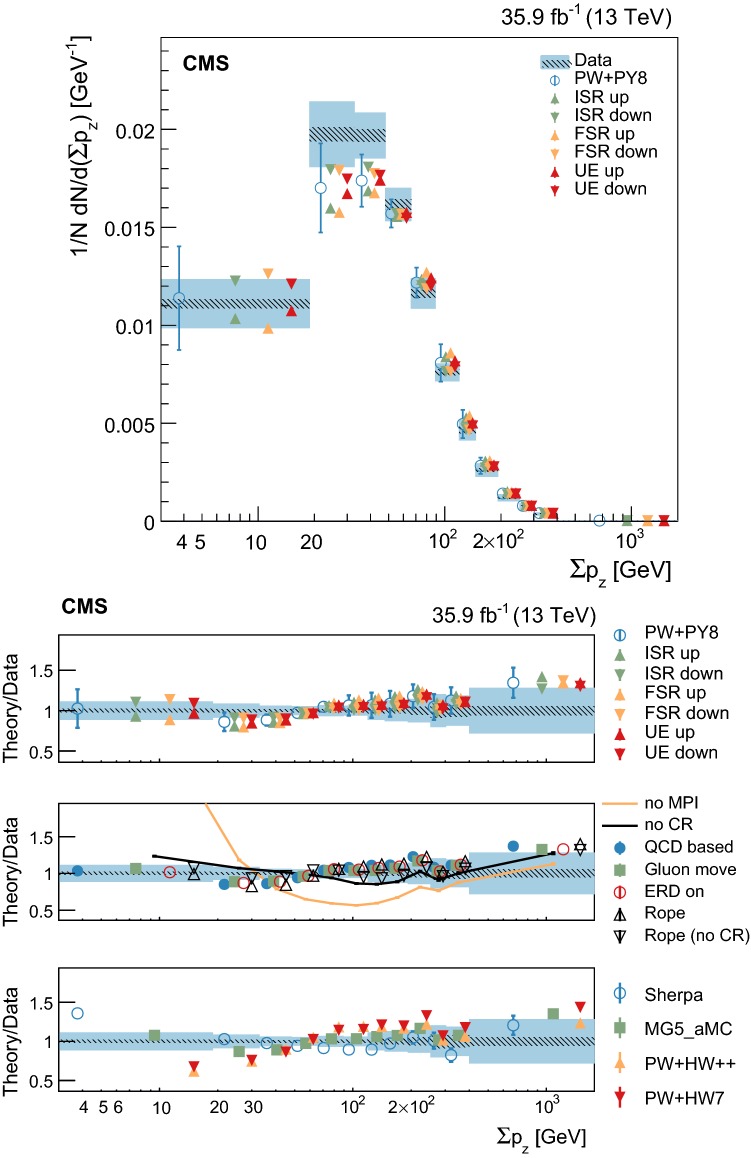
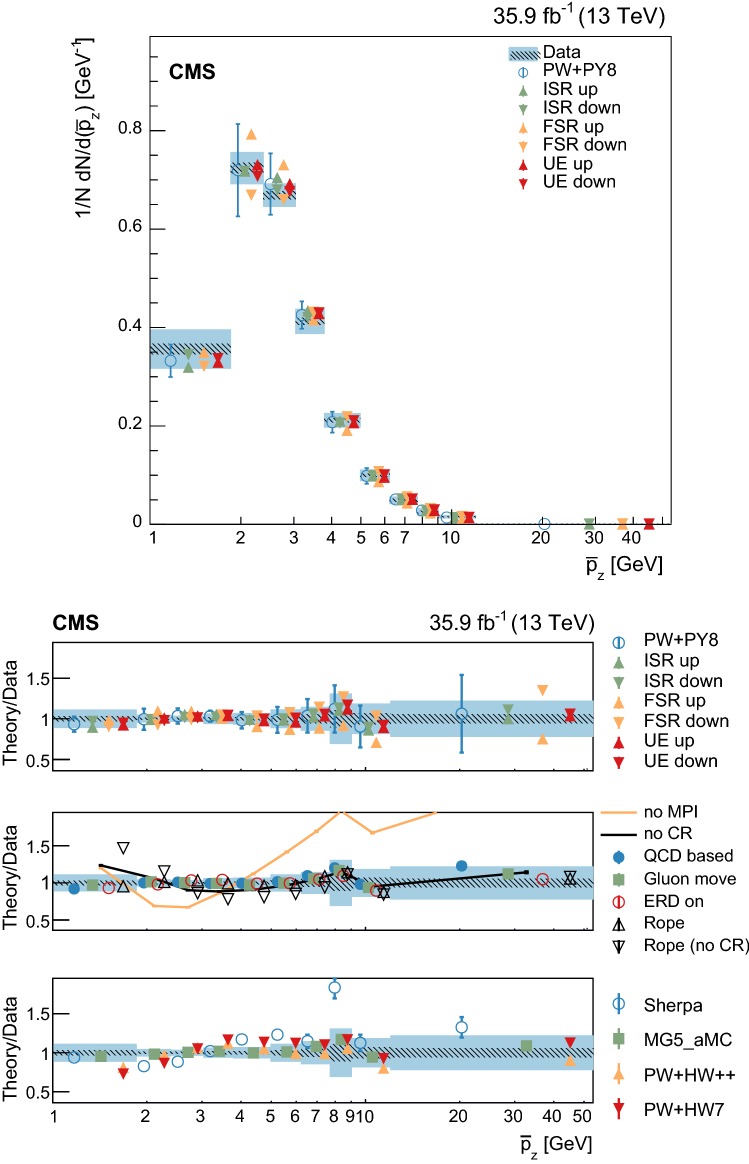
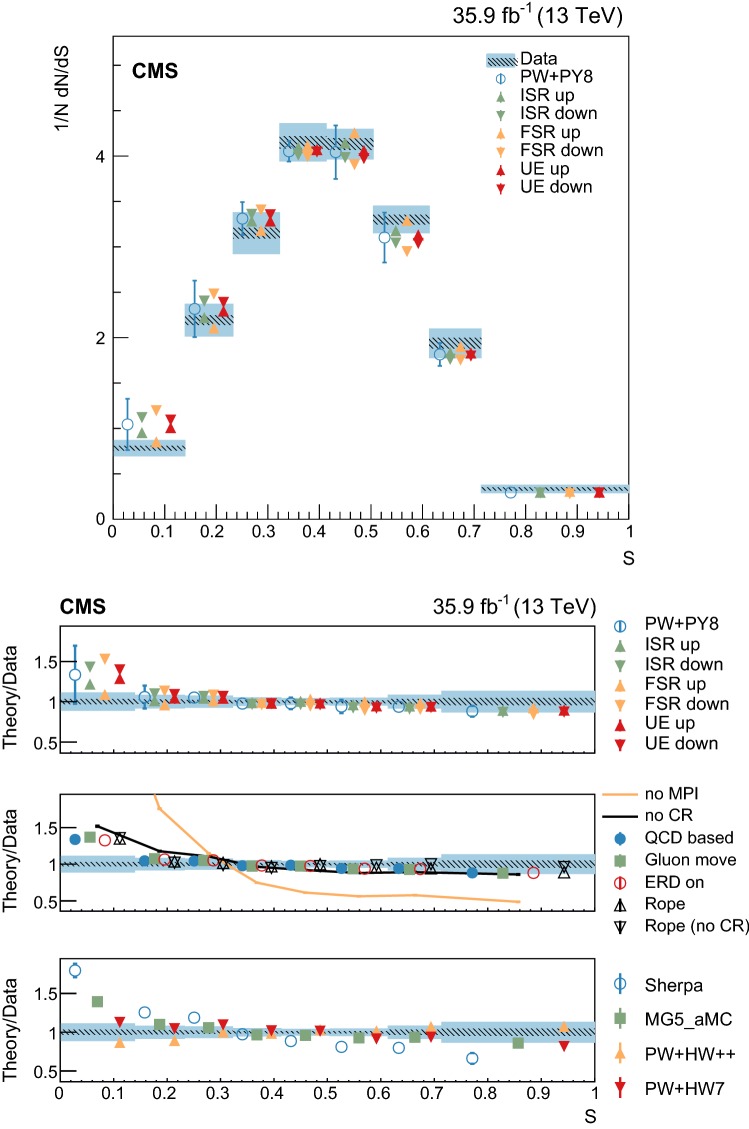
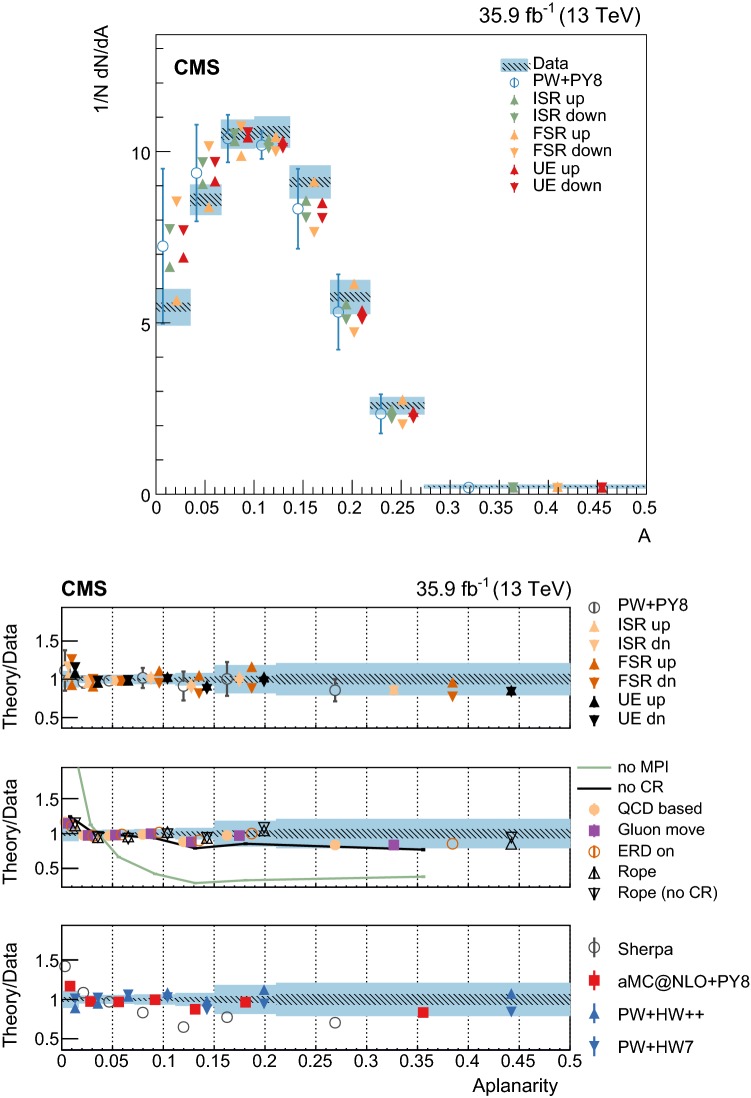
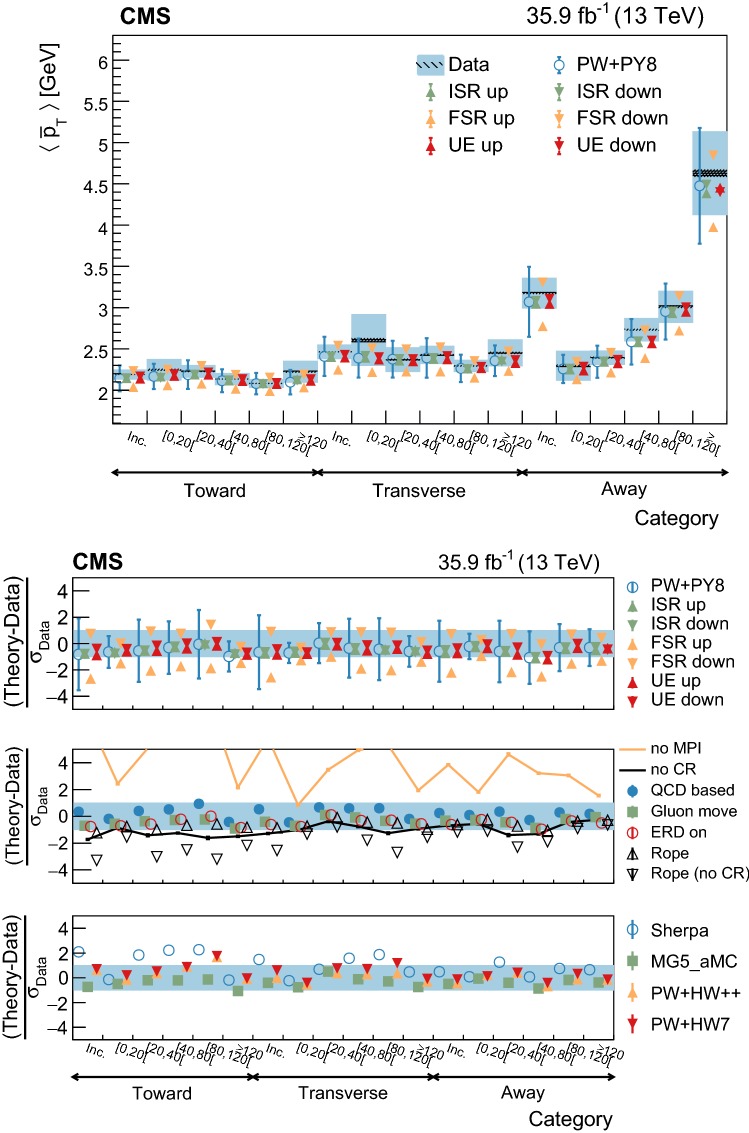
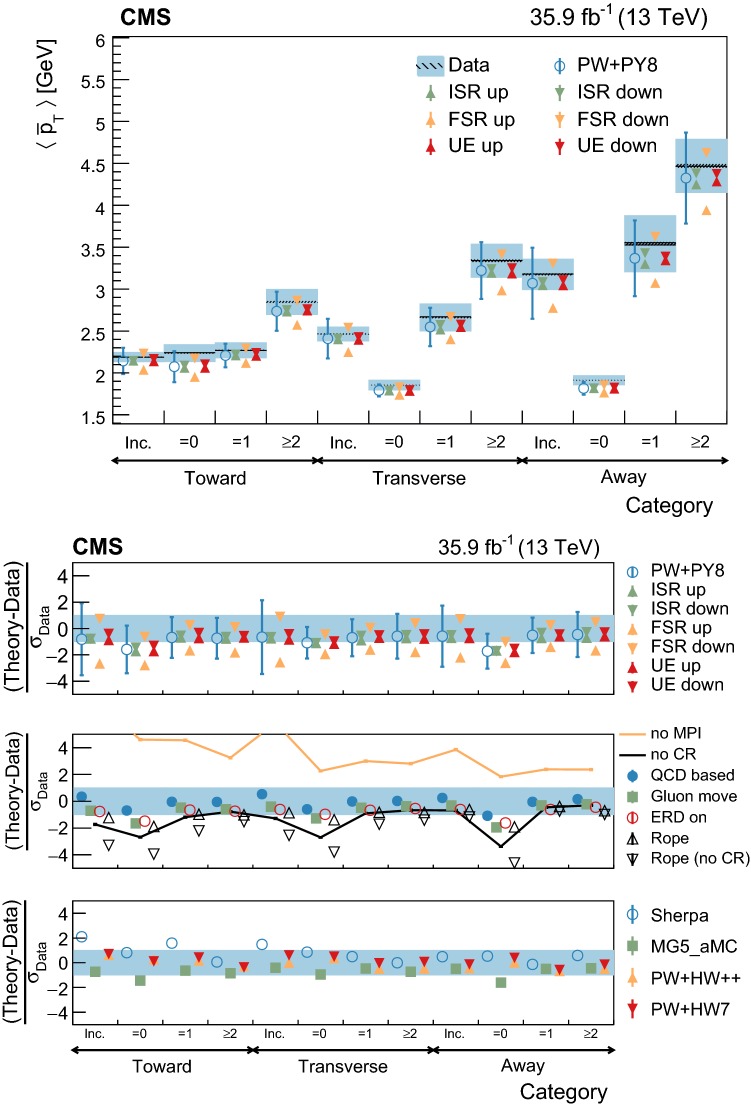
A M Sirunyan
A M Sirunyan
1Yerevan Physics Institute, Yerevan, Armenia
1,
A Tumasyan
A Tumasyan
1Yerevan Physics Institute, Yerevan, Armenia
1,
W Adam
W Adam
2Institut für Hochenergiephysik, Vienna, Austria
2,
F Ambrogi
F Ambrogi
2Institut für Hochenergiephysik, Vienna, Austria
2,
E Asilar
E Asilar
2Institut für Hochenergiephysik, Vienna, Austria
2,
T Bergauer
T Bergauer
2Institut für Hochenergiephysik, Vienna, Austria
2,
J Brandstetter
J Brandstetter
2Institut für Hochenergiephysik, Vienna, Austria
2,
E Brondolin
E Brondolin
2Institut für Hochenergiephysik, Vienna, Austria
2,
M Dragicevic
M Dragicevic
2Institut für Hochenergiephysik, Vienna, Austria
2,
J Erö
J Erö
2Institut für Hochenergiephysik, Vienna, Austria
2,
A Escalante Del Valle
A Escalante Del Valle
2Institut für Hochenergiephysik, Vienna, Austria
2,
M Flechl
M Flechl
2Institut für Hochenergiephysik, Vienna, Austria
2,
R Frühwirth
R Frühwirth
2Institut für Hochenergiephysik, Vienna, Austria
2,
V M Ghete
V M Ghete
2Institut für Hochenergiephysik, Vienna, Austria
2,
J Hrubec
J Hrubec
2Institut für Hochenergiephysik, Vienna, Austria
2,
M Jeitler
M Jeitler
2Institut für Hochenergiephysik, Vienna, Austria
2,
N Krammer
N Krammer
2Institut für Hochenergiephysik, Vienna, Austria
2,
I Krätschmer
I Krätschmer
2Institut für Hochenergiephysik, Vienna, Austria
2,
D Liko
D Liko
2Institut für Hochenergiephysik, Vienna, Austria
2,
T Madlener
T Madlener
2Institut für Hochenergiephysik, Vienna, Austria
2,
I Mikulec
I Mikulec
2Institut für Hochenergiephysik, Vienna, Austria
2,
N Rad
N Rad
2Institut für Hochenergiephysik, Vienna, Austria
2,
H Rohringer
H Rohringer
2Institut für Hochenergiephysik, Vienna, Austria
2,
J Schieck
J Schieck
2Institut für Hochenergiephysik, Vienna, Austria
2,
R Schöfbeck
R Schöfbeck
2Institut für Hochenergiephysik, Vienna, Austria
2,
M Spanring
M Spanring
2Institut für Hochenergiephysik, Vienna, Austria
2,
D Spitzbart
D Spitzbart
2Institut für Hochenergiephysik, Vienna, Austria
2,
A Taurok
A Taurok
2Institut für Hochenergiephysik, Vienna, Austria
2,
W Waltenberger
W Waltenberger
2Institut für Hochenergiephysik, Vienna, Austria
2,
J Wittmann
J Wittmann
2Institut für Hochenergiephysik, Vienna, Austria
2,
C-E Wulz
C-E Wulz
2Institut für Hochenergiephysik, Vienna, Austria
2,
M Zarucki
M Zarucki
2Institut für Hochenergiephysik, Vienna, Austria
2,
V Chekhovsky
V Chekhovsky
3Institute for Nuclear Problems, Minsk, Belarus
3,
V Mossolov
V Mossolov
3Institute for Nuclear Problems, Minsk, Belarus
3,
J Suarez Gonzalez
J Suarez Gonzalez
3Institute for Nuclear Problems, Minsk, Belarus
3,
E A De Wolf
E A De Wolf
4Universiteit Antwerpen, Antwerp, Belgium
4,
D Di Croce
D Di Croce
4Universiteit Antwerpen, Antwerp, Belgium
4,
X Janssen
X Janssen
4Universiteit Antwerpen, Antwerp, Belgium
4,
J Lauwers
J Lauwers
4Universiteit Antwerpen, Antwerp, Belgium
4,
M Pieters
M Pieters
4Universiteit Antwerpen, Antwerp, Belgium
4,
M Van De Klundert
M Van De Klundert
4Universiteit Antwerpen, Antwerp, Belgium
4,
H Van Haevermaet
H Van Haevermaet
4Universiteit Antwerpen, Antwerp, Belgium
4,
P Van Mechelen
P Van Mechelen
4Universiteit Antwerpen, Antwerp, Belgium
4,
N Van Remortel
N Van Remortel
4Universiteit Antwerpen, Antwerp, Belgium
4,
S Abu Zeid
S Abu Zeid
5Vrije Universiteit Brussel, Brussels, Belgium
5,
F Blekman
F Blekman
5Vrije Universiteit Brussel, Brussels, Belgium
5,
J D’Hondt
J D’Hondt
5Vrije Universiteit Brussel, Brussels, Belgium
5,
I De Bruyn
I De Bruyn
5Vrije Universiteit Brussel, Brussels, Belgium
5,
J De Clercq
J De Clercq
5Vrije Universiteit Brussel, Brussels, Belgium
5,
K Deroover
K Deroover
5Vrije Universiteit Brussel, Brussels, Belgium
5,
G Flouris
G Flouris
5Vrije Universiteit Brussel, Brussels, Belgium
5,
D Lontkovskyi
D Lontkovskyi
5Vrije Universiteit Brussel, Brussels, Belgium
5,
S Lowette
S Lowette
5Vrije Universiteit Brussel, Brussels, Belgium
5,
I Marchesini
I Marchesini
5Vrije Universiteit Brussel, Brussels, Belgium
5,
S Moortgat
S Moortgat
5Vrije Universiteit Brussel, Brussels, Belgium
5,
L Moreels
L Moreels
5Vrije Universiteit Brussel, Brussels, Belgium
5,
Q Python
Q Python
5Vrije Universiteit Brussel, Brussels, Belgium
5,
K Skovpen
K Skovpen
5Vrije Universiteit Brussel, Brussels, Belgium
5,
S Tavernier
S Tavernier
5Vrije Universiteit Brussel, Brussels, Belgium
5,
W Van Doninck
W Van Doninck
5Vrije Universiteit Brussel, Brussels, Belgium
5,
P Van Mulders
P Van Mulders
5Vrije Universiteit Brussel, Brussels, Belgium
5,
I Van Parijs
I Van Parijs
5Vrije Universiteit Brussel, Brussels, Belgium
5,
D Beghin
D Beghin
6Université Libre de Bruxelles, Brussels, Belgium
6,
B Bilin
B Bilin
6Université Libre de Bruxelles, Brussels, Belgium
6,
H Brun
H Brun
6Université Libre de Bruxelles, Brussels, Belgium
6,
B Clerbaux
B Clerbaux
6Université Libre de Bruxelles, Brussels, Belgium
6,
G De Lentdecker
G De Lentdecker
6Université Libre de Bruxelles, Brussels, Belgium
6,
H Delannoy
H Delannoy
6Université Libre de Bruxelles, Brussels, Belgium
6,
B Dorney
B Dorney
6Université Libre de Bruxelles, Brussels, Belgium
6,
G Fasanella
G Fasanella
6Université Libre de Bruxelles, Brussels, Belgium
6,
L Favart
L Favart
6Université Libre de Bruxelles, Brussels, Belgium
6,
R Goldouzian
R Goldouzian
6Université Libre de Bruxelles, Brussels, Belgium
6,
A Grebenyuk
A Grebenyuk
6Université Libre de Bruxelles, Brussels, Belgium
6,
A K Kalsi
A K Kalsi
6Université Libre de Bruxelles, Brussels, Belgium
6,
T Lenzi
T Lenzi
6Université Libre de Bruxelles, Brussels, Belgium
6,
J Luetic
J Luetic
6Université Libre de Bruxelles, Brussels, Belgium
6,
N Postiau
N Postiau
6Université Libre de Bruxelles, Brussels, Belgium
6,
E Starling
E Starling
6Université Libre de Bruxelles, Brussels, Belgium
6,
L Thomas
L Thomas
6Université Libre de Bruxelles, Brussels, Belgium
6,
C Vander Velde
C Vander Velde
6Université Libre de Bruxelles, Brussels, Belgium
6,
P Vanlaer
P Vanlaer
6Université Libre de Bruxelles, Brussels, Belgium
6,
D Vannerom
D Vannerom
6Université Libre de Bruxelles, Brussels, Belgium
6,
Q Wang
Q Wang
6Université Libre de Bruxelles, Brussels, Belgium
6,
T Cornelis
T Cornelis
7Ghent University, Ghent, Belgium
7,
D Dobur
D Dobur
7Ghent University, Ghent, Belgium
7,
A Fagot
A Fagot
7Ghent University, Ghent, Belgium
7,
M Gul
M Gul
7Ghent University, Ghent, Belgium
7,
I Khvastunov
I Khvastunov
7Ghent University, Ghent, Belgium
7,
D Poyraz
D Poyraz
7Ghent University, Ghent, Belgium
7,
C Roskas
C Roskas
7Ghent University, Ghent, Belgium
7,
D Trocino
D Trocino
7Ghent University, Ghent, Belgium
7,
M Tytgat
M Tytgat
7Ghent University, Ghent, Belgium
7,
W Verbeke
W Verbeke
7Ghent University, Ghent, Belgium
7,
B Vermassen
B Vermassen
7Ghent University, Ghent, Belgium
7,
M Vit
M Vit
7Ghent University, Ghent, Belgium
7,
N Zaganidis
N Zaganidis
7Ghent University, Ghent, Belgium
7,
H Bakhshiansohi
H Bakhshiansohi
8Université Catholique de Louvain, Louvain-la-Neuve, Belgium
8,
O Bondu
O Bondu
8Université Catholique de Louvain, Louvain-la-Neuve, Belgium
8,
S Brochet
S Brochet
8Université Catholique de Louvain, Louvain-la-Neuve, Belgium
8,
G Bruno
G Bruno
8Université Catholique de Louvain, Louvain-la-Neuve, Belgium
8,
P David
P David
8Université Catholique de Louvain, Louvain-la-Neuve, Belgium
8,
C Delaere
C Delaere
8Université Catholique de Louvain, Louvain-la-Neuve, Belgium
8,
M Delcourt
M Delcourt
8Université Catholique de Louvain, Louvain-la-Neuve, Belgium
8,
B Francois
B Francois
8Université Catholique de Louvain, Louvain-la-Neuve, Belgium
8,
A Giammanco
A Giammanco
8Université Catholique de Louvain, Louvain-la-Neuve, Belgium
8,
G Krintiras
G Krintiras
8Université Catholique de Louvain, Louvain-la-Neuve, Belgium
8,
V Lemaitre
V Lemaitre
8Université Catholique de Louvain, Louvain-la-Neuve, Belgium
8,
A Magitteri
A Magitteri
8Université Catholique de Louvain, Louvain-la-Neuve, Belgium
8,
A Mertens
A Mertens
8Université Catholique de Louvain, Louvain-la-Neuve, Belgium
8,
M Musich
M Musich
8Université Catholique de Louvain, Louvain-la-Neuve, Belgium
8,
K Piotrzkowski
K Piotrzkowski
8Université Catholique de Louvain, Louvain-la-Neuve, Belgium
8,
A Saggio
A Saggio
8Université Catholique de Louvain, Louvain-la-Neuve, Belgium
8,
M Vidal Marono
M Vidal Marono
8Université Catholique de Louvain, Louvain-la-Neuve, Belgium
8,
S Wertz
S Wertz
8Université Catholique de Louvain, Louvain-la-Neuve, Belgium
8,
J Zobec
J Zobec
8Université Catholique de Louvain, Louvain-la-Neuve, Belgium
8,
F L Alves
F L Alves
9Centro Brasileiro de Pesquisas Fisicas, Rio de Janeiro, Brazil
9,
G A Alves
G A Alves
9Centro Brasileiro de Pesquisas Fisicas, Rio de Janeiro, Brazil
9,
L Brito
L Brito
9Centro Brasileiro de Pesquisas Fisicas, Rio de Janeiro, Brazil
9,
G Correia Silva
G Correia Silva
9Centro Brasileiro de Pesquisas Fisicas, Rio de Janeiro, Brazil
9,
C Hensel
C Hensel
9Centro Brasileiro de Pesquisas Fisicas, Rio de Janeiro, Brazil
9,
A Moraes
A Moraes
9Centro Brasileiro de Pesquisas Fisicas, Rio de Janeiro, Brazil
9,
M E Pol
M E Pol
9Centro Brasileiro de Pesquisas Fisicas, Rio de Janeiro, Brazil
9,
P Rebello Teles
P Rebello Teles
9Centro Brasileiro de Pesquisas Fisicas, Rio de Janeiro, Brazil
9,
E Belchior Batista Das Chagas
E Belchior Batista Das Chagas
10Universidade do Estado do Rio de Janeiro, Rio de Janeiro, Brazil
10,
W Carvalho
W Carvalho
10Universidade do Estado do Rio de Janeiro, Rio de Janeiro, Brazil
10,
J Chinellato
J Chinellato
10Universidade do Estado do Rio de Janeiro, Rio de Janeiro, Brazil
10,
E Coelho
E Coelho
10Universidade do Estado do Rio de Janeiro, Rio de Janeiro, Brazil
10,
E M Da Costa
E M Da Costa
10Universidade do Estado do Rio de Janeiro, Rio de Janeiro, Brazil
10,
G G Da Silveira
G G Da Silveira
10Universidade do Estado do Rio de Janeiro, Rio de Janeiro, Brazil
10,
D De Jesus Damiao
D De Jesus Damiao
10Universidade do Estado do Rio de Janeiro, Rio de Janeiro, Brazil
10,
C De Oliveira Martins
C De Oliveira Martins
10Universidade do Estado do Rio de Janeiro, Rio de Janeiro, Brazil
10,
S Fonseca De Souza
S Fonseca De Souza
10Universidade do Estado do Rio de Janeiro, Rio de Janeiro, Brazil
10,
H Malbouisson
H Malbouisson
10Universidade do Estado do Rio de Janeiro, Rio de Janeiro, Brazil
10,
D Matos Figueiredo
D Matos Figueiredo
10Universidade do Estado do Rio de Janeiro, Rio de Janeiro, Brazil
10,
M Melo De Almeida
M Melo De Almeida
10Universidade do Estado do Rio de Janeiro, Rio de Janeiro, Brazil
10,
C Mora Herrera
C Mora Herrera
10Universidade do Estado do Rio de Janeiro, Rio de Janeiro, Brazil
10,
L Mundim
L Mundim
10Universidade do Estado do Rio de Janeiro, Rio de Janeiro, Brazil
10,
H Nogima
H Nogima
10Universidade do Estado do Rio de Janeiro, Rio de Janeiro, Brazil
10,
W L Prado Da Silva
W L Prado Da Silva
10Universidade do Estado do Rio de Janeiro, Rio de Janeiro, Brazil
10,
L J Sanchez Rosas
L J Sanchez Rosas
10Universidade do Estado do Rio de Janeiro, Rio de Janeiro, Brazil
10,
A Santoro
A Santoro
10Universidade do Estado do Rio de Janeiro, Rio de Janeiro, Brazil
10,
A Sznajder
A Sznajder
10Universidade do Estado do Rio de Janeiro, Rio de Janeiro, Brazil
10,
M Thiel
M Thiel
10Universidade do Estado do Rio de Janeiro, Rio de Janeiro, Brazil
10,
E J Tonelli Manganote
E J Tonelli Manganote
10Universidade do Estado do Rio de Janeiro, Rio de Janeiro, Brazil
10,
F Torres Da Silva De Araujo
F Torres Da Silva De Araujo
10Universidade do Estado do Rio de Janeiro, Rio de Janeiro, Brazil
10,
A Vilela Pereira
A Vilela Pereira
10Universidade do Estado do Rio de Janeiro, Rio de Janeiro, Brazil
10,
S Ahuja
S Ahuja
11Universidade Estadual Paulista, Universidade Federal do ABC, São Paulo, Brazil
11,
C A Bernardes
C A Bernardes
11Universidade Estadual Paulista, Universidade Federal do ABC, São Paulo, Brazil
11,
L Calligaris
L Calligaris
11Universidade Estadual Paulista, Universidade Federal do ABC, São Paulo, Brazil
11,
T R Fernandez Perez Tomei
T R Fernandez Perez Tomei
11Universidade Estadual Paulista, Universidade Federal do ABC, São Paulo, Brazil
11,
E M Gregores
E M Gregores
11Universidade Estadual Paulista, Universidade Federal do ABC, São Paulo, Brazil
11,
P G Mercadante
P G Mercadante
11Universidade Estadual Paulista, Universidade Federal do ABC, São Paulo, Brazil
11,
S F Novaes
S F Novaes
11Universidade Estadual Paulista, Universidade Federal do ABC, São Paulo, Brazil
11,
SandraS Padula
SandraS Padula
11Universidade Estadual Paulista, Universidade Federal do ABC, São Paulo, Brazil
11,
D Romero Abad
D Romero Abad
11Universidade Estadual Paulista, Universidade Federal do ABC, São Paulo, Brazil
11,
A Aleksandrov
A Aleksandrov
12Institute for Nuclear Research and Nuclear Energy, Bulgarian Academy of Sciences, Sofia, Bulgaria
12,
R Hadjiiska
R Hadjiiska
12Institute for Nuclear Research and Nuclear Energy, Bulgarian Academy of Sciences, Sofia, Bulgaria
12,
P Iaydjiev
P Iaydjiev
12Institute for Nuclear Research and Nuclear Energy, Bulgarian Academy of Sciences, Sofia, Bulgaria
12,
A Marinov
A Marinov
12Institute for Nuclear Research and Nuclear Energy, Bulgarian Academy of Sciences, Sofia, Bulgaria
12,
M Misheva
M Misheva
12Institute for Nuclear Research and Nuclear Energy, Bulgarian Academy of Sciences, Sofia, Bulgaria
12,
M Rodozov
M Rodozov
12Institute for Nuclear Research and Nuclear Energy, Bulgarian Academy of Sciences, Sofia, Bulgaria
12,
M Shopova
M Shopova
12Institute for Nuclear Research and Nuclear Energy, Bulgarian Academy of Sciences, Sofia, Bulgaria
12,
G Sultanov
G Sultanov
12Institute for Nuclear Research and Nuclear Energy, Bulgarian Academy of Sciences, Sofia, Bulgaria
12,
A Dimitrov
A Dimitrov
13University of Sofia, Sofia, Bulgaria
13,
L Litov
L Litov
13University of Sofia, Sofia, Bulgaria
13,
B Pavlov
B Pavlov
13University of Sofia, Sofia, Bulgaria
13,
P Petkov
P Petkov
13University of Sofia, Sofia, Bulgaria
13,
W Fang
W Fang
14Beihang University, Beijing, China
14,
X Gao
X Gao
14Beihang University, Beijing, China
14,
L Yuan
L Yuan
14Beihang University, Beijing, China
14,
M Ahmad
M Ahmad
15Institute of High Energy Physics, Beijing, China
15,
J G Bian
J G Bian
15Institute of High Energy Physics, Beijing, China
15,
G M Chen
G M Chen
15Institute of High Energy Physics, Beijing, China
15,
H S Chen
H S Chen
15Institute of High Energy Physics, Beijing, China
15,
M Chen
M Chen
15Institute of High Energy Physics, Beijing, China
15,
Y Chen
Y Chen
15Institute of High Energy Physics, Beijing, China
15,
C H Jiang
C H Jiang
15Institute of High Energy Physics, Beijing, China
15,
D Leggat
D Leggat
15Institute of High Energy Physics, Beijing, China
15,
H Liao
H Liao
15Institute of High Energy Physics, Beijing, China
15,
Z Liu
Z Liu
15Institute of High Energy Physics, Beijing, China
15,
F Romeo
F Romeo
15Institute of High Energy Physics, Beijing, China
15,
S M Shaheen
S M Shaheen
15Institute of High Energy Physics, Beijing, China
15,
A Spiezia
A Spiezia
15Institute of High Energy Physics, Beijing, China
15,
J Tao
J Tao
15Institute of High Energy Physics, Beijing, China
15,
C Wang
C Wang
15Institute of High Energy Physics, Beijing, China
15,
Z Wang
Z Wang
15Institute of High Energy Physics, Beijing, China
15,
E Yazgan
E Yazgan
15Institute of High Energy Physics, Beijing, China
15,
H Zhang
H Zhang
15Institute of High Energy Physics, Beijing, China
15,
J Zhao
J Zhao
15Institute of High Energy Physics, Beijing, China
15,
Y Ban
Y Ban
16State Key Laboratory of Nuclear Physics and Technology, Peking University, Beijing, China
16,
G Chen
G Chen
16State Key Laboratory of Nuclear Physics and Technology, Peking University, Beijing, China
16,
A Levin
A Levin
16State Key Laboratory of Nuclear Physics and Technology, Peking University, Beijing, China
16,
J Li
J Li
16State Key Laboratory of Nuclear Physics and Technology, Peking University, Beijing, China
16,
L Li
L Li
16State Key Laboratory of Nuclear Physics and Technology, Peking University, Beijing, China
16,
Q Li
Q Li
16State Key Laboratory of Nuclear Physics and Technology, Peking University, Beijing, China
16,
Y Mao
Y Mao
16State Key Laboratory of Nuclear Physics and Technology, Peking University, Beijing, China
16,
S J Qian
S J Qian
16State Key Laboratory of Nuclear Physics and Technology, Peking University, Beijing, China
16,
D Wang
D Wang
16State Key Laboratory of Nuclear Physics and Technology, Peking University, Beijing, China
16,
Z Xu
Z Xu
16State Key Laboratory of Nuclear Physics and Technology, Peking University, Beijing, China
16,
Y Wang
Y Wang
17Tsinghua University, Beijing, China
17,
C Avila
C Avila
18Universidad de Los Andes, Bogotá, Colombia
18,
A Cabrera
A Cabrera
18Universidad de Los Andes, Bogotá, Colombia
18,
C A Carrillo Montoya
C A Carrillo Montoya
18Universidad de Los Andes, Bogotá, Colombia
18,
L F Chaparro Sierra
L F Chaparro Sierra
18Universidad de Los Andes, Bogotá, Colombia
18,
C Florez
C Florez
18Universidad de Los Andes, Bogotá, Colombia
18,
C F González Hernández
C F González Hernández
18Universidad de Los Andes, Bogotá, Colombia
18,
M A Segura Delgado
M A Segura Delgado
18Universidad de Los Andes, Bogotá, Colombia
18,
B Courbon
B Courbon
19University of Split, Faculty of Electrical Engineering, Mechanical Engineering and Naval Architecture, Split, Croatia
19,
N Godinovic
N Godinovic
19University of Split, Faculty of Electrical Engineering, Mechanical Engineering and Naval Architecture, Split, Croatia
19,
D Lelas
D Lelas
19University of Split, Faculty of Electrical Engineering, Mechanical Engineering and Naval Architecture, Split, Croatia
19,
I Puljak
I Puljak
19University of Split, Faculty of Electrical Engineering, Mechanical Engineering and Naval Architecture, Split, Croatia
19,
T Sculac
T Sculac
19University of Split, Faculty of Electrical Engineering, Mechanical Engineering and Naval Architecture, Split, Croatia
19,
Z Antunovic
Z Antunovic
20University of Split, Faculty of Science, Split, Croatia
20,
M Kovac
M Kovac
20University of Split, Faculty of Science, Split, Croatia
20,
V Brigljevic
V Brigljevic
21Institute Rudjer Boskovic, Zagreb, Croatia
21,
D Ferencek
D Ferencek
21Institute Rudjer Boskovic, Zagreb, Croatia
21,
K Kadija
K Kadija
21Institute Rudjer Boskovic, Zagreb, Croatia
21,
B Mesic
B Mesic
21Institute Rudjer Boskovic, Zagreb, Croatia
21,
A Starodumov
A Starodumov
21Institute Rudjer Boskovic, Zagreb, Croatia
21,
T Susa
T Susa
21Institute Rudjer Boskovic, Zagreb, Croatia
21,
M W Ather
M W Ather
22University of Cyprus, Nicosia, Cyprus
22,
A Attikis
A Attikis
22University of Cyprus, Nicosia, Cyprus
22,
G Mavromanolakis
G Mavromanolakis
22University of Cyprus, Nicosia, Cyprus
22,
J Mousa
J Mousa
22University of Cyprus, Nicosia, Cyprus
22,
C Nicolaou
C Nicolaou
22University of Cyprus, Nicosia, Cyprus
22,
F Ptochos
F Ptochos
22University of Cyprus, Nicosia, Cyprus
22,
P A Razis
P A Razis
22University of Cyprus, Nicosia, Cyprus
22,
H Rykaczewski
H Rykaczewski
22University of Cyprus, Nicosia, Cyprus
22,
M Finger
M Finger
23Charles University, Prague, Czech Republic
23,
M Finger Jr
M Finger Jr
23Charles University, Prague, Czech Republic
23,
E Ayala
E Ayala
24Escuela Politecnica Nacional, Quito, Ecuador
24,
E Carrera Jarrin
E Carrera Jarrin
25Universidad San Francisco de Quito, Quito, Ecuador
25,
H Abdalla
H Abdalla
26Academy of Scientific Research and Technology of the Arab Republic of Egypt, Egyptian Network of High Energy Physics, Cairo, Egypt
26,
A A Abdelalim
A A Abdelalim
26Academy of Scientific Research and Technology of the Arab Republic of Egypt, Egyptian Network of High Energy Physics, Cairo, Egypt
26,
A Mohamed
A Mohamed
26Academy of Scientific Research and Technology of the Arab Republic of Egypt, Egyptian Network of High Energy Physics, Cairo, Egypt
26,
A Carvalho Antunes De Oliveira
A Carvalho Antunes De Oliveira
27National Institute of Chemical Physics and Biophysics, Tallinn, Estonia
27,
R K Dewanjee
R K Dewanjee
27National Institute of Chemical Physics and Biophysics, Tallinn, Estonia
27,
K Ehataht
K Ehataht
27National Institute of Chemical Physics and Biophysics, Tallinn, Estonia
27,
M Kadastik
M Kadastik
27National Institute of Chemical Physics and Biophysics, Tallinn, Estonia
27,
M Raidal
M Raidal
27National Institute of Chemical Physics and Biophysics, Tallinn, Estonia
27,
C Veelken
C Veelken
27National Institute of Chemical Physics and Biophysics, Tallinn, Estonia
27,
P Eerola
P Eerola
28Department of Physics, University of Helsinki, Helsinki, Finland
28,
H Kirschenmann
H Kirschenmann
28Department of Physics, University of Helsinki, Helsinki, Finland
28,
J Pekkanen
J Pekkanen
28Department of Physics, University of Helsinki, Helsinki, Finland
28,
M Voutilainen
M Voutilainen
28Department of Physics, University of Helsinki, Helsinki, Finland
28,
J Havukainen
J Havukainen
29Helsinki Institute of Physics, Helsinki, Finland
29,
J K Heikkilä
J K Heikkilä
29Helsinki Institute of Physics, Helsinki, Finland
29,
T Järvinen
T Järvinen
29Helsinki Institute of Physics, Helsinki, Finland
29,
V Karimäki
V Karimäki
29Helsinki Institute of Physics, Helsinki, Finland
29,
R Kinnunen
R Kinnunen
29Helsinki Institute of Physics, Helsinki, Finland
29,
T Lampén
T Lampén
29Helsinki Institute of Physics, Helsinki, Finland
29,
K Lassila-Perini
K Lassila-Perini
29Helsinki Institute of Physics, Helsinki, Finland
29,
S Laurila
S Laurila
29Helsinki Institute of Physics, Helsinki, Finland
29,
S Lehti
S Lehti
29Helsinki Institute of Physics, Helsinki, Finland
29,
T Lindén
T Lindén
29Helsinki Institute of Physics, Helsinki, Finland
29,
P Luukka
P Luukka
29Helsinki Institute of Physics, Helsinki, Finland
29,
T Mäenpää
T Mäenpää
29Helsinki Institute of Physics, Helsinki, Finland
29,
H Siikonen
H Siikonen
29Helsinki Institute of Physics, Helsinki, Finland
29,
E Tuominen
E Tuominen
29Helsinki Institute of Physics, Helsinki, Finland
29,
J Tuominiemi
J Tuominiemi
29Helsinki Institute of Physics, Helsinki, Finland
29,
T Tuuva
T Tuuva
30Lappeenranta University of Technology, Lappeenranta, Finland
30,
M Besancon
M Besancon
31IRFU, CEA, Université Paris-Saclay, Gif-sur-Yvette, France
31,
F Couderc
F Couderc
31IRFU, CEA, Université Paris-Saclay, Gif-sur-Yvette, France
31,
M Dejardin
M Dejardin
31IRFU, CEA, Université Paris-Saclay, Gif-sur-Yvette, France
31,
D Denegri
D Denegri
31IRFU, CEA, Université Paris-Saclay, Gif-sur-Yvette, France
31,
J L Faure
J L Faure
31IRFU, CEA, Université Paris-Saclay, Gif-sur-Yvette, France
31,
F Ferri
F Ferri
31IRFU, CEA, Université Paris-Saclay, Gif-sur-Yvette, France
31,
S Ganjour
S Ganjour
31IRFU, CEA, Université Paris-Saclay, Gif-sur-Yvette, France
31,
A Givernaud
A Givernaud
31IRFU, CEA, Université Paris-Saclay, Gif-sur-Yvette, France
31,
P Gras
P Gras
31IRFU, CEA, Université Paris-Saclay, Gif-sur-Yvette, France
31,
G Hamel de Monchenault
G Hamel de Monchenault
31IRFU, CEA, Université Paris-Saclay, Gif-sur-Yvette, France
31,
P Jarry
P Jarry
31IRFU, CEA, Université Paris-Saclay, Gif-sur-Yvette, France
31,
C Leloup
C Leloup
31IRFU, CEA, Université Paris-Saclay, Gif-sur-Yvette, France
31,
E Locci
E Locci
31IRFU, CEA, Université Paris-Saclay, Gif-sur-Yvette, France
31,
J Malcles
J Malcles
31IRFU, CEA, Université Paris-Saclay, Gif-sur-Yvette, France
31,
G Negro
G Negro
31IRFU, CEA, Université Paris-Saclay, Gif-sur-Yvette, France
31,
J Rander
J Rander
31IRFU, CEA, Université Paris-Saclay, Gif-sur-Yvette, France
31,
A Rosowsky
A Rosowsky
31IRFU, CEA, Université Paris-Saclay, Gif-sur-Yvette, France
31,
M Ö Sahin
M Ö Sahin
31IRFU, CEA, Université Paris-Saclay, Gif-sur-Yvette, France
31,
M Titov
M Titov
31IRFU, CEA, Université Paris-Saclay, Gif-sur-Yvette, France
31,
A Abdulsalam
A Abdulsalam
32Laboratoire Leprince-Ringuet, Ecole polytechnique, CNRS/IN2P3, Université Paris-Saclay, Palaiseau, France
32,
C Amendola
C Amendola
32Laboratoire Leprince-Ringuet, Ecole polytechnique, CNRS/IN2P3, Université Paris-Saclay, Palaiseau, France
32,
I Antropov
I Antropov
32Laboratoire Leprince-Ringuet, Ecole polytechnique, CNRS/IN2P3, Université Paris-Saclay, Palaiseau, France
32,
F Beaudette
F Beaudette
32Laboratoire Leprince-Ringuet, Ecole polytechnique, CNRS/IN2P3, Université Paris-Saclay, Palaiseau, France
32,
P Busson
P Busson
32Laboratoire Leprince-Ringuet, Ecole polytechnique, CNRS/IN2P3, Université Paris-Saclay, Palaiseau, France
32,
C Charlot
C Charlot
32Laboratoire Leprince-Ringuet, Ecole polytechnique, CNRS/IN2P3, Université Paris-Saclay, Palaiseau, France
32,
R Granier de Cassagnac
R Granier de Cassagnac
32Laboratoire Leprince-Ringuet, Ecole polytechnique, CNRS/IN2P3, Université Paris-Saclay, Palaiseau, France
32,
I Kucher
I Kucher
32Laboratoire Leprince-Ringuet, Ecole polytechnique, CNRS/IN2P3, Université Paris-Saclay, Palaiseau, France
32,
S Lisniak
S Lisniak
32Laboratoire Leprince-Ringuet, Ecole polytechnique, CNRS/IN2P3, Université Paris-Saclay, Palaiseau, France
32,
A Lobanov
A Lobanov
32Laboratoire Leprince-Ringuet, Ecole polytechnique, CNRS/IN2P3, Université Paris-Saclay, Palaiseau, France
32,
J Martin Perez
J Martin Perez
32Laboratoire Leprince-Ringuet, Ecole polytechnique, CNRS/IN2P3, Université Paris-Saclay, Palaiseau, France
32,
M Nguyen
M Nguyen
32Laboratoire Leprince-Ringuet, Ecole polytechnique, CNRS/IN2P3, Université Paris-Saclay, Palaiseau, France
32,
C Ochando
C Ochando
32Laboratoire Leprince-Ringuet, Ecole polytechnique, CNRS/IN2P3, Université Paris-Saclay, Palaiseau, France
32,
G Ortona
G Ortona
32Laboratoire Leprince-Ringuet, Ecole polytechnique, CNRS/IN2P3, Université Paris-Saclay, Palaiseau, France
32,
P Pigard
P Pigard
32Laboratoire Leprince-Ringuet, Ecole polytechnique, CNRS/IN2P3, Université Paris-Saclay, Palaiseau, France
32,
R Salerno
R Salerno
32Laboratoire Leprince-Ringuet, Ecole polytechnique, CNRS/IN2P3, Université Paris-Saclay, Palaiseau, France
32,
J B Sauvan
J B Sauvan
32Laboratoire Leprince-Ringuet, Ecole polytechnique, CNRS/IN2P3, Université Paris-Saclay, Palaiseau, France
32,
Y Sirois
Y Sirois
32Laboratoire Leprince-Ringuet, Ecole polytechnique, CNRS/IN2P3, Université Paris-Saclay, Palaiseau, France
32,
A G Stahl Leiton
A G Stahl Leiton
32Laboratoire Leprince-Ringuet, Ecole polytechnique, CNRS/IN2P3, Université Paris-Saclay, Palaiseau, France
32,
A Zabi
A Zabi
32Laboratoire Leprince-Ringuet, Ecole polytechnique, CNRS/IN2P3, Université Paris-Saclay, Palaiseau, France
32,
A Zghiche
A Zghiche
32Laboratoire Leprince-Ringuet, Ecole polytechnique, CNRS/IN2P3, Université Paris-Saclay, Palaiseau, France
32,
J-L Agram
J-L Agram
33Université de Strasbourg, CNRS, IPHC UMR 7178, Strasbourg, France
33,
J Andrea
J Andrea
33Université de Strasbourg, CNRS, IPHC UMR 7178, Strasbourg, France
33,
D Bloch
D Bloch
33Université de Strasbourg, CNRS, IPHC UMR 7178, Strasbourg, France
33,
J-M Brom
J-M Brom
33Université de Strasbourg, CNRS, IPHC UMR 7178, Strasbourg, France
33,
E C Chabert
E C Chabert
33Université de Strasbourg, CNRS, IPHC UMR 7178, Strasbourg, France
33,
V Cherepanov
V Cherepanov
33Université de Strasbourg, CNRS, IPHC UMR 7178, Strasbourg, France
33,
C Collard
C Collard
33Université de Strasbourg, CNRS, IPHC UMR 7178, Strasbourg, France
33,
E Conte
E Conte
33Université de Strasbourg, CNRS, IPHC UMR 7178, Strasbourg, France
33,
J-C Fontaine
J-C Fontaine
33Université de Strasbourg, CNRS, IPHC UMR 7178, Strasbourg, France
33,
D Gelé
D Gelé
33Université de Strasbourg, CNRS, IPHC UMR 7178, Strasbourg, France
33,
U Goerlach
U Goerlach
33Université de Strasbourg, CNRS, IPHC UMR 7178, Strasbourg, France
33,
M Jansová
M Jansová
33Université de Strasbourg, CNRS, IPHC UMR 7178, Strasbourg, France
33,
A-C Le Bihan
A-C Le Bihan
33Université de Strasbourg, CNRS, IPHC UMR 7178, Strasbourg, France
33,
N Tonon
N Tonon
33Université de Strasbourg, CNRS, IPHC UMR 7178, Strasbourg, France
33,
P Van Hove
P Van Hove
33Université de Strasbourg, CNRS, IPHC UMR 7178, Strasbourg, France
33,
S Gadrat
S Gadrat
34Centre de Calcul de l’Institut National de Physique Nucleaire et de Physique des Particules, CNRS/IN2P3, Villeurbanne, France
34,
S Beauceron
S Beauceron
35Université de Lyon, Université Claude Bernard Lyon 1, CNRS-IN2P3, Institut de Physique Nucléaire de Lyon, Villeurbanne, France
35,
C Bernet
C Bernet
35Université de Lyon, Université Claude Bernard Lyon 1, CNRS-IN2P3, Institut de Physique Nucléaire de Lyon, Villeurbanne, France
35,
G Boudoul
G Boudoul
35Université de Lyon, Université Claude Bernard Lyon 1, CNRS-IN2P3, Institut de Physique Nucléaire de Lyon, Villeurbanne, France
35,
N Chanon
N Chanon
35Université de Lyon, Université Claude Bernard Lyon 1, CNRS-IN2P3, Institut de Physique Nucléaire de Lyon, Villeurbanne, France
35,
R Chierici
R Chierici
35Université de Lyon, Université Claude Bernard Lyon 1, CNRS-IN2P3, Institut de Physique Nucléaire de Lyon, Villeurbanne, France
35,
D Contardo
D Contardo
35Université de Lyon, Université Claude Bernard Lyon 1, CNRS-IN2P3, Institut de Physique Nucléaire de Lyon, Villeurbanne, France
35,
P Depasse
P Depasse
35Université de Lyon, Université Claude Bernard Lyon 1, CNRS-IN2P3, Institut de Physique Nucléaire de Lyon, Villeurbanne, France
35,
H El Mamouni
H El Mamouni
35Université de Lyon, Université Claude Bernard Lyon 1, CNRS-IN2P3, Institut de Physique Nucléaire de Lyon, Villeurbanne, France
35,
J Fay
J Fay
35Université de Lyon, Université Claude Bernard Lyon 1, CNRS-IN2P3, Institut de Physique Nucléaire de Lyon, Villeurbanne, France
35,
L Finco
L Finco
35Université de Lyon, Université Claude Bernard Lyon 1, CNRS-IN2P3, Institut de Physique Nucléaire de Lyon, Villeurbanne, France
35,
S Gascon
S Gascon
35Université de Lyon, Université Claude Bernard Lyon 1, CNRS-IN2P3, Institut de Physique Nucléaire de Lyon, Villeurbanne, France
35,
M Gouzevitch
M Gouzevitch
35Université de Lyon, Université Claude Bernard Lyon 1, CNRS-IN2P3, Institut de Physique Nucléaire de Lyon, Villeurbanne, France
35,
G Grenier
G Grenier
35Université de Lyon, Université Claude Bernard Lyon 1, CNRS-IN2P3, Institut de Physique Nucléaire de Lyon, Villeurbanne, France
35,
B Ille
B Ille
35Université de Lyon, Université Claude Bernard Lyon 1, CNRS-IN2P3, Institut de Physique Nucléaire de Lyon, Villeurbanne, France
35,
F Lagarde
F Lagarde
35Université de Lyon, Université Claude Bernard Lyon 1, CNRS-IN2P3, Institut de Physique Nucléaire de Lyon, Villeurbanne, France
35,
I B Laktineh
I B Laktineh
35Université de Lyon, Université Claude Bernard Lyon 1, CNRS-IN2P3, Institut de Physique Nucléaire de Lyon, Villeurbanne, France
35,
H Lattaud
H Lattaud
35Université de Lyon, Université Claude Bernard Lyon 1, CNRS-IN2P3, Institut de Physique Nucléaire de Lyon, Villeurbanne, France
35,
M Lethuillier
M Lethuillier
35Université de Lyon, Université Claude Bernard Lyon 1, CNRS-IN2P3, Institut de Physique Nucléaire de Lyon, Villeurbanne, France
35,
L Mirabito
L Mirabito
35Université de Lyon, Université Claude Bernard Lyon 1, CNRS-IN2P3, Institut de Physique Nucléaire de Lyon, Villeurbanne, France
35,
A L Pequegnot
A L Pequegnot
35Université de Lyon, Université Claude Bernard Lyon 1, CNRS-IN2P3, Institut de Physique Nucléaire de Lyon, Villeurbanne, France
35,
S Perries
S Perries
35Université de Lyon, Université Claude Bernard Lyon 1, CNRS-IN2P3, Institut de Physique Nucléaire de Lyon, Villeurbanne, France
35,
A Popov
A Popov
35Université de Lyon, Université Claude Bernard Lyon 1, CNRS-IN2P3, Institut de Physique Nucléaire de Lyon, Villeurbanne, France
35,
V Sordini
V Sordini
35Université de Lyon, Université Claude Bernard Lyon 1, CNRS-IN2P3, Institut de Physique Nucléaire de Lyon, Villeurbanne, France
35,
M Vander Donckt
M Vander Donckt
35Université de Lyon, Université Claude Bernard Lyon 1, CNRS-IN2P3, Institut de Physique Nucléaire de Lyon, Villeurbanne, France
35,
S Viret
S Viret
35Université de Lyon, Université Claude Bernard Lyon 1, CNRS-IN2P3, Institut de Physique Nucléaire de Lyon, Villeurbanne, France
35,
S Zhang
S Zhang
35Université de Lyon, Université Claude Bernard Lyon 1, CNRS-IN2P3, Institut de Physique Nucléaire de Lyon, Villeurbanne, France
35,
A Khvedelidze
A Khvedelidze
36Georgian Technical University, Tbilisi, Georgia
36,
D Lomidze
D Lomidze
37Tbilisi State University, Tbilisi, Georgia
37,
C Autermann
C Autermann
38RWTH Aachen University, I. Physikalisches Institut, Aachen, Germany
38,
L Feld
L Feld
38RWTH Aachen University, I. Physikalisches Institut, Aachen, Germany
38,
M K Kiesel
M K Kiesel
38RWTH Aachen University, I. Physikalisches Institut, Aachen, Germany
38,
K Klein
K Klein
38RWTH Aachen University, I. Physikalisches Institut, Aachen, Germany
38,
M Lipinski
M Lipinski
38RWTH Aachen University, I. Physikalisches Institut, Aachen, Germany
38,
M Preuten
M Preuten
38RWTH Aachen University, I. Physikalisches Institut, Aachen, Germany
38,
M P Rauch
M P Rauch
38RWTH Aachen University, I. Physikalisches Institut, Aachen, Germany
38,
C Schomakers
C Schomakers
38RWTH Aachen University, I. Physikalisches Institut, Aachen, Germany
38,
J Schulz
J Schulz
38RWTH Aachen University, I. Physikalisches Institut, Aachen, Germany
38,
M Teroerde
M Teroerde
38RWTH Aachen University, I. Physikalisches Institut, Aachen, Germany
38,
B Wittmer
B Wittmer
38RWTH Aachen University, I. Physikalisches Institut, Aachen, Germany
38,
V Zhukov
V Zhukov
38RWTH Aachen University, I. Physikalisches Institut, Aachen, Germany
38,
A Albert
A Albert
39RWTH Aachen University, III. Physikalisches Institut A, Aachen, Germany
39,
D Duchardt
D Duchardt
39RWTH Aachen University, III. Physikalisches Institut A, Aachen, Germany
39,
M Endres
M Endres
39RWTH Aachen University, III. Physikalisches Institut A, Aachen, Germany
39,
M Erdmann
M Erdmann
39RWTH Aachen University, III. Physikalisches Institut A, Aachen, Germany
39,
T Esch
T Esch
39RWTH Aachen University, III. Physikalisches Institut A, Aachen, Germany
39,
R Fischer
R Fischer
39RWTH Aachen University, III. Physikalisches Institut A, Aachen, Germany
39,
S Ghosh
S Ghosh
39RWTH Aachen University, III. Physikalisches Institut A, Aachen, Germany
39,
A Güth
A Güth
39RWTH Aachen University, III. Physikalisches Institut A, Aachen, Germany
39,
T Hebbeker
T Hebbeker
39RWTH Aachen University, III. Physikalisches Institut A, Aachen, Germany
39,
C Heidemann
C Heidemann
39RWTH Aachen University, III. Physikalisches Institut A, Aachen, Germany
39,
K Hoepfner
K Hoepfner
39RWTH Aachen University, III. Physikalisches Institut A, Aachen, Germany
39,
H Keller
H Keller
39RWTH Aachen University, III. Physikalisches Institut A, Aachen, Germany
39,
S Knutzen
S Knutzen
39RWTH Aachen University, III. Physikalisches Institut A, Aachen, Germany
39,
L Mastrolorenzo
L Mastrolorenzo
39RWTH Aachen University, III. Physikalisches Institut A, Aachen, Germany
39,
M Merschmeyer
M Merschmeyer
39RWTH Aachen University, III. Physikalisches Institut A, Aachen, Germany
39,
A Meyer
A Meyer
39RWTH Aachen University, III. Physikalisches Institut A, Aachen, Germany
39,
P Millet
P Millet
39RWTH Aachen University, III. Physikalisches Institut A, Aachen, Germany
39,
S Mukherjee
S Mukherjee
39RWTH Aachen University, III. Physikalisches Institut A, Aachen, Germany
39,
T Pook
T Pook
39RWTH Aachen University, III. Physikalisches Institut A, Aachen, Germany
39,
M Radziej
M Radziej
39RWTH Aachen University, III. Physikalisches Institut A, Aachen, Germany
39,
H Reithler
H Reithler
39RWTH Aachen University, III. Physikalisches Institut A, Aachen, Germany
39,
M Rieger
M Rieger
39RWTH Aachen University, III. Physikalisches Institut A, Aachen, Germany
39,
F Scheuch
F Scheuch
39RWTH Aachen University, III. Physikalisches Institut A, Aachen, Germany
39,
A Schmidt
A Schmidt
39RWTH Aachen University, III. Physikalisches Institut A, Aachen, Germany
39,
D Teyssier
D Teyssier
39RWTH Aachen University, III. Physikalisches Institut A, Aachen, Germany
39,
G Flügge
G Flügge
40RWTH Aachen University, III. Physikalisches Institut B, Aachen, Germany
40,
O Hlushchenko
O Hlushchenko
40RWTH Aachen University, III. Physikalisches Institut B, Aachen, Germany
40,
B Kargoll
B Kargoll
40RWTH Aachen University, III. Physikalisches Institut B, Aachen, Germany
40,
T Kress
T Kress
40RWTH Aachen University, III. Physikalisches Institut B, Aachen, Germany
40,
A Künsken
A Künsken
40RWTH Aachen University, III. Physikalisches Institut B, Aachen, Germany
40,
T Müller
T Müller
40RWTH Aachen University, III. Physikalisches Institut B, Aachen, Germany
40,
A Nehrkorn
A Nehrkorn
40RWTH Aachen University, III. Physikalisches Institut B, Aachen, Germany
40,
A Nowack
A Nowack
40RWTH Aachen University, III. Physikalisches Institut B, Aachen, Germany
40,
C Pistone
C Pistone
40RWTH Aachen University, III. Physikalisches Institut B, Aachen, Germany
40,
O Pooth
O Pooth
40RWTH Aachen University, III. Physikalisches Institut B, Aachen, Germany
40,
H Sert
H Sert
40RWTH Aachen University, III. Physikalisches Institut B, Aachen, Germany
40,
A Stahl
A Stahl
40RWTH Aachen University, III. Physikalisches Institut B, Aachen, Germany
40,
M Aldaya Martin
M Aldaya Martin
41Deutsches Elektronen-Synchrotron, Hamburg, Germany
41,
T Arndt
T Arndt
41Deutsches Elektronen-Synchrotron, Hamburg, Germany
41,
C Asawatangtrakuldee
C Asawatangtrakuldee
41Deutsches Elektronen-Synchrotron, Hamburg, Germany
41,
I Babounikau
I Babounikau
41Deutsches Elektronen-Synchrotron, Hamburg, Germany
41,
K Beernaert
K Beernaert
41Deutsches Elektronen-Synchrotron, Hamburg, Germany
41,
O Behnke
O Behnke
41Deutsches Elektronen-Synchrotron, Hamburg, Germany
41,
U Behrens
U Behrens
41Deutsches Elektronen-Synchrotron, Hamburg, Germany
41,
A Bermúdez Martínez
A Bermúdez Martínez
41Deutsches Elektronen-Synchrotron, Hamburg, Germany
41,
D Bertsche
D Bertsche
41Deutsches Elektronen-Synchrotron, Hamburg, Germany
41,
A A Bin Anuar
A A Bin Anuar
41Deutsches Elektronen-Synchrotron, Hamburg, Germany
41,
K Borras
K Borras
41Deutsches Elektronen-Synchrotron, Hamburg, Germany
41,
V Botta
V Botta
41Deutsches Elektronen-Synchrotron, Hamburg, Germany
41,
A Campbell
A Campbell
41Deutsches Elektronen-Synchrotron, Hamburg, Germany
41,
P Connor
P Connor
41Deutsches Elektronen-Synchrotron, Hamburg, Germany
41,
C Contreras-Campana
C Contreras-Campana
41Deutsches Elektronen-Synchrotron, Hamburg, Germany
41,
F Costanza
F Costanza
41Deutsches Elektronen-Synchrotron, Hamburg, Germany
41,
V Danilov
V Danilov
41Deutsches Elektronen-Synchrotron, Hamburg, Germany
41,
A De Wit
A De Wit
41Deutsches Elektronen-Synchrotron, Hamburg, Germany
41,
M M Defranchis
M M Defranchis
41Deutsches Elektronen-Synchrotron, Hamburg, Germany
41,
C Diez Pardos
C Diez Pardos
41Deutsches Elektronen-Synchrotron, Hamburg, Germany
41,
D Domínguez Damiani
D Domínguez Damiani
41Deutsches Elektronen-Synchrotron, Hamburg, Germany
41,
G Eckerlin
G Eckerlin
41Deutsches Elektronen-Synchrotron, Hamburg, Germany
41,
T Eichhorn
T Eichhorn
41Deutsches Elektronen-Synchrotron, Hamburg, Germany
41,
A Elwood
A Elwood
41Deutsches Elektronen-Synchrotron, Hamburg, Germany
41,
E Eren
E Eren
41Deutsches Elektronen-Synchrotron, Hamburg, Germany
41,
E Gallo
E Gallo
41Deutsches Elektronen-Synchrotron, Hamburg, Germany
41,
A Geiser
A Geiser
41Deutsches Elektronen-Synchrotron, Hamburg, Germany
41,
J M Grados Luyando
J M Grados Luyando
41Deutsches Elektronen-Synchrotron, Hamburg, Germany
41,
A Grohsjean
A Grohsjean
41Deutsches Elektronen-Synchrotron, Hamburg, Germany
41,
P Gunnellini
P Gunnellini
41Deutsches Elektronen-Synchrotron, Hamburg, Germany
41,
M Guthoff
M Guthoff
41Deutsches Elektronen-Synchrotron, Hamburg, Germany
41,
M Haranko
M Haranko
41Deutsches Elektronen-Synchrotron, Hamburg, Germany
41,
A Harb
A Harb
41Deutsches Elektronen-Synchrotron, Hamburg, Germany
41,
J Hauk
J Hauk
41Deutsches Elektronen-Synchrotron, Hamburg, Germany
41,
H Jung
H Jung
41Deutsches Elektronen-Synchrotron, Hamburg, Germany
41,
M Kasemann
M Kasemann
41Deutsches Elektronen-Synchrotron, Hamburg, Germany
41,
J Keaveney
J Keaveney
41Deutsches Elektronen-Synchrotron, Hamburg, Germany
41,
C Kleinwort
C Kleinwort
41Deutsches Elektronen-Synchrotron, Hamburg, Germany
41,
J Knolle
J Knolle
41Deutsches Elektronen-Synchrotron, Hamburg, Germany
41,
D Krücker
D Krücker
41Deutsches Elektronen-Synchrotron, Hamburg, Germany
41,
W Lange
W Lange
41Deutsches Elektronen-Synchrotron, Hamburg, Germany
41,
A Lelek
A Lelek
41Deutsches Elektronen-Synchrotron, Hamburg, Germany
41,
T Lenz
T Lenz
41Deutsches Elektronen-Synchrotron, Hamburg, Germany
41,
K Lipka
K Lipka
41Deutsches Elektronen-Synchrotron, Hamburg, Germany
41,
W Lohmann
W Lohmann
41Deutsches Elektronen-Synchrotron, Hamburg, Germany
41,
R Mankel
R Mankel
41Deutsches Elektronen-Synchrotron, Hamburg, Germany
41,
I-A Melzer-Pellmann
I-A Melzer-Pellmann
41Deutsches Elektronen-Synchrotron, Hamburg, Germany
41,
A B Meyer
A B Meyer
41Deutsches Elektronen-Synchrotron, Hamburg, Germany
41,
M Meyer
M Meyer
41Deutsches Elektronen-Synchrotron, Hamburg, Germany
41,
M Missiroli
M Missiroli
41Deutsches Elektronen-Synchrotron, Hamburg, Germany
41,
G Mittag
G Mittag
41Deutsches Elektronen-Synchrotron, Hamburg, Germany
41,
J Mnich
J Mnich
41Deutsches Elektronen-Synchrotron, Hamburg, Germany
41,
V Myronenko
V Myronenko
41Deutsches Elektronen-Synchrotron, Hamburg, Germany
41,
S K Pflitsch
S K Pflitsch
41Deutsches Elektronen-Synchrotron, Hamburg, Germany
41,
D Pitzl
D Pitzl
41Deutsches Elektronen-Synchrotron, Hamburg, Germany
41,
A Raspereza
A Raspereza
41Deutsches Elektronen-Synchrotron, Hamburg, Germany
41,
M Savitskyi
M Savitskyi
41Deutsches Elektronen-Synchrotron, Hamburg, Germany
41,
P Saxena
P Saxena
41Deutsches Elektronen-Synchrotron, Hamburg, Germany
41,
P Schütze
P Schütze
41Deutsches Elektronen-Synchrotron, Hamburg, Germany
41,
C Schwanenberger
C Schwanenberger
41Deutsches Elektronen-Synchrotron, Hamburg, Germany
41,
R Shevchenko
R Shevchenko
41Deutsches Elektronen-Synchrotron, Hamburg, Germany
41,
A Singh
A Singh
41Deutsches Elektronen-Synchrotron, Hamburg, Germany
41,
N Stefaniuk
N Stefaniuk
41Deutsches Elektronen-Synchrotron, Hamburg, Germany
41,
H Tholen
H Tholen
41Deutsches Elektronen-Synchrotron, Hamburg, Germany
41,
A Vagnerini
A Vagnerini
41Deutsches Elektronen-Synchrotron, Hamburg, Germany
41,
G P Van Onsem
G P Van Onsem
41Deutsches Elektronen-Synchrotron, Hamburg, Germany
41,
R Walsh
R Walsh
41Deutsches Elektronen-Synchrotron, Hamburg, Germany
41,
Y Wen
Y Wen
41Deutsches Elektronen-Synchrotron, Hamburg, Germany
41,
K Wichmann
K Wichmann
41Deutsches Elektronen-Synchrotron, Hamburg, Germany
41,
C Wissing
C Wissing
41Deutsches Elektronen-Synchrotron, Hamburg, Germany
41,
O Zenaiev
O Zenaiev
41Deutsches Elektronen-Synchrotron, Hamburg, Germany
41,
R Aggleton
R Aggleton
42University of Hamburg, Hamburg, Germany
42,
S Bein
S Bein
42University of Hamburg, Hamburg, Germany
42,
L Benato
L Benato
42University of Hamburg, Hamburg, Germany
42,
A Benecke
A Benecke
42University of Hamburg, Hamburg, Germany
42,
V Blobel
V Blobel
42University of Hamburg, Hamburg, Germany
42,
M Centis Vignali
M Centis Vignali
42University of Hamburg, Hamburg, Germany
42,
T Dreyer
T Dreyer
42University of Hamburg, Hamburg, Germany
42,
E Garutti
E Garutti
42University of Hamburg, Hamburg, Germany
42,
D Gonzalez
D Gonzalez
42University of Hamburg, Hamburg, Germany
42,
J Haller
J Haller
42University of Hamburg, Hamburg, Germany
42,
A Hinzmann
A Hinzmann
42University of Hamburg, Hamburg, Germany
42,
A Karavdina
A Karavdina
42University of Hamburg, Hamburg, Germany
42,
G Kasieczka
G Kasieczka
42University of Hamburg, Hamburg, Germany
42,
R Klanner
R Klanner
42University of Hamburg, Hamburg, Germany
42,
R Kogler
R Kogler
42University of Hamburg, Hamburg, Germany
42,
N Kovalchuk
N Kovalchuk
42University of Hamburg, Hamburg, Germany
42,
S Kurz
S Kurz
42University of Hamburg, Hamburg, Germany
42,
V Kutzner
V Kutzner
42University of Hamburg, Hamburg, Germany
42,
J Lange
J Lange
42University of Hamburg, Hamburg, Germany
42,
D Marconi
D Marconi
42University of Hamburg, Hamburg, Germany
42,
J Multhaup
J Multhaup
42University of Hamburg, Hamburg, Germany
42,
M Niedziela
M Niedziela
42University of Hamburg, Hamburg, Germany
42,
D Nowatschin
D Nowatschin
42University of Hamburg, Hamburg, Germany
42,
A Perieanu
A Perieanu
42University of Hamburg, Hamburg, Germany
42,
A Reimers
A Reimers
42University of Hamburg, Hamburg, Germany
42,
O Rieger
O Rieger
42University of Hamburg, Hamburg, Germany
42,
C Scharf
C Scharf
42University of Hamburg, Hamburg, Germany
42,
P Schleper
P Schleper
42University of Hamburg, Hamburg, Germany
42,
S Schumann
S Schumann
42University of Hamburg, Hamburg, Germany
42,
J Schwandt
J Schwandt
42University of Hamburg, Hamburg, Germany
42,
J Sonneveld
J Sonneveld
42University of Hamburg, Hamburg, Germany
42,
H Stadie
H Stadie
42University of Hamburg, Hamburg, Germany
42,
G Steinbrück
G Steinbrück
42University of Hamburg, Hamburg, Germany
42,
F M Stober
F M Stober
42University of Hamburg, Hamburg, Germany
42,
M Stöver
M Stöver
42University of Hamburg, Hamburg, Germany
42,
D Troendle
D Troendle
42University of Hamburg, Hamburg, Germany
42,
A Vanhoefer
A Vanhoefer
42University of Hamburg, Hamburg, Germany
42,
B Vormwald
B Vormwald
42University of Hamburg, Hamburg, Germany
42,
M Akbiyik
M Akbiyik
43Karlsruher Institut für Technology, Karlsruhe, Germany
43,
C Barth
C Barth
43Karlsruher Institut für Technology, Karlsruhe, Germany
43,
M Baselga
M Baselga
43Karlsruher Institut für Technology, Karlsruhe, Germany
43,
S Baur
S Baur
43Karlsruher Institut für Technology, Karlsruhe, Germany
43,
E Butz
E Butz
43Karlsruher Institut für Technology, Karlsruhe, Germany
43,
R Caspart
R Caspart
43Karlsruher Institut für Technology, Karlsruhe, Germany
43,
T Chwalek
T Chwalek
43Karlsruher Institut für Technology, Karlsruhe, Germany
43,
F Colombo
F Colombo
43Karlsruher Institut für Technology, Karlsruhe, Germany
43,
W De Boer
W De Boer
43Karlsruher Institut für Technology, Karlsruhe, Germany
43,
A Dierlamm
A Dierlamm
43Karlsruher Institut für Technology, Karlsruhe, Germany
43,
N Faltermann
N Faltermann
43Karlsruher Institut für Technology, Karlsruhe, Germany
43,
B Freund
B Freund
43Karlsruher Institut für Technology, Karlsruhe, Germany
43,
M Giffels
M Giffels
43Karlsruher Institut für Technology, Karlsruhe, Germany
43,
M A Harrendorf
M A Harrendorf
43Karlsruher Institut für Technology, Karlsruhe, Germany
43,
F Hartmann
F Hartmann
43Karlsruher Institut für Technology, Karlsruhe, Germany
43,
S M Heindl
S M Heindl
43Karlsruher Institut für Technology, Karlsruhe, Germany
43,
U Husemann
U Husemann
43Karlsruher Institut für Technology, Karlsruhe, Germany
43,
F Kassel
F Kassel
43Karlsruher Institut für Technology, Karlsruhe, Germany
43,
I Katkov
I Katkov
43Karlsruher Institut für Technology, Karlsruhe, Germany
43,
S Kudella
S Kudella
43Karlsruher Institut für Technology, Karlsruhe, Germany
43,
H Mildner
H Mildner
43Karlsruher Institut für Technology, Karlsruhe, Germany
43,
S Mitra
S Mitra
43Karlsruher Institut für Technology, Karlsruhe, Germany
43,
M U Mozer
M U Mozer
43Karlsruher Institut für Technology, Karlsruhe, Germany
43,
Th Müller
Th Müller
43Karlsruher Institut für Technology, Karlsruhe, Germany
43,
M Plagge
M Plagge
43Karlsruher Institut für Technology, Karlsruhe, Germany
43,
G Quast
G Quast
43Karlsruher Institut für Technology, Karlsruhe, Germany
43,
K Rabbertz
K Rabbertz
43Karlsruher Institut für Technology, Karlsruhe, Germany
43,
M Schröder
M Schröder
43Karlsruher Institut für Technology, Karlsruhe, Germany
43,
I Shvetsov
I Shvetsov
43Karlsruher Institut für Technology, Karlsruhe, Germany
43,
G Sieber
G Sieber
43Karlsruher Institut für Technology, Karlsruhe, Germany
43,
H J Simonis
H J Simonis
43Karlsruher Institut für Technology, Karlsruhe, Germany
43,
R Ulrich
R Ulrich
43Karlsruher Institut für Technology, Karlsruhe, Germany
43,
S Wayand
S Wayand
43Karlsruher Institut für Technology, Karlsruhe, Germany
43,
M Weber
M Weber
43Karlsruher Institut für Technology, Karlsruhe, Germany
43,
T Weiler
T Weiler
43Karlsruher Institut für Technology, Karlsruhe, Germany
43,
S Williamson
S Williamson
43Karlsruher Institut für Technology, Karlsruhe, Germany
43,
C Wöhrmann
C Wöhrmann
43Karlsruher Institut für Technology, Karlsruhe, Germany
43,
R Wolf
R Wolf
43Karlsruher Institut für Technology, Karlsruhe, Germany
43,
G Anagnostou
G Anagnostou
44Institute of Nuclear and Particle Physics (INPP), NCSR Demokritos, Aghia Paraskevi, Greece
44,
G Daskalakis
G Daskalakis
44Institute of Nuclear and Particle Physics (INPP), NCSR Demokritos, Aghia Paraskevi, Greece
44,
T Geralis
T Geralis
44Institute of Nuclear and Particle Physics (INPP), NCSR Demokritos, Aghia Paraskevi, Greece
44,
A Kyriakis
A Kyriakis
44Institute of Nuclear and Particle Physics (INPP), NCSR Demokritos, Aghia Paraskevi, Greece
44,
D Loukas
D Loukas
44Institute of Nuclear and Particle Physics (INPP), NCSR Demokritos, Aghia Paraskevi, Greece
44,
G Paspalaki
G Paspalaki
44Institute of Nuclear and Particle Physics (INPP), NCSR Demokritos, Aghia Paraskevi, Greece
44,
I Topsis-Giotis
I Topsis-Giotis
44Institute of Nuclear and Particle Physics (INPP), NCSR Demokritos, Aghia Paraskevi, Greece
44,
G Karathanasis
G Karathanasis
45National and Kapodistrian University of Athens, Athens, Greece
45,
S Kesisoglou
S Kesisoglou
45National and Kapodistrian University of Athens, Athens, Greece
45,
P Kontaxakis
P Kontaxakis
45National and Kapodistrian University of Athens, Athens, Greece
45,
A Panagiotou
A Panagiotou
45National and Kapodistrian University of Athens, Athens, Greece
45,
N Saoulidou
N Saoulidou
45National and Kapodistrian University of Athens, Athens, Greece
45,
E Tziaferi
E Tziaferi
45National and Kapodistrian University of Athens, Athens, Greece
45,
K Vellidis
K Vellidis
45National and Kapodistrian University of Athens, Athens, Greece
45,
K Kousouris
K Kousouris
46National Technical University of Athens, Athens, Greece
46,
I Papakrivopoulos
I Papakrivopoulos
46National Technical University of Athens, Athens, Greece
46,
G Tsipolitis
G Tsipolitis
46National Technical University of Athens, Athens, Greece
46,
I Evangelou
I Evangelou
47University of Ioánnina, Ioánnina, Greece
47,
C Foudas
C Foudas
47University of Ioánnina, Ioánnina, Greece
47,
P Gianneios
P Gianneios
47University of Ioánnina, Ioánnina, Greece
47,
P Katsoulis
P Katsoulis
47University of Ioánnina, Ioánnina, Greece
47,
P Kokkas
P Kokkas
47University of Ioánnina, Ioánnina, Greece
47,
S Mallios
S Mallios
47University of Ioánnina, Ioánnina, Greece
47,
N Manthos
N Manthos
47University of Ioánnina, Ioánnina, Greece
47,
I Papadopoulos
I Papadopoulos
47University of Ioánnina, Ioánnina, Greece
47,
E Paradas
E Paradas
47University of Ioánnina, Ioánnina, Greece
47,
J Strologas
J Strologas
47University of Ioánnina, Ioánnina, Greece
47,
F A Triantis
F A Triantis
47University of Ioánnina, Ioánnina, Greece
47,
D Tsitsonis
D Tsitsonis
47University of Ioánnina, Ioánnina, Greece
47,
M Bartók
M Bartók
48MTA-ELTE Lendület CMS Particle and Nuclear Physics Group, Eötvös Loránd University, Budapest, Hungary
48,
M Csanad
M Csanad
48MTA-ELTE Lendület CMS Particle and Nuclear Physics Group, Eötvös Loránd University, Budapest, Hungary
48,
N Filipovic
N Filipovic
48MTA-ELTE Lendület CMS Particle and Nuclear Physics Group, Eötvös Loránd University, Budapest, Hungary
48,
P Major
P Major
48MTA-ELTE Lendület CMS Particle and Nuclear Physics Group, Eötvös Loránd University, Budapest, Hungary
48,
M I Nagy
M I Nagy
48MTA-ELTE Lendület CMS Particle and Nuclear Physics Group, Eötvös Loránd University, Budapest, Hungary
48,
G Pasztor
G Pasztor
48MTA-ELTE Lendület CMS Particle and Nuclear Physics Group, Eötvös Loránd University, Budapest, Hungary
48,
O Surányi
O Surányi
48MTA-ELTE Lendület CMS Particle and Nuclear Physics Group, Eötvös Loránd University, Budapest, Hungary
48,
G I Veres
G I Veres
48MTA-ELTE Lendület CMS Particle and Nuclear Physics Group, Eötvös Loránd University, Budapest, Hungary
48,
G Bencze
G Bencze
49Wigner Research Centre for Physics, Budapest, Hungary
49,
C Hajdu
C Hajdu
49Wigner Research Centre for Physics, Budapest, Hungary
49,
D Horvath
D Horvath
49Wigner Research Centre for Physics, Budapest, Hungary
49,
Á Hunyadi
Á Hunyadi
49Wigner Research Centre for Physics, Budapest, Hungary
49,
F Sikler
F Sikler
49Wigner Research Centre for Physics, Budapest, Hungary
49,
T Á Vámi
T Á Vámi
49Wigner Research Centre for Physics, Budapest, Hungary
49,
V Veszpremi
V Veszpremi
49Wigner Research Centre for Physics, Budapest, Hungary
49,
G Vesztergombi
G Vesztergombi
49Wigner Research Centre for Physics, Budapest, Hungary
49,
N Beni
N Beni
50Institute of Nuclear Research ATOMKI, Debrecen, Hungary
50,
S Czellar
S Czellar
50Institute of Nuclear Research ATOMKI, Debrecen, Hungary
50,
J Karancsi
J Karancsi
50Institute of Nuclear Research ATOMKI, Debrecen, Hungary
50,
A Makovec
A Makovec
50Institute of Nuclear Research ATOMKI, Debrecen, Hungary
50,
J Molnar
J Molnar
50Institute of Nuclear Research ATOMKI, Debrecen, Hungary
50,
Z Szillasi
Z Szillasi
50Institute of Nuclear Research ATOMKI, Debrecen, Hungary
50,
P Raics
P Raics
51Institute of Physics, University of Debrecen, Debrecen, Hungary
51,
Z L Trocsanyi
Z L Trocsanyi
51Institute of Physics, University of Debrecen, Debrecen, Hungary
51,
B Ujvari
B Ujvari
51Institute of Physics, University of Debrecen, Debrecen, Hungary
51,
S Choudhury
S Choudhury
52Indian Institute of Science (IISc), Bangalore, India
52,
J R Komaragiri
J R Komaragiri
52Indian Institute of Science (IISc), Bangalore, India
52,
P C Tiwari
P C Tiwari
52Indian Institute of Science (IISc), Bangalore, India
52,
S Bahinipati
S Bahinipati
53National Institute of Science Education and Research, HBNI, Bhubaneswar, India
53,
C Kar
C Kar
53National Institute of Science Education and Research, HBNI, Bhubaneswar, India
53,
P Mal
P Mal
53National Institute of Science Education and Research, HBNI, Bhubaneswar, India
53,
K Mandal
K Mandal
53National Institute of Science Education and Research, HBNI, Bhubaneswar, India
53,
A Nayak
A Nayak
53National Institute of Science Education and Research, HBNI, Bhubaneswar, India
53,
D K Sahoo
D K Sahoo
53National Institute of Science Education and Research, HBNI, Bhubaneswar, India
53,
S K Swain
S K Swain
53National Institute of Science Education and Research, HBNI, Bhubaneswar, India
53,
S Bansal
S Bansal
54Panjab University, Chandigarh, India
54,
S B Beri
S B Beri
54Panjab University, Chandigarh, India
54,
V Bhatnagar
V Bhatnagar
54Panjab University, Chandigarh, India
54,
S Chauhan
S Chauhan
54Panjab University, Chandigarh, India
54,
R Chawla
R Chawla
54Panjab University, Chandigarh, India
54,
N Dhingra
N Dhingra
54Panjab University, Chandigarh, India
54,
R Gupta
R Gupta
54Panjab University, Chandigarh, India
54,
A Kaur
A Kaur
54Panjab University, Chandigarh, India
54,
A Kaur
A Kaur
54Panjab University, Chandigarh, India
54,
M Kaur
M Kaur
54Panjab University, Chandigarh, India
54,
S Kaur
S Kaur
54Panjab University, Chandigarh, India
54,
R Kumar
R Kumar
54Panjab University, Chandigarh, India
54,
P Kumari
P Kumari
54Panjab University, Chandigarh, India
54,
M Lohan
M Lohan
54Panjab University, Chandigarh, India
54,
A Mehta
A Mehta
54Panjab University, Chandigarh, India
54,
K Sandeep
K Sandeep
54Panjab University, Chandigarh, India
54,
S Sharma
S Sharma
54Panjab University, Chandigarh, India
54,
J B Singh
J B Singh
54Panjab University, Chandigarh, India
54,
G Walia
G Walia
54Panjab University, Chandigarh, India
54,
A Bhardwaj
A Bhardwaj
55University of Delhi, Delhi, India
55,
B C Choudhary
B C Choudhary
55University of Delhi, Delhi, India
55,
R B Garg
R B Garg
55University of Delhi, Delhi, India
55,
M Gola
M Gola
55University of Delhi, Delhi, India
55,
S Keshri
S Keshri
55University of Delhi, Delhi, India
55,
Ashok Kumar
Ashok Kumar
55University of Delhi, Delhi, India
55,
S Malhotra
S Malhotra
55University of Delhi, Delhi, India
55,
M Naimuddin
M Naimuddin
55University of Delhi, Delhi, India
55,
P Priyanka
P Priyanka
55University of Delhi, Delhi, India
55,
K Ranjan
K Ranjan
55University of Delhi, Delhi, India
55,
Aashaq Shah
Aashaq Shah
55University of Delhi, Delhi, India
55,
R Sharma
R Sharma
55University of Delhi, Delhi, India
55,
R Bhardwaj
R Bhardwaj
56Saha Institute of Nuclear Physics, HBNI, Kolkata, India
56,
M Bharti
M Bharti
56Saha Institute of Nuclear Physics, HBNI, Kolkata, India
56,
R Bhattacharya
R Bhattacharya
56Saha Institute of Nuclear Physics, HBNI, Kolkata, India
56,
S Bhattacharya
S Bhattacharya
56Saha Institute of Nuclear Physics, HBNI, Kolkata, India
56,
U Bhawandeep
U Bhawandeep
56Saha Institute of Nuclear Physics, HBNI, Kolkata, India
56,
D Bhowmik
D Bhowmik
56Saha Institute of Nuclear Physics, HBNI, Kolkata, India
56,
S Dey
S Dey
56Saha Institute of Nuclear Physics, HBNI, Kolkata, India
56,
S Dutt
S Dutt
56Saha Institute of Nuclear Physics, HBNI, Kolkata, India
56,
S Dutta
S Dutta
56Saha Institute of Nuclear Physics, HBNI, Kolkata, India
56,
S Ghosh
S Ghosh
56Saha Institute of Nuclear Physics, HBNI, Kolkata, India
56,
K Mondal
K Mondal
56Saha Institute of Nuclear Physics, HBNI, Kolkata, India
56,
S Nandan
S Nandan
56Saha Institute of Nuclear Physics, HBNI, Kolkata, India
56,
A Purohit
A Purohit
56Saha Institute of Nuclear Physics, HBNI, Kolkata, India
56,
P K Rout
P K Rout
56Saha Institute of Nuclear Physics, HBNI, Kolkata, India
56,
A Roy
A Roy
56Saha Institute of Nuclear Physics, HBNI, Kolkata, India
56,
S Roy Chowdhury
S Roy Chowdhury
56Saha Institute of Nuclear Physics, HBNI, Kolkata, India
56,
S Sarkar
S Sarkar
56Saha Institute of Nuclear Physics, HBNI, Kolkata, India
56,
M Sharan
M Sharan
56Saha Institute of Nuclear Physics, HBNI, Kolkata, India
56,
B Singh
B Singh
56Saha Institute of Nuclear Physics, HBNI, Kolkata, India
56,
S Thakur
S Thakur
56Saha Institute of Nuclear Physics, HBNI, Kolkata, India
56,
P K Behera
P K Behera
57Indian Institute of Technology Madras, Madras, India
57,
R Chudasama
R Chudasama
58Bhabha Atomic Research Centre, Mumbai, India
58,
D Dutta
D Dutta
58Bhabha Atomic Research Centre, Mumbai, India
58,
V Jha
V Jha
58Bhabha Atomic Research Centre, Mumbai, India
58,
V Kumar
V Kumar
58Bhabha Atomic Research Centre, Mumbai, India
58,
P K Netrakanti
P K Netrakanti
58Bhabha Atomic Research Centre, Mumbai, India
58,
L M Pant
L M Pant
58Bhabha Atomic Research Centre, Mumbai, India
58,
P Shukla
P Shukla
58Bhabha Atomic Research Centre, Mumbai, India
58,
T Aziz
T Aziz
59Tata Institute of Fundamental Research-A, Mumbai, India
59,
M A Bhat
M A Bhat
59Tata Institute of Fundamental Research-A, Mumbai, India
59,
S Dugad
S Dugad
59Tata Institute of Fundamental Research-A, Mumbai, India
59,
G B Mohanty
G B Mohanty
59Tata Institute of Fundamental Research-A, Mumbai, India
59,
N Sur
N Sur
59Tata Institute of Fundamental Research-A, Mumbai, India
59,
B Sutar
B Sutar
59Tata Institute of Fundamental Research-A, Mumbai, India
59,
RavindraKumar Verma
RavindraKumar Verma
59Tata Institute of Fundamental Research-A, Mumbai, India
59,
S Banerjee
S Banerjee
60Tata Institute of Fundamental Research-B, Mumbai, India
60,
S Bhattacharya
S Bhattacharya
60Tata Institute of Fundamental Research-B, Mumbai, India
60,
S Chatterjee
S Chatterjee
60Tata Institute of Fundamental Research-B, Mumbai, India
60,
P Das
P Das
60Tata Institute of Fundamental Research-B, Mumbai, India
60,
M Guchait
M Guchait
60Tata Institute of Fundamental Research-B, Mumbai, India
60,
Sa Jain
Sa Jain
60Tata Institute of Fundamental Research-B, Mumbai, India
60,
S Kumar
S Kumar
60Tata Institute of Fundamental Research-B, Mumbai, India
60,
M Maity
M Maity
60Tata Institute of Fundamental Research-B, Mumbai, India
60,
G Majumder
G Majumder
60Tata Institute of Fundamental Research-B, Mumbai, India
60,
K Mazumdar
K Mazumdar
60Tata Institute of Fundamental Research-B, Mumbai, India
60,
N Sahoo
N Sahoo
60Tata Institute of Fundamental Research-B, Mumbai, India
60,
T Sarkar
T Sarkar
60Tata Institute of Fundamental Research-B, Mumbai, India
60,
S Chauhan
S Chauhan
61Indian Institute of Science Education and Research (IISER), Pune, India
61,
S Dube
S Dube
61Indian Institute of Science Education and Research (IISER), Pune, India
61,
V Hegde
V Hegde
61Indian Institute of Science Education and Research (IISER), Pune, India
61,
A Kapoor
A Kapoor
61Indian Institute of Science Education and Research (IISER), Pune, India
61,
K Kothekar
K Kothekar
61Indian Institute of Science Education and Research (IISER), Pune, India
61,
S Pandey
S Pandey
61Indian Institute of Science Education and Research (IISER), Pune, India
61,
A Rane
A Rane
61Indian Institute of Science Education and Research (IISER), Pune, India
61,
S Sharma
S Sharma
61Indian Institute of Science Education and Research (IISER), Pune, India
61,
S Chenarani
S Chenarani
62Institute for Research in Fundamental Sciences (IPM), Tehran, Iran
62,
E Eskandari Tadavani
E Eskandari Tadavani
62Institute for Research in Fundamental Sciences (IPM), Tehran, Iran
62,
S M Etesami
S M Etesami
62Institute for Research in Fundamental Sciences (IPM), Tehran, Iran
62,
M Khakzad
M Khakzad
62Institute for Research in Fundamental Sciences (IPM), Tehran, Iran
62,
M Mohammadi Najafabadi
M Mohammadi Najafabadi
62Institute for Research in Fundamental Sciences (IPM), Tehran, Iran
62,
M Naseri
M Naseri
62Institute for Research in Fundamental Sciences (IPM), Tehran, Iran
62,
F Rezaei Hosseinabadi
F Rezaei Hosseinabadi
62Institute for Research in Fundamental Sciences (IPM), Tehran, Iran
62,
B Safarzadeh
B Safarzadeh
62Institute for Research in Fundamental Sciences (IPM), Tehran, Iran
62,
M Zeinali
M Zeinali
62Institute for Research in Fundamental Sciences (IPM), Tehran, Iran
62,
M Felcini
M Felcini
63University College Dublin, Dublin, Ireland
63,
M Grunewald
M Grunewald
63University College Dublin, Dublin, Ireland
63,
M Abbrescia
M Abbrescia
64INFN Sezione di Bari, Università di Bari, Politecnico di Bari, Bari, Italy
64,
C Calabria
C Calabria
64INFN Sezione di Bari, Università di Bari, Politecnico di Bari, Bari, Italy
64,
A Colaleo
A Colaleo
64INFN Sezione di Bari, Università di Bari, Politecnico di Bari, Bari, Italy
64,
D Creanza
D Creanza
64INFN Sezione di Bari, Università di Bari, Politecnico di Bari, Bari, Italy
64,
L Cristella
L Cristella
64INFN Sezione di Bari, Università di Bari, Politecnico di Bari, Bari, Italy
64,
N De Filippis
N De Filippis
64INFN Sezione di Bari, Università di Bari, Politecnico di Bari, Bari, Italy
64,
M De Palma
M De Palma
64INFN Sezione di Bari, Università di Bari, Politecnico di Bari, Bari, Italy
64,
A Di Florio
A Di Florio
64INFN Sezione di Bari, Università di Bari, Politecnico di Bari, Bari, Italy
64,
F Errico
F Errico
64INFN Sezione di Bari, Università di Bari, Politecnico di Bari, Bari, Italy
64,
L Fiore
L Fiore
64INFN Sezione di Bari, Università di Bari, Politecnico di Bari, Bari, Italy
64,
A Gelmi
A Gelmi
64INFN Sezione di Bari, Università di Bari, Politecnico di Bari, Bari, Italy
64,
G Iaselli
G Iaselli
64INFN Sezione di Bari, Università di Bari, Politecnico di Bari, Bari, Italy
64,
S Lezki
S Lezki
64INFN Sezione di Bari, Università di Bari, Politecnico di Bari, Bari, Italy
64,
G Maggi
G Maggi
64INFN Sezione di Bari, Università di Bari, Politecnico di Bari, Bari, Italy
64,
M Maggi
M Maggi
64INFN Sezione di Bari, Università di Bari, Politecnico di Bari, Bari, Italy
64,
G Miniello
G Miniello
64INFN Sezione di Bari, Università di Bari, Politecnico di Bari, Bari, Italy
64,
S My
S My
64INFN Sezione di Bari, Università di Bari, Politecnico di Bari, Bari, Italy
64,
S Nuzzo
S Nuzzo
64INFN Sezione di Bari, Università di Bari, Politecnico di Bari, Bari, Italy
64,
A Pompili
A Pompili
64INFN Sezione di Bari, Università di Bari, Politecnico di Bari, Bari, Italy
64,
G Pugliese
G Pugliese
64INFN Sezione di Bari, Università di Bari, Politecnico di Bari, Bari, Italy
64,
R Radogna
R Radogna
64INFN Sezione di Bari, Università di Bari, Politecnico di Bari, Bari, Italy
64,
A Ranieri
A Ranieri
64INFN Sezione di Bari, Università di Bari, Politecnico di Bari, Bari, Italy
64,
A Sharma
A Sharma
64INFN Sezione di Bari, Università di Bari, Politecnico di Bari, Bari, Italy
64,
L Silvestris
L Silvestris
64INFN Sezione di Bari, Università di Bari, Politecnico di Bari, Bari, Italy
64,
R Venditti
R Venditti
64INFN Sezione di Bari, Università di Bari, Politecnico di Bari, Bari, Italy
64,
P Verwilligen
P Verwilligen
64INFN Sezione di Bari, Università di Bari, Politecnico di Bari, Bari, Italy
64,
G Zito
G Zito
64INFN Sezione di Bari, Università di Bari, Politecnico di Bari, Bari, Italy
64,
G Abbiendi
G Abbiendi
65INFN Sezione di Bologna, Università di Bologna, Bologna, Italy
65,
C Battilana
C Battilana
65INFN Sezione di Bologna, Università di Bologna, Bologna, Italy
65,
D Bonacorsi
D Bonacorsi
65INFN Sezione di Bologna, Università di Bologna, Bologna, Italy
65,
L Borgonovi
L Borgonovi
65INFN Sezione di Bologna, Università di Bologna, Bologna, Italy
65,
S Braibant-Giacomelli
S Braibant-Giacomelli
65INFN Sezione di Bologna, Università di Bologna, Bologna, Italy
65,
R Campanini
R Campanini
65INFN Sezione di Bologna, Università di Bologna, Bologna, Italy
65,
P Capiluppi
P Capiluppi
65INFN Sezione di Bologna, Università di Bologna, Bologna, Italy
65,
A Castro
A Castro
65INFN Sezione di Bologna, Università di Bologna, Bologna, Italy
65,
F R Cavallo
F R Cavallo
65INFN Sezione di Bologna, Università di Bologna, Bologna, Italy
65,
S S Chhibra
S S Chhibra
65INFN Sezione di Bologna, Università di Bologna, Bologna, Italy
65,
C Ciocca
C Ciocca
65INFN Sezione di Bologna, Università di Bologna, Bologna, Italy
65,
G Codispoti
G Codispoti
65INFN Sezione di Bologna, Università di Bologna, Bologna, Italy
65,
M Cuffiani
M Cuffiani
65INFN Sezione di Bologna, Università di Bologna, Bologna, Italy
65,
G M Dallavalle
G M Dallavalle
65INFN Sezione di Bologna, Università di Bologna, Bologna, Italy
65,
F Fabbri
F Fabbri
65INFN Sezione di Bologna, Università di Bologna, Bologna, Italy
65,
A Fanfani
A Fanfani
65INFN Sezione di Bologna, Università di Bologna, Bologna, Italy
65,
P Giacomelli
P Giacomelli
65INFN Sezione di Bologna, Università di Bologna, Bologna, Italy
65,
C Grandi
C Grandi
65INFN Sezione di Bologna, Università di Bologna, Bologna, Italy
65,
L Guiducci
L Guiducci
65INFN Sezione di Bologna, Università di Bologna, Bologna, Italy
65,
F Iemmi
F Iemmi
65INFN Sezione di Bologna, Università di Bologna, Bologna, Italy
65,
S Marcellini
S Marcellini
65INFN Sezione di Bologna, Università di Bologna, Bologna, Italy
65,
G Masetti
G Masetti
65INFN Sezione di Bologna, Università di Bologna, Bologna, Italy
65,
A Montanari
A Montanari
65INFN Sezione di Bologna, Università di Bologna, Bologna, Italy
65,
F L Navarria
F L Navarria
65INFN Sezione di Bologna, Università di Bologna, Bologna, Italy
65,
A Perrotta
A Perrotta
65INFN Sezione di Bologna, Università di Bologna, Bologna, Italy
65,
F Primavera
F Primavera
65INFN Sezione di Bologna, Università di Bologna, Bologna, Italy
65,
A M Rossi
A M Rossi
65INFN Sezione di Bologna, Università di Bologna, Bologna, Italy
65,
T Rovelli
T Rovelli
65INFN Sezione di Bologna, Università di Bologna, Bologna, Italy
65,
G P Siroli
G P Siroli
65INFN Sezione di Bologna, Università di Bologna, Bologna, Italy
65,
N Tosi
N Tosi
65INFN Sezione di Bologna, Università di Bologna, Bologna, Italy
65,
S Albergo
S Albergo
66INFN Sezione di Catania, Università di Catania, Catania, Italy
66,
A Di Mattia
A Di Mattia
66INFN Sezione di Catania, Università di Catania, Catania, Italy
66,
R Potenza
R Potenza
66INFN Sezione di Catania, Università di Catania, Catania, Italy
66,
A Tricomi
A Tricomi
66INFN Sezione di Catania, Università di Catania, Catania, Italy
66,
C Tuve
C Tuve
66INFN Sezione di Catania, Università di Catania, Catania, Italy
66,
G Barbagli
G Barbagli
67INFN Sezione di Firenze, Università di Firenze, Florence, Italy
67,
K Chatterjee
K Chatterjee
67INFN Sezione di Firenze, Università di Firenze, Florence, Italy
67,
V Ciulli
V Ciulli
67INFN Sezione di Firenze, Università di Firenze, Florence, Italy
67,
C Civinini
C Civinini
67INFN Sezione di Firenze, Università di Firenze, Florence, Italy
67,
R D’Alessandro
R D’Alessandro
67INFN Sezione di Firenze, Università di Firenze, Florence, Italy
67,
E Focardi
E Focardi
67INFN Sezione di Firenze, Università di Firenze, Florence, Italy
67,
G Latino
G Latino
67INFN Sezione di Firenze, Università di Firenze, Florence, Italy
67,
P Lenzi
P Lenzi
67INFN Sezione di Firenze, Università di Firenze, Florence, Italy
67,
M Meschini
M Meschini
67INFN Sezione di Firenze, Università di Firenze, Florence, Italy
67,
S Paoletti
S Paoletti
67INFN Sezione di Firenze, Università di Firenze, Florence, Italy
67,
L Russo
L Russo
67INFN Sezione di Firenze, Università di Firenze, Florence, Italy
67,
G Sguazzoni
G Sguazzoni
67INFN Sezione di Firenze, Università di Firenze, Florence, Italy
67,
D Strom
D Strom
67INFN Sezione di Firenze, Università di Firenze, Florence, Italy
67,
L Viliani
L Viliani
67INFN Sezione di Firenze, Università di Firenze, Florence, Italy
67,
L Benussi
L Benussi
68INFN Laboratori Nazionali di Frascati, Frascati, Italy
68,
S Bianco
S Bianco
68INFN Laboratori Nazionali di Frascati, Frascati, Italy
68,
F Fabbri
F Fabbri
68INFN Laboratori Nazionali di Frascati, Frascati, Italy
68,
D Piccolo
D Piccolo
68INFN Laboratori Nazionali di Frascati, Frascati, Italy
68,
F Ferro
F Ferro
69INFN Sezione di Genova, Università di Genova, Genoa, Italy
69,
F Ravera
F Ravera
69INFN Sezione di Genova, Università di Genova, Genoa, Italy
69,
E Robutti
E Robutti
69INFN Sezione di Genova, Università di Genova, Genoa, Italy
69,
S Tosi
S Tosi
69INFN Sezione di Genova, Università di Genova, Genoa, Italy
69,
A Benaglia
A Benaglia
70INFN Sezione di Milano-Bicocca, Università di Milano-Bicocca, Milan, Italy
70,
A Beschi
A Beschi
70INFN Sezione di Milano-Bicocca, Università di Milano-Bicocca, Milan, Italy
70,
L Brianza
L Brianza
70INFN Sezione di Milano-Bicocca, Università di Milano-Bicocca, Milan, Italy
70,
F Brivio
F Brivio
70INFN Sezione di Milano-Bicocca, Università di Milano-Bicocca, Milan, Italy
70,
V Ciriolo
V Ciriolo
70INFN Sezione di Milano-Bicocca, Università di Milano-Bicocca, Milan, Italy
70,
S Di Guida
S Di Guida
70INFN Sezione di Milano-Bicocca, Università di Milano-Bicocca, Milan, Italy
70,
M E Dinardo
M E Dinardo
70INFN Sezione di Milano-Bicocca, Università di Milano-Bicocca, Milan, Italy
70,
S Fiorendi
S Fiorendi
70INFN Sezione di Milano-Bicocca, Università di Milano-Bicocca, Milan, Italy
70,
S Gennai
S Gennai
70INFN Sezione di Milano-Bicocca, Università di Milano-Bicocca, Milan, Italy
70,
A Ghezzi
A Ghezzi
70INFN Sezione di Milano-Bicocca, Università di Milano-Bicocca, Milan, Italy
70,
P Govoni
P Govoni
70INFN Sezione di Milano-Bicocca, Università di Milano-Bicocca, Milan, Italy
70,
M Malberti
M Malberti
70INFN Sezione di Milano-Bicocca, Università di Milano-Bicocca, Milan, Italy
70,
S Malvezzi
S Malvezzi
70INFN Sezione di Milano-Bicocca, Università di Milano-Bicocca, Milan, Italy
70,
A Massironi
A Massironi
70INFN Sezione di Milano-Bicocca, Università di Milano-Bicocca, Milan, Italy
70,
D Menasce
D Menasce
70INFN Sezione di Milano-Bicocca, Università di Milano-Bicocca, Milan, Italy
70,
L Moroni
L Moroni
70INFN Sezione di Milano-Bicocca, Università di Milano-Bicocca, Milan, Italy
70,
M Paganoni
M Paganoni
70INFN Sezione di Milano-Bicocca, Università di Milano-Bicocca, Milan, Italy
70,
D Pedrini
D Pedrini
70INFN Sezione di Milano-Bicocca, Università di Milano-Bicocca, Milan, Italy
70,
S Ragazzi
S Ragazzi
70INFN Sezione di Milano-Bicocca, Università di Milano-Bicocca, Milan, Italy
70,
T Tabarelli de Fatis
T Tabarelli de Fatis
70INFN Sezione di Milano-Bicocca, Università di Milano-Bicocca, Milan, Italy
70,
S Buontempo
S Buontempo
71INFN Sezione di Napoli, Università di Napoli ‘Federico II’, Naples, Italy, Università della Basilicata, Potenza, Italy, Università G. Marconi, Rome, Italy
71,
N Cavallo
N Cavallo
71INFN Sezione di Napoli, Università di Napoli ‘Federico II’, Naples, Italy, Università della Basilicata, Potenza, Italy, Università G. Marconi, Rome, Italy
71,
A Di Crescenzo
A Di Crescenzo
71INFN Sezione di Napoli, Università di Napoli ‘Federico II’, Naples, Italy, Università della Basilicata, Potenza, Italy, Università G. Marconi, Rome, Italy
71,
F Fabozzi
F Fabozzi
71INFN Sezione di Napoli, Università di Napoli ‘Federico II’, Naples, Italy, Università della Basilicata, Potenza, Italy, Università G. Marconi, Rome, Italy
71,
F Fienga
F Fienga
71INFN Sezione di Napoli, Università di Napoli ‘Federico II’, Naples, Italy, Università della Basilicata, Potenza, Italy, Università G. Marconi, Rome, Italy
71,
G Galati
G Galati
71INFN Sezione di Napoli, Università di Napoli ‘Federico II’, Naples, Italy, Università della Basilicata, Potenza, Italy, Università G. Marconi, Rome, Italy
71,
A O M Iorio
A O M Iorio
71INFN Sezione di Napoli, Università di Napoli ‘Federico II’, Naples, Italy, Università della Basilicata, Potenza, Italy, Università G. Marconi, Rome, Italy
71,
W A Khan
W A Khan
71INFN Sezione di Napoli, Università di Napoli ‘Federico II’, Naples, Italy, Università della Basilicata, Potenza, Italy, Università G. Marconi, Rome, Italy
71,
L Lista
L Lista
71INFN Sezione di Napoli, Università di Napoli ‘Federico II’, Naples, Italy, Università della Basilicata, Potenza, Italy, Università G. Marconi, Rome, Italy
71,
S Meola
S Meola
71INFN Sezione di Napoli, Università di Napoli ‘Federico II’, Naples, Italy, Università della Basilicata, Potenza, Italy, Università G. Marconi, Rome, Italy
71,
P Paolucci
P Paolucci
71INFN Sezione di Napoli, Università di Napoli ‘Federico II’, Naples, Italy, Università della Basilicata, Potenza, Italy, Università G. Marconi, Rome, Italy
71,
C Sciacca
C Sciacca
71INFN Sezione di Napoli, Università di Napoli ‘Federico II’, Naples, Italy, Università della Basilicata, Potenza, Italy, Università G. Marconi, Rome, Italy
71,
E Voevodina
E Voevodina
71INFN Sezione di Napoli, Università di Napoli ‘Federico II’, Naples, Italy, Università della Basilicata, Potenza, Italy, Università G. Marconi, Rome, Italy
71,
P Azzi
P Azzi
72INFN Sezione di Padova, Università di Padova, Padua, Italy, Università di Trento, Trento, Italy
72,
N Bacchetta
N Bacchetta
72INFN Sezione di Padova, Università di Padova, Padua, Italy, Università di Trento, Trento, Italy
72,
D Bisello
D Bisello
72INFN Sezione di Padova, Università di Padova, Padua, Italy, Università di Trento, Trento, Italy
72,
A Boletti
A Boletti
72INFN Sezione di Padova, Università di Padova, Padua, Italy, Università di Trento, Trento, Italy
72,
A Bragagnolo
A Bragagnolo
72INFN Sezione di Padova, Università di Padova, Padua, Italy, Università di Trento, Trento, Italy
72,
R Carlin
R Carlin
72INFN Sezione di Padova, Università di Padova, Padua, Italy, Università di Trento, Trento, Italy
72,
P Checchia
P Checchia
72INFN Sezione di Padova, Università di Padova, Padua, Italy, Università di Trento, Trento, Italy
72,
M Dall’Osso
M Dall’Osso
72INFN Sezione di Padova, Università di Padova, Padua, Italy, Università di Trento, Trento, Italy
72,
P De Castro Manzano
P De Castro Manzano
72INFN Sezione di Padova, Università di Padova, Padua, Italy, Università di Trento, Trento, Italy
72,
T Dorigo
T Dorigo
72INFN Sezione di Padova, Università di Padova, Padua, Italy, Università di Trento, Trento, Italy
72,
F Gasparini
F Gasparini
72INFN Sezione di Padova, Università di Padova, Padua, Italy, Università di Trento, Trento, Italy
72,
A Gozzelino
A Gozzelino
72INFN Sezione di Padova, Università di Padova, Padua, Italy, Università di Trento, Trento, Italy
72,
S Lacaprara
S Lacaprara
72INFN Sezione di Padova, Università di Padova, Padua, Italy, Università di Trento, Trento, Italy
72,
P Lujan
P Lujan
72INFN Sezione di Padova, Università di Padova, Padua, Italy, Università di Trento, Trento, Italy
72,
M Margoni
M Margoni
72INFN Sezione di Padova, Università di Padova, Padua, Italy, Università di Trento, Trento, Italy
72,
A T Meneguzzo
A T Meneguzzo
72INFN Sezione di Padova, Università di Padova, Padua, Italy, Università di Trento, Trento, Italy
72,
N Pozzobon
N Pozzobon
72INFN Sezione di Padova, Università di Padova, Padua, Italy, Università di Trento, Trento, Italy
72,
P Ronchese
P Ronchese
72INFN Sezione di Padova, Università di Padova, Padua, Italy, Università di Trento, Trento, Italy
72,
R Rossin
R Rossin
72INFN Sezione di Padova, Università di Padova, Padua, Italy, Università di Trento, Trento, Italy
72,
F Simonetto
F Simonetto
72INFN Sezione di Padova, Università di Padova, Padua, Italy, Università di Trento, Trento, Italy
72,
A Tiko
A Tiko
72INFN Sezione di Padova, Università di Padova, Padua, Italy, Università di Trento, Trento, Italy
72,
E Torassa
E Torassa
72INFN Sezione di Padova, Università di Padova, Padua, Italy, Università di Trento, Trento, Italy
72,
S Ventura
S Ventura
72INFN Sezione di Padova, Università di Padova, Padua, Italy, Università di Trento, Trento, Italy
72,
M Zanetti
M Zanetti
72INFN Sezione di Padova, Università di Padova, Padua, Italy, Università di Trento, Trento, Italy
72,
P Zotto
P Zotto
72INFN Sezione di Padova, Università di Padova, Padua, Italy, Università di Trento, Trento, Italy
72,
G Zumerle
G Zumerle
72INFN Sezione di Padova, Università di Padova, Padua, Italy, Università di Trento, Trento, Italy
72,
A Braghieri
A Braghieri
73INFN Sezione di Pavia, Università di Pavia, Pavia, Italy
73,
A Magnani
A Magnani
73INFN Sezione di Pavia, Università di Pavia, Pavia, Italy
73,
P Montagna
P Montagna
73INFN Sezione di Pavia, Università di Pavia, Pavia, Italy
73,
S P Ratti
S P Ratti
73INFN Sezione di Pavia, Università di Pavia, Pavia, Italy
73,
V Re
V Re
73INFN Sezione di Pavia, Università di Pavia, Pavia, Italy
73,
M Ressegotti
M Ressegotti
73INFN Sezione di Pavia, Università di Pavia, Pavia, Italy
73,
C Riccardi
C Riccardi
73INFN Sezione di Pavia, Università di Pavia, Pavia, Italy
73,
P Salvini
P Salvini
73INFN Sezione di Pavia, Università di Pavia, Pavia, Italy
73,
I Vai
I Vai
73INFN Sezione di Pavia, Università di Pavia, Pavia, Italy
73,
P Vitulo
P Vitulo
73INFN Sezione di Pavia, Università di Pavia, Pavia, Italy
73,
L Alunni Solestizi
L Alunni Solestizi
74INFN Sezione di Perugia, Università di Perugia, Perugia, Italy
74,
M Biasini
M Biasini
74INFN Sezione di Perugia, Università di Perugia, Perugia, Italy
74,
G M Bilei
G M Bilei
74INFN Sezione di Perugia, Università di Perugia, Perugia, Italy
74,
C Cecchi
C Cecchi
74INFN Sezione di Perugia, Università di Perugia, Perugia, Italy
74,
D Ciangottini
D Ciangottini
74INFN Sezione di Perugia, Università di Perugia, Perugia, Italy
74,
L Fanò
L Fanò
74INFN Sezione di Perugia, Università di Perugia, Perugia, Italy
74,
P Lariccia
P Lariccia
74INFN Sezione di Perugia, Università di Perugia, Perugia, Italy
74,
E Manoni
E Manoni
74INFN Sezione di Perugia, Università di Perugia, Perugia, Italy
74,
G Mantovani
G Mantovani
74INFN Sezione di Perugia, Università di Perugia, Perugia, Italy
74,
V Mariani
V Mariani
74INFN Sezione di Perugia, Università di Perugia, Perugia, Italy
74,
M Menichelli
M Menichelli
74INFN Sezione di Perugia, Università di Perugia, Perugia, Italy
74,
A Rossi
A Rossi
74INFN Sezione di Perugia, Università di Perugia, Perugia, Italy
74,
A Santocchia
A Santocchia
74INFN Sezione di Perugia, Università di Perugia, Perugia, Italy
74,
D Spiga
D Spiga
74INFN Sezione di Perugia, Università di Perugia, Perugia, Italy
74,
K Androsov
K Androsov
75INFN Sezione di Pisa, Università di Pisa, Scuola Normale Superiore di Pisa, Pisa, Italy
75,
P Azzurri
P Azzurri
75INFN Sezione di Pisa, Università di Pisa, Scuola Normale Superiore di Pisa, Pisa, Italy
75,
G Bagliesi
G Bagliesi
75INFN Sezione di Pisa, Università di Pisa, Scuola Normale Superiore di Pisa, Pisa, Italy
75,
L Bianchini
L Bianchini
75INFN Sezione di Pisa, Università di Pisa, Scuola Normale Superiore di Pisa, Pisa, Italy
75,
T Boccali
T Boccali
75INFN Sezione di Pisa, Università di Pisa, Scuola Normale Superiore di Pisa, Pisa, Italy
75,
L Borrello
L Borrello
75INFN Sezione di Pisa, Università di Pisa, Scuola Normale Superiore di Pisa, Pisa, Italy
75,
R Castaldi
R Castaldi
75INFN Sezione di Pisa, Università di Pisa, Scuola Normale Superiore di Pisa, Pisa, Italy
75,
M A Ciocci
M A Ciocci
75INFN Sezione di Pisa, Università di Pisa, Scuola Normale Superiore di Pisa, Pisa, Italy
75,
R Dell’Orso
R Dell’Orso
75INFN Sezione di Pisa, Università di Pisa, Scuola Normale Superiore di Pisa, Pisa, Italy
75,
G Fedi
G Fedi
75INFN Sezione di Pisa, Università di Pisa, Scuola Normale Superiore di Pisa, Pisa, Italy
75,
L Giannini
L Giannini
75INFN Sezione di Pisa, Università di Pisa, Scuola Normale Superiore di Pisa, Pisa, Italy
75,
A Giassi
A Giassi
75INFN Sezione di Pisa, Università di Pisa, Scuola Normale Superiore di Pisa, Pisa, Italy
75,
M T Grippo
M T Grippo
75INFN Sezione di Pisa, Università di Pisa, Scuola Normale Superiore di Pisa, Pisa, Italy
75,
F Ligabue
F Ligabue
75INFN Sezione di Pisa, Università di Pisa, Scuola Normale Superiore di Pisa, Pisa, Italy
75,
E Manca
E Manca
75INFN Sezione di Pisa, Università di Pisa, Scuola Normale Superiore di Pisa, Pisa, Italy
75,
G Mandorli
G Mandorli
75INFN Sezione di Pisa, Università di Pisa, Scuola Normale Superiore di Pisa, Pisa, Italy
75,
A Messineo
A Messineo
75INFN Sezione di Pisa, Università di Pisa, Scuola Normale Superiore di Pisa, Pisa, Italy
75,
F Palla
F Palla
75INFN Sezione di Pisa, Università di Pisa, Scuola Normale Superiore di Pisa, Pisa, Italy
75,
A Rizzi
A Rizzi
75INFN Sezione di Pisa, Università di Pisa, Scuola Normale Superiore di Pisa, Pisa, Italy
75,
P Spagnolo
P Spagnolo
75INFN Sezione di Pisa, Università di Pisa, Scuola Normale Superiore di Pisa, Pisa, Italy
75,
R Tenchini
R Tenchini
75INFN Sezione di Pisa, Università di Pisa, Scuola Normale Superiore di Pisa, Pisa, Italy
75,
G Tonelli
G Tonelli
75INFN Sezione di Pisa, Università di Pisa, Scuola Normale Superiore di Pisa, Pisa, Italy
75,
A Venturi
A Venturi
75INFN Sezione di Pisa, Università di Pisa, Scuola Normale Superiore di Pisa, Pisa, Italy
75,
P G Verdini
P G Verdini
75INFN Sezione di Pisa, Università di Pisa, Scuola Normale Superiore di Pisa, Pisa, Italy
75,
L Barone
L Barone
76INFN Sezione di Roma, Sapienza Università di Roma, Rome, Italy
76,
F Cavallari
F Cavallari
76INFN Sezione di Roma, Sapienza Università di Roma, Rome, Italy
76,
M Cipriani
M Cipriani
76INFN Sezione di Roma, Sapienza Università di Roma, Rome, Italy
76,
N Daci
N Daci
76INFN Sezione di Roma, Sapienza Università di Roma, Rome, Italy
76,
D Del Re
D Del Re
76INFN Sezione di Roma, Sapienza Università di Roma, Rome, Italy
76,
E Di Marco
E Di Marco
76INFN Sezione di Roma, Sapienza Università di Roma, Rome, Italy
76,
M Diemoz
M Diemoz
76INFN Sezione di Roma, Sapienza Università di Roma, Rome, Italy
76,
S Gelli
S Gelli
76INFN Sezione di Roma, Sapienza Università di Roma, Rome, Italy
76,
E Longo
E Longo
76INFN Sezione di Roma, Sapienza Università di Roma, Rome, Italy
76,
B Marzocchi
B Marzocchi
76INFN Sezione di Roma, Sapienza Università di Roma, Rome, Italy
76,
P Meridiani
P Meridiani
76INFN Sezione di Roma, Sapienza Università di Roma, Rome, Italy
76,
G Organtini
G Organtini
76INFN Sezione di Roma, Sapienza Università di Roma, Rome, Italy
76,
F Pandolfi
F Pandolfi
76INFN Sezione di Roma, Sapienza Università di Roma, Rome, Italy
76,
R Paramatti
R Paramatti
76INFN Sezione di Roma, Sapienza Università di Roma, Rome, Italy
76,
F Preiato
F Preiato
76INFN Sezione di Roma, Sapienza Università di Roma, Rome, Italy
76,
S Rahatlou
S Rahatlou
76INFN Sezione di Roma, Sapienza Università di Roma, Rome, Italy
76,
C Rovelli
C Rovelli
76INFN Sezione di Roma, Sapienza Università di Roma, Rome, Italy
76,
F Santanastasio
F Santanastasio
76INFN Sezione di Roma, Sapienza Università di Roma, Rome, Italy
76,
N Amapane
N Amapane
77INFN Sezione di Torino, Università di Torino, Torino, Italy, Università del Piemonte Orientale, Novara, Italy
77,
R Arcidiacono
R Arcidiacono
77INFN Sezione di Torino, Università di Torino, Torino, Italy, Università del Piemonte Orientale, Novara, Italy
77,
S Argiro
S Argiro
77INFN Sezione di Torino, Università di Torino, Torino, Italy, Università del Piemonte Orientale, Novara, Italy
77,
M Arneodo
M Arneodo
77INFN Sezione di Torino, Università di Torino, Torino, Italy, Università del Piemonte Orientale, Novara, Italy
77,
N Bartosik
N Bartosik
77INFN Sezione di Torino, Università di Torino, Torino, Italy, Università del Piemonte Orientale, Novara, Italy
77,
R Bellan
R Bellan
77INFN Sezione di Torino, Università di Torino, Torino, Italy, Università del Piemonte Orientale, Novara, Italy
77,
C Biino
C Biino
77INFN Sezione di Torino, Università di Torino, Torino, Italy, Università del Piemonte Orientale, Novara, Italy
77,
N Cartiglia
N Cartiglia
77INFN Sezione di Torino, Università di Torino, Torino, Italy, Università del Piemonte Orientale, Novara, Italy
77,
F Cenna
F Cenna
77INFN Sezione di Torino, Università di Torino, Torino, Italy, Università del Piemonte Orientale, Novara, Italy
77,
S Cometti
S Cometti
77INFN Sezione di Torino, Università di Torino, Torino, Italy, Università del Piemonte Orientale, Novara, Italy
77,
M Costa
M Costa
77INFN Sezione di Torino, Università di Torino, Torino, Italy, Università del Piemonte Orientale, Novara, Italy
77,
R Covarelli
R Covarelli
77INFN Sezione di Torino, Università di Torino, Torino, Italy, Università del Piemonte Orientale, Novara, Italy
77,
N Demaria
N Demaria
77INFN Sezione di Torino, Università di Torino, Torino, Italy, Università del Piemonte Orientale, Novara, Italy
77,
B Kiani
B Kiani
77INFN Sezione di Torino, Università di Torino, Torino, Italy, Università del Piemonte Orientale, Novara, Italy
77,
C Mariotti
C Mariotti
77INFN Sezione di Torino, Università di Torino, Torino, Italy, Università del Piemonte Orientale, Novara, Italy
77,
S Maselli
S Maselli
77INFN Sezione di Torino, Università di Torino, Torino, Italy, Università del Piemonte Orientale, Novara, Italy
77,
E Migliore
E Migliore
77INFN Sezione di Torino, Università di Torino, Torino, Italy, Università del Piemonte Orientale, Novara, Italy
77,
V Monaco
V Monaco
77INFN Sezione di Torino, Università di Torino, Torino, Italy, Università del Piemonte Orientale, Novara, Italy
77,
E Monteil
E Monteil
77INFN Sezione di Torino, Università di Torino, Torino, Italy, Università del Piemonte Orientale, Novara, Italy
77,
M Monteno
M Monteno
77INFN Sezione di Torino, Università di Torino, Torino, Italy, Università del Piemonte Orientale, Novara, Italy
77,
M M Obertino
M M Obertino
77INFN Sezione di Torino, Università di Torino, Torino, Italy, Università del Piemonte Orientale, Novara, Italy
77,
L Pacher
L Pacher
77INFN Sezione di Torino, Università di Torino, Torino, Italy, Università del Piemonte Orientale, Novara, Italy
77,
N Pastrone
N Pastrone
77INFN Sezione di Torino, Università di Torino, Torino, Italy, Università del Piemonte Orientale, Novara, Italy
77,
M Pelliccioni
M Pelliccioni
77INFN Sezione di Torino, Università di Torino, Torino, Italy, Università del Piemonte Orientale, Novara, Italy
77,
G L Pinna Angioni
G L Pinna Angioni
77INFN Sezione di Torino, Università di Torino, Torino, Italy, Università del Piemonte Orientale, Novara, Italy
77,
A Romero
A Romero
77INFN Sezione di Torino, Università di Torino, Torino, Italy, Università del Piemonte Orientale, Novara, Italy
77,
M Ruspa
M Ruspa
77INFN Sezione di Torino, Università di Torino, Torino, Italy, Università del Piemonte Orientale, Novara, Italy
77,
R Sacchi
R Sacchi
77INFN Sezione di Torino, Università di Torino, Torino, Italy, Università del Piemonte Orientale, Novara, Italy
77,
K Shchelina
K Shchelina
77INFN Sezione di Torino, Università di Torino, Torino, Italy, Università del Piemonte Orientale, Novara, Italy
77,
V Sola
V Sola
77INFN Sezione di Torino, Università di Torino, Torino, Italy, Università del Piemonte Orientale, Novara, Italy
77,
A Solano
A Solano
77INFN Sezione di Torino, Università di Torino, Torino, Italy, Università del Piemonte Orientale, Novara, Italy
77,
D Soldi
D Soldi
77INFN Sezione di Torino, Università di Torino, Torino, Italy, Università del Piemonte Orientale, Novara, Italy
77,
A Staiano
A Staiano
77INFN Sezione di Torino, Università di Torino, Torino, Italy, Università del Piemonte Orientale, Novara, Italy
77,
S Belforte
S Belforte
78INFN Sezione di Trieste, Università di Trieste, Trieste, Italy
78,
V Candelise
V Candelise
78INFN Sezione di Trieste, Università di Trieste, Trieste, Italy
78,
M Casarsa
M Casarsa
78INFN Sezione di Trieste, Università di Trieste, Trieste, Italy
78,
F Cossutti
F Cossutti
78INFN Sezione di Trieste, Università di Trieste, Trieste, Italy
78,
G Della Ricca
G Della Ricca
78INFN Sezione di Trieste, Università di Trieste, Trieste, Italy
78,
F Vazzoler
F Vazzoler
78INFN Sezione di Trieste, Università di Trieste, Trieste, Italy
78,
A Zanetti
A Zanetti
78INFN Sezione di Trieste, Università di Trieste, Trieste, Italy
78,
D H Kim
D H Kim
79Kyungpook National University, Daegu, South Korea
79,
G N Kim
G N Kim
79Kyungpook National University, Daegu, South Korea
79,
M S Kim
M S Kim
79Kyungpook National University, Daegu, South Korea
79,
J Lee
J Lee
79Kyungpook National University, Daegu, South Korea
79,
S Lee
S Lee
79Kyungpook National University, Daegu, South Korea
79,
S W Lee
S W Lee
79Kyungpook National University, Daegu, South Korea
79,
C S Moon
C S Moon
79Kyungpook National University, Daegu, South Korea
79,
Y D Oh
Y D Oh
79Kyungpook National University, Daegu, South Korea
79,
S Sekmen
S Sekmen
79Kyungpook National University, Daegu, South Korea
79,
D C Son
D C Son
79Kyungpook National University, Daegu, South Korea
79,
Y C Yang
Y C Yang
79Kyungpook National University, Daegu, South Korea
79,
H Kim
H Kim
80Institute for Universe and Elementary Particles, Chonnam National University, Kwangju, Korea
80,
D H Moon
D H Moon
80Institute for Universe and Elementary Particles, Chonnam National University, Kwangju, Korea
80,
G Oh
G Oh
80Institute for Universe and Elementary Particles, Chonnam National University, Kwangju, Korea
80,
J Goh
J Goh
81Hanyang University, Seoul, Korea
81,
T J Kim
T J Kim
81Hanyang University, Seoul, Korea
81,
S Cho
S Cho
82Korea University, Seoul, Korea
82,
S Choi
S Choi
82Korea University, Seoul, Korea
82,
Y Go
Y Go
82Korea University, Seoul, Korea
82,
D Gyun
D Gyun
82Korea University, Seoul, Korea
82,
S Ha
S Ha
82Korea University, Seoul, Korea
82,
B Hong
B Hong
82Korea University, Seoul, Korea
82,
Y Jo
Y Jo
82Korea University, Seoul, Korea
82,
K Lee
K Lee
82Korea University, Seoul, Korea
82,
K S Lee
K S Lee
82Korea University, Seoul, Korea
82,
S Lee
S Lee
82Korea University, Seoul, Korea
82,
J Lim
J Lim
82Korea University, Seoul, Korea
82,
S K Park
S K Park
82Korea University, Seoul, Korea
82,
Y Roh
Y Roh
82Korea University, Seoul, Korea
82,
H S Kim
H S Kim
83Sejong University, Seoul, Korea
83,
J Almond
J Almond
84Seoul National University, Seoul, Korea
84,
J Kim
J Kim
84Seoul National University, Seoul, Korea
84,
J S Kim
J S Kim
84Seoul National University, Seoul, Korea
84,
H Lee
H Lee
84Seoul National University, Seoul, Korea
84,
K Lee
K Lee
84Seoul National University, Seoul, Korea
84,
K Nam
K Nam
84Seoul National University, Seoul, Korea
84,
S B Oh
S B Oh
84Seoul National University, Seoul, Korea
84,
B C Radburn-Smith
B C Radburn-Smith
84Seoul National University, Seoul, Korea
84,
S h Seo
S h Seo
84Seoul National University, Seoul, Korea
84,
U K Yang
U K Yang
84Seoul National University, Seoul, Korea
84,
H D Yoo
H D Yoo
84Seoul National University, Seoul, Korea
84,
G B Yu
G B Yu
84Seoul National University, Seoul, Korea
84,
D Jeon
D Jeon
85University of Seoul, Seoul, Korea
85,
H Kim
H Kim
85University of Seoul, Seoul, Korea
85,
J H Kim
J H Kim
85University of Seoul, Seoul, Korea
85,
J S H Lee
J S H Lee
85University of Seoul, Seoul, Korea
85,
I C Park
I C Park
85University of Seoul, Seoul, Korea
85,
Y Choi
Y Choi
86Sungkyunkwan University, Suwon, Korea
86,
C Hwang
C Hwang
86Sungkyunkwan University, Suwon, Korea
86,
J Lee
J Lee
86Sungkyunkwan University, Suwon, Korea
86,
I Yu
I Yu
86Sungkyunkwan University, Suwon, Korea
86,
V Dudenas
V Dudenas
87Vilnius University, Vilnius, Lithuania
87,
A Juodagalvis
A Juodagalvis
87Vilnius University, Vilnius, Lithuania
87,
J Vaitkus
J Vaitkus
87Vilnius University, Vilnius, Lithuania
87,
I Ahmed
I Ahmed
88National Centre for Particle Physics, Universiti Malaya, Kuala Lumpur, Malaysia
88,
Z A Ibrahim
Z A Ibrahim
88National Centre for Particle Physics, Universiti Malaya, Kuala Lumpur, Malaysia
88,
F Maulida
F Maulida
88National Centre for Particle Physics, Universiti Malaya, Kuala Lumpur, Malaysia
88,
M A B Md Ali
M A B Md Ali
88National Centre for Particle Physics, Universiti Malaya, Kuala Lumpur, Malaysia
88,
F Mohamad Idris
F Mohamad Idris
88National Centre for Particle Physics, Universiti Malaya, Kuala Lumpur, Malaysia
88,
W A T Wan Abdullah
W A T Wan Abdullah
88National Centre for Particle Physics, Universiti Malaya, Kuala Lumpur, Malaysia
88,
M N Yusli
M N Yusli
88National Centre for Particle Physics, Universiti Malaya, Kuala Lumpur, Malaysia
88,
Z Zolkapli
Z Zolkapli
88National Centre for Particle Physics, Universiti Malaya, Kuala Lumpur, Malaysia
88,
H Castilla-Valdez
H Castilla-Valdez
89Centro de Investigacion y de Estudios Avanzados del IPN, Mexico City, Mexico
89,
E De La Cruz-Burelo
E De La Cruz-Burelo
89Centro de Investigacion y de Estudios Avanzados del IPN, Mexico City, Mexico
89,
M C Duran-Osuna
M C Duran-Osuna
89Centro de Investigacion y de Estudios Avanzados del IPN, Mexico City, Mexico
89,
I Heredia-De La Cruz
I Heredia-De La Cruz
89Centro de Investigacion y de Estudios Avanzados del IPN, Mexico City, Mexico
89,
R Lopez-Fernandez
R Lopez-Fernandez
89Centro de Investigacion y de Estudios Avanzados del IPN, Mexico City, Mexico
89,
J Mejia Guisao
J Mejia Guisao
89Centro de Investigacion y de Estudios Avanzados del IPN, Mexico City, Mexico
89,
R I Rabadan-Trejo
R I Rabadan-Trejo
89Centro de Investigacion y de Estudios Avanzados del IPN, Mexico City, Mexico
89,
G Ramirez-Sanchez
G Ramirez-Sanchez
89Centro de Investigacion y de Estudios Avanzados del IPN, Mexico City, Mexico
89,
R Reyes-Almanza
R Reyes-Almanza
89Centro de Investigacion y de Estudios Avanzados del IPN, Mexico City, Mexico
89,
A Sanchez-Hernandez
A Sanchez-Hernandez
89Centro de Investigacion y de Estudios Avanzados del IPN, Mexico City, Mexico
89,
S Carrillo Moreno
S Carrillo Moreno
90Universidad Iberoamericana, Mexico City, Mexico
90,
C Oropeza Barrera
C Oropeza Barrera
90Universidad Iberoamericana, Mexico City, Mexico
90,
F Vazquez Valencia
F Vazquez Valencia
90Universidad Iberoamericana, Mexico City, Mexico
90,
J Eysermans
J Eysermans
91Benemerita Universidad Autonoma de Puebla, Puebla, Mexico
91,
I Pedraza
I Pedraza
91Benemerita Universidad Autonoma de Puebla, Puebla, Mexico
91,
H A Salazar Ibarguen
H A Salazar Ibarguen
91Benemerita Universidad Autonoma de Puebla, Puebla, Mexico
91,
C Uribe Estrada
C Uribe Estrada
91Benemerita Universidad Autonoma de Puebla, Puebla, Mexico
91,
A Morelos Pineda
A Morelos Pineda
92Universidad Autónoma de San Luis Potosí, San Luis Potosí, Mexico
92,
D Krofcheck
D Krofcheck
93University of Auckland, Auckland, New Zealand
93,
S Bheesette
S Bheesette
94University of Canterbury, Christchurch, New Zealand
94,
P H Butler
P H Butler
94University of Canterbury, Christchurch, New Zealand
94,
A Ahmad
A Ahmad
95National Centre for Physics, Quaid-I-Azam University, Islamabad, Pakistan
95,
M Ahmad
M Ahmad
95National Centre for Physics, Quaid-I-Azam University, Islamabad, Pakistan
95,
M I Asghar
M I Asghar
95National Centre for Physics, Quaid-I-Azam University, Islamabad, Pakistan
95,
Q Hassan
Q Hassan
95National Centre for Physics, Quaid-I-Azam University, Islamabad, Pakistan
95,
H R Hoorani
H R Hoorani
95National Centre for Physics, Quaid-I-Azam University, Islamabad, Pakistan
95,
A Saddique
A Saddique
95National Centre for Physics, Quaid-I-Azam University, Islamabad, Pakistan
95,
M A Shah
M A Shah
95National Centre for Physics, Quaid-I-Azam University, Islamabad, Pakistan
95,
M Shoaib
M Shoaib
95National Centre for Physics, Quaid-I-Azam University, Islamabad, Pakistan
95,
M Waqas
M Waqas
95National Centre for Physics, Quaid-I-Azam University, Islamabad, Pakistan
95,
H Bialkowska
H Bialkowska
96National Centre for Nuclear Research, Swierk, Poland
96,
M Bluj
M Bluj
96National Centre for Nuclear Research, Swierk, Poland
96,
B Boimska
B Boimska
96National Centre for Nuclear Research, Swierk, Poland
96,
T Frueboes
T Frueboes
96National Centre for Nuclear Research, Swierk, Poland
96,
M Górski
M Górski
96National Centre for Nuclear Research, Swierk, Poland
96,
M Kazana
M Kazana
96National Centre for Nuclear Research, Swierk, Poland
96,
K Nawrocki
K Nawrocki
96National Centre for Nuclear Research, Swierk, Poland
96,
M Szleper
M Szleper
96National Centre for Nuclear Research, Swierk, Poland
96,
P Traczyk
P Traczyk
96National Centre for Nuclear Research, Swierk, Poland
96,
P Zalewski
P Zalewski
96National Centre for Nuclear Research, Swierk, Poland
96,
K Bunkowski
K Bunkowski
97Institute of Experimental Physics, Faculty of Physics, University of Warsaw, Warsaw, Poland
97,
A Byszuk
A Byszuk
97Institute of Experimental Physics, Faculty of Physics, University of Warsaw, Warsaw, Poland
97,
K Doroba
K Doroba
97Institute of Experimental Physics, Faculty of Physics, University of Warsaw, Warsaw, Poland
97,
A Kalinowski
A Kalinowski
97Institute of Experimental Physics, Faculty of Physics, University of Warsaw, Warsaw, Poland
97,
M Konecki
M Konecki
97Institute of Experimental Physics, Faculty of Physics, University of Warsaw, Warsaw, Poland
97,
J Krolikowski
J Krolikowski
97Institute of Experimental Physics, Faculty of Physics, University of Warsaw, Warsaw, Poland
97,
M Misiura
M Misiura
97Institute of Experimental Physics, Faculty of Physics, University of Warsaw, Warsaw, Poland
97,
M Olszewski
M Olszewski
97Institute of Experimental Physics, Faculty of Physics, University of Warsaw, Warsaw, Poland
97,
A Pyskir
A Pyskir
97Institute of Experimental Physics, Faculty of Physics, University of Warsaw, Warsaw, Poland
97,
M Walczak
M Walczak
97Institute of Experimental Physics, Faculty of Physics, University of Warsaw, Warsaw, Poland
97,
P Bargassa
P Bargassa
98Laboratório de Instrumentação e Física Experimental de Partículas, Lisbon, Portugal
98,
C Beirão Da Cruz E Silva
C Beirão Da Cruz E Silva
98Laboratório de Instrumentação e Física Experimental de Partículas, Lisbon, Portugal
98,
A Di Francesco
A Di Francesco
98Laboratório de Instrumentação e Física Experimental de Partículas, Lisbon, Portugal
98,
P Faccioli
P Faccioli
98Laboratório de Instrumentação e Física Experimental de Partículas, Lisbon, Portugal
98,
B Galinhas
B Galinhas
98Laboratório de Instrumentação e Física Experimental de Partículas, Lisbon, Portugal
98,
M Gallinaro
M Gallinaro
98Laboratório de Instrumentação e Física Experimental de Partículas, Lisbon, Portugal
98,
J Hollar
J Hollar
98Laboratório de Instrumentação e Física Experimental de Partículas, Lisbon, Portugal
98,
N Leonardo
N Leonardo
98Laboratório de Instrumentação e Física Experimental de Partículas, Lisbon, Portugal
98,
L Lloret Iglesias
L Lloret Iglesias
98Laboratório de Instrumentação e Física Experimental de Partículas, Lisbon, Portugal
98,
M V Nemallapudi
M V Nemallapudi
98Laboratório de Instrumentação e Física Experimental de Partículas, Lisbon, Portugal
98,
J Seixas
J Seixas
98Laboratório de Instrumentação e Física Experimental de Partículas, Lisbon, Portugal
98,
G Strong
G Strong
98Laboratório de Instrumentação e Física Experimental de Partículas, Lisbon, Portugal
98,
O Toldaiev
O Toldaiev
98Laboratório de Instrumentação e Física Experimental de Partículas, Lisbon, Portugal
98,
D Vadruccio
D Vadruccio
98Laboratório de Instrumentação e Física Experimental de Partículas, Lisbon, Portugal
98,
J Varela
J Varela
98Laboratório de Instrumentação e Física Experimental de Partículas, Lisbon, Portugal
98,
M Gavrilenko
M Gavrilenko
99Joint Institute for Nuclear Research, Dubna, Russia
99,
I Golutvin
I Golutvin
99Joint Institute for Nuclear Research, Dubna, Russia
99,
V Karjavin
V Karjavin
99Joint Institute for Nuclear Research, Dubna, Russia
99,
I Kashunin
I Kashunin
99Joint Institute for Nuclear Research, Dubna, Russia
99,
V Korenkov
V Korenkov
99Joint Institute for Nuclear Research, Dubna, Russia
99,
G Kozlov
G Kozlov
99Joint Institute for Nuclear Research, Dubna, Russia
99,
A Lanev
A Lanev
99Joint Institute for Nuclear Research, Dubna, Russia
99,
A Malakhov
A Malakhov
99Joint Institute for Nuclear Research, Dubna, Russia
99,
V Matveev
V Matveev
99Joint Institute for Nuclear Research, Dubna, Russia
99,
V V Mitsyn
V V Mitsyn
99Joint Institute for Nuclear Research, Dubna, Russia
99,
P Moisenz
P Moisenz
99Joint Institute for Nuclear Research, Dubna, Russia
99,
V Palichik
V Palichik
99Joint Institute for Nuclear Research, Dubna, Russia
99,
V Perelygin
V Perelygin
99Joint Institute for Nuclear Research, Dubna, Russia
99,
S Shmatov
S Shmatov
99Joint Institute for Nuclear Research, Dubna, Russia
99,
V Smirnov
V Smirnov
99Joint Institute for Nuclear Research, Dubna, Russia
99,
V Trofimov
V Trofimov
99Joint Institute for Nuclear Research, Dubna, Russia
99,
B S Yuldashev
B S Yuldashev
99Joint Institute for Nuclear Research, Dubna, Russia
99,
A Zarubin
A Zarubin
99Joint Institute for Nuclear Research, Dubna, Russia
99,
V Zhiltsov
V Zhiltsov
99Joint Institute for Nuclear Research, Dubna, Russia
99,
V Golovtsov
V Golovtsov
100Petersburg Nuclear Physics Institute, Gatchina (St. Petersburg), Russia
100,
Y Ivanov
Y Ivanov
100Petersburg Nuclear Physics Institute, Gatchina (St. Petersburg), Russia
100,
V Kim
V Kim
100Petersburg Nuclear Physics Institute, Gatchina (St. Petersburg), Russia
100,
E Kuznetsova
E Kuznetsova
100Petersburg Nuclear Physics Institute, Gatchina (St. Petersburg), Russia
100,
P Levchenko
P Levchenko
100Petersburg Nuclear Physics Institute, Gatchina (St. Petersburg), Russia
100,
V Murzin
V Murzin
100Petersburg Nuclear Physics Institute, Gatchina (St. Petersburg), Russia
100,
V Oreshkin
V Oreshkin
100Petersburg Nuclear Physics Institute, Gatchina (St. Petersburg), Russia
100,
I Smirnov
I Smirnov
100Petersburg Nuclear Physics Institute, Gatchina (St. Petersburg), Russia
100,
D Sosnov
D Sosnov
100Petersburg Nuclear Physics Institute, Gatchina (St. Petersburg), Russia
100,
V Sulimov
V Sulimov
100Petersburg Nuclear Physics Institute, Gatchina (St. Petersburg), Russia
100,
L Uvarov
L Uvarov
100Petersburg Nuclear Physics Institute, Gatchina (St. Petersburg), Russia
100,
S Vavilov
S Vavilov
100Petersburg Nuclear Physics Institute, Gatchina (St. Petersburg), Russia
100,
A Vorobyev
A Vorobyev
100Petersburg Nuclear Physics Institute, Gatchina (St. Petersburg), Russia
100,
Yu Andreev
Yu Andreev
101Institute for Nuclear Research, Moscow, Russia
101,
A Dermenev
A Dermenev
101Institute for Nuclear Research, Moscow, Russia
101,
S Gninenko
S Gninenko
101Institute for Nuclear Research, Moscow, Russia
101,
N Golubev
N Golubev
101Institute for Nuclear Research, Moscow, Russia
101,
A Karneyeu
A Karneyeu
101Institute for Nuclear Research, Moscow, Russia
101,
M Kirsanov
M Kirsanov
101Institute for Nuclear Research, Moscow, Russia
101,
N Krasnikov
N Krasnikov
101Institute for Nuclear Research, Moscow, Russia
101,
A Pashenkov
A Pashenkov
101Institute for Nuclear Research, Moscow, Russia
101,
D Tlisov
D Tlisov
101Institute for Nuclear Research, Moscow, Russia
101,
A Toropin
A Toropin
101Institute for Nuclear Research, Moscow, Russia
101,
V Epshteyn
V Epshteyn
102Institute for Theoretical and Experimental Physics, Moscow, Russia
102,
V Gavrilov
V Gavrilov
102Institute for Theoretical and Experimental Physics, Moscow, Russia
102,
N Lychkovskaya
N Lychkovskaya
102Institute for Theoretical and Experimental Physics, Moscow, Russia
102,
V Popov
V Popov
102Institute for Theoretical and Experimental Physics, Moscow, Russia
102,
I Pozdnyakov
I Pozdnyakov
102Institute for Theoretical and Experimental Physics, Moscow, Russia
102,
G Safronov
G Safronov
102Institute for Theoretical and Experimental Physics, Moscow, Russia
102,
A Spiridonov
A Spiridonov
102Institute for Theoretical and Experimental Physics, Moscow, Russia
102,
A Stepennov
A Stepennov
102Institute for Theoretical and Experimental Physics, Moscow, Russia
102,
V Stolin
V Stolin
102Institute for Theoretical and Experimental Physics, Moscow, Russia
102,
M Toms
M Toms
102Institute for Theoretical and Experimental Physics, Moscow, Russia
102,
E Vlasov
E Vlasov
102Institute for Theoretical and Experimental Physics, Moscow, Russia
102,
A Zhokin
A Zhokin
102Institute for Theoretical and Experimental Physics, Moscow, Russia
102,
T Aushev
T Aushev
103Moscow Institute of Physics and Technology, Moscow, Russia
103,
R Chistov
R Chistov
104National Research Nuclear University ‘Moscow Engineering Physics Institute’ (MEPhI), Moscow, Russia
104,
M Danilov
M Danilov
104National Research Nuclear University ‘Moscow Engineering Physics Institute’ (MEPhI), Moscow, Russia
104,
P Parygin
P Parygin
104National Research Nuclear University ‘Moscow Engineering Physics Institute’ (MEPhI), Moscow, Russia
104,
D Philippov
D Philippov
104National Research Nuclear University ‘Moscow Engineering Physics Institute’ (MEPhI), Moscow, Russia
104,
S Polikarpov
S Polikarpov
104National Research Nuclear University ‘Moscow Engineering Physics Institute’ (MEPhI), Moscow, Russia
104,
E Tarkovskii
E Tarkovskii
104National Research Nuclear University ‘Moscow Engineering Physics Institute’ (MEPhI), Moscow, Russia
104,
V Andreev
V Andreev
105P.N. Lebedev Physical Institute, Moscow, Russia
105,
M Azarkin
M Azarkin
105P.N. Lebedev Physical Institute, Moscow, Russia
105,
I Dremin
I Dremin
105P.N. Lebedev Physical Institute, Moscow, Russia
105,
M Kirakosyan
M Kirakosyan
105P.N. Lebedev Physical Institute, Moscow, Russia
105,
S V Rusakov
S V Rusakov
105P.N. Lebedev Physical Institute, Moscow, Russia
105,
A Terkulov
A Terkulov
105P.N. Lebedev Physical Institute, Moscow, Russia
105,
A Baskakov
A Baskakov
106Skobeltsyn Institute of Nuclear Physics, Lomonosov Moscow State University, Moscow, Russia
106,
A Belyaev
A Belyaev
106Skobeltsyn Institute of Nuclear Physics, Lomonosov Moscow State University, Moscow, Russia
106,
E Boos
E Boos
106Skobeltsyn Institute of Nuclear Physics, Lomonosov Moscow State University, Moscow, Russia
106,
V Bunichev
V Bunichev
106Skobeltsyn Institute of Nuclear Physics, Lomonosov Moscow State University, Moscow, Russia
106,
M Dubinin
M Dubinin
106Skobeltsyn Institute of Nuclear Physics, Lomonosov Moscow State University, Moscow, Russia
106,
L Dudko
L Dudko
106Skobeltsyn Institute of Nuclear Physics, Lomonosov Moscow State University, Moscow, Russia
106,
A Gribushin
A Gribushin
106Skobeltsyn Institute of Nuclear Physics, Lomonosov Moscow State University, Moscow, Russia
106,
V Klyukhin
V Klyukhin
106Skobeltsyn Institute of Nuclear Physics, Lomonosov Moscow State University, Moscow, Russia
106,
N Korneeva
N Korneeva
106Skobeltsyn Institute of Nuclear Physics, Lomonosov Moscow State University, Moscow, Russia
106,
I Lokhtin
I Lokhtin
106Skobeltsyn Institute of Nuclear Physics, Lomonosov Moscow State University, Moscow, Russia
106,
I Miagkov
I Miagkov
106Skobeltsyn Institute of Nuclear Physics, Lomonosov Moscow State University, Moscow, Russia
106,
S Obraztsov
S Obraztsov
106Skobeltsyn Institute of Nuclear Physics, Lomonosov Moscow State University, Moscow, Russia
106,
M Perfilov
M Perfilov
106Skobeltsyn Institute of Nuclear Physics, Lomonosov Moscow State University, Moscow, Russia
106,
V Savrin
V Savrin
106Skobeltsyn Institute of Nuclear Physics, Lomonosov Moscow State University, Moscow, Russia
106,
P Volkov
P Volkov
106Skobeltsyn Institute of Nuclear Physics, Lomonosov Moscow State University, Moscow, Russia
106,
V Blinov
V Blinov
107Novosibirsk State University (NSU), Novosibirsk, Russia
107,
T Dimova
T Dimova
107Novosibirsk State University (NSU), Novosibirsk, Russia
107,
L Kardapoltsev
L Kardapoltsev
107Novosibirsk State University (NSU), Novosibirsk, Russia
107,
D Shtol
D Shtol
107Novosibirsk State University (NSU), Novosibirsk, Russia
107,
Y Skovpen
Y Skovpen
107Novosibirsk State University (NSU), Novosibirsk, Russia
107,
I Azhgirey
I Azhgirey
108State Research Center of Russian Federation, Institute for High Energy Physics of NRC “Kurchatov Institute”, Protvino, Russia
108,
I Bayshev
I Bayshev
108State Research Center of Russian Federation, Institute for High Energy Physics of NRC “Kurchatov Institute”, Protvino, Russia
108,
S Bitioukov
S Bitioukov
108State Research Center of Russian Federation, Institute for High Energy Physics of NRC “Kurchatov Institute”, Protvino, Russia
108,
D Elumakhov
D Elumakhov
108State Research Center of Russian Federation, Institute for High Energy Physics of NRC “Kurchatov Institute”, Protvino, Russia
108,
A Godizov
A Godizov
108State Research Center of Russian Federation, Institute for High Energy Physics of NRC “Kurchatov Institute”, Protvino, Russia
108,
V Kachanov
V Kachanov
108State Research Center of Russian Federation, Institute for High Energy Physics of NRC “Kurchatov Institute”, Protvino, Russia
108,
A Kalinin
A Kalinin
108State Research Center of Russian Federation, Institute for High Energy Physics of NRC “Kurchatov Institute”, Protvino, Russia
108,
D Konstantinov
D Konstantinov
108State Research Center of Russian Federation, Institute for High Energy Physics of NRC “Kurchatov Institute”, Protvino, Russia
108,
P Mandrik
P Mandrik
108State Research Center of Russian Federation, Institute for High Energy Physics of NRC “Kurchatov Institute”, Protvino, Russia
108,
V Petrov
V Petrov
108State Research Center of Russian Federation, Institute for High Energy Physics of NRC “Kurchatov Institute”, Protvino, Russia
108,
R Ryutin
R Ryutin
108State Research Center of Russian Federation, Institute for High Energy Physics of NRC “Kurchatov Institute”, Protvino, Russia
108,
S Slabospitskii
S Slabospitskii
108State Research Center of Russian Federation, Institute for High Energy Physics of NRC “Kurchatov Institute”, Protvino, Russia
108,
A Sobol
A Sobol
108State Research Center of Russian Federation, Institute for High Energy Physics of NRC “Kurchatov Institute”, Protvino, Russia
108,
S Troshin
S Troshin
108State Research Center of Russian Federation, Institute for High Energy Physics of NRC “Kurchatov Institute”, Protvino, Russia
108,
N Tyurin
N Tyurin
108State Research Center of Russian Federation, Institute for High Energy Physics of NRC “Kurchatov Institute”, Protvino, Russia
108,
A Uzunian
A Uzunian
108State Research Center of Russian Federation, Institute for High Energy Physics of NRC “Kurchatov Institute”, Protvino, Russia
108,
A Volkov
A Volkov
108State Research Center of Russian Federation, Institute for High Energy Physics of NRC “Kurchatov Institute”, Protvino, Russia
108,
A Babaev
A Babaev
109National Research Tomsk Polytechnic University, Tomsk, Russia
109,
S Baidali
S Baidali
109National Research Tomsk Polytechnic University, Tomsk, Russia
109,
P Adzic
P Adzic
110Faculty of Physics and Vinca Institute of Nuclear Sciences, University of Belgrade, Belgrade, Serbia
110,
P Cirkovic
P Cirkovic
110Faculty of Physics and Vinca Institute of Nuclear Sciences, University of Belgrade, Belgrade, Serbia
110,
D Devetak
D Devetak
110Faculty of Physics and Vinca Institute of Nuclear Sciences, University of Belgrade, Belgrade, Serbia
110,
M Dordevic
M Dordevic
110Faculty of Physics and Vinca Institute of Nuclear Sciences, University of Belgrade, Belgrade, Serbia
110,
J Milosevic
J Milosevic
110Faculty of Physics and Vinca Institute of Nuclear Sciences, University of Belgrade, Belgrade, Serbia
110,
J Alcaraz Maestre
J Alcaraz Maestre
111Centro de Investigaciones Energéticas Medioambientales y Tecnológicas (CIEMAT), Madrid, Spain
111,
A Álvarez Fernández
A Álvarez Fernández
111Centro de Investigaciones Energéticas Medioambientales y Tecnológicas (CIEMAT), Madrid, Spain
111,
I Bachiller
I Bachiller
111Centro de Investigaciones Energéticas Medioambientales y Tecnológicas (CIEMAT), Madrid, Spain
111,
M Barrio Luna
M Barrio Luna
111Centro de Investigaciones Energéticas Medioambientales y Tecnológicas (CIEMAT), Madrid, Spain
111,
J A Brochero Cifuentes
J A Brochero Cifuentes
111Centro de Investigaciones Energéticas Medioambientales y Tecnológicas (CIEMAT), Madrid, Spain
111,
M Cerrada
M Cerrada
111Centro de Investigaciones Energéticas Medioambientales y Tecnológicas (CIEMAT), Madrid, Spain
111,
N Colino
N Colino
111Centro de Investigaciones Energéticas Medioambientales y Tecnológicas (CIEMAT), Madrid, Spain
111,
B De La Cruz
B De La Cruz
111Centro de Investigaciones Energéticas Medioambientales y Tecnológicas (CIEMAT), Madrid, Spain
111,
A Delgado Peris
A Delgado Peris
111Centro de Investigaciones Energéticas Medioambientales y Tecnológicas (CIEMAT), Madrid, Spain
111,
C Fernandez Bedoya
C Fernandez Bedoya
111Centro de Investigaciones Energéticas Medioambientales y Tecnológicas (CIEMAT), Madrid, Spain
111,
J P Fernández Ramos
J P Fernández Ramos
111Centro de Investigaciones Energéticas Medioambientales y Tecnológicas (CIEMAT), Madrid, Spain
111,
J Flix
J Flix
111Centro de Investigaciones Energéticas Medioambientales y Tecnológicas (CIEMAT), Madrid, Spain
111,
M C Fouz
M C Fouz
111Centro de Investigaciones Energéticas Medioambientales y Tecnológicas (CIEMAT), Madrid, Spain
111,
O Gonzalez Lopez
O Gonzalez Lopez
111Centro de Investigaciones Energéticas Medioambientales y Tecnológicas (CIEMAT), Madrid, Spain
111,
S Goy Lopez
S Goy Lopez
111Centro de Investigaciones Energéticas Medioambientales y Tecnológicas (CIEMAT), Madrid, Spain
111,
J M Hernandez
J M Hernandez
111Centro de Investigaciones Energéticas Medioambientales y Tecnológicas (CIEMAT), Madrid, Spain
111,
M I Josa
M I Josa
111Centro de Investigaciones Energéticas Medioambientales y Tecnológicas (CIEMAT), Madrid, Spain
111,
D Moran
D Moran
111Centro de Investigaciones Energéticas Medioambientales y Tecnológicas (CIEMAT), Madrid, Spain
111,
A Pérez-Calero Yzquierdo
A Pérez-Calero Yzquierdo
111Centro de Investigaciones Energéticas Medioambientales y Tecnológicas (CIEMAT), Madrid, Spain
111,
J Puerta Pelayo
J Puerta Pelayo
111Centro de Investigaciones Energéticas Medioambientales y Tecnológicas (CIEMAT), Madrid, Spain
111,
I Redondo
I Redondo
111Centro de Investigaciones Energéticas Medioambientales y Tecnológicas (CIEMAT), Madrid, Spain
111,
L Romero
L Romero
111Centro de Investigaciones Energéticas Medioambientales y Tecnológicas (CIEMAT), Madrid, Spain
111,
M S Soares
M S Soares
111Centro de Investigaciones Energéticas Medioambientales y Tecnológicas (CIEMAT), Madrid, Spain
111,
A Triossi
A Triossi
111Centro de Investigaciones Energéticas Medioambientales y Tecnológicas (CIEMAT), Madrid, Spain
111,
C Albajar
C Albajar
112Universidad Autónoma de Madrid, Madrid, Spain
112,
J F de Trocóniz
J F de Trocóniz
112Universidad Autónoma de Madrid, Madrid, Spain
112,
J Cuevas
J Cuevas
113Universidad de Oviedo, Oviedo, Spain
113,
C Erice
C Erice
113Universidad de Oviedo, Oviedo, Spain
113,
J Fernandez Menendez
J Fernandez Menendez
113Universidad de Oviedo, Oviedo, Spain
113,
S Folgueras
S Folgueras
113Universidad de Oviedo, Oviedo, Spain
113,
I Gonzalez Caballero
I Gonzalez Caballero
113Universidad de Oviedo, Oviedo, Spain
113,
J R González Fernández
J R González Fernández
113Universidad de Oviedo, Oviedo, Spain
113,
E Palencia Cortezon
E Palencia Cortezon
113Universidad de Oviedo, Oviedo, Spain
113,
V Rodríguez Bouza
V Rodríguez Bouza
113Universidad de Oviedo, Oviedo, Spain
113,
S Sanchez Cruz
S Sanchez Cruz
113Universidad de Oviedo, Oviedo, Spain
113,
P Vischia
P Vischia
113Universidad de Oviedo, Oviedo, Spain
113,
J M Vizan Garcia
J M Vizan Garcia
113Universidad de Oviedo, Oviedo, Spain
113,
I J Cabrillo
I J Cabrillo
114Instituto de Física de Cantabria (IFCA), CSIC-Universidad de Cantabria, Santander, Spain
114,
A Calderon
A Calderon
114Instituto de Física de Cantabria (IFCA), CSIC-Universidad de Cantabria, Santander, Spain
114,
B Chazin Quero
B Chazin Quero
114Instituto de Física de Cantabria (IFCA), CSIC-Universidad de Cantabria, Santander, Spain
114,
J Duarte Campderros
J Duarte Campderros
114Instituto de Física de Cantabria (IFCA), CSIC-Universidad de Cantabria, Santander, Spain
114,
M Fernandez
M Fernandez
114Instituto de Física de Cantabria (IFCA), CSIC-Universidad de Cantabria, Santander, Spain
114,
P J Fernández Manteca
P J Fernández Manteca
114Instituto de Física de Cantabria (IFCA), CSIC-Universidad de Cantabria, Santander, Spain
114,
A García Alonso
A García Alonso
114Instituto de Física de Cantabria (IFCA), CSIC-Universidad de Cantabria, Santander, Spain
114,
J Garcia-Ferrero
J Garcia-Ferrero
114Instituto de Física de Cantabria (IFCA), CSIC-Universidad de Cantabria, Santander, Spain
114,
G Gomez
G Gomez
114Instituto de Física de Cantabria (IFCA), CSIC-Universidad de Cantabria, Santander, Spain
114,
A Lopez Virto
A Lopez Virto
114Instituto de Física de Cantabria (IFCA), CSIC-Universidad de Cantabria, Santander, Spain
114,
J Marco
J Marco
114Instituto de Física de Cantabria (IFCA), CSIC-Universidad de Cantabria, Santander, Spain
114,
C Martinez Rivero
C Martinez Rivero
114Instituto de Física de Cantabria (IFCA), CSIC-Universidad de Cantabria, Santander, Spain
114,
P Martinez Ruiz del Arbol
P Martinez Ruiz del Arbol
114Instituto de Física de Cantabria (IFCA), CSIC-Universidad de Cantabria, Santander, Spain
114,
F Matorras
F Matorras
114Instituto de Física de Cantabria (IFCA), CSIC-Universidad de Cantabria, Santander, Spain
114,
J Piedra Gomez
J Piedra Gomez
114Instituto de Física de Cantabria (IFCA), CSIC-Universidad de Cantabria, Santander, Spain
114,
C Prieels
C Prieels
114Instituto de Física de Cantabria (IFCA), CSIC-Universidad de Cantabria, Santander, Spain
114,
T Rodrigo
T Rodrigo
114Instituto de Física de Cantabria (IFCA), CSIC-Universidad de Cantabria, Santander, Spain
114,
A Ruiz-Jimeno
A Ruiz-Jimeno
114Instituto de Física de Cantabria (IFCA), CSIC-Universidad de Cantabria, Santander, Spain
114,
L Scodellaro
L Scodellaro
114Instituto de Física de Cantabria (IFCA), CSIC-Universidad de Cantabria, Santander, Spain
114,
N Trevisani
N Trevisani
114Instituto de Física de Cantabria (IFCA), CSIC-Universidad de Cantabria, Santander, Spain
114,
I Vila
I Vila
114Instituto de Física de Cantabria (IFCA), CSIC-Universidad de Cantabria, Santander, Spain
114,
R Vilar Cortabitarte
R Vilar Cortabitarte
114Instituto de Física de Cantabria (IFCA), CSIC-Universidad de Cantabria, Santander, Spain
114,
D Abbaneo
D Abbaneo
115CERN, European Organization for Nuclear Research, Geneva, Switzerland
115,
B Akgun
B Akgun
115CERN, European Organization for Nuclear Research, Geneva, Switzerland
115,
E Auffray
E Auffray
115CERN, European Organization for Nuclear Research, Geneva, Switzerland
115,
P Baillon
P Baillon
115CERN, European Organization for Nuclear Research, Geneva, Switzerland
115,
A H Ball
A H Ball
115CERN, European Organization for Nuclear Research, Geneva, Switzerland
115,
D Barney
D Barney
115CERN, European Organization for Nuclear Research, Geneva, Switzerland
115,
J Bendavid
J Bendavid
115CERN, European Organization for Nuclear Research, Geneva, Switzerland
115,
M Bianco
M Bianco
115CERN, European Organization for Nuclear Research, Geneva, Switzerland
115,
A Bocci
A Bocci
115CERN, European Organization for Nuclear Research, Geneva, Switzerland
115,
C Botta
C Botta
115CERN, European Organization for Nuclear Research, Geneva, Switzerland
115,
T Camporesi
T Camporesi
115CERN, European Organization for Nuclear Research, Geneva, Switzerland
115,
M Cepeda
M Cepeda
115CERN, European Organization for Nuclear Research, Geneva, Switzerland
115,
G Cerminara
G Cerminara
115CERN, European Organization for Nuclear Research, Geneva, Switzerland
115,
E Chapon
E Chapon
115CERN, European Organization for Nuclear Research, Geneva, Switzerland
115,
Y Chen
Y Chen
115CERN, European Organization for Nuclear Research, Geneva, Switzerland
115,
G Cucciati
G Cucciati
115CERN, European Organization for Nuclear Research, Geneva, Switzerland
115,
D d’Enterria
D d’Enterria
115CERN, European Organization for Nuclear Research, Geneva, Switzerland
115,
A Dabrowski
A Dabrowski
115CERN, European Organization for Nuclear Research, Geneva, Switzerland
115,
V Daponte
V Daponte
115CERN, European Organization for Nuclear Research, Geneva, Switzerland
115,
A David
A David
115CERN, European Organization for Nuclear Research, Geneva, Switzerland
115,
A De Roeck
A De Roeck
115CERN, European Organization for Nuclear Research, Geneva, Switzerland
115,
N Deelen
N Deelen
115CERN, European Organization for Nuclear Research, Geneva, Switzerland
115,
M Dobson
M Dobson
115CERN, European Organization for Nuclear Research, Geneva, Switzerland
115,
T du Pree
T du Pree
115CERN, European Organization for Nuclear Research, Geneva, Switzerland
115,
M Dünser
M Dünser
115CERN, European Organization for Nuclear Research, Geneva, Switzerland
115,
N Dupont
N Dupont
115CERN, European Organization for Nuclear Research, Geneva, Switzerland
115,
A Elliott-Peisert
A Elliott-Peisert
115CERN, European Organization for Nuclear Research, Geneva, Switzerland
115,
P Everaerts
P Everaerts
115CERN, European Organization for Nuclear Research, Geneva, Switzerland
115,
F Fallavollita
F Fallavollita
115CERN, European Organization for Nuclear Research, Geneva, Switzerland
115,
D Fasanella
D Fasanella
115CERN, European Organization for Nuclear Research, Geneva, Switzerland
115,
G Franzoni
G Franzoni
115CERN, European Organization for Nuclear Research, Geneva, Switzerland
115,
J Fulcher
J Fulcher
115CERN, European Organization for Nuclear Research, Geneva, Switzerland
115,
W Funk
W Funk
115CERN, European Organization for Nuclear Research, Geneva, Switzerland
115,
D Gigi
D Gigi
115CERN, European Organization for Nuclear Research, Geneva, Switzerland
115,
A Gilbert
A Gilbert
115CERN, European Organization for Nuclear Research, Geneva, Switzerland
115,
K Gill
K Gill
115CERN, European Organization for Nuclear Research, Geneva, Switzerland
115,
F Glege
F Glege
115CERN, European Organization for Nuclear Research, Geneva, Switzerland
115,
M Guilbaud
M Guilbaud
115CERN, European Organization for Nuclear Research, Geneva, Switzerland
115,
D Gulhan
D Gulhan
115CERN, European Organization for Nuclear Research, Geneva, Switzerland
115,
J Hegeman
J Hegeman
115CERN, European Organization for Nuclear Research, Geneva, Switzerland
115,
V Innocente
V Innocente
115CERN, European Organization for Nuclear Research, Geneva, Switzerland
115,
A Jafari
A Jafari
115CERN, European Organization for Nuclear Research, Geneva, Switzerland
115,
P Janot
P Janot
115CERN, European Organization for Nuclear Research, Geneva, Switzerland
115,
O Karacheban
O Karacheban
115CERN, European Organization for Nuclear Research, Geneva, Switzerland
115,
J Kieseler
J Kieseler
115CERN, European Organization for Nuclear Research, Geneva, Switzerland
115,
A Kornmayer
A Kornmayer
115CERN, European Organization for Nuclear Research, Geneva, Switzerland
115,
M Krammer
M Krammer
115CERN, European Organization for Nuclear Research, Geneva, Switzerland
115,
C Lange
C Lange
115CERN, European Organization for Nuclear Research, Geneva, Switzerland
115,
P Lecoq
P Lecoq
115CERN, European Organization for Nuclear Research, Geneva, Switzerland
115,
C Lourenço
C Lourenço
115CERN, European Organization for Nuclear Research, Geneva, Switzerland
115,
L Malgeri
L Malgeri
115CERN, European Organization for Nuclear Research, Geneva, Switzerland
115,
M Mannelli
M Mannelli
115CERN, European Organization for Nuclear Research, Geneva, Switzerland
115,
F Meijers
F Meijers
115CERN, European Organization for Nuclear Research, Geneva, Switzerland
115,
J A Merlin
J A Merlin
115CERN, European Organization for Nuclear Research, Geneva, Switzerland
115,
S Mersi
S Mersi
115CERN, European Organization for Nuclear Research, Geneva, Switzerland
115,
E Meschi
E Meschi
115CERN, European Organization for Nuclear Research, Geneva, Switzerland
115,
P Milenovic
P Milenovic
115CERN, European Organization for Nuclear Research, Geneva, Switzerland
115,
F Moortgat
F Moortgat
115CERN, European Organization for Nuclear Research, Geneva, Switzerland
115,
M Mulders
M Mulders
115CERN, European Organization for Nuclear Research, Geneva, Switzerland
115,
J Ngadiuba
J Ngadiuba
115CERN, European Organization for Nuclear Research, Geneva, Switzerland
115,
S Orfanelli
S Orfanelli
115CERN, European Organization for Nuclear Research, Geneva, Switzerland
115,
L Orsini
L Orsini
115CERN, European Organization for Nuclear Research, Geneva, Switzerland
115,
F Pantaleo
F Pantaleo
115CERN, European Organization for Nuclear Research, Geneva, Switzerland
115,
L Pape
L Pape
115CERN, European Organization for Nuclear Research, Geneva, Switzerland
115,
E Perez
E Perez
115CERN, European Organization for Nuclear Research, Geneva, Switzerland
115,
M Peruzzi
M Peruzzi
115CERN, European Organization for Nuclear Research, Geneva, Switzerland
115,
A Petrilli
A Petrilli
115CERN, European Organization for Nuclear Research, Geneva, Switzerland
115,
G Petrucciani
G Petrucciani
115CERN, European Organization for Nuclear Research, Geneva, Switzerland
115,
A Pfeiffer
A Pfeiffer
115CERN, European Organization for Nuclear Research, Geneva, Switzerland
115,
M Pierini
M Pierini
115CERN, European Organization for Nuclear Research, Geneva, Switzerland
115,
F M Pitters
F M Pitters
115CERN, European Organization for Nuclear Research, Geneva, Switzerland
115,
D Rabady
D Rabady
115CERN, European Organization for Nuclear Research, Geneva, Switzerland
115,
A Racz
A Racz
115CERN, European Organization for Nuclear Research, Geneva, Switzerland
115,
T Reis
T Reis
115CERN, European Organization for Nuclear Research, Geneva, Switzerland
115,
G Rolandi
G Rolandi
115CERN, European Organization for Nuclear Research, Geneva, Switzerland
115,
M Rovere
M Rovere
115CERN, European Organization for Nuclear Research, Geneva, Switzerland
115,
H Sakulin
H Sakulin
115CERN, European Organization for Nuclear Research, Geneva, Switzerland
115,
C Schäfer
C Schäfer
115CERN, European Organization for Nuclear Research, Geneva, Switzerland
115,
C Schwick
C Schwick
115CERN, European Organization for Nuclear Research, Geneva, Switzerland
115,
M Seidel
M Seidel
115CERN, European Organization for Nuclear Research, Geneva, Switzerland
115,
M Selvaggi
M Selvaggi
115CERN, European Organization for Nuclear Research, Geneva, Switzerland
115,
A Sharma
A Sharma
115CERN, European Organization for Nuclear Research, Geneva, Switzerland
115,
P Silva
P Silva
115CERN, European Organization for Nuclear Research, Geneva, Switzerland
115,
P Sphicas
P Sphicas
115CERN, European Organization for Nuclear Research, Geneva, Switzerland
115,
A Stakia
A Stakia
115CERN, European Organization for Nuclear Research, Geneva, Switzerland
115,
J Steggemann
J Steggemann
115CERN, European Organization for Nuclear Research, Geneva, Switzerland
115,
M Tosi
M Tosi
115CERN, European Organization for Nuclear Research, Geneva, Switzerland
115,
D Treille
D Treille
115CERN, European Organization for Nuclear Research, Geneva, Switzerland
115,
A Tsirou
A Tsirou
115CERN, European Organization for Nuclear Research, Geneva, Switzerland
115,
V Veckalns
V Veckalns
115CERN, European Organization for Nuclear Research, Geneva, Switzerland
115,
W D Zeuner
W D Zeuner
115CERN, European Organization for Nuclear Research, Geneva, Switzerland
115,
L Caminada
L Caminada
116Paul Scherrer Institut, Villigen, Switzerland
116,
K Deiters
K Deiters
116Paul Scherrer Institut, Villigen, Switzerland
116,
W Erdmann
W Erdmann
116Paul Scherrer Institut, Villigen, Switzerland
116,
R Horisberger
R Horisberger
116Paul Scherrer Institut, Villigen, Switzerland
116,
Q Ingram
Q Ingram
116Paul Scherrer Institut, Villigen, Switzerland
116,
H C Kaestli
H C Kaestli
116Paul Scherrer Institut, Villigen, Switzerland
116,
D Kotlinski
D Kotlinski
116Paul Scherrer Institut, Villigen, Switzerland
116,
U Langenegger
U Langenegger
116Paul Scherrer Institut, Villigen, Switzerland
116,
T Rohe
T Rohe
116Paul Scherrer Institut, Villigen, Switzerland
116,
S A Wiederkehr
S A Wiederkehr
116Paul Scherrer Institut, Villigen, Switzerland
116,
M Backhaus
M Backhaus
117ETH Zurich-Institute for Particle Physics and Astrophysics (IPA), Zurich, Switzerland
117,
L Bäni
L Bäni
117ETH Zurich-Institute for Particle Physics and Astrophysics (IPA), Zurich, Switzerland
117,
P Berger
P Berger
117ETH Zurich-Institute for Particle Physics and Astrophysics (IPA), Zurich, Switzerland
117,
N Chernyavskaya
N Chernyavskaya
117ETH Zurich-Institute for Particle Physics and Astrophysics (IPA), Zurich, Switzerland
117,
G Dissertori
G Dissertori
117ETH Zurich-Institute for Particle Physics and Astrophysics (IPA), Zurich, Switzerland
117,
M Dittmar
M Dittmar
117ETH Zurich-Institute for Particle Physics and Astrophysics (IPA), Zurich, Switzerland
117,
M Donegà
M Donegà
117ETH Zurich-Institute for Particle Physics and Astrophysics (IPA), Zurich, Switzerland
117,
C Dorfer
C Dorfer
117ETH Zurich-Institute for Particle Physics and Astrophysics (IPA), Zurich, Switzerland
117,
C Grab
C Grab
117ETH Zurich-Institute for Particle Physics and Astrophysics (IPA), Zurich, Switzerland
117,
C Heidegger
C Heidegger
117ETH Zurich-Institute for Particle Physics and Astrophysics (IPA), Zurich, Switzerland
117,
D Hits
D Hits
117ETH Zurich-Institute for Particle Physics and Astrophysics (IPA), Zurich, Switzerland
117,
J Hoss
J Hoss
117ETH Zurich-Institute for Particle Physics and Astrophysics (IPA), Zurich, Switzerland
117,
T Klijnsma
T Klijnsma
117ETH Zurich-Institute for Particle Physics and Astrophysics (IPA), Zurich, Switzerland
117,
W Lustermann
W Lustermann
117ETH Zurich-Institute for Particle Physics and Astrophysics (IPA), Zurich, Switzerland
117,
R A Manzoni
R A Manzoni
117ETH Zurich-Institute for Particle Physics and Astrophysics (IPA), Zurich, Switzerland
117,
M Marionneau
M Marionneau
117ETH Zurich-Institute for Particle Physics and Astrophysics (IPA), Zurich, Switzerland
117,
M T Meinhard
M T Meinhard
117ETH Zurich-Institute for Particle Physics and Astrophysics (IPA), Zurich, Switzerland
117,
F Micheli
F Micheli
117ETH Zurich-Institute for Particle Physics and Astrophysics (IPA), Zurich, Switzerland
117,
P Musella
P Musella
117ETH Zurich-Institute for Particle Physics and Astrophysics (IPA), Zurich, Switzerland
117,
F Nessi-Tedaldi
F Nessi-Tedaldi
117ETH Zurich-Institute for Particle Physics and Astrophysics (IPA), Zurich, Switzerland
117,
J Pata
J Pata
117ETH Zurich-Institute for Particle Physics and Astrophysics (IPA), Zurich, Switzerland
117,
F Pauss
F Pauss
117ETH Zurich-Institute for Particle Physics and Astrophysics (IPA), Zurich, Switzerland
117,
G Perrin
G Perrin
117ETH Zurich-Institute for Particle Physics and Astrophysics (IPA), Zurich, Switzerland
117,
L Perrozzi
L Perrozzi
117ETH Zurich-Institute for Particle Physics and Astrophysics (IPA), Zurich, Switzerland
117,
S Pigazzini
S Pigazzini
117ETH Zurich-Institute for Particle Physics and Astrophysics (IPA), Zurich, Switzerland
117,
M Quittnat
M Quittnat
117ETH Zurich-Institute for Particle Physics and Astrophysics (IPA), Zurich, Switzerland
117,
D Ruini
D Ruini
117ETH Zurich-Institute for Particle Physics and Astrophysics (IPA), Zurich, Switzerland
117,
D A Sanz Becerra
D A Sanz Becerra
117ETH Zurich-Institute for Particle Physics and Astrophysics (IPA), Zurich, Switzerland
117,
M Schönenberger
M Schönenberger
117ETH Zurich-Institute for Particle Physics and Astrophysics (IPA), Zurich, Switzerland
117,
L Shchutska
L Shchutska
117ETH Zurich-Institute for Particle Physics and Astrophysics (IPA), Zurich, Switzerland
117,
V R Tavolaro
V R Tavolaro
117ETH Zurich-Institute for Particle Physics and Astrophysics (IPA), Zurich, Switzerland
117,
K Theofilatos
K Theofilatos
117ETH Zurich-Institute for Particle Physics and Astrophysics (IPA), Zurich, Switzerland
117,
M L Vesterbacka Olsson
M L Vesterbacka Olsson
117ETH Zurich-Institute for Particle Physics and Astrophysics (IPA), Zurich, Switzerland
117,
R Wallny
R Wallny
117ETH Zurich-Institute for Particle Physics and Astrophysics (IPA), Zurich, Switzerland
117,
D H Zhu
D H Zhu
117ETH Zurich-Institute for Particle Physics and Astrophysics (IPA), Zurich, Switzerland
117,
T K Aarrestad
T K Aarrestad
118Universität Zürich, Zurich, Switzerland
118,
C Amsler
C Amsler
118Universität Zürich, Zurich, Switzerland
118,
D Brzhechko
D Brzhechko
118Universität Zürich, Zurich, Switzerland
118,
M F Canelli
M F Canelli
118Universität Zürich, Zurich, Switzerland
118,
A De Cosa
A De Cosa
118Universität Zürich, Zurich, Switzerland
118,
R Del Burgo
R Del Burgo
118Universität Zürich, Zurich, Switzerland
118,
S Donato
S Donato
118Universität Zürich, Zurich, Switzerland
118,
C Galloni
C Galloni
118Universität Zürich, Zurich, Switzerland
118,
T Hreus
T Hreus
118Universität Zürich, Zurich, Switzerland
118,
B Kilminster
B Kilminster
118Universität Zürich, Zurich, Switzerland
118,
I Neutelings
I Neutelings
118Universität Zürich, Zurich, Switzerland
118,
D Pinna
D Pinna
118Universität Zürich, Zurich, Switzerland
118,
G Rauco
G Rauco
118Universität Zürich, Zurich, Switzerland
118,
P Robmann
P Robmann
118Universität Zürich, Zurich, Switzerland
118,
D Salerno
D Salerno
118Universität Zürich, Zurich, Switzerland
118,
K Schweiger
K Schweiger
118Universität Zürich, Zurich, Switzerland
118,
C Seitz
C Seitz
118Universität Zürich, Zurich, Switzerland
118,
Y Takahashi
Y Takahashi
118Universität Zürich, Zurich, Switzerland
118,
A Zucchetta
A Zucchetta
118Universität Zürich, Zurich, Switzerland
118,
Y H Chang
Y H Chang
119National Central University, Chung-Li, Taiwan
119,
K y Cheng
K y Cheng
119National Central University, Chung-Li, Taiwan
119,
T H Doan
T H Doan
119National Central University, Chung-Li, Taiwan
119,
Sh Jain
Sh Jain
119National Central University, Chung-Li, Taiwan
119,
R Khurana
R Khurana
119National Central University, Chung-Li, Taiwan
119,
C M Kuo
C M Kuo
119National Central University, Chung-Li, Taiwan
119,
W Lin
W Lin
119National Central University, Chung-Li, Taiwan
119,
A Pozdnyakov
A Pozdnyakov
119National Central University, Chung-Li, Taiwan
119,
S S Yu
S S Yu
119National Central University, Chung-Li, Taiwan
119,
P Chang
P Chang
120National Taiwan University (NTU), Taipei, Taiwan
120,
Y Chao
Y Chao
120National Taiwan University (NTU), Taipei, Taiwan
120,
K F Chen
K F Chen
120National Taiwan University (NTU), Taipei, Taiwan
120,
P H Chen
P H Chen
120National Taiwan University (NTU), Taipei, Taiwan
120,
W-S Hou
W-S Hou
120National Taiwan University (NTU), Taipei, Taiwan
120,
Arun Kumar
Arun Kumar
120National Taiwan University (NTU), Taipei, Taiwan
120,
Y y Li
Y y Li
120National Taiwan University (NTU), Taipei, Taiwan
120,
R-S Lu
R-S Lu
120National Taiwan University (NTU), Taipei, Taiwan
120,
E Paganis
E Paganis
120National Taiwan University (NTU), Taipei, Taiwan
120,
A Psallidas
A Psallidas
120National Taiwan University (NTU), Taipei, Taiwan
120,
A Steen
A Steen
120National Taiwan University (NTU), Taipei, Taiwan
120,
J f Tsai
J f Tsai
120National Taiwan University (NTU), Taipei, Taiwan
120,
B Asavapibhop
B Asavapibhop
121Faculty of Science, Department of Physics, Chulalongkorn University, Bangkok, Thailand
121,
N Srimanobhas
N Srimanobhas
121Faculty of Science, Department of Physics, Chulalongkorn University, Bangkok, Thailand
121,
N Suwonjandee
N Suwonjandee
121Faculty of Science, Department of Physics, Chulalongkorn University, Bangkok, Thailand
121,
M N Bakirci
M N Bakirci
122Physics Department, Science and Art Faculty, Çukurova University, Adana, Turkey
122,
A Bat
A Bat
122Physics Department, Science and Art Faculty, Çukurova University, Adana, Turkey
122,
F Boran
F Boran
122Physics Department, Science and Art Faculty, Çukurova University, Adana, Turkey
122,
S Damarseckin
S Damarseckin
122Physics Department, Science and Art Faculty, Çukurova University, Adana, Turkey
122,
Z S Demiroglu
Z S Demiroglu
122Physics Department, Science and Art Faculty, Çukurova University, Adana, Turkey
122,
F Dolek
F Dolek
122Physics Department, Science and Art Faculty, Çukurova University, Adana, Turkey
122,
C Dozen
C Dozen
122Physics Department, Science and Art Faculty, Çukurova University, Adana, Turkey
122,
S Girgis
S Girgis
122Physics Department, Science and Art Faculty, Çukurova University, Adana, Turkey
122,
G Gokbulut
G Gokbulut
122Physics Department, Science and Art Faculty, Çukurova University, Adana, Turkey
122,
Y Guler
Y Guler
122Physics Department, Science and Art Faculty, Çukurova University, Adana, Turkey
122,
E Gurpinar
E Gurpinar
122Physics Department, Science and Art Faculty, Çukurova University, Adana, Turkey
122,
I Hos
I Hos
122Physics Department, Science and Art Faculty, Çukurova University, Adana, Turkey
122,
C Isik
C Isik
122Physics Department, Science and Art Faculty, Çukurova University, Adana, Turkey
122,
E E Kangal
E E Kangal
122Physics Department, Science and Art Faculty, Çukurova University, Adana, Turkey
122,
O Kara
O Kara
122Physics Department, Science and Art Faculty, Çukurova University, Adana, Turkey
122,
A Kayis Topaksu
A Kayis Topaksu
122Physics Department, Science and Art Faculty, Çukurova University, Adana, Turkey
122,
U Kiminsu
U Kiminsu
122Physics Department, Science and Art Faculty, Çukurova University, Adana, Turkey
122,
M Oglakci
M Oglakci
122Physics Department, Science and Art Faculty, Çukurova University, Adana, Turkey
122,
G Onengut
G Onengut
122Physics Department, Science and Art Faculty, Çukurova University, Adana, Turkey
122,
K Ozdemir
K Ozdemir
122Physics Department, Science and Art Faculty, Çukurova University, Adana, Turkey
122,
S Ozturk
S Ozturk
122Physics Department, Science and Art Faculty, Çukurova University, Adana, Turkey
122,
D Sunar Cerci
D Sunar Cerci
122Physics Department, Science and Art Faculty, Çukurova University, Adana, Turkey
122,
B Tali
B Tali
122Physics Department, Science and Art Faculty, Çukurova University, Adana, Turkey
122,
U G Tok
U G Tok
122Physics Department, Science and Art Faculty, Çukurova University, Adana, Turkey
122,
H Topakli
H Topakli
122Physics Department, Science and Art Faculty, Çukurova University, Adana, Turkey
122,
S Turkcapar
S Turkcapar
122Physics Department, Science and Art Faculty, Çukurova University, Adana, Turkey
122,
I S Zorbakir
I S Zorbakir
122Physics Department, Science and Art Faculty, Çukurova University, Adana, Turkey
122,
C Zorbilmez
C Zorbilmez
122Physics Department, Science and Art Faculty, Çukurova University, Adana, Turkey
122,
B Isildak
B Isildak
123Middle East Technical University, Physics Department, Ankara, Turkey
123,
G Karapinar
G Karapinar
123Middle East Technical University, Physics Department, Ankara, Turkey
123,
M Yalvac
M Yalvac
123Middle East Technical University, Physics Department, Ankara, Turkey
123,
M Zeyrek
M Zeyrek
123Middle East Technical University, Physics Department, Ankara, Turkey
123,
I O Atakisi
I O Atakisi
124Bogazici University, Istanbul, Turkey
124,
E Gülmez
E Gülmez
124Bogazici University, Istanbul, Turkey
124,
M Kaya
M Kaya
124Bogazici University, Istanbul, Turkey
124,
O Kaya
O Kaya
124Bogazici University, Istanbul, Turkey
124,
S Tekten
S Tekten
124Bogazici University, Istanbul, Turkey
124,
E A Yetkin
E A Yetkin
124Bogazici University, Istanbul, Turkey
124,
M N Agaras
M N Agaras
125Istanbul Technical University, Istanbul, Turkey
125,
S Atay
S Atay
125Istanbul Technical University, Istanbul, Turkey
125,
A Cakir
A Cakir
125Istanbul Technical University, Istanbul, Turkey
125,
K Cankocak
K Cankocak
125Istanbul Technical University, Istanbul, Turkey
125,
Y Komurcu
Y Komurcu
125Istanbul Technical University, Istanbul, Turkey
125,
S Sen
S Sen
125Istanbul Technical University, Istanbul, Turkey
125,
B Grynyov
B Grynyov
126Institute for Scintillation Materials of National Academy of Science of Ukraine, Kharkov, Ukraine
126,
L Levchuk
L Levchuk
127National Scientific Center, Kharkov Institute of Physics and Technology, Kharkov, Ukraine
127,
F Ball
F Ball
128University of Bristol, Bristol, UK
128,
L Beck
L Beck
128University of Bristol, Bristol, UK
128,
J J Brooke
J J Brooke
128University of Bristol, Bristol, UK
128,
D Burns
D Burns
128University of Bristol, Bristol, UK
128,
E Clement
E Clement
128University of Bristol, Bristol, UK
128,
D Cussans
D Cussans
128University of Bristol, Bristol, UK
128,
O Davignon
O Davignon
128University of Bristol, Bristol, UK
128,
H Flacher
H Flacher
128University of Bristol, Bristol, UK
128,
J Goldstein
J Goldstein
128University of Bristol, Bristol, UK
128,
G P Heath
G P Heath
128University of Bristol, Bristol, UK
128,
H F Heath
H F Heath
128University of Bristol, Bristol, UK
128,
L Kreczko
L Kreczko
128University of Bristol, Bristol, UK
128,
D M Newbold
D M Newbold
128University of Bristol, Bristol, UK
128,
S Paramesvaran
S Paramesvaran
128University of Bristol, Bristol, UK
128,
B Penning
B Penning
128University of Bristol, Bristol, UK
128,
T Sakuma
T Sakuma
128University of Bristol, Bristol, UK
128,
D Smith
D Smith
128University of Bristol, Bristol, UK
128,
V J Smith
V J Smith
128University of Bristol, Bristol, UK
128,
J Taylor
J Taylor
128University of Bristol, Bristol, UK
128,
A Titterton
A Titterton
128University of Bristol, Bristol, UK
128,
K W Bell
K W Bell
129Rutherford Appleton Laboratory, Didcot, UK
129,
A Belyaev
A Belyaev
129Rutherford Appleton Laboratory, Didcot, UK
129,
C Brew
C Brew
129Rutherford Appleton Laboratory, Didcot, UK
129,
R M Brown
R M Brown
129Rutherford Appleton Laboratory, Didcot, UK
129,
D Cieri
D Cieri
129Rutherford Appleton Laboratory, Didcot, UK
129,
D J A Cockerill
D J A Cockerill
129Rutherford Appleton Laboratory, Didcot, UK
129,
J A Coughlan
J A Coughlan
129Rutherford Appleton Laboratory, Didcot, UK
129,
K Harder
K Harder
129Rutherford Appleton Laboratory, Didcot, UK
129,
S Harper
S Harper
129Rutherford Appleton Laboratory, Didcot, UK
129,
J Linacre
J Linacre
129Rutherford Appleton Laboratory, Didcot, UK
129,
E Olaiya
E Olaiya
129Rutherford Appleton Laboratory, Didcot, UK
129,
D Petyt
D Petyt
129Rutherford Appleton Laboratory, Didcot, UK
129,
C H Shepherd-Themistocleous
C H Shepherd-Themistocleous
129Rutherford Appleton Laboratory, Didcot, UK
129,
A Thea
A Thea
129Rutherford Appleton Laboratory, Didcot, UK
129,
I R Tomalin
I R Tomalin
129Rutherford Appleton Laboratory, Didcot, UK
129,
T Williams
T Williams
129Rutherford Appleton Laboratory, Didcot, UK
129,
W J Womersley
W J Womersley
129Rutherford Appleton Laboratory, Didcot, UK
129,
G Auzinger
G Auzinger
130Imperial College, London, UK
130,
R Bainbridge
R Bainbridge
130Imperial College, London, UK
130,
P Bloch
P Bloch
130Imperial College, London, UK
130,
J Borg
J Borg
130Imperial College, London, UK
130,
S Breeze
S Breeze
130Imperial College, London, UK
130,
O Buchmuller
O Buchmuller
130Imperial College, London, UK
130,
A Bundock
A Bundock
130Imperial College, London, UK
130,
S Casasso
S Casasso
130Imperial College, London, UK
130,
D Colling
D Colling
130Imperial College, London, UK
130,
L Corpe
L Corpe
130Imperial College, London, UK
130,
P Dauncey
P Dauncey
130Imperial College, London, UK
130,
G Davies
G Davies
130Imperial College, London, UK
130,
M Della Negra
M Della Negra
130Imperial College, London, UK
130,
R Di Maria
R Di Maria
130Imperial College, London, UK
130,
Y Haddad
Y Haddad
130Imperial College, London, UK
130,
G Hall
G Hall
130Imperial College, London, UK
130,
G Iles
G Iles
130Imperial College, London, UK
130,
T James
T James
130Imperial College, London, UK
130,
M Komm
M Komm
130Imperial College, London, UK
130,
C Laner
C Laner
130Imperial College, London, UK
130,
L Lyons
L Lyons
130Imperial College, London, UK
130,
A-M Magnan
A-M Magnan
130Imperial College, London, UK
130,
S Malik
S Malik
130Imperial College, London, UK
130,
A Martelli
A Martelli
130Imperial College, London, UK
130,
J Nash
J Nash
130Imperial College, London, UK
130,
A Nikitenko
A Nikitenko
130Imperial College, London, UK
130,
V Palladino
V Palladino
130Imperial College, London, UK
130,
M Pesaresi
M Pesaresi
130Imperial College, London, UK
130,
A Richards
A Richards
130Imperial College, London, UK
130,
A Rose
A Rose
130Imperial College, London, UK
130,
E Scott
E Scott
130Imperial College, London, UK
130,
C Seez
C Seez
130Imperial College, London, UK
130,
A Shtipliyski
A Shtipliyski
130Imperial College, London, UK
130,
T Strebler
T Strebler
130Imperial College, London, UK
130,
S Summers
S Summers
130Imperial College, London, UK
130,
A Tapper
A Tapper
130Imperial College, London, UK
130,
K Uchida
K Uchida
130Imperial College, London, UK
130,
T Virdee
T Virdee
130Imperial College, London, UK
130,
N Wardle
N Wardle
130Imperial College, London, UK
130,
D Winterbottom
D Winterbottom
130Imperial College, London, UK
130,
J Wright
J Wright
130Imperial College, London, UK
130,
S C Zenz
S C Zenz
130Imperial College, London, UK
130,
J E Cole
J E Cole
131Brunel University, Uxbridge, UK
131,
P R Hobson
P R Hobson
131Brunel University, Uxbridge, UK
131,
A Khan
A Khan
131Brunel University, Uxbridge, UK
131,
P Kyberd
P Kyberd
131Brunel University, Uxbridge, UK
131,
C K Mackay
C K Mackay
131Brunel University, Uxbridge, UK
131,
A Morton
A Morton
131Brunel University, Uxbridge, UK
131,
I D Reid
I D Reid
131Brunel University, Uxbridge, UK
131,
L Teodorescu
L Teodorescu
131Brunel University, Uxbridge, UK
131,
S Zahid
S Zahid
131Brunel University, Uxbridge, UK
131,
K Call
K Call
132Baylor University, Waco, USA
132,
J Dittmann
J Dittmann
132Baylor University, Waco, USA
132,
K Hatakeyama
K Hatakeyama
132Baylor University, Waco, USA
132,
H Liu
H Liu
132Baylor University, Waco, USA
132,
C Madrid
C Madrid
132Baylor University, Waco, USA
132,
B Mcmaster
B Mcmaster
132Baylor University, Waco, USA
132,
N Pastika
N Pastika
132Baylor University, Waco, USA
132,
C Smith
C Smith
132Baylor University, Waco, USA
132,
R Bartek
R Bartek
133Catholic University of America, Washington, DC, USA
133,
A Dominguez
A Dominguez
133Catholic University of America, Washington, DC, USA
133,
A Buccilli
A Buccilli
134The University of Alabama, Tuscaloosa, USA
134,
S I Cooper
S I Cooper
134The University of Alabama, Tuscaloosa, USA
134,
C Henderson
C Henderson
134The University of Alabama, Tuscaloosa, USA
134,
P Rumerio
P Rumerio
134The University of Alabama, Tuscaloosa, USA
134,
C West
C West
134The University of Alabama, Tuscaloosa, USA
134,
D Arcaro
D Arcaro
135Boston University, Boston, USA
135,
T Bose
T Bose
135Boston University, Boston, USA
135,
D Gastler
D Gastler
135Boston University, Boston, USA
135,
D Rankin
D Rankin
135Boston University, Boston, USA
135,
C Richardson
C Richardson
135Boston University, Boston, USA
135,
J Rohlf
J Rohlf
135Boston University, Boston, USA
135,
L Sulak
L Sulak
135Boston University, Boston, USA
135,
D Zou
D Zou
135Boston University, Boston, USA
135,
G Benelli
G Benelli
136Brown University, Providence, USA
136,
X Coubez
X Coubez
136Brown University, Providence, USA
136,
D Cutts
D Cutts
136Brown University, Providence, USA
136,
M Hadley
M Hadley
136Brown University, Providence, USA
136,
J Hakala
J Hakala
136Brown University, Providence, USA
136,
U Heintz
U Heintz
136Brown University, Providence, USA
136,
J M Hogan
J M Hogan
136Brown University, Providence, USA
136,
K H M Kwok
K H M Kwok
136Brown University, Providence, USA
136,
E Laird
E Laird
136Brown University, Providence, USA
136,
G Landsberg
G Landsberg
136Brown University, Providence, USA
136,
J Lee
J Lee
136Brown University, Providence, USA
136,
Z Mao
Z Mao
136Brown University, Providence, USA
136,
M Narain
M Narain
136Brown University, Providence, USA
136,
J Pazzini
J Pazzini
136Brown University, Providence, USA
136,
S Piperov
S Piperov
136Brown University, Providence, USA
136,
S Sagir
S Sagir
136Brown University, Providence, USA
136,
R Syarif
R Syarif
136Brown University, Providence, USA
136,
E Usai
E Usai
136Brown University, Providence, USA
136,
D Yu
D Yu
136Brown University, Providence, USA
136,
R Band
R Band
137University of California, Davis, Davis, USA
137,
C Brainerd
C Brainerd
137University of California, Davis, Davis, USA
137,
R Breedon
R Breedon
137University of California, Davis, Davis, USA
137,
D Burns
D Burns
137University of California, Davis, Davis, USA
137,
M Calderon De La Barca Sanchez
M Calderon De La Barca Sanchez
137University of California, Davis, Davis, USA
137,
M Chertok
M Chertok
137University of California, Davis, Davis, USA
137,
J Conway
J Conway
137University of California, Davis, Davis, USA
137,
R Conway
R Conway
137University of California, Davis, Davis, USA
137,
P T Cox
P T Cox
137University of California, Davis, Davis, USA
137,
R Erbacher
R Erbacher
137University of California, Davis, Davis, USA
137,
C Flores
C Flores
137University of California, Davis, Davis, USA
137,
G Funk
G Funk
137University of California, Davis, Davis, USA
137,
W Ko
W Ko
137University of California, Davis, Davis, USA
137,
O Kukral
O Kukral
137University of California, Davis, Davis, USA
137,
R Lander
R Lander
137University of California, Davis, Davis, USA
137,
C Mclean
C Mclean
137University of California, Davis, Davis, USA
137,
M Mulhearn
M Mulhearn
137University of California, Davis, Davis, USA
137,
D Pellett
D Pellett
137University of California, Davis, Davis, USA
137,
J Pilot
J Pilot
137University of California, Davis, Davis, USA
137,
S Shalhout
S Shalhout
137University of California, Davis, Davis, USA
137,
M Shi
M Shi
137University of California, Davis, Davis, USA
137,
D Stolp
D Stolp
137University of California, Davis, Davis, USA
137,
D Taylor
D Taylor
137University of California, Davis, Davis, USA
137,
K Tos
K Tos
137University of California, Davis, Davis, USA
137,
M Tripathi
M Tripathi
137University of California, Davis, Davis, USA
137,
Z Wang
Z Wang
137University of California, Davis, Davis, USA
137,
M Bachtis
M Bachtis
138University of California, Los Angeles, USA
138,
C Bravo
C Bravo
138University of California, Los Angeles, USA
138,
R Cousins
R Cousins
138University of California, Los Angeles, USA
138,
A Dasgupta
A Dasgupta
138University of California, Los Angeles, USA
138,
A Florent
A Florent
138University of California, Los Angeles, USA
138,
J Hauser
J Hauser
138University of California, Los Angeles, USA
138,
M Ignatenko
M Ignatenko
138University of California, Los Angeles, USA
138,
N Mccoll
N Mccoll
138University of California, Los Angeles, USA
138,
S Regnard
S Regnard
138University of California, Los Angeles, USA
138,
D Saltzberg
D Saltzberg
138University of California, Los Angeles, USA
138,
C Schnaible
C Schnaible
138University of California, Los Angeles, USA
138,
V Valuev
V Valuev
138University of California, Los Angeles, USA
138,
E Bouvier
E Bouvier
139University of California, Riverside, Riverside, USA
139,
K Burt
K Burt
139University of California, Riverside, Riverside, USA
139,
R Clare
R Clare
139University of California, Riverside, Riverside, USA
139,
J W Gary
J W Gary
139University of California, Riverside, Riverside, USA
139,
S M A Ghiasi Shirazi
S M A Ghiasi Shirazi
139University of California, Riverside, Riverside, USA
139,
G Hanson
G Hanson
139University of California, Riverside, Riverside, USA
139,
G Karapostoli
G Karapostoli
139University of California, Riverside, Riverside, USA
139,
E Kennedy
E Kennedy
139University of California, Riverside, Riverside, USA
139,
F Lacroix
F Lacroix
139University of California, Riverside, Riverside, USA
139,
O R Long
O R Long
139University of California, Riverside, Riverside, USA
139,
M Olmedo Negrete
M Olmedo Negrete
139University of California, Riverside, Riverside, USA
139,
M I Paneva
M I Paneva
139University of California, Riverside, Riverside, USA
139,
W Si
W Si
139University of California, Riverside, Riverside, USA
139,
L Wang
L Wang
139University of California, Riverside, Riverside, USA
139,
H Wei
H Wei
139University of California, Riverside, Riverside, USA
139,
S Wimpenny
S Wimpenny
139University of California, Riverside, Riverside, USA
139,
B R Yates
B R Yates
139University of California, Riverside, Riverside, USA
139,
J G Branson
J G Branson
140University of California, San Diego, La Jolla, USA
140,
S Cittolin
S Cittolin
140University of California, San Diego, La Jolla, USA
140,
M Derdzinski
M Derdzinski
140University of California, San Diego, La Jolla, USA
140,
R Gerosa
R Gerosa
140University of California, San Diego, La Jolla, USA
140,
D Gilbert
D Gilbert
140University of California, San Diego, La Jolla, USA
140,
B Hashemi
B Hashemi
140University of California, San Diego, La Jolla, USA
140,
A Holzner
A Holzner
140University of California, San Diego, La Jolla, USA
140,
D Klein
D Klein
140University of California, San Diego, La Jolla, USA
140,
G Kole
G Kole
140University of California, San Diego, La Jolla, USA
140,
V Krutelyov
V Krutelyov
140University of California, San Diego, La Jolla, USA
140,
J Letts
J Letts
140University of California, San Diego, La Jolla, USA
140,
M Masciovecchio
M Masciovecchio
140University of California, San Diego, La Jolla, USA
140,
D Olivito
D Olivito
140University of California, San Diego, La Jolla, USA
140,
S Padhi
S Padhi
140University of California, San Diego, La Jolla, USA
140,
M Pieri
M Pieri
140University of California, San Diego, La Jolla, USA
140,
M Sani
M Sani
140University of California, San Diego, La Jolla, USA
140,
V Sharma
V Sharma
140University of California, San Diego, La Jolla, USA
140,
S Simon
S Simon
140University of California, San Diego, La Jolla, USA
140,
M Tadel
M Tadel
140University of California, San Diego, La Jolla, USA
140,
A Vartak
A Vartak
140University of California, San Diego, La Jolla, USA
140,
S Wasserbaech
S Wasserbaech
140University of California, San Diego, La Jolla, USA
140,
J Wood
J Wood
140University of California, San Diego, La Jolla, USA
140,
F Würthwein
F Würthwein
140University of California, San Diego, La Jolla, USA
140,
A Yagil
A Yagil
140University of California, San Diego, La Jolla, USA
140,
G Zevi Della Porta
G Zevi Della Porta
140University of California, San Diego, La Jolla, USA
140,
N Amin
N Amin
141Department of Physics, University of California, Santa Barbara, Santa Barbara, USA
141,
R Bhandari
R Bhandari
141Department of Physics, University of California, Santa Barbara, Santa Barbara, USA
141,
J Bradmiller-Feld
J Bradmiller-Feld
141Department of Physics, University of California, Santa Barbara, Santa Barbara, USA
141,
C Campagnari
C Campagnari
141Department of Physics, University of California, Santa Barbara, Santa Barbara, USA
141,
M Citron
M Citron
141Department of Physics, University of California, Santa Barbara, Santa Barbara, USA
141,
A Dishaw
A Dishaw
141Department of Physics, University of California, Santa Barbara, Santa Barbara, USA
141,
V Dutta
V Dutta
141Department of Physics, University of California, Santa Barbara, Santa Barbara, USA
141,
M Franco Sevilla
M Franco Sevilla
141Department of Physics, University of California, Santa Barbara, Santa Barbara, USA
141,
L Gouskos
L Gouskos
141Department of Physics, University of California, Santa Barbara, Santa Barbara, USA
141,
R Heller
R Heller
141Department of Physics, University of California, Santa Barbara, Santa Barbara, USA
141,
J Incandela
J Incandela
141Department of Physics, University of California, Santa Barbara, Santa Barbara, USA
141,
A Ovcharova
A Ovcharova
141Department of Physics, University of California, Santa Barbara, Santa Barbara, USA
141,
H Qu
H Qu
141Department of Physics, University of California, Santa Barbara, Santa Barbara, USA
141,
J Richman
J Richman
141Department of Physics, University of California, Santa Barbara, Santa Barbara, USA
141,
D Stuart
D Stuart
141Department of Physics, University of California, Santa Barbara, Santa Barbara, USA
141,
I Suarez
I Suarez
141Department of Physics, University of California, Santa Barbara, Santa Barbara, USA
141,
S Wang
S Wang
141Department of Physics, University of California, Santa Barbara, Santa Barbara, USA
141,
J Yoo
J Yoo
141Department of Physics, University of California, Santa Barbara, Santa Barbara, USA
141,
D Anderson
D Anderson
142California Institute of Technology, Pasadena, USA
142,
A Bornheim
A Bornheim
142California Institute of Technology, Pasadena, USA
142,
J M Lawhorn
J M Lawhorn
142California Institute of Technology, Pasadena, USA
142,
H B Newman
H B Newman
142California Institute of Technology, Pasadena, USA
142,
T Q Nguyen
T Q Nguyen
142California Institute of Technology, Pasadena, USA
142,
M Spiropulu
M Spiropulu
142California Institute of Technology, Pasadena, USA
142,
J R Vlimant
J R Vlimant
142California Institute of Technology, Pasadena, USA
142,
R Wilkinson
R Wilkinson
142California Institute of Technology, Pasadena, USA
142,
S Xie
S Xie
142California Institute of Technology, Pasadena, USA
142,
Z Zhang
Z Zhang
142California Institute of Technology, Pasadena, USA
142,
R Y Zhu
R Y Zhu
142California Institute of Technology, Pasadena, USA
142,
M B Andrews
M B Andrews
143Carnegie Mellon University, Pittsburgh, USA
143,
T Ferguson
T Ferguson
143Carnegie Mellon University, Pittsburgh, USA
143,
T Mudholkar
T Mudholkar
143Carnegie Mellon University, Pittsburgh, USA
143,
M Paulini
M Paulini
143Carnegie Mellon University, Pittsburgh, USA
143,
M Sun
M Sun
143Carnegie Mellon University, Pittsburgh, USA
143,
I Vorobiev
I Vorobiev
143Carnegie Mellon University, Pittsburgh, USA
143,
M Weinberg
M Weinberg
143Carnegie Mellon University, Pittsburgh, USA
143,
J P Cumalat
J P Cumalat
144University of Colorado Boulder, Boulder, USA
144,
W T Ford
W T Ford
144University of Colorado Boulder, Boulder, USA
144,
F Jensen
F Jensen
144University of Colorado Boulder, Boulder, USA
144,
A Johnson
A Johnson
144University of Colorado Boulder, Boulder, USA
144,
M Krohn
M Krohn
144University of Colorado Boulder, Boulder, USA
144,
S Leontsinis
S Leontsinis
144University of Colorado Boulder, Boulder, USA
144,
E MacDonald
E MacDonald
144University of Colorado Boulder, Boulder, USA
144,
T Mulholland
T Mulholland
144University of Colorado Boulder, Boulder, USA
144,
K Stenson
K Stenson
144University of Colorado Boulder, Boulder, USA
144,
K A Ulmer
K A Ulmer
144University of Colorado Boulder, Boulder, USA
144,
S R Wagner
S R Wagner
144University of Colorado Boulder, Boulder, USA
144,
J Alexander
J Alexander
145Cornell University, Ithaca, USA
145,
J Chaves
J Chaves
145Cornell University, Ithaca, USA
145,
Y Cheng
Y Cheng
145Cornell University, Ithaca, USA
145,
J Chu
J Chu
145Cornell University, Ithaca, USA
145,
A Datta
A Datta
145Cornell University, Ithaca, USA
145,
K Mcdermott
K Mcdermott
145Cornell University, Ithaca, USA
145,
N Mirman
N Mirman
145Cornell University, Ithaca, USA
145,
J R Patterson
J R Patterson
145Cornell University, Ithaca, USA
145,
D Quach
D Quach
145Cornell University, Ithaca, USA
145,
A Rinkevicius
A Rinkevicius
145Cornell University, Ithaca, USA
145,
A Ryd
A Ryd
145Cornell University, Ithaca, USA
145,
L Skinnari
L Skinnari
145Cornell University, Ithaca, USA
145,
L Soffi
L Soffi
145Cornell University, Ithaca, USA
145,
S M Tan
S M Tan
145Cornell University, Ithaca, USA
145,
Z Tao
Z Tao
145Cornell University, Ithaca, USA
145,
J Thom
J Thom
145Cornell University, Ithaca, USA
145,
J Tucker
J Tucker
145Cornell University, Ithaca, USA
145,
P Wittich
P Wittich
145Cornell University, Ithaca, USA
145,
M Zientek
M Zientek
145Cornell University, Ithaca, USA
145,
S Abdullin
S Abdullin
146Fermi National Accelerator Laboratory, Batavia, USA
146,
M Albrow
M Albrow
146Fermi National Accelerator Laboratory, Batavia, USA
146,
M Alyari
M Alyari
146Fermi National Accelerator Laboratory, Batavia, USA
146,
G Apollinari
G Apollinari
146Fermi National Accelerator Laboratory, Batavia, USA
146,
A Apresyan
A Apresyan
146Fermi National Accelerator Laboratory, Batavia, USA
146,
A Apyan
A Apyan
146Fermi National Accelerator Laboratory, Batavia, USA
146,
S Banerjee
S Banerjee
146Fermi National Accelerator Laboratory, Batavia, USA
146,
L A T Bauerdick
L A T Bauerdick
146Fermi National Accelerator Laboratory, Batavia, USA
146,
A Beretvas
A Beretvas
146Fermi National Accelerator Laboratory, Batavia, USA
146,
J Berryhill
J Berryhill
146Fermi National Accelerator Laboratory, Batavia, USA
146,
P C Bhat
P C Bhat
146Fermi National Accelerator Laboratory, Batavia, USA
146,
G Bolla
G Bolla
146Fermi National Accelerator Laboratory, Batavia, USA
146,
K Burkett
K Burkett
146Fermi National Accelerator Laboratory, Batavia, USA
146,
J N Butler
J N Butler
146Fermi National Accelerator Laboratory, Batavia, USA
146,
A Canepa
A Canepa
146Fermi National Accelerator Laboratory, Batavia, USA
146,
G B Cerati
G B Cerati
146Fermi National Accelerator Laboratory, Batavia, USA
146,
H W K Cheung
H W K Cheung
146Fermi National Accelerator Laboratory, Batavia, USA
146,
F Chlebana
F Chlebana
146Fermi National Accelerator Laboratory, Batavia, USA
146,
M Cremonesi
M Cremonesi
146Fermi National Accelerator Laboratory, Batavia, USA
146,
J Duarte
J Duarte
146Fermi National Accelerator Laboratory, Batavia, USA
146,
V D Elvira
V D Elvira
146Fermi National Accelerator Laboratory, Batavia, USA
146,
J Freeman
J Freeman
146Fermi National Accelerator Laboratory, Batavia, USA
146,
Z Gecse
Z Gecse
146Fermi National Accelerator Laboratory, Batavia, USA
146,
E Gottschalk
E Gottschalk
146Fermi National Accelerator Laboratory, Batavia, USA
146,
L Gray
L Gray
146Fermi National Accelerator Laboratory, Batavia, USA
146,
D Green
D Green
146Fermi National Accelerator Laboratory, Batavia, USA
146,
S Grünendahl
S Grünendahl
146Fermi National Accelerator Laboratory, Batavia, USA
146,
O Gutsche
O Gutsche
146Fermi National Accelerator Laboratory, Batavia, USA
146,
J Hanlon
J Hanlon
146Fermi National Accelerator Laboratory, Batavia, USA
146,
R M Harris
R M Harris
146Fermi National Accelerator Laboratory, Batavia, USA
146,
S Hasegawa
S Hasegawa
146Fermi National Accelerator Laboratory, Batavia, USA
146,
J Hirschauer
J Hirschauer
146Fermi National Accelerator Laboratory, Batavia, USA
146,
Z Hu
Z Hu
146Fermi National Accelerator Laboratory, Batavia, USA
146,
B Jayatilaka
B Jayatilaka
146Fermi National Accelerator Laboratory, Batavia, USA
146,
S Jindariani
S Jindariani
146Fermi National Accelerator Laboratory, Batavia, USA
146,
M Johnson
M Johnson
146Fermi National Accelerator Laboratory, Batavia, USA
146,
U Joshi
U Joshi
146Fermi National Accelerator Laboratory, Batavia, USA
146,
B Klima
B Klima
146Fermi National Accelerator Laboratory, Batavia, USA
146,
M J Kortelainen
M J Kortelainen
146Fermi National Accelerator Laboratory, Batavia, USA
146,
B Kreis
B Kreis
146Fermi National Accelerator Laboratory, Batavia, USA
146,
S Lammel
S Lammel
146Fermi National Accelerator Laboratory, Batavia, USA
146,
D Lincoln
D Lincoln
146Fermi National Accelerator Laboratory, Batavia, USA
146,
R Lipton
R Lipton
146Fermi National Accelerator Laboratory, Batavia, USA
146,
M Liu
M Liu
146Fermi National Accelerator Laboratory, Batavia, USA
146,
T Liu
T Liu
146Fermi National Accelerator Laboratory, Batavia, USA
146,
J Lykken
J Lykken
146Fermi National Accelerator Laboratory, Batavia, USA
146,
K Maeshima
K Maeshima
146Fermi National Accelerator Laboratory, Batavia, USA
146,
J M Marraffino
J M Marraffino
146Fermi National Accelerator Laboratory, Batavia, USA
146,
D Mason
D Mason
146Fermi National Accelerator Laboratory, Batavia, USA
146,
P McBride
P McBride
146Fermi National Accelerator Laboratory, Batavia, USA
146,
P Merkel
P Merkel
146Fermi National Accelerator Laboratory, Batavia, USA
146,
S Mrenna
S Mrenna
146Fermi National Accelerator Laboratory, Batavia, USA
146,
S Nahn
S Nahn
146Fermi National Accelerator Laboratory, Batavia, USA
146,
V O’Dell
V O’Dell
146Fermi National Accelerator Laboratory, Batavia, USA
146,
K Pedro
K Pedro
146Fermi National Accelerator Laboratory, Batavia, USA
146,
O Prokofyev
O Prokofyev
146Fermi National Accelerator Laboratory, Batavia, USA
146,
G Rakness
G Rakness
146Fermi National Accelerator Laboratory, Batavia, USA
146,
L Ristori
L Ristori
146Fermi National Accelerator Laboratory, Batavia, USA
146,
A Savoy-Navarro
A Savoy-Navarro
146Fermi National Accelerator Laboratory, Batavia, USA
146,
B Schneider
B Schneider
146Fermi National Accelerator Laboratory, Batavia, USA
146,
E Sexton-Kennedy
E Sexton-Kennedy
146Fermi National Accelerator Laboratory, Batavia, USA
146,
A Soha
A Soha
146Fermi National Accelerator Laboratory, Batavia, USA
146,
W J Spalding
W J Spalding
146Fermi National Accelerator Laboratory, Batavia, USA
146,
L Spiegel
L Spiegel
146Fermi National Accelerator Laboratory, Batavia, USA
146,
S Stoynev
S Stoynev
146Fermi National Accelerator Laboratory, Batavia, USA
146,
J Strait
J Strait
146Fermi National Accelerator Laboratory, Batavia, USA
146,
N Strobbe
N Strobbe
146Fermi National Accelerator Laboratory, Batavia, USA
146,
L Taylor
L Taylor
146Fermi National Accelerator Laboratory, Batavia, USA
146,
S Tkaczyk
S Tkaczyk
146Fermi National Accelerator Laboratory, Batavia, USA
146,
N V Tran
N V Tran
146Fermi National Accelerator Laboratory, Batavia, USA
146,
L Uplegger
L Uplegger
146Fermi National Accelerator Laboratory, Batavia, USA
146,
E W Vaandering
E W Vaandering
146Fermi National Accelerator Laboratory, Batavia, USA
146,
C Vernieri
C Vernieri
146Fermi National Accelerator Laboratory, Batavia, USA
146,
M Verzocchi
M Verzocchi
146Fermi National Accelerator Laboratory, Batavia, USA
146,
R Vidal
R Vidal
146Fermi National Accelerator Laboratory, Batavia, USA
146,
M Wang
M Wang
146Fermi National Accelerator Laboratory, Batavia, USA
146,
H A Weber
H A Weber
146Fermi National Accelerator Laboratory, Batavia, USA
146,
A Whitbeck
A Whitbeck
146Fermi National Accelerator Laboratory, Batavia, USA
146,
D Acosta
D Acosta
147University of Florida, Gainesville, USA
147,
P Avery
P Avery
147University of Florida, Gainesville, USA
147,
P Bortignon
P Bortignon
147University of Florida, Gainesville, USA
147,
D Bourilkov
D Bourilkov
147University of Florida, Gainesville, USA
147,
A Brinkerhoff
A Brinkerhoff
147University of Florida, Gainesville, USA
147,
L Cadamuro
L Cadamuro
147University of Florida, Gainesville, USA
147,
A Carnes
A Carnes
147University of Florida, Gainesville, USA
147,
M Carver
M Carver
147University of Florida, Gainesville, USA
147,
D Curry
D Curry
147University of Florida, Gainesville, USA
147,
R D Field
R D Field
147University of Florida, Gainesville, USA
147,
S V Gleyzer
S V Gleyzer
147University of Florida, Gainesville, USA
147,
B M Joshi
B M Joshi
147University of Florida, Gainesville, USA
147,
J Konigsberg
J Konigsberg
147University of Florida, Gainesville, USA
147,
A Korytov
A Korytov
147University of Florida, Gainesville, USA
147,
P Ma
P Ma
147University of Florida, Gainesville, USA
147,
K Matchev
K Matchev
147University of Florida, Gainesville, USA
147,
H Mei
H Mei
147University of Florida, Gainesville, USA
147,
G Mitselmakher
G Mitselmakher
147University of Florida, Gainesville, USA
147,
K Shi
K Shi
147University of Florida, Gainesville, USA
147,
D Sperka
D Sperka
147University of Florida, Gainesville, USA
147,
J Wang
J Wang
147University of Florida, Gainesville, USA
147,
S Wang
S Wang
147University of Florida, Gainesville, USA
147,
Y R Joshi
Y R Joshi
148Florida International University, Miami, USA
148,
S Linn
S Linn
148Florida International University, Miami, USA
148,
A Ackert
A Ackert
149Florida State University, Tallahassee, USA
149,
T Adams
T Adams
149Florida State University, Tallahassee, USA
149,
A Askew
A Askew
149Florida State University, Tallahassee, USA
149,
S Hagopian
S Hagopian
149Florida State University, Tallahassee, USA
149,
V Hagopian
V Hagopian
149Florida State University, Tallahassee, USA
149,
K F Johnson
K F Johnson
149Florida State University, Tallahassee, USA
149,
T Kolberg
T Kolberg
149Florida State University, Tallahassee, USA
149,
G Martinez
G Martinez
149Florida State University, Tallahassee, USA
149,
T Perry
T Perry
149Florida State University, Tallahassee, USA
149,
H Prosper
H Prosper
149Florida State University, Tallahassee, USA
149,
A Saha
A Saha
149Florida State University, Tallahassee, USA
149,
A Santra
A Santra
149Florida State University, Tallahassee, USA
149,
V Sharma
V Sharma
149Florida State University, Tallahassee, USA
149,
R Yohay
R Yohay
149Florida State University, Tallahassee, USA
149,
M M Baarmand
M M Baarmand
150Florida Institute of Technology, Melbourne, USA
150,
V Bhopatkar
V Bhopatkar
150Florida Institute of Technology, Melbourne, USA
150,
S Colafranceschi
S Colafranceschi
150Florida Institute of Technology, Melbourne, USA
150,
M Hohlmann
M Hohlmann
150Florida Institute of Technology, Melbourne, USA
150,
D Noonan
D Noonan
150Florida Institute of Technology, Melbourne, USA
150,
M Rahmani
M Rahmani
150Florida Institute of Technology, Melbourne, USA
150,
T Roy
T Roy
150Florida Institute of Technology, Melbourne, USA
150,
F Yumiceva
F Yumiceva
150Florida Institute of Technology, Melbourne, USA
150,
M R Adams
M R Adams
151University of Illinois at Chicago (UIC), Chicago, USA
151,
L Apanasevich
L Apanasevich
151University of Illinois at Chicago (UIC), Chicago, USA
151,
D Berry
D Berry
151University of Illinois at Chicago (UIC), Chicago, USA
151,
R R Betts
R R Betts
151University of Illinois at Chicago (UIC), Chicago, USA
151,
R Cavanaugh
R Cavanaugh
151University of Illinois at Chicago (UIC), Chicago, USA
151,
X Chen
X Chen
151University of Illinois at Chicago (UIC), Chicago, USA
151,
S Dittmer
S Dittmer
151University of Illinois at Chicago (UIC), Chicago, USA
151,
O Evdokimov
O Evdokimov
151University of Illinois at Chicago (UIC), Chicago, USA
151,
C E Gerber
C E Gerber
151University of Illinois at Chicago (UIC), Chicago, USA
151,
D A Hangal
D A Hangal
151University of Illinois at Chicago (UIC), Chicago, USA
151,
D J Hofman
D J Hofman
151University of Illinois at Chicago (UIC), Chicago, USA
151,
K Jung
K Jung
151University of Illinois at Chicago (UIC), Chicago, USA
151,
J Kamin
J Kamin
151University of Illinois at Chicago (UIC), Chicago, USA
151,
C Mills
C Mills
151University of Illinois at Chicago (UIC), Chicago, USA
151,
I D Sandoval Gonzalez
I D Sandoval Gonzalez
151University of Illinois at Chicago (UIC), Chicago, USA
151,
M B Tonjes
M B Tonjes
151University of Illinois at Chicago (UIC), Chicago, USA
151,
N Varelas
N Varelas
151University of Illinois at Chicago (UIC), Chicago, USA
151,
H Wang
H Wang
151University of Illinois at Chicago (UIC), Chicago, USA
151,
X Wang
X Wang
151University of Illinois at Chicago (UIC), Chicago, USA
151,
Z Wu
Z Wu
151University of Illinois at Chicago (UIC), Chicago, USA
151,
J Zhang
J Zhang
151University of Illinois at Chicago (UIC), Chicago, USA
151,
M Alhusseini
M Alhusseini
152The University of Iowa, Iowa City, USA
152,
B Bilki
B Bilki
152The University of Iowa, Iowa City, USA
152,
W Clarida
W Clarida
152The University of Iowa, Iowa City, USA
152,
K Dilsiz
K Dilsiz
152The University of Iowa, Iowa City, USA
152,
S Durgut
S Durgut
152The University of Iowa, Iowa City, USA
152,
R P Gandrajula
R P Gandrajula
152The University of Iowa, Iowa City, USA
152,
M Haytmyradov
M Haytmyradov
152The University of Iowa, Iowa City, USA
152,
V Khristenko
V Khristenko
152The University of Iowa, Iowa City, USA
152,
J-P Merlo
J-P Merlo
152The University of Iowa, Iowa City, USA
152,
A Mestvirishvili
A Mestvirishvili
152The University of Iowa, Iowa City, USA
152,
A Moeller
A Moeller
152The University of Iowa, Iowa City, USA
152,
J Nachtman
J Nachtman
152The University of Iowa, Iowa City, USA
152,
H Ogul
H Ogul
152The University of Iowa, Iowa City, USA
152,
Y Onel
Y Onel
152The University of Iowa, Iowa City, USA
152,
F Ozok
F Ozok
152The University of Iowa, Iowa City, USA
152,
A Penzo
A Penzo
152The University of Iowa, Iowa City, USA
152,
C Snyder
C Snyder
152The University of Iowa, Iowa City, USA
152,
E Tiras
E Tiras
152The University of Iowa, Iowa City, USA
152,
J Wetzel
J Wetzel
152The University of Iowa, Iowa City, USA
152,
B Blumenfeld
B Blumenfeld
153Johns Hopkins University, Baltimore, USA
153,
A Cocoros
A Cocoros
153Johns Hopkins University, Baltimore, USA
153,
N Eminizer
N Eminizer
153Johns Hopkins University, Baltimore, USA
153,
D Fehling
D Fehling
153Johns Hopkins University, Baltimore, USA
153,
L Feng
L Feng
153Johns Hopkins University, Baltimore, USA
153,
A V Gritsan
A V Gritsan
153Johns Hopkins University, Baltimore, USA
153,
W T Hung
W T Hung
153Johns Hopkins University, Baltimore, USA
153,
P Maksimovic
P Maksimovic
153Johns Hopkins University, Baltimore, USA
153,
J Roskes
J Roskes
153Johns Hopkins University, Baltimore, USA
153,
U Sarica
U Sarica
153Johns Hopkins University, Baltimore, USA
153,
M Swartz
M Swartz
153Johns Hopkins University, Baltimore, USA
153,
M Xiao
M Xiao
153Johns Hopkins University, Baltimore, USA
153,
C You
C You
153Johns Hopkins University, Baltimore, USA
153,
A Al-bataineh
A Al-bataineh
154The University of Kansas, Lawrence, USA
154,
P Baringer
P Baringer
154The University of Kansas, Lawrence, USA
154,
A Bean
A Bean
154The University of Kansas, Lawrence, USA
154,
S Boren
S Boren
154The University of Kansas, Lawrence, USA
154,
J Bowen
J Bowen
154The University of Kansas, Lawrence, USA
154,
A Bylinkin
A Bylinkin
154The University of Kansas, Lawrence, USA
154,
J Castle
J Castle
154The University of Kansas, Lawrence, USA
154,
S Khalil
S Khalil
154The University of Kansas, Lawrence, USA
154,
A Kropivnitskaya
A Kropivnitskaya
154The University of Kansas, Lawrence, USA
154,
D Majumder
D Majumder
154The University of Kansas, Lawrence, USA
154,
W Mcbrayer
W Mcbrayer
154The University of Kansas, Lawrence, USA
154,
M Murray
M Murray
154The University of Kansas, Lawrence, USA
154,
C Rogan
C Rogan
154The University of Kansas, Lawrence, USA
154,
S Sanders
S Sanders
154The University of Kansas, Lawrence, USA
154,
E Schmitz
E Schmitz
154The University of Kansas, Lawrence, USA
154,
J D Tapia Takaki
J D Tapia Takaki
154The University of Kansas, Lawrence, USA
154,
Q Wang
Q Wang
154The University of Kansas, Lawrence, USA
154,
A Ivanov
A Ivanov
155Kansas State University, Manhattan, USA
155,
K Kaadze
K Kaadze
155Kansas State University, Manhattan, USA
155,
D Kim
D Kim
155Kansas State University, Manhattan, USA
155,
Y Maravin
Y Maravin
155Kansas State University, Manhattan, USA
155,
D R Mendis
D R Mendis
155Kansas State University, Manhattan, USA
155,
T Mitchell
T Mitchell
155Kansas State University, Manhattan, USA
155,
A Modak
A Modak
155Kansas State University, Manhattan, USA
155,
A Mohammadi
A Mohammadi
155Kansas State University, Manhattan, USA
155,
L K Saini
L K Saini
155Kansas State University, Manhattan, USA
155,
N Skhirtladze
N Skhirtladze
155Kansas State University, Manhattan, USA
155,
F Rebassoo
F Rebassoo
156Lawrence Livermore National Laboratory, Livermore, USA
156,
D Wright
D Wright
156Lawrence Livermore National Laboratory, Livermore, USA
156,
A Baden
A Baden
157University of Maryland, College Park, USA
157,
O Baron
O Baron
157University of Maryland, College Park, USA
157,
A Belloni
A Belloni
157University of Maryland, College Park, USA
157,
S C Eno
S C Eno
157University of Maryland, College Park, USA
157,
Y Feng
Y Feng
157University of Maryland, College Park, USA
157,
C Ferraioli
C Ferraioli
157University of Maryland, College Park, USA
157,
N J Hadley
N J Hadley
157University of Maryland, College Park, USA
157,
S Jabeen
S Jabeen
157University of Maryland, College Park, USA
157,
G Y Jeng
G Y Jeng
157University of Maryland, College Park, USA
157,
R G Kellogg
R G Kellogg
157University of Maryland, College Park, USA
157,
J Kunkle
J Kunkle
157University of Maryland, College Park, USA
157,
A C Mignerey
A C Mignerey
157University of Maryland, College Park, USA
157,
F Ricci-Tam
F Ricci-Tam
157University of Maryland, College Park, USA
157,
Y H Shin
Y H Shin
157University of Maryland, College Park, USA
157,
A Skuja
A Skuja
157University of Maryland, College Park, USA
157,
S C Tonwar
S C Tonwar
157University of Maryland, College Park, USA
157,
K Wong
K Wong
157University of Maryland, College Park, USA
157,
D Abercrombie
D Abercrombie
158Massachusetts Institute of Technology, Cambridge, USA
158,
B Allen
B Allen
158Massachusetts Institute of Technology, Cambridge, USA
158,
V Azzolini
V Azzolini
158Massachusetts Institute of Technology, Cambridge, USA
158,
A Baty
A Baty
158Massachusetts Institute of Technology, Cambridge, USA
158,
G Bauer
G Bauer
158Massachusetts Institute of Technology, Cambridge, USA
158,
R Bi
R Bi
158Massachusetts Institute of Technology, Cambridge, USA
158,
S Brandt
S Brandt
158Massachusetts Institute of Technology, Cambridge, USA
158,
W Busza
W Busza
158Massachusetts Institute of Technology, Cambridge, USA
158,
I A Cali
I A Cali
158Massachusetts Institute of Technology, Cambridge, USA
158,
M D’Alfonso
M D’Alfonso
158Massachusetts Institute of Technology, Cambridge, USA
158,
Z Demiragli
Z Demiragli
158Massachusetts Institute of Technology, Cambridge, USA
158,
G Gomez Ceballos
G Gomez Ceballos
158Massachusetts Institute of Technology, Cambridge, USA
158,
M Goncharov
M Goncharov
158Massachusetts Institute of Technology, Cambridge, USA
158,
P Harris
P Harris
158Massachusetts Institute of Technology, Cambridge, USA
158,
D Hsu
D Hsu
158Massachusetts Institute of Technology, Cambridge, USA
158,
M Hu
M Hu
158Massachusetts Institute of Technology, Cambridge, USA
158,
Y Iiyama
Y Iiyama
158Massachusetts Institute of Technology, Cambridge, USA
158,
G M Innocenti
G M Innocenti
158Massachusetts Institute of Technology, Cambridge, USA
158,
M Klute
M Klute
158Massachusetts Institute of Technology, Cambridge, USA
158,
D Kovalskyi
D Kovalskyi
158Massachusetts Institute of Technology, Cambridge, USA
158,
Y-J Lee
Y-J Lee
158Massachusetts Institute of Technology, Cambridge, USA
158,
P D Luckey
P D Luckey
158Massachusetts Institute of Technology, Cambridge, USA
158,
B Maier
B Maier
158Massachusetts Institute of Technology, Cambridge, USA
158,
A C Marini
A C Marini
158Massachusetts Institute of Technology, Cambridge, USA
158,
C Mcginn
C Mcginn
158Massachusetts Institute of Technology, Cambridge, USA
158,
C Mironov
C Mironov
158Massachusetts Institute of Technology, Cambridge, USA
158,
S Narayanan
S Narayanan
158Massachusetts Institute of Technology, Cambridge, USA
158,
X Niu
X Niu
158Massachusetts Institute of Technology, Cambridge, USA
158,
C Paus
C Paus
158Massachusetts Institute of Technology, Cambridge, USA
158,
C Roland
C Roland
158Massachusetts Institute of Technology, Cambridge, USA
158,
G Roland
G Roland
158Massachusetts Institute of Technology, Cambridge, USA
158,
G S F Stephans
G S F Stephans
158Massachusetts Institute of Technology, Cambridge, USA
158,
K Sumorok
K Sumorok
158Massachusetts Institute of Technology, Cambridge, USA
158,
K Tatar
K Tatar
158Massachusetts Institute of Technology, Cambridge, USA
158,
D Velicanu
D Velicanu
158Massachusetts Institute of Technology, Cambridge, USA
158,
J Wang
J Wang
158Massachusetts Institute of Technology, Cambridge, USA
158,
T W Wang
T W Wang
158Massachusetts Institute of Technology, Cambridge, USA
158,
B Wyslouch
B Wyslouch
158Massachusetts Institute of Technology, Cambridge, USA
158,
S Zhaozhong
S Zhaozhong
158Massachusetts Institute of Technology, Cambridge, USA
158,
A C Benvenuti
A C Benvenuti
159University of Minnesota, Minneapolis, USA
159,
R M Chatterjee
R M Chatterjee
159University of Minnesota, Minneapolis, USA
159,
A Evans
A Evans
159University of Minnesota, Minneapolis, USA
159,
P Hansen
P Hansen
159University of Minnesota, Minneapolis, USA
159,
S Kalafut
S Kalafut
159University of Minnesota, Minneapolis, USA
159,
Y Kubota
Y Kubota
159University of Minnesota, Minneapolis, USA
159,
Z Lesko
Z Lesko
159University of Minnesota, Minneapolis, USA
159,
J Mans
J Mans
159University of Minnesota, Minneapolis, USA
159,
S Nourbakhsh
S Nourbakhsh
159University of Minnesota, Minneapolis, USA
159,
N Ruckstuhl
N Ruckstuhl
159University of Minnesota, Minneapolis, USA
159,
R Rusack
R Rusack
159University of Minnesota, Minneapolis, USA
159,
J Turkewitz
J Turkewitz
159University of Minnesota, Minneapolis, USA
159,
M A Wadud
M A Wadud
159University of Minnesota, Minneapolis, USA
159,
J G Acosta
J G Acosta
160University of Mississippi, Oxford, USA
160,
S Oliveros
S Oliveros
160University of Mississippi, Oxford, USA
160,
E Avdeeva
E Avdeeva
161University of Nebraska-Lincoln, Lincoln, USA
161,
K Bloom
K Bloom
161University of Nebraska-Lincoln, Lincoln, USA
161,
D R Claes
D R Claes
161University of Nebraska-Lincoln, Lincoln, USA
161,
C Fangmeier
C Fangmeier
161University of Nebraska-Lincoln, Lincoln, USA
161,
F Golf
F Golf
161University of Nebraska-Lincoln, Lincoln, USA
161,
R Gonzalez Suarez
R Gonzalez Suarez
161University of Nebraska-Lincoln, Lincoln, USA
161,
R Kamalieddin
R Kamalieddin
161University of Nebraska-Lincoln, Lincoln, USA
161,
I Kravchenko
I Kravchenko
161University of Nebraska-Lincoln, Lincoln, USA
161,
J Monroy
J Monroy
161University of Nebraska-Lincoln, Lincoln, USA
161,
J E Siado
J E Siado
161University of Nebraska-Lincoln, Lincoln, USA
161,
G R Snow
G R Snow
161University of Nebraska-Lincoln, Lincoln, USA
161,
B Stieger
B Stieger
161University of Nebraska-Lincoln, Lincoln, USA
161,
A Godshalk
A Godshalk
162State University of New York at Buffalo, Buffalo, USA
162,
C Harrington
C Harrington
162State University of New York at Buffalo, Buffalo, USA
162,
I Iashvili
I Iashvili
162State University of New York at Buffalo, Buffalo, USA
162,
A Kharchilava
A Kharchilava
162State University of New York at Buffalo, Buffalo, USA
162,
D Nguyen
D Nguyen
162State University of New York at Buffalo, Buffalo, USA
162,
A Parker
A Parker
162State University of New York at Buffalo, Buffalo, USA
162,
S Rappoccio
S Rappoccio
162State University of New York at Buffalo, Buffalo, USA
162,
B Roozbahani
B Roozbahani
162State University of New York at Buffalo, Buffalo, USA
162,
E Barberis
E Barberis
163Northeastern University, Boston, USA
163,
C Freer
C Freer
163Northeastern University, Boston, USA
163,
A Hortiangtham
A Hortiangtham
163Northeastern University, Boston, USA
163,
D M Morse
D M Morse
163Northeastern University, Boston, USA
163,
T Orimoto
T Orimoto
163Northeastern University, Boston, USA
163,
R Teixeira De Lima
R Teixeira De Lima
163Northeastern University, Boston, USA
163,
T Wamorkar
T Wamorkar
163Northeastern University, Boston, USA
163,
B Wang
B Wang
163Northeastern University, Boston, USA
163,
A Wisecarver
A Wisecarver
163Northeastern University, Boston, USA
163,
D Wood
D Wood
163Northeastern University, Boston, USA
163,
S Bhattacharya
S Bhattacharya
164Northwestern University, Evanston, USA
164,
O Charaf
O Charaf
164Northwestern University, Evanston, USA
164,
K A Hahn
K A Hahn
164Northwestern University, Evanston, USA
164,
N Mucia
N Mucia
164Northwestern University, Evanston, USA
164,
N Odell
N Odell
164Northwestern University, Evanston, USA
164,
M H Schmitt
M H Schmitt
164Northwestern University, Evanston, USA
164,
K Sung
K Sung
164Northwestern University, Evanston, USA
164,
M Trovato
M Trovato
164Northwestern University, Evanston, USA
164,
M Velasco
M Velasco
164Northwestern University, Evanston, USA
164,
R Bucci
R Bucci
165University of Notre Dame, Notre Dame, USA
165,
N Dev
N Dev
165University of Notre Dame, Notre Dame, USA
165,
M Hildreth
M Hildreth
165University of Notre Dame, Notre Dame, USA
165,
K Hurtado Anampa
K Hurtado Anampa
165University of Notre Dame, Notre Dame, USA
165,
C Jessop
C Jessop
165University of Notre Dame, Notre Dame, USA
165,
D J Karmgard
D J Karmgard
165University of Notre Dame, Notre Dame, USA
165,
N Kellams
N Kellams
165University of Notre Dame, Notre Dame, USA
165,
K Lannon
K Lannon
165University of Notre Dame, Notre Dame, USA
165,
W Li
W Li
165University of Notre Dame, Notre Dame, USA
165,
N Loukas
N Loukas
165University of Notre Dame, Notre Dame, USA
165,
N Marinelli
N Marinelli
165University of Notre Dame, Notre Dame, USA
165,
F Meng
F Meng
165University of Notre Dame, Notre Dame, USA
165,
C Mueller
C Mueller
165University of Notre Dame, Notre Dame, USA
165,
Y Musienko
Y Musienko
165University of Notre Dame, Notre Dame, USA
165,
M Planer
M Planer
165University of Notre Dame, Notre Dame, USA
165,
A Reinsvold
A Reinsvold
165University of Notre Dame, Notre Dame, USA
165,
R Ruchti
R Ruchti
165University of Notre Dame, Notre Dame, USA
165,
P Siddireddy
P Siddireddy
165University of Notre Dame, Notre Dame, USA
165,
G Smith
G Smith
165University of Notre Dame, Notre Dame, USA
165,
S Taroni
S Taroni
165University of Notre Dame, Notre Dame, USA
165,
M Wayne
M Wayne
165University of Notre Dame, Notre Dame, USA
165,
A Wightman
A Wightman
165University of Notre Dame, Notre Dame, USA
165,
M Wolf
M Wolf
165University of Notre Dame, Notre Dame, USA
165,
A Woodard
A Woodard
165University of Notre Dame, Notre Dame, USA
165,
J Alimena
J Alimena
166The Ohio State University, Columbus, USA
166,
L Antonelli
L Antonelli
166The Ohio State University, Columbus, USA
166,
B Bylsma
B Bylsma
166The Ohio State University, Columbus, USA
166,
L S Durkin
L S Durkin
166The Ohio State University, Columbus, USA
166,
S Flowers
S Flowers
166The Ohio State University, Columbus, USA
166,
B Francis
B Francis
166The Ohio State University, Columbus, USA
166,
A Hart
A Hart
166The Ohio State University, Columbus, USA
166,
C Hill
C Hill
166The Ohio State University, Columbus, USA
166,
W Ji
W Ji
166The Ohio State University, Columbus, USA
166,
T Y Ling
T Y Ling
166The Ohio State University, Columbus, USA
166,
W Luo
W Luo
166The Ohio State University, Columbus, USA
166,
B L Winer
B L Winer
166The Ohio State University, Columbus, USA
166,
H W Wulsin
H W Wulsin
166The Ohio State University, Columbus, USA
166,
S Cooperstein
S Cooperstein
167Princeton University, Princeton, USA
167,
P Elmer
P Elmer
167Princeton University, Princeton, USA
167,
J Hardenbrook
J Hardenbrook
167Princeton University, Princeton, USA
167,
P Hebda
P Hebda
167Princeton University, Princeton, USA
167,
S Higginbotham
S Higginbotham
167Princeton University, Princeton, USA
167,
A Kalogeropoulos
A Kalogeropoulos
167Princeton University, Princeton, USA
167,
D Lange
D Lange
167Princeton University, Princeton, USA
167,
M T Lucchini
M T Lucchini
167Princeton University, Princeton, USA
167,
J Luo
J Luo
167Princeton University, Princeton, USA
167,
D Marlow
D Marlow
167Princeton University, Princeton, USA
167,
K Mei
K Mei
167Princeton University, Princeton, USA
167,
I Ojalvo
I Ojalvo
167Princeton University, Princeton, USA
167,
J Olsen
J Olsen
167Princeton University, Princeton, USA
167,
C Palmer
C Palmer
167Princeton University, Princeton, USA
167,
P Piroué
P Piroué
167Princeton University, Princeton, USA
167,
J Salfeld-Nebgen
J Salfeld-Nebgen
167Princeton University, Princeton, USA
167,
D Stickland
D Stickland
167Princeton University, Princeton, USA
167,
C Tully
C Tully
167Princeton University, Princeton, USA
167,
S Malik
S Malik
168University of Puerto Rico, Mayagüez, USA
168,
S Norberg
S Norberg
168University of Puerto Rico, Mayagüez, USA
168,
A Barker
A Barker
169Purdue University, West Lafayette, USA
169,
V E Barnes
V E Barnes
169Purdue University, West Lafayette, USA
169,
L Gutay
L Gutay
169Purdue University, West Lafayette, USA
169,
M Jones
M Jones
169Purdue University, West Lafayette, USA
169,
A W Jung
A W Jung
169Purdue University, West Lafayette, USA
169,
A Khatiwada
A Khatiwada
169Purdue University, West Lafayette, USA
169,
B Mahakud
B Mahakud
169Purdue University, West Lafayette, USA
169,
D H Miller
D H Miller
169Purdue University, West Lafayette, USA
169,
N Neumeister
N Neumeister
169Purdue University, West Lafayette, USA
169,
C C Peng
C C Peng
169Purdue University, West Lafayette, USA
169,
H Qiu
H Qiu
169Purdue University, West Lafayette, USA
169,
J F Schulte
J F Schulte
169Purdue University, West Lafayette, USA
169,
J Sun
J Sun
169Purdue University, West Lafayette, USA
169,
F Wang
F Wang
169Purdue University, West Lafayette, USA
169,
R Xiao
R Xiao
169Purdue University, West Lafayette, USA
169,
W Xie
W Xie
169Purdue University, West Lafayette, USA
169,
T Cheng
T Cheng
170Purdue University Northwest, Hammond, USA
170,
J Dolen
J Dolen
170Purdue University Northwest, Hammond, USA
170,
N Parashar
N Parashar
170Purdue University Northwest, Hammond, USA
170,
Z Chen
Z Chen
171Rice University, Houston, USA
171,
K M Ecklund
K M Ecklund
171Rice University, Houston, USA
171,
S Freed
S Freed
171Rice University, Houston, USA
171,
F J M Geurts
F J M Geurts
171Rice University, Houston, USA
171,
M Kilpatrick
M Kilpatrick
171Rice University, Houston, USA
171,
W Li
W Li
171Rice University, Houston, USA
171,
B Michlin
B Michlin
171Rice University, Houston, USA
171,
B P Padley
B P Padley
171Rice University, Houston, USA
171,
J Roberts
J Roberts
171Rice University, Houston, USA
171,
J Rorie
J Rorie
171Rice University, Houston, USA
171,
W Shi
W Shi
171Rice University, Houston, USA
171,
Z Tu
Z Tu
171Rice University, Houston, USA
171,
J Zabel
J Zabel
171Rice University, Houston, USA
171,
A Zhang
A Zhang
171Rice University, Houston, USA
171,
A Bodek
A Bodek
172University of Rochester, Rochester, USA
172,
P de Barbaro
P de Barbaro
172University of Rochester, Rochester, USA
172,
R Demina
R Demina
172University of Rochester, Rochester, USA
172,
Y t Duh
Y t Duh
172University of Rochester, Rochester, USA
172,
J L Dulemba
J L Dulemba
172University of Rochester, Rochester, USA
172,
C Fallon
C Fallon
172University of Rochester, Rochester, USA
172,
T Ferbel
T Ferbel
172University of Rochester, Rochester, USA
172,
M Galanti
M Galanti
172University of Rochester, Rochester, USA
172,
A Garcia-Bellido
A Garcia-Bellido
172University of Rochester, Rochester, USA
172,
J Han
J Han
172University of Rochester, Rochester, USA
172,
O Hindrichs
O Hindrichs
172University of Rochester, Rochester, USA
172,
A Khukhunaishvili
A Khukhunaishvili
172University of Rochester, Rochester, USA
172,
K H Lo
K H Lo
172University of Rochester, Rochester, USA
172,
P Tan
P Tan
172University of Rochester, Rochester, USA
172,
R Taus
R Taus
172University of Rochester, Rochester, USA
172,
M Verzetti
M Verzetti
172University of Rochester, Rochester, USA
172,
A Agapitos
A Agapitos
173Rutgers, The State University of New Jersey, Piscataway, USA
173,
J P Chou
J P Chou
173Rutgers, The State University of New Jersey, Piscataway, USA
173,
Y Gershtein
Y Gershtein
173Rutgers, The State University of New Jersey, Piscataway, USA
173,
T A Gómez Espinosa
T A Gómez Espinosa
173Rutgers, The State University of New Jersey, Piscataway, USA
173,
E Halkiadakis
E Halkiadakis
173Rutgers, The State University of New Jersey, Piscataway, USA
173,
M Heindl
M Heindl
173Rutgers, The State University of New Jersey, Piscataway, USA
173,
E Hughes
E Hughes
173Rutgers, The State University of New Jersey, Piscataway, USA
173,
S Kaplan
S Kaplan
173Rutgers, The State University of New Jersey, Piscataway, USA
173,
R Kunnawalkam Elayavalli
R Kunnawalkam Elayavalli
173Rutgers, The State University of New Jersey, Piscataway, USA
173,
S Kyriacou
S Kyriacou
173Rutgers, The State University of New Jersey, Piscataway, USA
173,
A Lath
A Lath
173Rutgers, The State University of New Jersey, Piscataway, USA
173,
R Montalvo
R Montalvo
173Rutgers, The State University of New Jersey, Piscataway, USA
173,
K Nash
K Nash
173Rutgers, The State University of New Jersey, Piscataway, USA
173,
M Osherson
M Osherson
173Rutgers, The State University of New Jersey, Piscataway, USA
173,
H Saka
H Saka
173Rutgers, The State University of New Jersey, Piscataway, USA
173,
S Salur
S Salur
173Rutgers, The State University of New Jersey, Piscataway, USA
173,
S Schnetzer
S Schnetzer
173Rutgers, The State University of New Jersey, Piscataway, USA
173,
D Sheffield
D Sheffield
173Rutgers, The State University of New Jersey, Piscataway, USA
173,
S Somalwar
S Somalwar
173Rutgers, The State University of New Jersey, Piscataway, USA
173,
R Stone
R Stone
173Rutgers, The State University of New Jersey, Piscataway, USA
173,
S Thomas
S Thomas
173Rutgers, The State University of New Jersey, Piscataway, USA
173,
P Thomassen
P Thomassen
173Rutgers, The State University of New Jersey, Piscataway, USA
173,
M Walker
M Walker
173Rutgers, The State University of New Jersey, Piscataway, USA
173,
A G Delannoy
A G Delannoy
174University of Tennessee, Knoxville, USA
174,
J Heideman
J Heideman
174University of Tennessee, Knoxville, USA
174,
G Riley
G Riley
174University of Tennessee, Knoxville, USA
174,
K Rose
K Rose
174University of Tennessee, Knoxville, USA
174,
S Spanier
S Spanier
174University of Tennessee, Knoxville, USA
174,
K Thapa
K Thapa
174University of Tennessee, Knoxville, USA
174,
O Bouhali
O Bouhali
175Texas A&M University, College Station, USA
175,
A Castaneda Hernandez
A Castaneda Hernandez
175Texas A&M University, College Station, USA
175,
A Celik
A Celik
175Texas A&M University, College Station, USA
175,
M Dalchenko
M Dalchenko
175Texas A&M University, College Station, USA
175,
M De Mattia
M De Mattia
175Texas A&M University, College Station, USA
175,
A Delgado
A Delgado
175Texas A&M University, College Station, USA
175,
S Dildick
S Dildick
175Texas A&M University, College Station, USA
175,
R Eusebi
R Eusebi
175Texas A&M University, College Station, USA
175,
J Gilmore
J Gilmore
175Texas A&M University, College Station, USA
175,
T Huang
T Huang
175Texas A&M University, College Station, USA
175,
T Kamon
T Kamon
175Texas A&M University, College Station, USA
175,
S Luo
S Luo
175Texas A&M University, College Station, USA
175,
R Mueller
R Mueller
175Texas A&M University, College Station, USA
175,
Y Pakhotin
Y Pakhotin
175Texas A&M University, College Station, USA
175,
R Patel
R Patel
175Texas A&M University, College Station, USA
175,
A Perloff
A Perloff
175Texas A&M University, College Station, USA
175,
L Perniè
L Perniè
175Texas A&M University, College Station, USA
175,
D Rathjens
D Rathjens
175Texas A&M University, College Station, USA
175,
A Safonov
A Safonov
175Texas A&M University, College Station, USA
175,
A Tatarinov
A Tatarinov
175Texas A&M University, College Station, USA
175,
N Akchurin
N Akchurin
176Texas Tech University, Lubbock, USA
176,
J Damgov
J Damgov
176Texas Tech University, Lubbock, USA
176,
F De Guio
F De Guio
176Texas Tech University, Lubbock, USA
176,
P R Dudero
P R Dudero
176Texas Tech University, Lubbock, USA
176,
S Kunori
S Kunori
176Texas Tech University, Lubbock, USA
176,
K Lamichhane
K Lamichhane
176Texas Tech University, Lubbock, USA
176,
S W Lee
S W Lee
176Texas Tech University, Lubbock, USA
176,
T Mengke
T Mengke
176Texas Tech University, Lubbock, USA
176,
S Muthumuni
S Muthumuni
176Texas Tech University, Lubbock, USA
176,
T Peltola
T Peltola
176Texas Tech University, Lubbock, USA
176,
S Undleeb
S Undleeb
176Texas Tech University, Lubbock, USA
176,
I Volobouev
I Volobouev
176Texas Tech University, Lubbock, USA
176,
Z Wang
Z Wang
176Texas Tech University, Lubbock, USA
176,
S Greene
S Greene
177Vanderbilt University, Nashville, USA
177,
A Gurrola
A Gurrola
177Vanderbilt University, Nashville, USA
177,
R Janjam
R Janjam
177Vanderbilt University, Nashville, USA
177,
W Johns
W Johns
177Vanderbilt University, Nashville, USA
177,
C Maguire
C Maguire
177Vanderbilt University, Nashville, USA
177,
A Melo
A Melo
177Vanderbilt University, Nashville, USA
177,
H Ni
H Ni
177Vanderbilt University, Nashville, USA
177,
K Padeken
K Padeken
177Vanderbilt University, Nashville, USA
177,
J D Ruiz Alvarez
J D Ruiz Alvarez
177Vanderbilt University, Nashville, USA
177,
P Sheldon
P Sheldon
177Vanderbilt University, Nashville, USA
177,
S Tuo
S Tuo
177Vanderbilt University, Nashville, USA
177,
J Velkovska
J Velkovska
177Vanderbilt University, Nashville, USA
177,
M Verweij
M Verweij
177Vanderbilt University, Nashville, USA
177,
Q Xu
Q Xu
177Vanderbilt University, Nashville, USA
177,
M W Arenton
M W Arenton
178University of Virginia, Charlottesville, USA
178,
P Barria
P Barria
178University of Virginia, Charlottesville, USA
178,
B Cox
B Cox
178University of Virginia, Charlottesville, USA
178,
R Hirosky
R Hirosky
178University of Virginia, Charlottesville, USA
178,
M Joyce
M Joyce
178University of Virginia, Charlottesville, USA
178,
A Ledovskoy
A Ledovskoy
178University of Virginia, Charlottesville, USA
178,
H Li
H Li
178University of Virginia, Charlottesville, USA
178,
C Neu
C Neu
178University of Virginia, Charlottesville, USA
178,
T Sinthuprasith
T Sinthuprasith
178University of Virginia, Charlottesville, USA
178,
Y Wang
Y Wang
178University of Virginia, Charlottesville, USA
178,
E Wolfe
E Wolfe
178University of Virginia, Charlottesville, USA
178,
F Xia
F Xia
178University of Virginia, Charlottesville, USA
178,
R Harr
R Harr
179Wayne State University, Detroit, USA
179,
P E Karchin
P E Karchin
179Wayne State University, Detroit, USA
179,
N Poudyal
N Poudyal
179Wayne State University, Detroit, USA
179,
J Sturdy
J Sturdy
179Wayne State University, Detroit, USA
179,
P Thapa
P Thapa
179Wayne State University, Detroit, USA
179,
S Zaleski
S Zaleski
179Wayne State University, Detroit, USA
179,
M Brodski
M Brodski
180University of Wisconsin-Madison, Madison, WI USA
180,
J Buchanan
J Buchanan
180University of Wisconsin-Madison, Madison, WI USA
180,
C Caillol
C Caillol
180University of Wisconsin-Madison, Madison, WI USA
180,
D Carlsmith
D Carlsmith
180University of Wisconsin-Madison, Madison, WI USA
180,
S Dasu
S Dasu
180University of Wisconsin-Madison, Madison, WI USA
180,
L Dodd
L Dodd
180University of Wisconsin-Madison, Madison, WI USA
180,
S Duric
S Duric
180University of Wisconsin-Madison, Madison, WI USA
180,
B Gomber
B Gomber
180University of Wisconsin-Madison, Madison, WI USA
180,
M Grothe
M Grothe
180University of Wisconsin-Madison, Madison, WI USA
180,
M Herndon
M Herndon
180University of Wisconsin-Madison, Madison, WI USA
180,
A Hervé
A Hervé
180University of Wisconsin-Madison, Madison, WI USA
180,
U Hussain
U Hussain
180University of Wisconsin-Madison, Madison, WI USA
180,
P Klabbers
P Klabbers
180University of Wisconsin-Madison, Madison, WI USA
180,
A Lanaro
A Lanaro
180University of Wisconsin-Madison, Madison, WI USA
180,
A Levine
A Levine
180University of Wisconsin-Madison, Madison, WI USA
180,
K Long
K Long
180University of Wisconsin-Madison, Madison, WI USA
180,
R Loveless
R Loveless
180University of Wisconsin-Madison, Madison, WI USA
180,
T Ruggles
T Ruggles
180University of Wisconsin-Madison, Madison, WI USA
180,
A Savin
A Savin
180University of Wisconsin-Madison, Madison, WI USA
180,
N Smith
N Smith
180University of Wisconsin-Madison, Madison, WI USA
180,
W H Smith
W H Smith
180University of Wisconsin-Madison, Madison, WI USA
180,
N Woods
N Woods
180University of Wisconsin-Madison, Madison, WI USA
180;
CMS Collaboration181