Fig. 1.

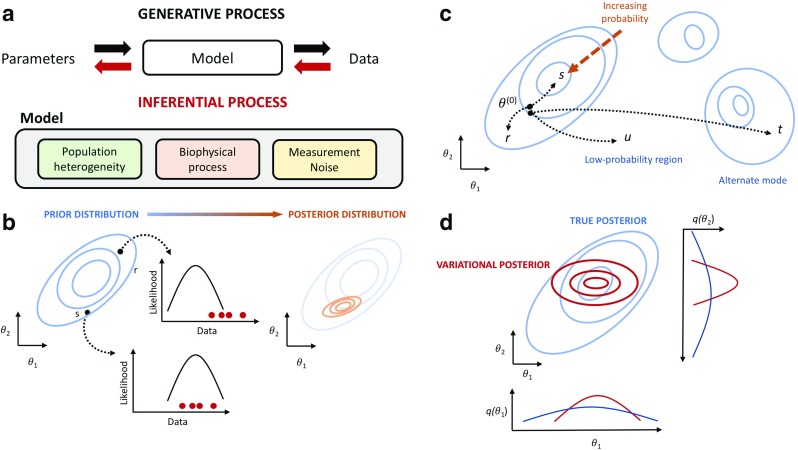
a Overview of Bayesian modelling. Data is assumed to be generated by a stochastic model which describes various underlying processes and is specified by some unknown parameters. Bayesian inference seeks to recover those parameters from the observed data. b Prior beliefs are expressed as a probability distribution over parameters 𝜃 = (𝜃₁,𝜃₂) which are updated when data is collected via the likelihood function to give a posterior distribution over 𝜃. c Real-world posterior distributions often contain a number of separated high probability regions. An ideal Metropolis-Hastings algorithm would possess a proposal mechanism that allows regular movement between different high-probability regions without the need to tranverse through low-probability intermediate regions. d Variational methods build approximations of the true posterior distribution. In this example, a mean-field approximation breaks the dependencies between the parameters (𝜃₁,𝜃₂) so the variational posterior models each dimension separately