Fig 3.

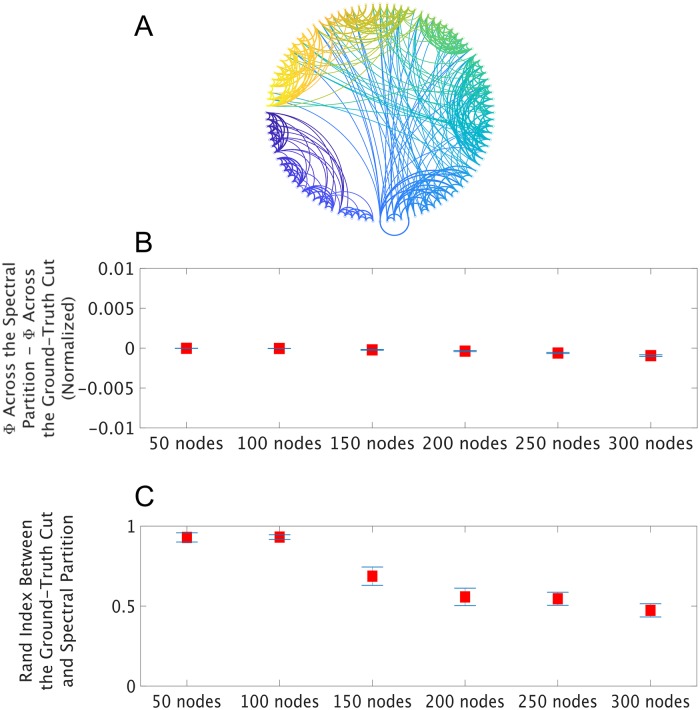
A Having shown that spectral clustering can find the MIB in time-series data from small networks, we next asked whether it could find the MIB of large simulated networks. While large networks cannot be exhaustively searched for their MIB, the MIB can be forced onto them by cutting them in half. We generated 40 such cut networks for each network size. Network sizes ranged from 50 nodes to 300 nodes. B Here, we show Φ^G (normalized) across the ground-truth cut subtracted from Φ^G (normalized) across the partition identified through spectral clustering. Red squares indicate the mean across 40 networks, the absolute value of which never exceeded 0.001 bits (normalized), and the blue bars indicate standard error of the mean. C Here, we show the mean and standard error of the Rand Index between the ground-truth cut and the spectral clustering-based partition of the correlation matrix estimated from each network. The Rand Index between the spectral partition and the ground-truth cut was greater than 0.8 (indicating high similarity) for the majority of networks of all network sizes, except for the 200- to 300-node networks. Despite this dip in Rand Index, spectral clustering still found partitions across which Φ^G (normalized) was extremely close to Φ^G (normalized) across the ground-truth cut in the 300-node networks (A), which suggests that in these networks, there was sometimes several possible partitions that minimized normalized integrated information. We found that spectral clustering performed even better (nearly perfectly) using the same networks but with autoregressive network dynamics (S8 Fig).