Skip to main content
. 2019 Jan 22;8(2):155–160. doi: 10.1021/acsmacrolett.8b00828

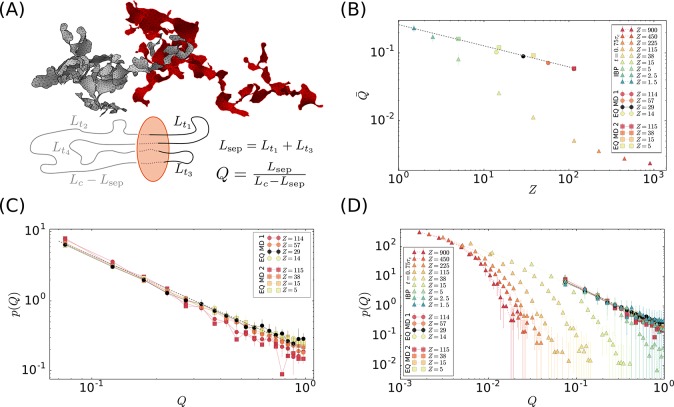
Figure 1.

Figure 1

Threading statistics in terms of relative contour length fraction Q. (A) Top: Minimal surfaces of a pair of close-by rings modeled as double-folded polymers on interacting branched primitive trees (IBP model). Bottom: Schematic representation of one ring (black and gray) penetrating the minimal surface of another ring (orange) of total contour length Lc. Lti is the contour length of subchain i penetrating the second ring. In this example, four surface penetrations (np = 4) split the penetrating ring into the segment pairs (Lt1,Lt3) and (Lt2,Lt4) which are on opposite sides of the surface: this defines the separation length, Lsep, and its complementary, Lc – Lsep. Adapted with permission from ref (33). (B) Mean relative contour length fraction, Q̅, of one ring threading another ring as a function of ring mass, Z. The dashed line is the best fit to the data for MD-equilibrated rings, Q̅ ≈ 0.26Z–0.31. (C) Probability distribution functions, p(Q) (log–log scale). Results for MD-equilibrated rings from polymer models EQ MD 1 and EQ MD 2. The dashed gray line p(Q) ∼ Q–1.35 is the best fit to the distributions tail. (D) Comparison between p(Q)’s for the IBP model and MD-equilibrated rings. In panels (C) and (D), the bin size is Qmax/20 with Qmax being the largest value of Q in the given data set.