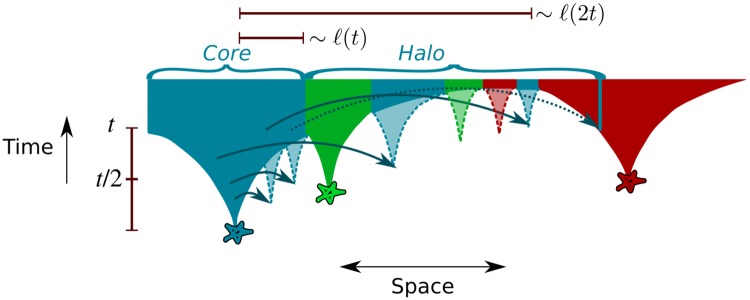
Fig 2. Marginal dynamics of jump-driven soft sweeps.

When long-range dispersal is significant, clones of different allelic identity (distinguished by colors) grow out of their originating mutations (stars) by accumulating satellite clusters (translucent cones). If only a single mutation were present, the extent ℓ(t) of the high-occupancy core (consisting of satellite clusters which have merged with the cluster growing out of the originating mutation) would, on average, follow a faster-than-linear growth rule, depicted schematically by the border of the opaque regions. For a wide range of kernels in the vicinity of μ = d, the growth rule arises from a hierarchy of length and time scales related by doublings in time: the satellite that merges with the core at time t would typically originate from a key jump out of the core at time t/2, that extended over a length of order ℓ(t) (solid arrows out of blue region). Looking forward in time, a clone whose core has grown for time t without being obstructed will have likely seeded satellites out to a distance of order ℓ(2t). In the presence of recurrent mutations, these satellites may be obstructed from merging with the core due to intervening cores and satellites of different mutational origin (green and red regions). For very broad dispersal kernels, the halo also includes rarer jumps out of the core (dashed arrow) that land in regions that are being taken over by other alleles, but establish themselves in stochastic gaps in those regions. The disconnected satellite clusters and isolated demes comprise the halo region of the mutant clone.