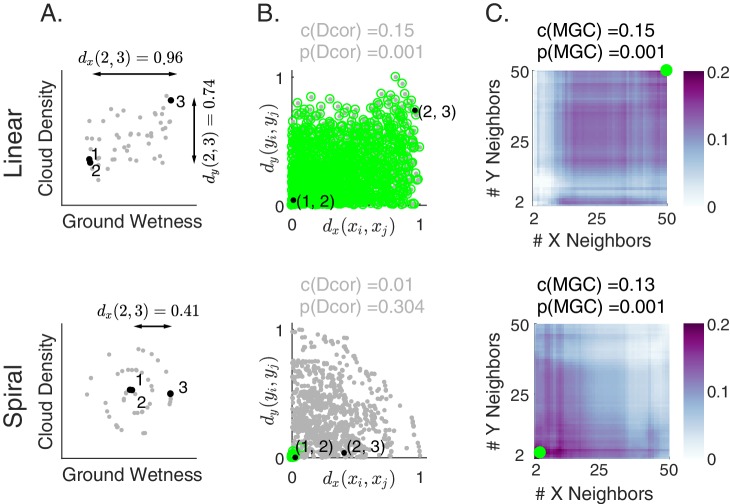
Figure 1. Illustration of Multiscale Graph Correlation (Mgc) on simulated cloud density ($x_i$) and grass wetness ($y_i$).

We present two different relationships: linear (top) and nonlinear spiral (bottom; see Materials and methods for simulation details). (A) Scatterplots of the raw data using $50$ pairs of samples for each scenario. Samples $1$, $2$, and $3$ (black) are highlighted; arrows show $x$ distances between these pairs of points while their $y$ distances are almost 0. (B) Scatterplots of all pairs of distances comparing $x$ and $y$ distances. Distances are linearly correlated in the linear relationship, whereas they are not in the spiral relationship. Dcorr uses all distances (gray dots) to compute its test statistic and p-value, whereas Mgc chooses the local scale and then uses only the local distances (green dots). (C) Heatmaps characterizing the strength of the generalized correlation at all possible scales (ranging from $2$ to $n$ for both $x$ and ${\displaystyle y}$). For the linear relationship, the global scale is optimal, which is the scale that Mgc selects and results in a p-value identical to Dcorr. For the nonlinear relationship, the optimal scale is local in both $x$ and $y$, so Mgc achieves a far larger test statistic, and a correspondingly smaller and significant p-value. Thus, Mgc uniquely detects dependence and characterizes the geometry in both relationships.