Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2019 Jan 25;19(2):1282–1288. doi: 10.1021/acs.nanolett.8b04862

High-Frequency Stochastic Switching of Graphene Resonators Near Room Temperature

Robin J Dolleman †, Pierpaolo Belardinelli ‡, Samer Houri †, Herre S J van der Zant †, Farbod Alijani ‡, Peter G Steeneken †,‡,*
PMCID: PMC6391039  PMID: 30681865

Abstract

graphic file with name nl-2018-04862y_0005.jpg

Stochastic switching between the two bistable states of a strongly driven mechanical resonator enables detection of weak signals based on probability distributions, in a manner that mimics biological systems. However, conventional silicon resonators at the microscale require a large amount of fluctuation power to achieve a switching rate in the order of a few hertz. Here, we employ graphene membrane resonators of atomic thickness to achieve a stochastic switching rate of 4.1 kHz, which is 100 times faster than current state-of-the-art. The (effective) temperature of the fluctuations is approximately 400 K, which is 3000 times lower than the state-of-the-art. This shows that these membranes are potentially useful to transduce weak signals in the audible frequency domain. Furthermore, we perform numerical simulations to understand the transition dynamics of the resonator and use analytical expressions to investigate the relevant scaling parameters that allow high-frequency, low-temperature stochastic switching to be achieved in mechanical resonators.

Keywords: Stochastic switching, NEMS, graphene, 2D materials, nonlinear dynamics

Stochastic switching is the process by which a system transitions randomly between two stable states, mediated by the fluctuations in the environment. This phenomenon has been observed in a variety of physical and biological systems.1−16 Similarly, mechanical resonators that are strongly driven can show stochastic switching between two stable attractors.17−19 This can potentially improve the transduction of small signals in a manner that mimics nature, by the stochastic resonance phenomenon.20−24 However, high fluctuation power, far above the fluctuations present at room temperature, needs to be applied to achieve stochastic switching. Despite the high resonance frequencies achieved by scaling down the resonators to the micro- or nanoscale regime, the switching rate is often quite low, on the order of 1 to 10 Hz. Extending this frequency range to the kilohertz regime, while lowering the fluctuation power, opens the door for new applications in the audible domain, such as ultrasensitive microphones.

Mechanical resonators consisting of an atomically thin membrane are ideal candidates to raise the switching rate. Their low mass ensures a megahertz resonance frequency that can be easily brought in the nonlinear regime. Graphene is a single layer of carbon atoms with excellent mechanical properties.25−27 Several works have demonstrated graphene resonators,28,29 showing nonlinear behavior30,31 and several practical applications such as pressure32−35 and gas sensors.36,37 The lower mass and low stiffness by virtue of the membrane’s thinness allows high switching rates to be achieved at lower fluctuation levels.24

Here we demonstrate high-frequency stochastic switching in strongly driven single-layer graphene drum resonators. Using an optical drive and readout, we bring the resonator into the bistable regime of the nonlinear Duffing response. By artificially adding random fluctuations to the drive, the effective temperature of the resonator is increased. We observe that the switching rate is increased with an effective temperature dependence that follows Kramer’s law.38 Switching rates as high as 4.1 kHz are observed close to room temperature. This work thus demonstrates a stochastic switching frequency that is more than a factor 100 higher than in prior works on mechanical resonators,24 at an effective temperature that is over a factor of 3000 lower. Having a high stochastic switching rate is important to enable high-bandwidth sensing using this sensitive technique. Moreover, a low effective temperature Teff is relevant to lower power consumption, and if Teff can be brought down to room temperature, the intrinsic Brownian motion of the resonator can be used to enable stochastic switching based sensors. With stochastic switching frequencies above 20 Hz, this work demonstrates the potential of graphene membranes to transduce signals in the audible frequency range.

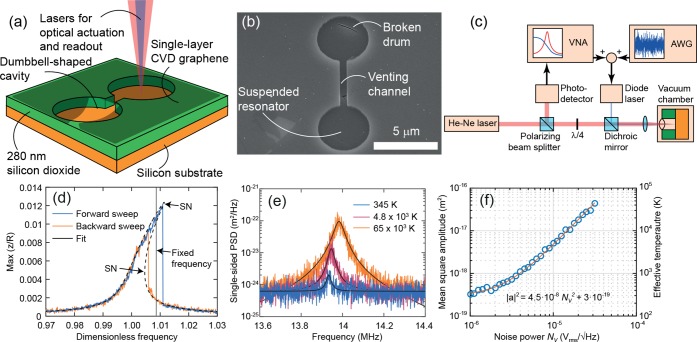
Fabrication of the samples starts with a silicon chip with a 285 nm thick thermally grown silicon dioxide layer. Dumbbell-shaped cavities with various diameters (Figure 1, parts a and b) are etched into the oxide layer using reactive ion etching with a depth of 300 nm. Single layer graphene grown by chemical vapor deposition is transferred on top of the sample using a support polymer. This polymer is dissolved and subsequently dried using critical point drying, which results in breaking of one side of the dumbbell and leaves a suspended resonator on the other end that is used for the experiment. The fabrication process is identical to that previously published in ref (39).

Figure 1.

Figure 1

Open in a new tab

Experimental setup. (a) Schematic figure of the sample used in the experiment. (b) Scanning electron microscope image of a successfully fabricated resonator, the top side of the dumbbell is broken and the bottom forms a resonator. (c) Laser interferometer setup used to actuate and readout the motion of the suspended graphene resonators. (d) Frequency sweeps at high modulation power, showing the Duffing response and the bistable region. During measurements, the frequency is fixed in the center of the bistable region after finding the two saddle-node bifurcations indicated by SN in the figure. z is the amplitude of the motion and R is the drum radius. The dimensionless frequency is ΩF/ω, ω and ΩF being the resonance frequency (ω = 2π × 13.92 × 106 rad/s) and the drive frequency, respectively. (e) Measured single sided power spectral density of the resonator’s amplitude at different noise levels (expressed as effective fluctuation temperature). (f) Mean square amplitude of resonance as a function of applied noise power, this graph is used as calibration to extract the effective temperature.

Figure 1c shows a schematic representation of the experimental setup used to actuate and detect the motion of single-layer graphene membranes. The red helium–neon laser with a power of 2 mW (measured before the objective) is used to detect the motion of the membranes and the amplitude of motion is calibrated using nonlinear optical transduction.40 The blue (405 nm, 0.1 mW) power-modulated diode laser thermally actuates the movement of the membrane, which can easily reach the bistable geometrically nonlinear regime.31,39 A vector network analyzer (VNA, Rohde and Schwarz ZNB4-K4) actuates the membrane by sweeping the frequency forward and backward and measures the amplitude and phase of the motion. The effective temperature of the resonator is artificially raised using an arbitrary waveform generator (AWG) that outputs white noise.

In order to quantify the effective temperature, the Brownian motion of the device is measured as a function of noise power outputted by the AWG (Figure 1, parts e and f). By fitting a Lorentzian to the measured PSD in Figure 1e and integrating this fit between frequency 0 and ∞, the mean square amplitude ⟨z2(t)⟩ of the device is derived which we use to define the effective temperature Teff:41

graphic file with name nl-2018-04862y_m001.jpg 1

where meff is the modal mass, ω is the resonance frequency, and kB is Boltzmann’s constant. The effective temperature is a means to express the fluctuation level in an intuitive manner: the fluctuations are identical to the thermal fluctuations of an undriven resonator at an actual temperature of T = Teff. The maximum obtained Teff = 65 × 103K, which was limited by the noise amplitude that can be applied by the AWG.

Since the amplitude is calibrated, the mean square amplitude at low fluctuation powers (where Teff ≈ T, T = 295 K being the environmental temperature) can also be used to determine the modal mass meff of the resonance. From the equipartition theorem:41

graphic file with name nl-2018-04862y_m002.jpg 2

we find meff = 1.85 fg. With the known modal mass, we can use the frequency response in Figure 1d to find the equation of motion. By fitting this frequency response, we find the dimensionless equation of motion:

graphic file with name nl-2018-04862y_m003.jpg 3

with ζ = 0.0012 the damping ratio, corresponding to a quality factor of 416.6, α = 200 the cubic stiffness coefficient and λ = 3 × 10–5. The fundamental frequency of the resonator is 13.92 MHz. The equation uses the generalized coordinate x(t) which represents the deflection of the membrane’s center normalized with respect to the membrane radius R = 2.5 μm. The definition of all the scaled variables, here employed to work only with relevant combinations of the parameters, are provided in the Supporting Information, part S1.

Before the experiment, the resonator is prepared in a bistable state as shown in Figure 1d. The frequency is swept forward and backward to reveal the hysteretic behavior of the device and the fixed drive frequency ωF is then set to be in the center between the two saddle-node bifurcations. During the experiment, the amplitude and phase of the resonator are probed as a function of time using the VNA set to a bandwidth of 10 kHz. There are now two signal sources driving the system: the fixed driving frequency from the VNA and the random fluctuations provided by the AWG. At a fluctuation power of approximately 25 × 103K the stochastic switching events are observed as shown in Figure 2(a). The amplitude x(t) is split into the in-phase (P) and out-of-phase (Q) part (x(t) = P(t) cos ωFt + Q(t) sin ωFt) as shown in Figure 2b, which reveals the two stable configurations of the resonator. Increasing the fluctuation power increases the switching rate as shown in Figure 2d at 65 × 103K. This also causes some broadening of the stable attractors, as can be seen from Figure 2e. Note that this figure does not give an accurate idea of the transition path due to the low bandwidth, higher bandwidth measurements that do reveal the transition path will be discussed in Figure 4. The experimentally observed switching rate, calculated by taking the inverse of the mean residence time in the stable attractors, as a function of the fluctuation power expressed in Teff is shown in Figure 2c. The experiment was repeated twice to check whether effects of slow frequency drift or other instabilities are affecting the experimental result, however both measurements show the same trend. From measurements on other mechanical systems in literature, we expect the switching rate between the stable attractors to follow Kramer’s law:8,13,24,38

graphic file with name nl-2018-04862y_m004.jpg 4

where rk is the transition rate from state k, ΔEk is an energy barrier, kB is the Boltzmann constant, and Ak is the maximum possible switching rate at high Teff. Fitting eq 4 to the experimentally observed transition rate in Figure 2c shows good agreement with the experimental result. From the fit, we obtain an energy barrier of 3.04 aJ and a maximum possible switching rate A = 17.5 kHz. To further investigate the transition dynamics of the system, we plot the distributions N for the residence times τhigh and τlow at 65 × 103 K as shown in Figure 2f. The residence time distribution should follow a Poisson distribution:8

graphic file with name nl-2018-04862y_m005.jpg 5

which is used to fit to the experimental data. The free parameter B arises from the normalization of the residence time distribution. From the fit, we find that the average transition time τ̅up = τ̅down = 1.7 ms, which corresponds to a transition rate of 0.58 kHz, matching the experimentally obtained value.

Figure 2.

Figure 2

Open in a new tab

Stochastic switching of the nonlinear resonator with a diameter of 5 μm. (a) Amplitude as a function of time for an effective temperature Teff = 25 × 103 K, showing a total of 8 fluctuation-induced transitions. The right-hand side of the figure shows a histogram of the amplitude. (b) Amplitude in the P-Q space for Teff = 25 × 103 K, each point is one sample of the measurement in part a. (c) Rate of up and down transitions as a function of effective temperature, fitted with Kramer’s law (eq 4), two sets of consecutive measurements are shown to check for consistency. (d) Amplitude as a function of time for an effective temperature Teff = 65 × 103 K, showing a total of 502 transitions. The right-hand side of the figure shows a histogram of the amplitude. (e) Amplitude in the P-Q space for Teff = 65 × 103 K. f) Residence time distributions for both states at Teff = 65 × 103, a Poisson distribution (eq 5) is fitted to the data and gives a transition time τk = 1.7 ms, corresponding to a transition rate rk = 0.58 kHz.

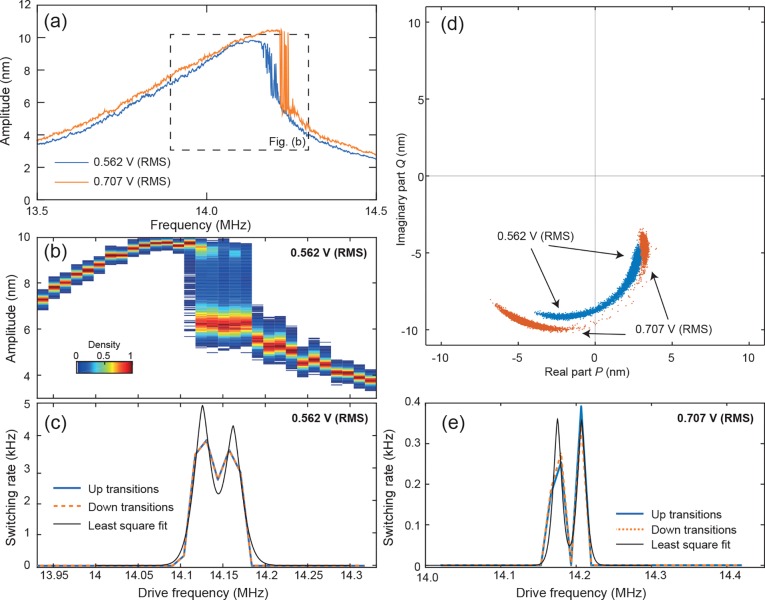
Figure 4.

Figure 4

Open in a new tab

Stochastic switching without additional noise on a different 3-μm diameter drum. (a) Forward frequency sweeps at two ac driving levels, showing stochastic switching in the bistable region. (b) Histogram of the amplitude at different fixed driving frequencies at 0.562 V (RMS) driving power. (c) Up and down switching rate as a function of fixed driving frequency with a drive amplitude of 0.562 V (RMS), including a least-square fit using eq 6. (d) P-Q-space of the amplitude for drive amplitude 0.562 V(RMS) at 14.131 MHz and for drive amplitude 0.707 V (RMS) at 14.18 MHz. (e) Up and down switching rate as a function of fixed driving frequency with a drive amplitude of 0.707 V (RMS), including a least-square fit using eq 6.

In order to further understand the dynamic behavior of the device, eq 3 is used to perform numerical simulations of the system in the presence of fluctuations to compare to the experimental results. We analyze the dynamics of the nonlinear oscillator using the method of averaging.18,42 This method describes the change of the vibration amplitude in time by ironing out the fast oscillations (see Supporting Information, part S1 for further details). Averaging is appropriate since the quality factor is high and the transition rate is much lower than the resonance frequency.

First, a linear stability analysis is performed for the deterministic system. The eigenvalues of the linearized system predicts two stable equilibria separated by an unstable equilibrium (a saddle). The original model is perturbed by adding a Gaussian white noise process, with intensity σ, details of which are shown in the Supporting Information, part S1. The intensity σ was matched to the experiments by evaluating the mean square amplitude due to the fluctuations ⟨x2(t)⟩ from the simulations and matching them to the experimentally measured mean square amplitude in Figure 1f. The stochastic switching behavior obtained via numerical integration of the stochastic differential equations can be seen in Figure 3.

Figure 3.

Figure 3

Open in a new tab

Simulations of stochastic switching of the nonlinear resonator in close agreement with the experiments in Figure 2. (a) Time evolution for a duration of 0.45 s of the stochastic system. Values for the plot are noise intensity σ = 0.000057 and integration step in the Euler–Maruyama method of dt = 15. A histogram of the distribution of the solution is shown on the right; (b) Density histogram of the solution for the long-term realization of the system of part a. Darker regions refer to states with a more probable occurrence. (c) Boxplot of the switching rate for the rate of up (blue) and down (orange) transitions as a function of noise intensity σ. The boxes limits are the 75% and 25% quantile, and the white marker is the median. (d) Time evolution of the stochastic system (σ = 0.000086, dt = 15). (e) Density histogram of the solution for the long-term realization of the system of part d. (f) Stream plot for the deterministic vector field (eq 5 of theSupporting Information) for the excitation frequency ωF = 1.0063. The white dots indicate the stable spirals while the gray dot point the saddle node.

We simulate a time evolution of the system as shown in Figure 3a, matching the time and effective temperature of the fluctuations of the experiment in Figure 2a. From these simulations, it can be seen that the large amplitude solution is the most probable state for the low-fluctuation configuration because the system resides for most of the time in the basin of attraction of this stable point (see the histogram in Figure 3a). Figure 3d, which corresponds to the measurement in Figure 2d, shows a massive number of transitions for the resonator with a more equal residence time distribution in the two separate states. The numerical prediction is in qualitative agreement with the switching density illustrated in Figure 2, parts a and d.

The linear stability analysis of our dynamical system unveils the existence and local properties of a given steady state.43 The deterministic skeleton of our system is shown in Figure 3(f), it presents 3 equilibria: eA = {0.002460,–0.000508}, eB = {−0.006008,–0.007784}, and eS = {0.006139,–0.005274} where eA and eB are in stable equilibrium but eS is a saddle point. The real part of the eigenvalues of the Jacobian for the stable equilibrium is the same for both the stable equilibrium points (−0.00012 ± 0.003769i for eA, −0.00012 ± 0.005318i for eB, and −0.004619 and 0.002219 for eS) suggesting that the points are equally stable. However, these equilibria under the influence of a stochastic dynamics can lose their property of stability turning in metastable attracting states.44 As a matter of fact, noise-induced fluctuations induce shifts between the metastable equilibria and thus inhibit us to infer the dynamical behavior out of the deterministic linear stability analysis. Parts a and d of Figure 3 show broad oscillations around the low-amplitude stable equilibrium, while more confined motion is observed around the high-amplitude equilibrium state. The density diagrams of the solution for the long-term (0.45 s) realization of the system are reported in Figure 3, parts b, c, and e.

At low-fluctuation levels (Figure 3b) the cloud spread is limited and the switching paths (blue and red paths in Figure 3b) are concentrated in crossing the saddle (gray dot in Figure 3f). The direction of the trajectories is in full accordance with the rotation of the orbits predicted by the stability analysis. Figure 3e illustrates a set of paths used by the system to revert its states. Moreover, it shows a larger spread in the phase-space, due to stronger excitation of slow-dynamics around each of the fixed points, besides the higher frequency stochastic switching between low and high-amplitude states. Finally, the switching rate as a function of the intensity of the additive Gaussian noise is reported in Figure 3c. The up and down transition rates are found to be similar and in accordance with the experimental findings.

Our experiments show high-frequency stochastic switching at lower effective temperatures. It is interesting to investigate how the system can be engineered to increase the switching rate further, for example to 20 kHz for microphone applications, while reducing the temperature of the fluctuations to room temperature. To reduce the effective temperature, from eq 4 one needs to reduce the energy barrier ΔEk. Near the saddle node bifurcations, this barrier scales as |ωF – ωk|ξ where ωk is the frequency of the bifurcation and ξ = 3/2 the critical exponent.45−47 ΔEk thus reduces to zero near the bifurcation points and this should significantly increase the switching rate according to eq 4. Furthermore, near the bifucation points, the energy barrier also scales approximately as ΔE ∝ λ2.45 This shows that the driving force should be minimized, which can be achieved by driving the system slightly above the critical force, which is the minimal force where the system first shows instability.

To qualitatively show that minimizing λ and choosing a frequency close to the saddle node bifurcations result in high-frequency stochastic switching at lower temperatures, we perform an additional experiment on a different 3-μm diameter drum in Figure 4. The bandwidth on the VNA was set to a high value of 1 MHz, to reveal the higher switching rate compared to Figure 2 (except Figure 4a, which was performed with a 10 kHz bandwidth). We drive the system at two different driving levels as shown in Figure 4a; 0.562 V is almost above the critical forcing amplitude where the system becomes unstable. At these low driving levels, stochastic switching events are readily observed without adding noise to the system. To determine the switching rates, the amplitude was recorded as a function of time at several fixed frequencies, while keeping the drive amplitude constant. Figure 4b shows the histogram of the amplitude at different fixed driving frequencies for the 0.562 V drive amplitude and Figure 4c shows the corresponding up and down switching rates. Increasing the drive amplitude separates the two stable attractors as shown in Figure 4d. This figure also reveals the paths of the transitions, which can be revealed due to the higher bandwidth of the measurement. The higher driving level of 0.707 V decreases the switching rate drastically, as shown in Figure 4e, showing that driving the resonator as close to the critical force as possible results in a higher switching rate.

We also observe in parts c and e of Figure 4 that in the vicinity of the saddle node bifurcations the observed transition rate is higher (Figure 4c,e), as expected. A least-square fit is performed to the data using the equation:

graphic file with name nl-2018-04862y_m006.jpg 6

where ωSN is the frequency of the saddle node bifurcation. These fits are included as black lines in parts c and e of Figure 4. Due to the limited frequency resolution of the measurement, this fit only provides rough estimates. However, we find the coefficients bk between 3 × 10–8 to 9 × 10–8. A bit further away from the saddle node bifurcations this results in energy barriers in the order of ∼0.1 aJ. Considering the scaling of the amplitudes that was performed in this measurement compared to Figure 2, this is a reasonable order of magnitude.

Close to the critical force we observe a maximum switching rate of 4063 Hz. The state-of-the-art in conventional MEMS devices achieved a 30 Hz switching rate at an effective temperature of 1.2 × 106 K,24 we have thus improved the switching rate by a factor of ∼100. For the effective temperature, we have to consider that the laser increases the temperature of the graphene drum somewhat. We make a rough estimate of the absorbed laser power to be 0.1 mW, based on the incident laser powers. From measurements on similar sized drums in literature48 we estimate the maximum temperature in the drum to be roughly 400 K. The temperature of the fluctuations has thus been lowered by a factor of at least 3000.

In conclusion, we have demonstrated kHz range stochastic switching on graphene drum resonators. The switching rate is 2 orders of magnitude higher, while the effective temperature of the fluctuations is 3 orders of magnitude lower than in state-of-the-art MEMS devices. Simulations of the system’s slow dynamics provide qualitative understanding of the stochastic behavior of the dynamical system. Further work can focus on increasing the switching rate and lowering of the fluctuation threshold energy ΔE to enable high-bandwidth (>10 kHz), stochastic switching enhanced, sensing at room temperature.

Acknowledgments

The authors thank Applied Nanolayers B.V. for the supply and transfer of single-layer graphene. We acknowledge Y. M. Blanter for useful discussions. This work is part of the research programme Integrated Graphene Pressure Sensors (IGPS) with Project Number 13307 which is financed by The Netherlands Organisation for Scientific Research (NWO). The research leading to these results also received funding from the European Union’s Horizon 2020 research and innovation program under Grant Agreement No. 785219 Graphene Flagship. F.A. acknowledges support from European Research Council (ERC) Grant Number 802093.

Supporting Information Available

This material is available free of charge via the Internet at http://pubs.acs.org/. The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.nanolett.8b04862.

  • Derivation of the stochastic differential equations used in the simulations (PDF)

Author Present Address

Second Institute of Physics, RWTH Aachen University, 52074 Aachen, Germany

Author Present Address

§ NTT Basic Research Laboratories, NTT Corporation, 3-1, Morinosato Wakamiya, Atsugi, Kanagawa 243-0198, Japan

The authors declare no competing financial interest.

Supplementary Material

nl8b04862_si_001.pdf (239.2KB, pdf)

References

  1. Wiesenfeld K.; Moss F. Stochastic Resonance and the Benefits of Noise: From Ice Ages to Crayfish and SQUIDs. Nature 1995, 373, 33–36. 10.1038/373033a0. [DOI] [PubMed] [Google Scholar]
  2. Russell D. F.; Wilkens L. A.; Moss F. Use of Behavioural Stochastic Resonance by Paddle Fish for Feeding. Nature 1999, 402, 291–294. 10.1038/46279. [DOI] [PubMed] [Google Scholar]
  3. Longtin A.; Bulsara A.; Moss F. Time-Interval Sequences in Bistable Systems and the Noise-Induced Transmission of Information by Sensory Neurons. Phys. Rev. Lett. 1991, 67, 656–659. 10.1103/PhysRevLett.67.656. [DOI] [PubMed] [Google Scholar]
  4. McNamara B.; Wiesenfeld K.; Roy R. Observation of Stochastic Resonance in a Ring Laser. Phys. Rev. Lett. 1988, 60, 2626–2629. 10.1103/PhysRevLett.60.2626. [DOI] [PubMed] [Google Scholar]
  5. Hibbs A.; Singsaas A.; Jacobs E.; Bulsara A.; Bekkedahl J.; Moss F. Stochastic Resonance in a Superconducting Loop With a Josephson Junction. J. Appl. Phys. 1995, 77, 2582–2590. 10.1063/1.358720. [DOI] [Google Scholar]
  6. Spano M.; Wun-Fogle M.; Ditto W. Experimental Observation of Stochastic Resonance in a Magnetoelastic Ribbon. Phys. Rev. A: At., Mol., Opt. Phys. 1992, 46, 5253–5256. 10.1103/PhysRevA.46.5253. [DOI] [PubMed] [Google Scholar]
  7. Rouse R.; Han S.; Lukens J. Flux Amplification Using Stochastic Superconducting Quantum Interference Devices. Appl. Phys. Lett. 1995, 66, 108–110. 10.1063/1.114161. [DOI] [Google Scholar]
  8. Gammaitoni L.; Hänggi P.; Jung P.; Marchesoni F. Stochastic Resonance. Rev. Mod. Phys. 1998, 70, 223–287. 10.1103/RevModPhys.70.223. [DOI] [Google Scholar]
  9. Lapidus L.; Enzer D.; Gabrielse G. Stochastic Phase Switching of a Parametrically Driven Electron in a Penning trap. Phys. Rev. Lett. 1999, 83, 899–902. 10.1103/PhysRevLett.83.899. [DOI] [Google Scholar]
  10. Hales J.; Zhukov A.; Roy R.; Dykman M. Dynamics of Activated Escape and its Observation in a Semiconductor Laser. Phys. Rev. Lett. 2000, 85, 78–81. 10.1103/PhysRevLett.85.78. [DOI] [PubMed] [Google Scholar]
  11. Tretiakov O.; Matveev K. Stochastic Current Switching in Bistable Resonant Tunneling Systems. Phys. Rev. B: Condens. Matter Mater. Phys. 2005, 71, 165326. 10.1103/PhysRevB.71.165326. [DOI] [Google Scholar]
  12. Wilkowski D.; Ringot J.; Hennequin D.; Garreau J. C. Instabilities in a Magneto-Optical Trap: Noise-Induced Dynamics in an Atomic System. Phys. Rev. Lett. 2000, 85, 1839–1842. 10.1103/PhysRevLett.85.1839. [DOI] [PubMed] [Google Scholar]
  13. Ricci F.; Rica R. A.; Spasenović M.; Gieseler J.; Rondin L.; Novotny L.; Quidant R. Optically Levitated Nanoparticle as a Model System for Stochastic Bistable Dynamics. Nat. Commun. 2017, 8, 15141. 10.1038/ncomms15141. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Rondin L.; Gieseler J.; Ricci F.; Quidant R.; Dellago C.; Novotny L. Direct Measurement of Kramers Turnover With a Levitated Nanoparticle. Nat. Nanotechnol. 2017, 12, 1130–1133. 10.1038/nnano.2017.198. [DOI] [PubMed] [Google Scholar]
  15. Levin J. E.; Miller J. P. Broadband Neural Encoding in the Cricket Cereal Sensory System Enhanced by Stochastic Resonance. Nature 1996, 380, 165–168. 10.1038/380165a0. [DOI] [PubMed] [Google Scholar]
  16. Douglass J. K.; Wilkens L.; Pantazelou E.; Moss F. Noise Enhancement of Information Transfer in Crayfish Mechanoreceptors by Stochastic Resonance. Nature 1993, 365, 337–340. 10.1038/365337a0. [DOI] [PubMed] [Google Scholar]
  17. Stambaugh C.; Chan H. B. Noise-Activated Switching in a Driven Nonlinear Micromechanical Oscillator. Phys. Rev. B: Condens. Matter Mater. Phys. 2006, 73, 172302. 10.1103/PhysRevB.73.172302. [DOI] [Google Scholar]
  18. Dykman M.; Maloney C.; Smelyanskiy V.; Silverstein M. Fluctuational Phase-flip Transitions in Parametrically Driven Oscillators. Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top. 1998, 57, 5202–5212. 10.1103/PhysRevE.57.5202. [DOI] [Google Scholar]
  19. Chan H.; Dykman M. I.; Stambaugh C. Paths of Fluctuation Induced Switching. Phys. Rev. Lett. 2008, 100, 130602. 10.1103/PhysRevLett.100.130602. [DOI] [PubMed] [Google Scholar]
  20. Badzey R. L.; Mohanty P. Coherent Signal Amplification in Bistable Nanomechanical Oscillators by Stochastic Resonance. Nature 2005, 437, 995–998. 10.1038/nature04124. [DOI] [PubMed] [Google Scholar]
  21. Aldridge J.; Cleland A. Noise-Enabled Precision Measurements of a Duffing Nanomechanical Resonator. Phys. Rev. Lett. 2005, 94, 156403. 10.1103/PhysRevLett.94.156403. [DOI] [PubMed] [Google Scholar]
  22. Chan H.; Stambaugh C. Fluctuation-Enhanced Frequency Mixing in a Nonlinear Micromechanical Oscillator. Phys. Rev. B: Condens. Matter Mater. Phys. 2006, 73, 224301. 10.1103/PhysRevB.73.224301. [DOI] [Google Scholar]
  23. Ono T.; Yoshida Y.; Jiang Y.-G.; Esashi M. Noise-Enhanced Sensing of Light and Magnetic Force Based on a Nonlinear Silicon Microresonator. Appl. Phys. Express 2008, 1, 123001. 10.1143/APEX.1.123001. [DOI] [Google Scholar]
  24. Venstra W. J.; Westra H. J.; Van Der Zant H. S. Stochastic Switching of Cantilever Motion. Nat. Commun. 2013, 4, 2624. 10.1038/ncomms3624. [DOI] [PubMed] [Google Scholar]
  25. Novoselov K.; Jiang D.; Schedin F.; Booth T.; Khotkevich V.; Morozov S.; Geim A. Two-Dimensional Atomic Crystals. Proc. Natl. Acad. Sci. U. S. A. 2005, 102, 10451–10453. 10.1073/pnas.0502848102. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Geim A. K.; Novoselov K. S. The Rise of Graphene. Nat. Mater. 2007, 6, 183–191. 10.1038/nmat1849. [DOI] [PubMed] [Google Scholar]
  27. Lee C.; Wei X.; Kysar J. W.; Hone J. Measurement of the Elastic Properties and Intrinsic Strength of Monolayer Graphene. Science 2008, 321, 385–388. 10.1126/science.1157996. [DOI] [PubMed] [Google Scholar]
  28. Bunch J. S.; van der Zande A. M.; Verbridge S. S.; Frank I. W.; Tanenbaum D. M.; Parpia J. M.; Craighead H. G.; McEuen P. L. Electromechanical Resonators from Graphene Sheets. Science 2007, 315, 490–493. 10.1126/science.1136836. [DOI] [PubMed] [Google Scholar]
  29. Chen C.; Rosenblatt S.; Bolotin K. I.; Kalb W.; Kim P.; Kymissis I.; Stormer H. L.; Heinz T. F.; Hone J. Performance of Monolayer Graphene Nanomechanical Resonators With Electrical Readout. Nat. Nanotechnol. 2009, 4, 861–867. 10.1038/nnano.2009.267. [DOI] [PubMed] [Google Scholar]
  30. Davidovikj D.; Alijani F.; Cartamil-Bueno S. J.; van der Zant H. S. J.; Amabili M.; Steeneken P. G. Nonlinear Dynamic Characterization of Two-Dimensional Materials. Nat. Commun. 2017, 8, 1253. 10.1038/s41467-017-01351-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Dolleman R. J.; Houri S.; Chandrashekar A.; Alijani F.; van der Zant H. S.; Steeneken P. G. Opto-Thermally Excited Multimode Parametric Resonance in Graphene Membranes. Sci. Rep. 2018, 8, 9366. 10.1038/s41598-018-27561-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Bunch J. S.; Verbridge S. S.; Alden J. S.; Van Der Zande A. M.; Parpia J. M.; Craighead H. G.; McEuen P. L. Impermeable Atomic Membranes From Graphene Sheets. Nano Lett. 2008, 8, 2458–2462. 10.1021/nl801457b. [DOI] [PubMed] [Google Scholar]
  33. Smith A.; Niklaus F.; Paussa A.; Vaziri S.; Fischer A. C.; Sterner M.; Forsberg F.; Delin A.; Esseni D.; Palestri P.; Ostling M.; Lemme M. Electromechanical Piezoresistive Sensing in Suspended Graphene Membranes. Nano Lett. 2013, 13, 3237–3242. 10.1021/nl401352k. [DOI] [PubMed] [Google Scholar]
  34. Dolleman R. J.; Davidovikj D.; Cartamil-Bueno S. J.; van der Zant H. S.; Steeneken P. G. Graphene Squeeze-Film Pressure Sensors. Nano Lett. 2016, 16, 568–571. 10.1021/acs.nanolett.5b04251. [DOI] [PubMed] [Google Scholar]
  35. Eichler A.; Moser J.; Chaste J.; Zdrojek M.; Wilson-Rae I.; Bachtold A. Nonlinear Damping in Mechanical Resonators Made From Carbon Nanotubes and Graphene. Nat. Nanotechnol. 2011, 6, 339–342. 10.1038/nnano.2011.71. [DOI] [PubMed] [Google Scholar]
  36. Koenig S. P.; Wang L.; Pellegrino J.; Bunch J. S. Selective Molecular Sieving Through Porous Graphene. Nat. Nanotechnol. 2012, 7, 728–732. 10.1038/nnano.2012.162. [DOI] [PubMed] [Google Scholar]
  37. Dolleman R. J.; Cartamil-Bueno S. J.; van der Zant H. S. J.; Steeneken P. G. Graphene Gas Osmometers. 2D Mater. 2017, 4, 011002. 10.1088/2053-1583/4/1/011002. [DOI] [Google Scholar]
  38. Kramers H. A. Brownian Motion in a Field of Force and the Diffusion Model of Chemical Reactions. Physica 1940, 7, 284–304. 10.1016/S0031-8914(40)90098-2. [DOI] [Google Scholar]
  39. Dolleman R. J.; Houri S.; Davidovikj D.; Cartamil-Bueno S. J.; Blanter Y. M.; van der Zant H. S.; Steeneken P. G. Optomechanics for Thermal Characterization of Suspended Graphene. Phys. Rev. B: Condens. Matter Mater. Phys. 2017, 96, 165421. 10.1103/PhysRevB.96.165421. [DOI] [Google Scholar]
  40. Dolleman R. J.; Davidovikj D.; van der Zant H. S. J.; Steeneken P. G. Amplitude Calibration of 2D Mechanical Resonators by Nonlinear Optical Transduction. Appl. Phys. Lett. 2017, 111, 253104. 10.1063/1.5009909. [DOI] [Google Scholar]
  41. Hauer B.; Doolin C.; Beach K.; Davis J. A General Procedure for Thermomechanical Calibration of Nano/Micro-Mechanical Resonators. Ann. Phys. 2013, 339, 181–207. 10.1016/j.aop.2013.08.003. [DOI] [Google Scholar]
  42. Kryloff N.; Bogoliubov N.; Lefschetz S.. Introduction to Non-linear Mechanics; Annals of Mathematics Studies; Princeton University Press: 1947. [Google Scholar]
  43. Strogatz S. H.Nonlinear Dynamics and Chaos: With Applications to Physics, Biology, Chemistry, and Engineering; CRC Press: 2018. [Google Scholar]
  44. Zhou J. X.; Aliyu M. D. S.; Aurell E.; Huang S. Quasi-Potential Landscape in Complex Multi-Stable Systems. J. R. Soc., Interface 2012, 9, 3539–3553. 10.1098/rsif.2012.0434. [DOI] [PMC free article] [PubMed] [Google Scholar]
  45. Dykman M.; Krivoglaz M. Theory of Fluctuational Transitions Between Stable States of a Nonlinear Oscillator. Sov. Phys. JETP 1979, 50, 30–37. [DOI] [PubMed] [Google Scholar]
  46. Chan H. B.; Stambaugh C. Activation Barrier Scaling and Crossover for Noise-Induced Switching in Micromechanical Parametric Oscillators. Phys. Rev. Lett. 2007, 99, 060601. 10.1103/PhysRevLett.99.060601. [DOI] [PubMed] [Google Scholar]
  47. Defoort M.; Puller V.; Bourgeois O.; Pistolesi F.; Collin E. Scaling Laws for the Bifurcation Escape Rate in a Nanomechanical Resonator. Phys. Rev. E 2015, 92, 050903. 10.1103/PhysRevE.92.050903. [DOI] [PubMed] [Google Scholar]
  48. Cai W.; Moore A. L.; Zhu Y.; Li X.; Chen S.; Shi L.; Ruoff R. S. Thermal Transport in Suspended and Supported Monolayer Graphene Grown by Chemical Vapor Deposition. Nano Lett. 2010, 10, 1645–1651. 10.1021/nl9041966. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

nl8b04862_si_001.pdf (239.2KB, pdf)

Articles from Nano Letters are provided here courtesy of American Chemical Society

RESOURCES