Figure 1.

Constraint-based modeling of metabolic networks. A, A metabolic network is a collection of biochemical reactions exchanging metabolites with the environment and interconverting them into the building blocks of biomass and energy. The network includes five reactions and four metabolites, A to D. B, Stoichiometric matrix of the metabolic network shown in A. Highlighted is reaction 2, converting one molecule of the substrate B into one molecule of the product C. C, Feasible solutions (gray) are compatible with the steady-state constraints, whereby there is no change in the concentration of metabolite over time (i.e. 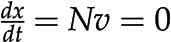) and flux capacity bounds (i.e. ). 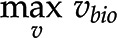The optimum for the objective function, , in orange is associated with a unique optimum flux distribution (v*), while 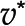and 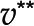are two optimal flux distributions for the objective function in blue. Note that the optimal objective value at 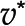and 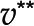are the same. D, Addition of reactions 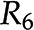and 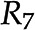leads to the introduction of metabolite E. E, Removal of reaction 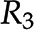leads to the removal of metabolite D. F, Context-specific metabolic networks are obtained by considering constraints from different profiling technologies applicable to single cell types, tissues, organs, and entire organisms.