Constructing Atomic Structural Models into Cryo-EM Densities using Molecular Dynamics - Pros and Cons

Abstract

Accurate structure determination from electron density maps at 3-5 Å resolution necessitates a balance between extensive global and local sampling of atomistic models, yet with stereochemical correctness of backbone and sidechain geometries. Molecular Dynamics Flexible Fitting (MDFF), particularly through a resolution-exchange scheme, ReMDFF, provides a robust way of achieving this balance for hybrid structure determination. Employing two high-resolution density maps, namely that of β-galactosidase at 3.2 Å and TRPV1 at 3.4 Å, we showcase the quality of ReMDFF-generated models, comparing them against ones submitted by independent research groups for the 2015-2016 Cryo-EM Model Challenge. This comparison offers a clear evaluation of ReMDFF’s strengths and shortcomings, and those of data-guided real-space refinements in general. ReMDFF results scored highly on the various metric for judging the quality-of-fit and quality-of-model. However, some systematic discrepancies are also noted employing a Molprobity analysis, that are reproducible across multiple competition entries. A space of key refinement parameters is explored within ReMDFF to observe their impact within the final model. Choice of force field parameters and initial model seem to have the most significant impact on ReMDFF model-quality. To this end, very recently developed CHARMM36m force field parameters provide now more refined ReMDFF models than the ones originally submitted to the Cryo-EM challenge. Finally, a set of good-practices is prescribed for the community to benefit from the MDFF developments.

Introduction

Cryo-electron microscopy (cryo-EM) has emerged to be one of the most successful structure determination methods, achieving in recent years unprecedented resolution that challenges the capabilities of more traditional techniques such as, X-ray diffraction, electron or neutron scattering, and NMR (Wlodawer et al., 2017). Notably, cryo-EM based structure determination overcomes three major bottlenecks faced in X-ray crystallography: first, the very process of growing micronsized crystals for a sample can be time-consuming or even unachievable (Unger, 2002), second, crystallized macromolecules and the resulting structures often show biologically irrelevant features imposed by the crystal lattice contacts (Neutze et al., 2015), and third, larger unit cells are more susceptible to whole-molecule disorder and therefore lower structural resolution (Frank, 2002, Singharoy et al., 2015). Benefiting from the use of direct-detection cameras (Li et al., 2013, Milazzo et al., 2011), and high-throughput particle picking and clustering techniques (Scheres, Tang et al., 2007), cryo-EM provides today a natural way of resolving structural snapshots from vitrified samples of large soluble or membrane-embedded macromolecular complexes in action.

Real-space refinement schemes have been instrumental in interpreting low-resolution electron-density data with all-atom details procured either from homology models, existing crystal structures, or de novo structure building. Showcasing an array of methodological advances, these schemes employ rigid-fragment fitting (Van Zundert and Bonvin, 2016), low-frequency normal modes (Gorba et al., 2008), deformable elastic networks (Schröder et al., 2014), cross-correlation or least-squares difference between experimental and simulated maps (Lopéz-Blanco and Chacón,2013, Tama et al., 2004), phenomenological force fields (DiMaio et al., 2015), backbone tracing (Chen et al., 2016), crystallographic structure factors (Terwilliger et al., 2018), and Molecular Dynamics (MD) simulations (McGreevy et al., 2016). Available within popular software suites such as DireX (Schröder et al., 2007), Flex-EM (Topf et al., 2008), Rosetta (DiMaio et al., 2015), FRODA (Jolley et al., 2008), Refmac (Brown et al., 2015), Phenix (Afonine et al., 2013) and Molecular Dynamics Flexible Fitting (MDFF) (Trabuco et al., 2008), the real-space methodologies have successfully solved structures across 3 to 15 Å resolution range.

MDFF, in particular, has proven to be successful in the hands of its developers as evidenced by applications to solving structural models for the ribosomal machinery (Villa et al., 2009, Trabuco et al., 2011, Frauenfeld et al., 2011, Wickles et al., 2014), photosynthetic proteins (Hsin et al., 2010), myosin (Kim et al., 2010), chaperonins (Zhang et al., 2013), bacterial chemosensory array (Cassidy et al., 2015), and most recently membrane channel proteins (Chen et al., 2017). MDFF has played an even greater role in structural modeling efforts outside of its developer group, namely for the ribosome and its substrates (Gogala et al., 2014, Becker et al., 2012, Parker and Newstead, 2014), the actin-myosin interface (Lorenz and Holmes, 2010), the Mot1-TBP complex (Wollmann et al., 2011), the 26S proteasome (Unverdorben et al., 2014), and the non-enveloped viruses (Schur et al., 2015).

Notwithstanding the aforementioned advances, high-resolution maps pose an imminent challenge to the traditional map-guided structure-determination schemes, including MDFF, as the maps now characterize near-atomic scale features, the interpretation of which requires extremely precise structure building and validation protocols. For example, conformation of the protein sidechains, which are more flexible than the backbone, are now discernible within the maps and, thus, require precise modeling of the dihedral angles up to Cβ atoms while also respecting the map boundaries. Accuracy of the sidechain structure determines the biological relevance of a model. In order to produce such atomic models with correct backbone and sidechain geometries, as well as minimal potential energy, MDFF was augmented with density-guided enhanced sampling algorithms (Singharoy et al., 2016). Denoted resolution exchange MDFF (ReMDFF), this method sequentially re-refines a search model against a series of maps of progressively higher resolutions, which ends with the original experimental resolution. Flexible-fitting to the lower resolution maps provides the overall model topology, whereas backbone and sidechain refinements are guided by intermediate to high-resolution maps. Application of the sequential re-refinement enabled ReMDFF to achieve a radius of convergence of 25 Å, demonstrated with the accurate modeling of β-galactosidase and TRPV1 proteins at 3.2 Å and 3.4 Å resolution. Due to issues with unphysical entrapment in energy minima from local density features, traditional MDFF is incapable of modeling for such high-resolution EM densities (Singharoy et al., 2016).

In this article, we provide a detailed analysis of the models derived from ReMDFF refinements. First, the flexible fitting methodology is outlined (Methods). Second, quality of the ReMDFF-generated models are ascertained for two high-resolution density maps, namely that of β-galactosidase (EMD-5995) of reported resolution 3.2 Å and TRPV1 channel (EMD-5778) of reported resolution 3.4 Å (Results: ReMDFF refinements). These ReMDFF models are compared to those from the submissions of independent researchers accrued over the 2015-2016 EMDataBank Model Challenge (Lawson et al., 2018). The comparative analysis allows the identification of strengths and weaknesses within our flexible-fitting strategy (Results: Comparison with submitted models from the modeling challenge). Thereafter, three refinement parameters are examined to judge their impact on the quality of ReMDFF results - force field parameters in the MD simulation, strength of forces derived from the EM densities for flexible fitting of a model, and the quality of secondary structure in the initial models (Results: Parameter dependence). To the best of our knowledge, this article presents the first instance of a systematic analysis of force field parameters within MDFF. Finally, we come up with a prescription for the use of MDFF methods with high-resolution density maps (Discussion).

Methods

Traditional and resolution-exchange MDFF methodologies are described in the following. Thereafter a computational protocol is outlined that leverages these refinement methodologies within the popular molecular dynamics platform NAMD (Phillips et al., 2005).

Traditional MDFF

MDFF requires, as input data, an initial structure and a cryo-EM density map. A potential map is generated from the density and subsequently used to bias an MD simulation of the initial structure. The structure is subject to the EM-derived potential while simultaneously undergoing structural dynamics as described by the MD force field.

Let the biasing potential associated with the EM map at a point r be Φ(r). Then the MDFF potential map is given by

$$V_{\text{EM}}(\mathbf{r})=\{\begin{array}{cc}\zeta \left(1-\frac{\Phi (\mathbf{r})-{\Phi }_{\text{thr}}}{{\Phi }_{\text{max}}-{\Phi }_{\text{thr}}}\right)\hfill & \text{if}\Phi (\mathbf{r})\ge {\Phi }_{\text{thr}},\hfill \\ \zeta \hfill & \text{if}\Phi (\mathbf{r})<{\Phi }_{\text{thr}}.\hfill \end{array}\phantom{\}}$$ (1)

where ζ is a scaling factor that controls the strength of the coupling of atoms to the MDFF potential, Φ_thr is a threshold for disregarding noise, and Φ_max = max(Φ(r)). The potential energy contribution from the MDFF forces is then

$$U_{\text{EM}}=\sum _i{w}_i{V}_{\text{EM}}({\mathbf{r}}_i),$$ (2)

where i labels the atoms in the structure, r_i represents its position, and w_i is an atom-dependent weight, usually the atomic mass.

During the simulation, the total potential acting on the system is given by

$$U_{\text{total}}=U_{\text{MD}}+U_{\text{EM}}+U_{\text{SS}}$$ (3)

where U_MD is the MD potential energy as provided by MD force fields, e.g., CHARMM, and U_SS is a secondary structure restraint potential that prevents warping of the secondary structure by the potentially strong forces due to U_EM. A detailed description of the potentials arising in Eq. 3 is given in references (Trabuco et al., 2008, 2009).

ReMDFF

In ReMDFF, an initial structure is fitted to a series of potential maps of successively higher resolution, with the final potential map being the original one derived from the EM map. Starting with i = 1, the ith map in the series is obtained by applying a Gaussian blur of width σ_i to the original potential map, such that σ_i decreases as the structure is fitted in the sequence i = 1, 2,…, L, where L is the total number of maps in the series, so that σ_L = 0 Å. The fitting protocol assumes a replica-exchange approach described as follows. Further details are provided in reference (Singharoy et al., 2016).

Replica Exchange MD (ReMD) is an advanced sampling method that explores conformational phase space in search of conformational intermediates, which are separated by energy barriers too high to be overcome readily by fixed temperature simulations. Instead of working with a single, fixed MD simulation, ReMD carries out many simulations in parallel, but at different temperatures T₁ < T₂ < T₃ < … where the lowest temperature T₁ is the temperature of actual interest, typically, room temperature. The simulations of several copies of the system, the so-called replicas, run mainly independently, such that ReMD can be easily parallelized on a computer, but at regular time points the instantaneous conformations of replicas of neighboring temperatures are compared in terms of energy and transitions between replicas are permitted according to the so-called Metropolis criterion (Sugita and Okamoto, 1999). This way the highest temperature replicas overcome the energy barriers between conformational intermediates and, through the Metropolis criterion, moves the T₁ replica from it such that transitions between intermediates occur frequently. The application of the Metropolis criterion in the protocol guarantees that the conformations of the T₁ replica are Boltzmann-distributed.

ReMDFF extends the concept of ReMD to MDFF by simply differentiating replicas not by temperatures T₁ < T₂ < T₃ < …, but by the half-width parameters σ₁ > σ₂ > σ₃ >. … Numerical experiments showed that ReMDFF works extremely well (Singharoy et al., 2016), as also documented in the present study. As NAMD can parallelize ReMD well (Jiang et al., 2014), it can do the same for ReMDFF, such that the enhanced sampling achieved translates into extremely fast MDFF convergence. At certain time instances replicas i and j, of coordinates xi and Xj and fitting maps of blur widths σ_i and σ_j, are compared energetically and exchanged with Metropolis acceptance probability

$$p({\mathbf{x}}_i,{\sigma }_i,{\mathbf{x}}_j,{\sigma }_j)=\text{min}\left(1,\text{exp}\left(\frac{-U({\mathbf{x}}_i,{\sigma }_j)-U({\mathbf{x}}_j,{\sigma }_i)+U({\mathbf{x}}_i,{\sigma }_i)+U({\mathbf{x}}_j,{\sigma }_j)}{k_{B}T}\right)\right),$$ (4)

where k_B is the Boltzmann constant, U(x, σ) is the instantaneous total energy of the configuration x within a fitting potential map of blur width σ. One can intuitively understand ReMDFF as fitting the simulated structure to an initially large and ergodic conformational space that is shrinking over the course of the simulation towards the highly corrugated space described by the original MDFF potential map.

Refinement protocol

The steps involved in performing an ReMDFF computation is described as follows: First, the reported map is smoothed employing Gaussian blurs with a range of half-widths, σ_i, to obtain a set of density maps, each characterizing a different local resolution. MDFF potentials V_EM are determined from each one of these maps employing Eq. 1. For example, 11 maps were generated at increasing σ_i of 0.5 Å to 5.5 Å to smooth the reported β-galactosidase and TRPV1 maps. Note, all refinements are performed with raw density data prior to sharpening. Second, an initial model is docked into the EM density employing a rigid-body protocol, e.g., with Situs (Wriggers, 2010) or Chimera (Pettersen et al., 2004). The most blurred density is chosen for this purpose. Two kinds of initial models are employed in the current study for highlighting ReMDFF refinement with different starting points - the experimentally reported models (Results: ReMDFF refinements) and thermally annealed models with lower secondary structural content (Results: Parameter dependence). These tests, together with past successful examples, imply that both homology as well as ab initio models can be employed as initial models in flexible fitting (Schweitzer et al., 2016, Wehmer et al., 2017, Monroe et al., 2017). Third, secondary-structure, chirality and cis-peptide restraints are generated from the initial model according to protocols defined in reference (Schreiner et al., 2011). Worth noting, the higher the quality of the initial model, the better is the quality of these restraints. Fourth, the force field, temperature and solvent conditions are chosen. ReMDFF can be performed with any standard classical force field available in NAMD, under various simulation conditions, including different temperatures and vacuum, membrane, and explicit or implicit solvent environments (Phillips et al., 2005). For most examples in the current article, an implicit solvent environment is chosen, and temperatures are set at 298 K, decreasing gradually to 0 K over 200 ps (McGreevy et al., 2014). NAMD configuration files are provided as supporting information to reproduce the list of input parameters in our ReMDFF refinements.

Finally, the resolution exchange program is invoked within NAMD, following the scheme in Figure 1. The map-model coupling parameter, ζ (denoted GSCALE in NAMD configuration files), is empirically set through the analysis of a few choices. This number is usually set to 0.3, but as noted below the choice changes marginally with force fields. A range of 0.3 to 0.6 is suggested, as larger ζ have been shown to induce over-fitting (McGreevy et al., 2016, Monroe et al., 2017). During ReMDFF, a nearest-neighboring resolution exchange is attempted every 1000 steps. Depending upon smoothness of the density, 60 - 90% exchange rate is achieved. The advantage of this protocol is that exchange between multiple resolutions allow simultaneous refinement of global and local structure - the lower resolution density maps allow large-scale motions to accommodate topological refinements in the structure, while the higher resolution maps allow for accurate placement of sidechains.

Fig. 1. A simple example of Resolution-exchange Molecular Dynamics Flexible Fitting (ReMDFF).

Three replicas are included in this schematic. Each replica consists of a molecular structure and a cryo-EM map-based grid potential. Different green boxes represents grid potentials of different resolutions. The structural models as refined at different resolutions are shown in red, blue, and yellow with different hue levels representing changes in the conformation. The arrows indicate the transfer of a grid potential from one replica to another. The output structure is selected from the trajectory visited by the grid potential of the original resolution (dark green).

All simulations where performed using NAMD2.12 for approximately 12 hours on a single workstation with the following specifications: 1 Nvidia Quadro P6000 GPU, and 16 Intel(R) Xeon(R) CPUs with the cumulative memory of 500 GB. In order to test for the overfitting, cross-validation using the EMRinger and the FSC analysis were performed after fitting the structures i e., β-galactosidase and TRPV1 onto two half-maps derived from the reported corresponding EM maps respectively (Bartesaghi et al., 2014, Liao et al., 2013). The iFSC and the EMRinger values for the both the direct and the cross comparisons are almost identical, indicating a very low degree of overfitting. Further details are provided in the previous work on fitting TRPV1 and β-galactosidase (Singharoy et al., 2016).

Results

First, a brief summary of ReMDFF refinements is provided. Thereafter, a comparative analysis of ReMDFF-derived structures is undertaken using data from the 2015-2016 Cryo-EM Model Challenge (Lawson et al., 2018, Kryshtafovych et al., 2018a). A number different metrics are compared, all of which are described by (Kryshtafovych et al., 2018b) and reported in the website for the competition models (Kryshtafovych et al., 2018a). Accuracy of the two ReMDFF test refinements is further explored within a space of three model-refinement parameters. Finally, a set of good practices is determined for the application of flexible fitting with high-resolution density maps.

ReMDFF refinements of β-galactosidase and TRPV1 structures

ReMDFF simulations were performed starting with the reported structures of β-galactosidase (Bartesaghi et al., 2014) and TRPV1 (Liao et al., 2013) at resolutions 3.2 Å and 3.4 Å respectively. The refinement statistics are provided as follows.

β-galactosidase The best ReMDFF model derived for β-galactosidase at 3.2 Å deviates from the reported structure marginally, by 0.6 Å root mean square deviation (RMSD); the overall map-model cross-correlation improved only by 1%. Nonetheless, a dramatic improvement is observed on the structural statistics of the model. Notably, the ReMDFF model has zero unfavorable clashes, 92.3% favored rotamers, 0.00% bad bonds, and an overall Molprobity score of 1.23, clear improvements over a clash-score of 90.8, 67.4% favored rotamer, 0.09% bad bonds and a Molprobity score of 3.14 in the initial model (Table 1A [CHARMM36 vs. Initial]). The number of cis-prolines and cis-nonprolines were not altered, potentially because the free-energy barrier for the associated transformation is around 2-3 kcal/mol (Wu, 2013), which cannot be sampled within the finite timescales of the ReMDFF refinements. The Ramachandran favored dihedrals are reduced by 1.5% to 95.8%. We describe later in the Results: Parameter dependence section, a strategy for resurrecting this minor loss in statistics.

Table 1.

Tables depicting the effect of different force fields on the MolProbity and EMRinger scores upon ReMDFF re-refinement of the experimentally deposited βGAL–PDBID:3J7H (A) and TRPV1-PDBID:3J5P (B) structures. The forcefields used were CHARMM36, CHARMM36m and OPLS. The numbers reported are in percentages (%). First column under Initial represents the the MolProbity and EMRinger attributes for the deposited structure. CHARMM36m provides the best geometries among these three force fields.

Table 1A: β-galactosidase
MolProbity Parameters	Initial	CHARMM36	CHARMM36m	OPLS
Poor rotamers (%)	11.6	3.89	2.6	4.23
Favored rotamers (%)	67.4	90.22	90.53	88.13
Ramachandran outliers (%)	0.2	0.69	0.59	0.49
Ramachandran favored (%)	97.4	95.78	96.45	94.95
Cβ deviations (%)	0.0	0.21	0.95	1.16
Bad bonds (%)	0.09	0.00	0.0	0.01
Bad angles (%)	0.03	0.92	0.73	1.14
Cis prolines (%)	8.06	8.06	8.06	8.06
Cis non-prolines (%)	1.15	1.15	1.15	1.15
Clash score	90.8	0.0	0.0	0.0
EMRinger	2.04	4.22	4.22	3.79
Table 1B: TRPV1
MolProbity Parameters	initial	CHARMM36	CHARMM36m	OPLS
Poor rotamers (%)	28.80	3.37	2.81	2.81
Favored rotamers (%)	53.80	90.5	90.75	90.50
Ramachandran outliers (%)	1.00	3.47	3.26	3.21
Ramachandran favored (%)	94.5	92.3	92.37	92.42
Cβ deviations (%)	0.0	0.53	0.65	0.65
Bad bonds (%)	0.72	0.0	0.26	0.27
Bad angles (%)	0.52	0.42	0.56	0.57
Cis prolines (%)	15.38	15.38	16.67	16.67
Cis non-prolines (%)	0.62	0.62	0.64	0.64
Clash score	92.8	0.0	0.0	0.0
EMRinger	0.56	1.75	2.25	2.54

TRPV1 Similar to β-galactosidase, the ReMDFF model of TRPV1 manifested major improvements in structural statistics within minor deviations from the reported model (RMSD of 1.1 Å). The clash score improved from 92.8 to 0, favored rotamers from 53.8% to 90.5%, bad bonds and angles decreased from 0.72% and and 0.52% to 0% and 0.42% (Table 1B). Overall Molprobity scores improved significantly from 3.92 to 1.34. As with β-galactosidase, the number of cis-prolines and cis-nonprolines in TRPV1 stemmed from the initial model, and the Ramachandran favored dihedrals marginally decreased.

Overall, both the β-galactosidase and TRPV1 results clearly depict the effect of minor structural changes on the quality of an EM model, as aptly captured by ReMDFF. Demonstrated in a separate article (Singharoy et al., 2016), efficient modeling of such details is beyond the capability of traditional MDFF. Thus, for high-resolution maps ReMDFF provides the most appropriate flexible-fitting protocol within NAMD.

Comparison with submitted models from modeling challenge

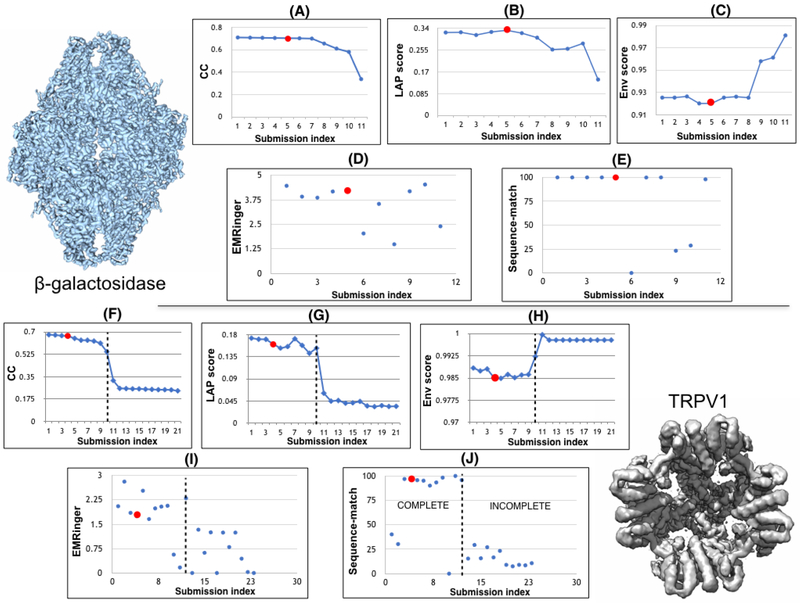
The 2015-2016 EMDataBank Model Challenge (Lawson et al., 2018) provides a perfect opportunity for comparing the quality of our ReMDFF-derived structures with those submitted by other teams. Worth noting, the ensemble of structures for a given biological system available through this competition represents on one hand, the outcome of a diversity of refinement methodologies, while on the other, variations in user expertise. Thus, it is possible that the same methodology in the hand of different users has produced varied submissions for a particular biological system. This apparent uncertainty is expected to assist an unbiased comparison of results. Continuing from the Results: ReMDFF refinements section, we will focus on models with the β-galactosidase and TRPV1 data. The former featured 23 submissions, while the latter had 11, including the ones from us reported in the previous section. Four different measures are reported to showcase the accuracy of ReMDFF in capturing structural features across a range of spatial scales.

Cross-correlation coefficient First, the quality of global fit is analyzed in terms of cross-correlation (CC) metrics, such as Envelope score (denoted ENV), cross-correlation coefficient (denoted CCC), and Laplacian filtered correlation coefficient (denoted LAP) (Kryshtafovych et al., 2018b). While ENV and CCC provide an idea of the global consistency between the map and the model by measuring respectively, the overlap between the map and the model, and the amount of filled vs. empty spaces within the model-fitted map, LAP is more sensitive to local features, such as the similarity between the map and model surface (Ozenbaugh and Pullen, 2017). Consequently, for a given map-model combination LAP values are always lesser than CCC and ENV.

Presented in Figure 2, the CC scores clearly stratified the submitted results in two classes. ReMDFF results are consistently scored high, found in the upper rung of the plots. Existence of the two classes of results stems from a difference in sequence match - complete models with near-100% sequence match, such as from ReMDFF, always exhibit better CC scores than incomplete ones featuring 10-20% sequence match. However, models with higher CCC and LAP have relatively lower ENV, though the differences in ENV scores of the models are much lesser than those of the two other metrics. This is because, the incomplete models only fit the density segments they could interpret, which naturally produces marginally higher ENV values than the complete models that encompass the entire density map. Our local cross correlation analysis presented in Fig. S2, further supports the high-fidelity of MDFF results, showing refinement at the individual residue level.

Fig. 2. 2015-2016 Cryo-EM challenge results.

Model-fit and -quality scores are provided for competetion entries of β-galactosidase (upper pannels) and TRPV1 (lower panels) models. ReMDFF results are circled in red. The measures presented include correlation coefficients (CC) (A,F), Laplacian filtered correlation coefficient (LAP) (B,G), envelope score (ENV) (C,H), EMRinger scores (D,I) and sequence-match (E,J). Detailed in the article, ReMDFF results are consistently high-socing across these range of metrics.

LAP scores for β-galactosidase are always higher than those of TRPV1, implying the local resolution of the former is higher, which allows for better recognition of the surface features. As expected, the higher-resolution map of β-galactosidase facilitated the submission of a greater population of complete models.

MolProbity statistics Second, the quality of model stereochemistry is judged based on their MolProbity statistics. Details on MolProbity scoring strategies is discussed in references (Davis et al., 2007, Chen et al., 2010). Most of the models reported > 90% Ramachandran-favored backbone dihedral angles for β-galactosidase, but only a quarter of the submissions achieved the same for TRPV1 (Table 2 A-B). ReMDFF consistently achieved this > 90% benchmark for both maps, again appearing in the upper rung of the reported models.

Table 2.

Table describing model-quality metrics for the β-galactosidase (A) and TRPV1 (B) structures deposited to the Cryo-EM challenge (http://model-compare.emdatabank.org). The attributes that are depicted are favored Ramachandran, rotamer outliers, Ramachandran outlier and mutual information. The numbers shown are in percentages (%). The ReMDFF models (Model 5 for β-galactosidase and Model 4 for TRPV1) are depicted in bold face.

Table 2A: β-galactosidase
Model	Rama Favored (%)	Rotamer outliers (%)	Rama outliers (%)	Mutual info.
Model 1	96.67	0.46	0.00	0.17538
Model 2	97.35	1.37	0.20	0.17613
Model 3	98.14	0.00	0.00	0.17388
Model 4	93.95	0.35	0.00	0.17646
Model 5	95.78	3.89	0.69	0.17813
Model 6	97.35	9.15	0.20	0.17125
Model 7	93.73	0.80	0.20	0.17069
Model 8	83.46	0.46	0.20	0.15359
Model 9	96.96	0.34	0.10	0.10931
Model 10	94.71	0.80	1.18	0.09519
Model 11	90.29	1.04	0.69	0.03466
Model 12	95.39	0.23	0.10	-
Table 2B: TRPV1
Model	Rama Favored (%)	Rotamer outliers (%)	Rama outliers (%)	Mutual Info.
Model 1	81.20	0.37	0.16	-
Model 2	93.06	4.17	0.16	-
Model 3	91.96	0.23	1.65	0.055
Model 4	92.30	3.47	3.37	0.057
Model 5	90.94	1.62	0.17	0.059
Model 6	89.94	0.23	0.00	0.058
Model 7	94.28	26.57	0.00	0.053
Model 8	49.84	0.00	20.13	0.052
Model 9	53.67	0.69	18.53	0.049
Model 10	53.99	0.35	20.13	0.032
Model 11	57.51	0.69	16.61	0.008
Model 12	55.27	0.35	13.74	0.07
Model 13	58.15	1.39	15.97	0.07
Model 14	48.56	0.00	22.68	0.07
Model 15	53.67	0.35	20.77	0.07
Model 16	52.40	0.35	18.85	0.07
Model 17	91.51	0.20	0.35	0.07
Model 18	49.20	0.69	23.32	0.07

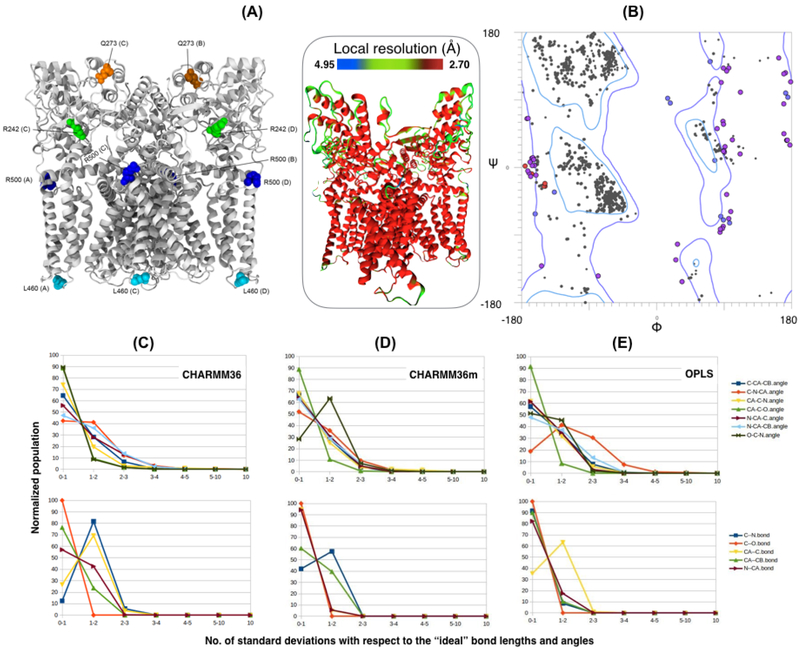
Worth noting is that higher Ramachandran-favored backbone statistics is often observed at the cost of unfavorable side chain rotamers. Extreme examples are observed for TRPV1, where a score of 94% Ramachandran-favored backbone statistics is obtained at the cost of 26% rotamer outliers (Table 2B - Model 7), and similarly in β-galactosidase 97% of Ramachandran-favored backbone statistics for 9% rotamer outliers (Table 2A - Model 6). For this specific criterion, ReMDFF models furnish 3-4% outliers, arguably on the poorer end of rotamer statistics determined from the complete models (incomplete models, though presented in the table, are not considered in this comparison). Presented in Figure 3, the Ramachandran deviations in ReMDFF are systematic, on the loops or non-repetitive regions of the model. The local resolution of the map is also lower in these areas, affecting high-quality refinement (Figure 3A (inset)). In view of this deficiency, ReMDFF results will be revisited below in the Results: Parameter dependence section to seek further improvements through better force fields.

Fig. 3. Detailed analysis ReMDFF-generated model geometry and force-field dependence.

(A) Structure of the TRPV1 model indicating location of major Ramachandran outliers. These residues, circled red on the Ramachandran diagram in (B), are found primarily in loop regions of the structure. (Inset) The TRPV1 structure colored by local resolution, computed using Resmap (Kucukelbir et al., 2014); residues featuring the Ramachandran outliers belong to the lower-resolution regions. (C-E) Normalized populations of bond-angle (upper pannels) and -length values (lower panel) observed cumulatively in ReMDFF models of β-galactosidase and TRPV1 plotted within standard-deviation bins with respect to ”ideal” geometries. A significant population of geometries are found in the second standard-deviation bin for for three different force fields - CHARMM36, CHARMM36m, and OPLS.

EMRinger score Third, EMRinger statistics are reported to judge simultaneously the quality-of-model as well as quality-of-fit of a structure, embodying a measure that combines the aforementioned CC and MolProbity scores. Described in reference (Barad et al., 2015), EMRinger provides a side-chain-directed approach to study model-to-map agreement. A higher EMRinger score is testament to more stereochemically plausible backbone geometries, monitored in terms of C_β and C_γ orientations within the density.

Illustrated in Figure 2I, the TRPV1 structures form two clusters characterizing the EMRinger values. Our ReMDFF model contribute to the lower edge of the upper cluster, in agreement with the fact that even though its CC-scores are high (Figure 2F - red circle), 3.47% sidechain outliers are still present (Table 2B Model 4). Indeed, structures with smaller sidechain outliers display higher EMRinger statistics. Table 2B - TRPV1 Models 3 and 5 feature lower outliers than the ReMDFF model (Model 4), and consequently, furnish higher EMRinger scores (Figure 2I - point no. 3 and 5).

For β-galactosidase, the mean EMRinger score for all the submitted models is higher than that for TRPV1. Here, benefiting from the better map resolution, ReMDFF yields a model with one of the highest EMRinger scores, 4.21. Thus, with a higher quality map ReMDFF delivers structures of better backbone and side chain geometries. This EMRinger comparison demonstrates the vantage point that ReMDFF is capable of accurately resolving 3-5 Å maps, which was considered a limitation of traditional MDFF (DiMaio et al., 2015).

Similarity to target model Closeness between the submitted and the target model is defined in terms of three metrics - RMSD of the heavy atoms with respect to the target model; CA-score, defined as the number of C_α atoms within 3 Å of the target model divided by RMSD with respect to the target; and mutual information between the model and target map measuring the so-called entropy of mixing between these two maps at a per-voxel level (Maes et al., 2003). EMDB submissions from the corresponding map are considered targets (PDBID: 3J7H for β- galactosidase, and 3J5P for TRPV1) (Bartesaghi et al., 2014, Liao et al., 2013).

Our ReMDFF model for β-galactosidase has the lowest RMSD with respect to the target, 0.6 Å, yet its statistics are much improved (Figure 2 & Table 2). Similarly for TRPV1 the RMSD from the target is quite small 1.23 Å noting that the data uncertainty is at least 3.4 Å. The CA-score and mutual information metric for β-galactosidase reflects a similar trend as RMSD, placing the ReMDFF model very close to the target. In contrast, for TRPV1, the CA-score is stratified into three clusters (Figure SI 1). ReMDFF features in the middle cluster with majority of the other complete models; the lower cluster includes all the incomplete models. Notwithstanding this intermediate range CA-score relative to other submissions, the structural statistics of the ReMDFF model for TRPV1, including EMRinger scores, are more refined than ones from the target.

A comparison of the submitted models with the target model remains incomplete without discussing the features of the target itself. In addition to the target’s structural quality, which is already mentioned above, here we employ root mean square fluctuations (RMSFs) for measuring plausible uncertainties in the target model borne out of the local resolution of the target map. The RMSF value quantifies deviation of the target model from the rest of the ensemble of structures representative of the same map (Singharoy et al., 2016). Depicted in Figure SI 2, RMSF of the target model increases in areas of the map where the local resolution is lower, implying a broader ensemble of structures being representative of the same data. A comparison between the β-galactosidase and TRPV1 targets reveals that the latter manifests higher RMSF values in the local resolution range of 3 to 4 Å suggestive of a broader ensemble of structures representing the same map. In agreement with this analysis a much larger variation is observed in the competition structures for TRPV1 than for β-galactosidase. Thus, we note that the TRPV1 target is less reproducible, bearing more uncertainty than β-galactosidase. In view of this analysis, determination of a submitted model’s quality through its comparison with the target model is a lot less informative with the TRPV1 target than with the β-galactosidase target.

Taken together, results from the 2015-2016 Cryo EM Model Challenge clearly demonstrate that ReMDFF delivers structures with map-fitting, backbone and sidechain geometry scores in the top-tier of all the entries. Model quality improves with map resolution, but the sidechain rotamer outliers can be further reduced. Leveraging this scope of further improvement, investigations are extended in the next section to optimize the ReMDFF refinement parameters.

Parameter dependence of ReMDFF models

In this section, we investigate the impact of three key flexible-fitting parameters on the ReMDFF results. Identification of these parameter dependencies in ReMDFF enables further improvement in our submitted models, and the formulation of some good practices in the use of MD simulation tools with EM maps (Discussion).

Force field parameters. Three different force field parameters were chosen to analyze their effects on ReMDFF results, namely CHARMM36 (already employed in the submitted competition models) (Best et al., 2012), CHARMM36m (a new version of CHARMM made available recently (Huang et al., 2017), providing more accurate estimation of backbone and side chain geometries than CHARMM36 in non-secondary-structure regions), and OPLS (a popular force field for in-liquid simulation of proteins) (Robertson et al., 2015). There is a clear dependence of ReMDFF results on the choice of force fields, and CHARMM36m provides the best results in terms of improving the molecular geometry further without compromising the global fitting attributes (Table 1A-B). Notably, benefitting from CHARMM36m, our competition structures are now further refined. For β-galactosidase, the Ramachandran-favored dihedral angles have now increased to 96.45% and bad angles came down to 0.73%. Overcoming the trend observed in most competition-structures, where the backbone improvements came at cost of marginally increasing the rotamer outliers (Table 2A), now, favored rotamers also increase (Table 1A). Similarly, for TRPV1, both the backbone and sidechain quality improved with the use of CHARMM36m force field, as indicated by a reduced number of Ramachandran and rotamer outliers over our CHARMM36 results (Table 2B). Consequently, the application of CHARMM36m in ReMDFF either retained or improved the EMRinger scores of the models.

A covalent bond geometry validation with the was performed using mmtbx.mp_geo (Adams et al., 2010). An output from this validation is the number of standard deviations, or sigmas, each bond or angle falls from the “ideal” value as stored in the .cif files of Phenix’s chem_data repository. Presented in Figure 3C-E, the geometries for β-galactosidase and TRPV1 feature significant population in the 1-2 sigma bin for the C–N peptide bond and the CA–C bond, as well as elevated N–CA bond and C-N-CA angle levels. This effect is irrespective of force fields used, but with OPLS exhibiting maximum deviation. The deviations are expected to originate from differences in the definitions of “ideal” bond or angle values between dictionaries in Phenix versus those in the classical force fields. However, all the force field-derived bond and angle geometries remain within the 4 sigma limit, implying they are accurate yet marginally shifted. In well-packed interiors, rotamer outliers occur at a quite low but genuine rate, stabilized either by positive interactions (e.g. 2–3 Hydrogen bonds) or by negative interactions (e.g. unusually tight packing). The empirical data used for MolProbity’s rotamer statistics constitute an approximate Boltzmann distribution. High-mobility or surface locations do not justify rotamer or C_β outliers, because in such regions there are fewer interactions that could hold a sidechain in an energetically unfavorable conformation. Thus, much more probable is an ensemble of good rotamers, which current techniques can justifiably model.

We note that the systematic error observed in ReMDFF model-quality at relatively unstructured regions of the system (Figure 3A-B) is partially remedied by CHARMM36m force fields. Further improvement is expected to be gained from a more robust definition of secondary-structure restraints, such as through the CaBLAM secondary-structure assignments that perform much better in the interpretation of 2.5 to 4 Å models than traditional DSSP or Ramachandran criteria because they depend on C_α-trace geometry rather than on peptide orientation (Williams et al., 2018). Work is currently in progress towards this CaBLAM use in MDFF, which would not prevent or affect the use of CaBLAM outliers for model validation.

A lack of an explicit simulation environment such as water, ions or membrane in ReMDFF refinements explains the lower-quality structures from OPLS, which is meant for liquid simulations with MD. Furthermore, OPLS is known to overestimate protein flexibility, which also facilitates sampling of Ramachandran-unfavored conformations (Trbovic et al., 2008). Even though flexible-fitting benefits from the inclusion of explicit environments (Qi et al., 2017), explained in the next subsection, a combination of CHARMM36m with implicit solvent conditions provides similar results at much lesser computational expenditure.

Choice of initial model ReMDFF is biased to the choice of initial models. At present, it cannot refine the secondary-structure folds of an initial model. However, as showcased here and in our previous studies (Singharoy et al., 2016, Schweitzer et al., 2016, Wehmer et al., 2017), ReMDFF can refine backbone and side chain statistics of the initial model depending upon the cogent use of force field parameters. We test now an initial model of much poorer quality than the reported targets for β-galactosidase. As reported in reference (Singharoy et al., 2016), this model is prepared by an initial annealing protocol (See Section in SI) that reduces the secondary-structure quality and the initial fit. Presented in SI Table 1, ReMDFF simulations with CHARMM36m force fields successfully resurrected this model. Backbone RMSD relative to the competition target changed from 7 Å to 0.9 Å after the ReMDFF refinement, showcasing the capability of this method in capturing large-scale deformations. The most significant is improvements in side chain placement where rotamer outliers decreased from around 6% to 2% and C_β deviations also came down from 8.6% to 0.5%, a result almost robust to the choice of the map-model coupling parameter ζ in Eq. 1. Therefore, ReMDFF can improve the geometries of meaningful yet low-quality models, often found in ab initio modeling (Terwilliger et al., 2018). Nonetheless, a better quality initial model almost always yields more dependable final results. When experimentally reported structures were employed as the initial model (Table 1) quality of the ReMDFF refinements are better than those starting from an artificially annealed model (SI Table 1).

Map-Model coupling parameters. Presented in SI Table 1, the ReMDFF results for β-galactosidase depend minimally on the choice of ζ (GSCALE parameter in NAMD), at least within the range of chosen values. Nonetheless, for a value of 0.4 the overall MolProbity score is minimum implying a model simultaneously satisfying most of the geometry criteria. Distortion of the structure is expected in higher GSCALE values (McGreevy et al., 2016, Monroe et al., 2017). Additionally, we note that a more compute-expensive explicit solvent ReMDFF only minimally changes the result from implicit solvent computations (SI Table.1). Such expensive computations indeed assisted the fitting of large domains in traditional MDFF with low-resolution density maps (Hsin et al., 2010), but our new resolution-exchange protocol together with CHARMM36m force fields, provide comparable results with much more computationally tractable implicit-solvent, namely Generalized Born model (Still et al., 1990, Onufriev et al., 2004). However, since solvent dependencies of MD simulations are often non-trivial, it remains a good practice to re-refine the best implicit-solvent ReMDFF model in explicit solvent (Qi et al., 2017), if resources permit.

Discussion

Experience from the Cryo-EM Challenge allows us now to formulate a prescription for ReMDFF usage, particularly for the so called high-resolution maps in the 3 - 5 Å regime. First, ReMDFF is a preferable choice for flexible-fitting over traditional MDFF, overcoming clear limitations of the latter (Singharoy et al., 2016). Second, CHARMM36m is the preferred force field over older versions of CHARMM and OPLS; in the absence of any test, we abstain from commenting on AMBER force field (Cornell et al., 1995). Though we note, AMBER minimization-based (not MD-based) refinements have been performed with density data, and ReMDFF is compatible with AMBER force fields in NAMD, enabling a similar task. Third, the GSCALE values designated in the NAMD configuration files should range from 0.3 to 0.6. A search of the best parameter is required nonetheless for the problem of interest. Fourth, an increment of 0.5 Å in the half-width of Gaussian blurs is found adequate during ReMDFF. For the competition models above, and in ongoing studies, we have tested up to 11 blurred maps to perform resolution exchange with Gaussian half-widths ranging from 0.5 Å to 5.5 Å. If needed this number of blurred maps can be increased, e.g. when topology information in the initial model is poor, but we suggest an initial test with at least 11 maps. To this end, the use of MDFF-GUI (McGreevy et al., 2016) on VMD1.9.4 onward allows automatic generation of an arbitrary number of blurred maps and ReMDFF input files. For the generation of MDFF input files with more expensive explicit solvent or membrane environments, a CHARMMGUI-MDFF web interface is now available (Qi et al., 2017). Finally, along with necessary scores reported in this article, we recommend an ReMDFF model should be reported with an evaluation of local RMSF and source of initial model. An RMSF-evaluation provides quantitatively the uncertainty in ReMDFF modeling, and the more uncertain regions, if need be, can be treated separately with available rotamer libraries. To this end, the RMSF computations of the converged ReMDFF trajectory can be performed on VMD employing the Timeline tool. A comparison with the initial model quantifies model-bias in the ReMDFF output, some unfixable errors in which can be due to the initial model itself and not the application of the best force fields. Such errors can be fixed employing the Cispeptide and TorsionPlot plugins on VMD (McGreevy et al., 2016).

Conclusions

Altogether, the current investigation is an attempt to evaluate the advantages and shortcomings of a real-space fitting method based on the best available classical force fields, and in the hand of well-trained users. Surprisingly, we find that the results are more dependent on default refinement parameters such as map-resolution and force field, rather than user-choice parameters such as GSCALE. For the first time, ReMDFF results are compared across multiple force fields. Our results are compared against all available models from the Cryo-EM challenge, consistently placing ReMDFF within the top scores across several cross-validation methodologies. However, the choice of initial model quality remains a key user decision. To this end, ReMDFF can significantly improve the quality of an initial model as long as the overall topology remains correct in these models. Finally, a set of good-practices is formulated that assists reproducibility of MDFF results, and more importantly, allows non-experts to set-up and benefit from MD-based molecular refinements.