Skip to main content
. 2019 Feb 28;8:e41535. doi: 10.7554/eLife.41535

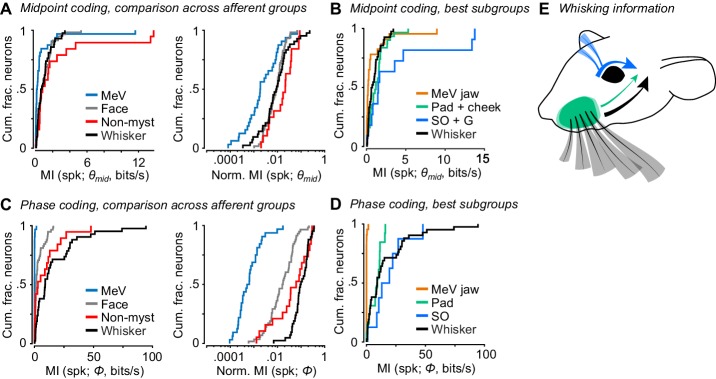
Figure 6. Coding of self-motion by diverse classes of facial mechanoreceptors.

(A) Left, summary cumulative histograms of MI rate between spike count and θmid for whisking-sensitive MeV (n = 33), face (n = 58), non-mystacial vibrissae (n = 19), and whisker units (n = 42). Right, summary histograms of normalized MI between spike count and θmid for same units. (B) Summary histograms of MI rate between spike count and θmid for the best encoding subgroups of whisking-sensitive units: putative jaw proprioceptors in MeV (n = 23), pad and cheek units (n = 31), supraorbital and genal units (n = 11), and whisker units (replotted from A). (C) Left, same as (A) but for MI rate between spike count and Φ. (D) Same as (B) but for the subgroups that best encoded Φ: putative proprioceptors in MeV (n = 23), pad units (n = 13), supraorbital units (n = 8), and whisker units (replotted from C). (E) Schematic depicting flow of information about whisking kinematics from various peripheral mechanoreceptors to the brain: whisker follicle (black), supraorbital vibrissa (blue), and whisker pad hairy skin (green) afferents. (B–D) Panels include data from Figures 2–5 plotted together for comparison. Data for panels A and C are given in Figure 6—source data 1. Data for panel B are given in Figure 6—source data 2. Data for panel D are given in Figure 6—source data 3.

Figure 6—source data 1. MATLAB R2016b ‘table’ data structure with MI and Normalized MI values shown in Figure 6A,C.
elife-41535-fig6-data1.mat (15.7KB, mat)
DOI: 10.7554/eLife.41535.028
Figure 6—source data 2. MATLAB R2016b ‘table’ data structure with MI values shown in Figure 6B.
elife-41535-fig6-data2.mat (2.4KB, mat)
DOI: 10.7554/eLife.41535.029
Figure 6—source data 3. MATLAB R2016b ‘table’ data structure with MI values shown in Figure 6D.
elife-41535-fig6-data3.mat (2.1KB, mat)
DOI: 10.7554/eLife.41535.030

Figure 6.

Figure 6—figure supplement 1. Alternative binning methods for mutual information calculation.

Figure 6—figure supplement 1.

(A) Joint distribution for spike count and Φ comparing binning of Φ with linear spacing (LS, left, same calculation reported throughout paper) and uniform count (UC, right) for an example unit. Marginal probability distributions are plotted for Φ (top) and spike count (right). Note that the LS distribution of Φ is nearly uniform, except fewer bins are observed during retraction phases due to more rapid whisker retraction. MI rate values calculated using each method of binning are reported at top. (B) Same as (A), but for spike count and θmidcomparing LS (left) and UC (right) for an example whisker afferent. (C) Cumulative histograms of MI rate between spike count and Φ, calculated using LS (solid lines) or UC (dotted lines) for the different afferent groups. (D) Same as (C) but for MI rate between spike count and θmid. (E) Same as (C) but for best subgroups. (F) Same as (D) but for best subgroups. (C-F) LS values are repeated from Figure 6 to allow comparison with UC values. For Φ and θmid, MI values calculated with LS or UC binning are almost identical.
Figure 6—figure supplement 2. Confidence intervals for mutual information and dependence on sample size.

Figure 6—figure supplement 2.

(A) MI rate (± 95% bootstrap CI) between spike count and Φ for all whisking-sensitive units (n = 152). Cyan: results of same calculation but after randomly shuffling spike counts with respect to Φ. Neurons are sorted by group label (right) and MI rate. (B) Mean number of frames in each bin (n = 16 bins) for marginal distribution of Φ, plotted against the width of the 95% CI for MI rate for Φ. Cyan: results of same calculation after randomly shuffling spike times with respect to Φ. (C) Cumulative histogram showing mean number of frames per bin for all whisking-sensitive units (n = 152). (D) Same as (A), but with MI rate calculated between spike count and θmid. (E) Same as (B), but for θmid. (A,D) MeV data are repeated from Figure 5E.
Figure 6—figure supplement 3. Mutual information calculated using varying windows for spike count.

Figure 6—figure supplement 3.

(A) MI values for spike count and Φ calculated using different spike count window durations, ranging from 1 to 64 ms for all whisking-sensitive units (rows). Values are normalized from min to max MI across time windows for each unit. Rows are sorted by afferent group (labels on right) and within group by index of max. (B) Mean MI values (± SEM) for spike count and Φ, for each afferent group and spike count window, after normalizing each unit as in (A). (C) Summary cumulative histograms of MI rate between spike count and Φ for all whisking-sensitive MeV, face, non-mystacial vibrissae, and whisker units, for 2 ms (solid lines, taken from Figure 6C) and 8 ms (dashed lines) windows. (D–F) Same as (A-C) but for θmid (2 ms window data taken from Figure 6A). (G) MI rates between spike count and Φ, calculated for varying spike time shifts relative to Φ, in 0.5 ms increments for all whisking-sensitive units (rows). Conventions as in (A). (H) Same as (B) but for spike time shifts.