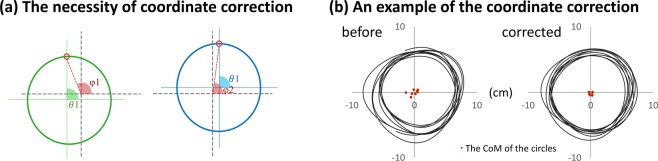
Figure 4.

Coordinate correction. (a) The necessity of coordinate correction before calculating the phase values. From the Center of Mass (CoM) of the left (green) and right (blue) circles, the two small red dots both lie on 90 degrees of the circles (θ1 = θ2). However, when the two circles are lying on a common coordinate (black coordinate) with a spatial shift, the phase value of the two dots become different ($\varphi 1\ne \varphi 2$). (b) An example of coordinate correction. The participant had slight movement of the CoM between each cycle. After correction, the CoM between cycles becomes more stable. The tiny red dots represent the CoM of each circle.