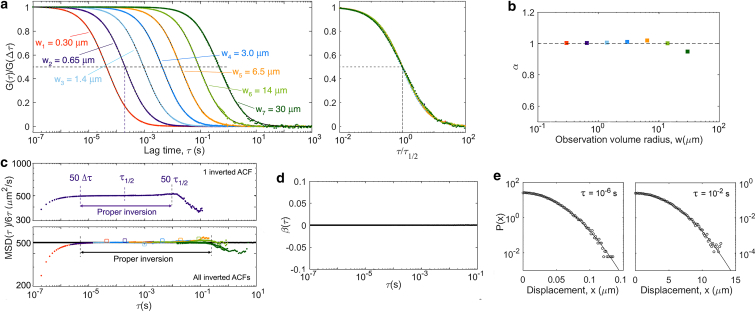
Figure 4.

Results of the VLS-FCS simulations for simple diffusion (D = 500 μm/s²). (a) ACFs obtained for different observation volume sizes are shown (colored symbols: simulations; black lines: fit of Eq. 15 to the simulated data—the fit is behind the data and difficult to see except for the largest detection volumes). The same ACFs, with lag time normalized by τ_1/2, are shown in the right panel. Their perfect superposition is a reflection of the self-similarity of the process. (b) The apparent anomalous exponent obtained from the fit of the ACFs in (a) is shown. The dashed line is a guide for the eye showing the expected α = 1 value for simple diffusion. (c) Upper panel: apparent diffusion coefficient, $\langle {\tilde{r}}^2\rangle /\left(6\tau \right)$, calculated from the inversion of a single ACF (w₂ = 0.65 μm), which has the expected constant value for several decades in time around τ_1/2. Lower panel: apparent diffusion coefficient calculated from the inversion of all the ACFs shown in (a) and compared to the actual diffusion coefficient, $\langle r^2\rangle /\left(6\tau \right)$, obtained directly from the particle trajectories (black line). Empty symbols show the diffusion law (i.e., the value of w²/(4τ_1/2) as a function of τ_1/2 for each ACF). (d) The non-Gaussian parameter calculated from the trajectories (black line) and expected β = 0 value for simple diffusion (dashed line) is shown. (e) Distributions of displacements for τ = 10⁻⁶s (left) and τ = 10⁻²s (right) are shown. Lines are fitted to a Gaussian distribution. To see this figure in color, go online.