Fig. 1.

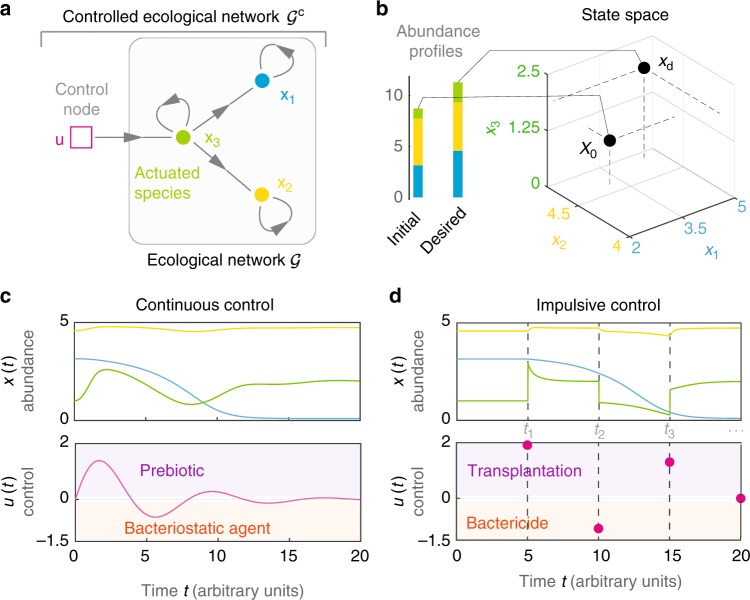
Controlling a microbial community. a Ecological network $\mathcal{G}$ for a toy microbial community of N = 3 species (green, yellow, blue). The controlled ecological network ${\mathcal{G}}^{\mathrm{c}}$ contains M = 1 control input actuating the third species. b Initial and desired abundance profiles (bars). Controlling the community consists in driving its state from the initial state x₀ to the desired state x_d, represented by two points in the state space of the community. c In the continuous control scheme, the control inputs u(t) are continuous signals modifying the growth of the actuated species. The controlled population dynamics of this community is given by ${\dot{x}}_1=0.1+x_1\left(1-x_1∕5\right)\left(x_1∕3-1\right)-\left(0.1x_1{x}_3\right)∕\left(1+x_3\right)$, ${\dot{x}}_2=0.1+x_2\left(1-x_2∕4\right)\left(x_2-1\right)+\left(x_2{x}_3\right)∕\left(1+x_3\right)$, ${\dot{x}}_3=x_3\left(1-x_3∕2\right)\left(x_3-1\right)+u$. In the absence of control, this community has two equilibria $x_0={\left(3.14,4.58,1\right)}^{\top }$ and $x_{\mathrm{d}}={\left(4.57,4.73,2\right)}^{\top }$, chosen as the initial and desired states, respectively. d In the impulsive control scheme, the control inputs u(t) are impulses applied at the intervention instants $\mathbb{T}=\left\{t_1,t_2,\cdots \right\}$, instantaneously changing the abundance of the actuated species. The controlled population dynamics is the same as in panel (c), except that ${\dot{x}}_3=x_3\left(1-x_3∕2\right)\left(x_3-1\right)$ and x₃(t⁺) = x₃(t) + u(t) if $t\in \mathbb{T}=\left\{5,10,15\right\}$. Under this controlled population dynamics, our mathematical formalism identifies x₃ as the solo driver species needed to drive this microbial community (Example 1 in Supplementary Note 2)