The Evolution of Small-RNA-Mediated Silencing of an Invading Transposable Element

Abstract

Transposable elements (TEs) are genomic parasites that impose fitness costs on their hosts by producing deleterious mutations and disrupting gametogenesis. Host genomes avoid these costs by regulating TE activity, particularly in germline cells where new insertions are heritable and TEs are exceptionally active. However, the capacity of different TE-associated fitness costs to select for repression in the host, and the role of selection in the evolution of TE regulation more generally remain controversial. In this study, we use forward, individual-based simulations to examine the evolution of small-RNA-mediated TE regulation, a conserved mechanism for TE repression that is employed by both prokaryotes and eukaryotes. To design and parameterize a biologically realistic model, we drew on an extensive survey of empirical studies of the transposition and regulation of P-element DNA transposons in Drosophila melanogaster. We observed that even under conservative assumptions, where small-RNA-mediated regulation reduces transposition only, repression evolves rapidly and adaptively after the genome is invaded by a new TE in simulated populations. We further show that the spread of repressor alleles through simulated populations is greatly enhanced by two additional TE-imposed fitness costs: dysgenic sterility and ectopic recombination. Finally, we demonstrate that the adaptive mutation rate to repression is a critical parameter that influences both the evolutionary trajectory of host repression and the associated proliferation of TEs after invasion in simulated populations. Our findings suggest that adaptive evolution of TE regulation may be stronger and more prevalent than previously appreciated, and provide a framework for interpreting empirical data.

Introduction

Transposable elements (TEs) are intragenomic parasites. Although some TE families or individual TE insertions have been âdomesticatedâ to perform important functions (Kunarso etÂal. 2010; Lynch etÂal. 2011; Silva-Sousa etÂal. 2012), their presence and mobilization generally reduce the fitness of their host. TEs introduce deleterious mutations by causing DNA damage during mobilization and by inserting into functional sequences (Spradling etÂal. 1999; Dupuy etÂal. 2001), or disrupting the expression of adjacent genes by inducing heterochromatin formation (Hollister and Gaut 2009; Sentmanat and Elgin 2012; Lee 2015; Lee and Karpen 2017). Ectopic recombination events between TE insertions in different genomic locations further produce large structural rearrangements, duplications, and deletions, which are overwhelmingly deleterious (reviewed in Hedges and Deininger 2007). In addition to these mutational impacts, TE activity itself can have drastic fitness consequences by causing dysgenic sterility, a condition in which germline DNA damage prohibits the production of viable gametes (Bingham etÂal. 1982; Josefsson etÂal. 2006; Orsi etÂal. 2010; Tasnim and Kelleher 2018). Despite these fitness costs, nearly all genomes are populated by TEs (reviewed in Huang etÂal. 2012), and TEs frequently colonize new genomes through horizontal transfer (reviewed in Schaack etÂal. 2010).

Host regulation of transposition is as ubiquitous as TEs themselves; both prokaryotic and eukaryotic genomes control TE activity through small-RNA-mediated silencing pathways (reviewed in Blumenstiel 2011). In eukaryotic germlines, small-RNA-mediated silencing of TEs is enacted by complexes of Argonaute proteins and small-interfering RNAs (siRNAs) or Piwi-interacting RNAs (piRNAs). The siRNAs and piRNAs are produced from antisense TE transcripts and identify TE-derived mRNAs by base complementarity. Argonaute proteins then silence target TEs transcriptionally or posttranscriptionally. Consistent with prevention of germline DNA damage, small-RNA-mediated silencing suppresses TE-associated dysgenic sterility in Drosophila (Blumenstiel and Hartl 2005; Brennecke etÂal. 2008; Chambeyron etÂal. 2008; Rozhkov etÂal. 2010) and Arabidopsis (Josefsson etÂal. 2006). Transcriptional silencing may further reduce the rate of ectopic recombination between TE insertions by inducing heterochromatin formation at TE loci (Haynes etÂal. 2006; Sentmanat and Elgin 2012; Sienski etÂal. 2012).

Although the mechanism of small-RNA-mediated silencing has been investigated extensively, we know very little about how it evolves when a genome is invaded by a new TE. In part, this reflects an absence of opportunity, since, although ancient TE invasions are easily identified from comparative genomic data (reviewed in Schaack etÂal. 2010), ongoing invasions have only rarely been detected in extant populations (Kidwell 1983; Periquet etÂal. 1989; Evgenâev et al. 2000; Hill etÂal. 2016). Additionally, the adaptive evolution of transpositional repression is a long-standing theoretical challenge in sexually reproducing organisms. Prior to the discovery of small-RNA-mediated silencing, a series of classic analytical models suggested that positive selection on trans-acting transpositional repressors, such as small-RNA-encoding loci, was likely to be weak, because recombination would rapidly decouple repressor alleles from the chromosomal regions that they protect from TE-induced mutation load (Charlesworth and Langley 1986). Restrictive conditions for the adaptive evolution of repressor alleles are difficult to reconcile with the prevalence of small-RNA-mediated TE silencing across the tree of life.

When a genome is invaded by a new TE, small-RNA-mediated silencing is thought to evolve by transposition of the invading TE into a small-RNA-producing site, thereby initiating the production of new RNA species that target the invading element for silencing (Brennecke etÂal. 2008; Khurana etÂal. 2011). TE insertions in small-RNA-producing sites therefore represent a class of repressor alleles that arise via de novo mutation during an invasion event. Using forward simulations of retrotransposon invasion into a Drosophila melanogaster-like genome, Lu and Clark (2010) demonstrated that small-RNA-producing insertions are targets of positive selection and made a general case for adaptive evolution of small-RNA-mediated TE silencing. However, because their model is not based on any particular TE family, it is unclear how accurately the results reflect an actual invasion event. Additionally, Lu and Clark (2010) did not explicitly consider dysgenic sterility or ectopic recombination, two major TE-imposed fitness costs that could enhance positive selection on repressor alleles.

Here, we draw on an extensive body of literature on P-element DNA transposons and their recent invasion into natural populations of D. melanogaster (reviewed in Kelleher 2016) to motivate a forward, individual-based simulation model of the evolution of small-RNA-mediated repression in response to a TE invasion event. By incorporating empirically estimated fitness costs, transposition rates, and effects of small-RNA-mediated silencing into our model, we generate simulated populations that recapitulate the key features of the P-element invasion, including both the spread of the TE through natural populations and the acquisition of repression by the host. We then interrogate the degree to which different TE-imposed fitness costs (i.e., deleterious mutations, dysgenic sterility, and ectopic recombination) enhance positive selection on repressor alleles in those simulated populations. Finally, we consider how the distinct genetic architecture of small-RNA-mediated TE silencingâin which many sites across the genome produce small RNAs when occupied by a TEâaffects the evolution of repression.

We demonstrate that small-RNA-mediated silencing of transposition alone evolves rapidly and adaptively in response to genome invasion in simulated populations. We further demonstrate that dysgenic sterility and ectopic recombination can greatly enhance the strength of positive selection on insertions in small-RNA-producing sites in simulated populations. Finally, we reveal that the abundance of small-RNA-producing sites in the host genome is a critical parameter that influences both the proliferation of the TE and the adaptive behavior of repressor alleles in simulated populations. Our study provides fundamental insights into selective forces that influence the evolution of repression, as well as an updated framework for modeling TE invasion.

Model

We employ an individual-based WrightâFisher model of evolution, with a selectionâreproductionâtransposition life cycle, constant population size, and discrete, nonoverlapping generations. See tableÂ1 for a list of parameters.

Table 1.

Model Variables and Parameters

	Description
E0	Baseline ectopic recombination rate (eq.Â5)
É	Fitness cost of ectopic recombination (eqs.Â2 and 5)
F	Fertility (eqs.Â2 and 4)
D	Maximum possible fertility cost caused by dysgenesis (eq.Â4)
$W_{\mathrm{â}}$	Male fitness (eq.Â2)
$W_{\mathrm{â}}$	Female fitness (eq.Â2)
N	Population size
n	Total number of TE insertions (eq.Â4)
na	Number of TE insertions in functional and neutral sites (eqs.Â1 and 5)
nm	Number of TE insertions in maternal genome (eq.Â6)
s	Effect of a TE insertion on viability (tableÂ2; eq.Â3)
R	Strength of small-RNA-mediated repression (eqs.Â1 and 4â6)
u	Transposition rate per genome per generation (eq.Â1)
Î	Transposition rate per element per generation (eq.Â1)
V	Viability (eqs.Â2 and 3)

Genome

The genome is modeled after that of D. melanogaster. Each individual is diploid with a haploid complement of three chromosomes: one sex chromosome containing 226 sites, and two autosomes containing 442 and 527 sites, respectively (total: 1,195 sites). The numbers of sites per chromosome are based on the lengths of D. melanogaster chromosomes X, 2 and 3, with one site every $â{10}^5$ base pairs (we ignore chromosome 4, which accounts for <1% of the genome). Likewise, the recombination rates at each chromosomal site are set to reflect the actual D. melanogaster recombination rates (Comeron etÂal. 2012).

Previous theoretical models of TE dynamics assume that TE insertions in all genomic sites are equally deleterious, and that they exhibit negative epistasis with respect to fitness (e.g., Dolgin and Charlesworth 2008; Lu and Clark 2010; Lee and Langley 2012). The latter assumption appears to be required for TE copy number to evolve to equilibrium in the absence of repression (Charlesworth B and Charlesworth D 1983). Although it has been proposed that the aneuploid progeny that result from ectopic recombination (Langley etÂal. 1988; Petrov etÂal. 2003, 2011), or copy-number dependent heterochromatin formation (Lee and Langley 2010; Lee 2015; Lee and Karpen 2017), could produce negative epistasis between TE insertions, the commonly used mathematical expression for negative epistasis (Charlesworth 1990) is based on the observed pattern of fitness decline in a mutation accumulation experiment on D. melanogaster (Mukai 1969). The extent to which the results of the Mukai (1969) experiment reflect the fitness consequences of TEs or interactions between TE insertions of the same family is unknown.

Here, we take a different approach, by considering a more complex and realistic genome in which the fitness effects of TE insertions vary between sites. We furthermore drew extensively on empirical data to determine composition of the genome and the distribution of fitness effects for insertions into individual sites. The genome contains four kinds of sites: small-RNA sites, pseudo-small-RNA sites, functional sites and neutral sites, which differ in their effects on viability, their participation in transposition and ectopic recombination, and their role in small-RNA-mediated silencing. The properties of each type of site are described below.

Functional Sites

Functional sites cause a multiplicative change in viability (eq.Â3)âand, therefore, fitness (eq.Â2)âwhen occupied by a TE. Thus, there is no epistasis for viability. We furthermore assume that the effects on viability of TE insertions in functional sites are completely recessive, as has been observed empirically for P-elements (Mackay etÂal. 1992). To determine the number of functional sites in our theoretical genome, we relied on results from extensive P-element-mediated mutagenesis screens, which indicate that $â80\%$ of new P-element insertions occur in gene bodies, within 500âbp of a transcription start site (Bellen etÂal. 2004, 2011). Accordingly, 80% (956) of sites in our theoretical genome are functional (tableÂ2) and affect viability when homozygous for a TE insertion.

Table 2.

Viability Selection Coefficients (s), and Contribution to Transposition (T), Dysgenic Sterility (D), Ectopic Recombination (E), and Repression of Transposition (R) of TE Insertions in the 1,195 Sites of Different Kinds

Type	T	D	E	R	s	Sites	Frequency (%)
Â	Â	Â	Â	Â	Â	Â	Â
Functional
$\text{â}$Lethal	Yes	Yesa	Yesa	No	â1.00	45	3.8
$\text{â}$Strongly deleterious	Yes	Yesa	Yesa	No	â0.25	325	27.2
$\text{â}$Moderately deleterious	Yes	Yesa	Yesa	No	â0.05	350	29.3
$\text{â}$Slightly deleterious	Yes	Yesa	Yesa	No	â0.01	224	18.7
$\text{â}$Slightly beneficial	Yes	Yesa	Yesa	No	+0.01	12	1.0
Neutral	Yes	Yesa	Yesa	No	0.00	169	14.1
Small RNA	No	Yesa	No	Yes	0.00	35	2.9
Pseudo-small RNA	No	Yesa	No	No	0.00	35	2.9

^aIn some simulations.

Neutral Sites

A total of, 169 neutral sites (14.1% of sites in the genome) have no effect on viability when occupied by a TE. However, TE insertions in neutral sites, like those in functional sites, contribute to both dysgenic sterility and the production of inviable gametes through ectopic recombination in some simulations (see Dysgenic Sterility and Ectopic Recombination).

Small-RNA Sites

A total of 35 sites (2.9% of sites in the genome) establish small-RNA silencing when occupied by a TE, and represent the piRNA producing regions in the D. melanogaster genome known as piRNA clusters (Brennecke etÂal. 2007). The locations of small-RNA sites are randomly drawn from the known locations of piRNA clusters in the D. melanogaster genome (Brennecke etÂal. 2007). The location of small-RNA sites is the same in all simulations, except when the genomic fraction of small-RNA sites is varied. Because piRNA clusters are generally found in heterochromatic regions where chromatin compaction restricts transposition and recombination (Brennecke etÂal. 2007), TE insertions in small-RNA sites do not transpose and do not participate in ectopic recombination in our model. However, TE insertions in small-RNA sites do contribute to dysgenic sterility in some simulations (see Dysgenic Sterility).

Pseudo-Small-RNA Sites

A total of 35 sites (2.9% of sites in the genome) do not contribute to small-RNA silencing but are otherwise indistinguishable from small-RNA sites. Biologically, they represent transcriptionally quiescent heterochromatic sites where ectopic recombination is unlikely. They also provide a neutral site class against which to evaluate the frequency spectra of small-RNA sites. Pseudo-small-RNA sites are placed near telomeres or centromeres, which mirrors the distribution of piRNA clusters in the D. melanogaster genome. Each chromosome arm contains three and four pseudo-small-RNA sites at the proximal and distal ends, respectively, skipping sites that are already assigned as either small RNA or functional.

Transposition, Excision, and Inactivation

The transposition rate per genome per generation is given by

$$u=Îî¼n_{\mathrm{a}}\left(\frac{kâR}{k}\right)\text{â},$$ (1)

where Î is the transposition rate per element per generation of unrepressed TEs, n_a is the number of TEs in the genome that can be mobilized in the presence of transposase (i.e., those in functional and neutral sites, but not in small-RNA or pseudo-small-RNA sites), R is the strength of small-RNA-mediated repression (see eq.Â6), and k is a constant. We consider $Î=0.1$ and $Î=0.01$ according to the range of empirical estimates for unregulated transposition of P-elements (Eggleston etÂal. 1988; Robertson etÂal. 1988; Berg and Spradling 1991; Kimura and Kidwell 1994). We also set kâ=â1.01, in order to limit the reduction in transposition rate caused by small-RNA-mediated silencing to 2 orders of magnitude, as is suggested by observed differences in P-element activity in the presence and absence of regulation (Eggleston etÂal. 1988).

Although P-elements are DNA transposons, precise excisions are rare, because the excised copy is often restored to the excision site via homologous repair (Engels etÂal. 1990). Precise P-element excisions occur during transposition, with an estimated frequency of 0.15% (per element per genome transposition event) when the insertion is homozygous, and $â13.5\%$ when the insertion is heterozygous (Engels etÂal. 1990). We therefore assume that the excision rate is 10% of the transposition rate. Mutational loss of transposase-encoding capacity, which occurs predominantly through internal deletions that are acquired during transposition (Staveley etÂal. 1995), occurs at a rate of $0.01Î$ per element per generation.

Fitness

Male and female fitness are given by

$$W_{\mathrm{â}}=VF\text{âandâ}{W}_{\mathrm{â}}=VF\text{â}(1âÎ),$$ (2)

respectively, where

$$V=\underset{i}{â}(1+s_i)\text{â}$$ (3)

is viability, s_i is the viability selection coefficient of the TE insertion into the ith locus in a hemizygous or homozygous state, F is fertility (eq.Â4), and É is the fitness cost of ectopic recombination (eq.Â5).

Viability

When homozygous, the effect on viability of a TE insertion at a functional site can be lethal (selection coefficient, s = â1), strongly deleterious $(s=â0.25)$, moderately deleterious $(s=â0.05)$, slightly deleterious $(s=â0.01)$, or slightly beneficial $(s=+0.01)$. The frequency of each functional site class in the theoretical genome is described in tableÂ2 and is based on the empirically estimated distribution of fitness effects of individual P-element insertions (Cooley etÂal. 1988; Mackay etÂal. 1992; Lyman etÂal. 1996). Specifically, P-element mutagenesis revealed that the frequency of recessive lethal mutations produced by individual insertions is in the range 3.8â10% (Cooley etÂal. 1988; Mackay etÂal. 1992). Therefore, we conservatively assigned 3.8% of sites in the theoretical genome to behave as recessive lethals when occupied by a TE. Similarly, the average homozygous viability fitness effect of a TE insertion in the theoretical genome, $\stackrel{Â}{s}=â12.2\%$, matches a quantitative estimate from a series of P-element insertion lines (Mackay etÂal. 1992). We refer to this empirically estimated viability fitness model as Ï_e. In a subset of simulations, we reduce these fitness effects 10-fold, in order to explore the degree to which the magnitude of viability fitness costs influences invasion dynamics. We refer to this reduced effects viability fitness model as Ï_r.

Dysgenic Sterility

When Drosophila males bearing a transpositionally active TE family are crossed to females who do not produce a sufficient abundance of piRNAs that regulate that TE family, their F1 offspring can suffer from dysgenic sterility (Bingham etÂal. 1982; Bucheton etÂal. 1984; Blackman etÂal. 1987; Yannopoulos etÂal. 1987; Evgenâev et al. 1997; Brennecke etÂal. 2008; Hill etÂal. 2016). We therefore modeled dysgenic sterility as a function of the number of genomic TEs, whose unregulated activity is thought to induce the sterility phenotype (eq.Â4). Indeed, in the case of P-element-induced dysgenic sterility, the proportion of offspring that are sterile has been correlated with the P-element germline excision rate, consistent with P-element activity as the cause of sterility (Kocur etÂal. 1986). Dysgenic sterility is further modified in our model by the production of small RNAs in the maternal genotype (R).

Dysgenic sterility occurs in both sexes, although it is most extensively studied in females, in whom it tends to be more severe (Kidwell etÂal. 1977). In particular, Bingham etÂal. (1982) described the quantitative relationship between the number of paternally inherited P-elements and the incidence of dysgenic sterility among F1 female offspring. The paternal genotypes that induced dysgenesis in these crosses were otherwise isogenic, such that differences in dysgenic sterility among F1 females could be exclusively attributed to P-element copy number. They observed that nâ=â4âP-element copies produced $â50\%$ dysgenic offspring, whereas $nâ9$ copies produced $â80\%$ dysgenic offspring. There were very limited data on induction by paternal strains containing nâ<â4âP-element copies.

We matched these empirical observations by expressing the fertility, F, of an individual as a function of its total diploid TE copy number (n). In contrast to viability fitness therefore, where the fitness effects of individual insertions are recessive within loci, and additive across loci, each P-element insertion contributes epistatically to the fitness cost of ectopic recombination, regardless of whether it is found in a homozygous or heterozygous state. Fertility is given by

$$F=\text{Â}\{\begin{array}{cc}1âDî¼(1âR)\left(\frac{nâ3}{nâ2}\right)â,\hfill & â\text{if}âânâ4\hfill \\ 1â,\hfill & â\text{otherwise}â,\hfill \end{array}$$ (4)

where D is a constant that represents the maximum fertility cost, and can be varied from 0 (no dysgenic sterility) to 1 (complete dysgenic sterility) and R is the strength of small-RNA-mediated repression in the maternal genotype (see eq.Â6). F can vary from 0 (complete infertility) to 1 (complete fertility).

Ectopic Recombination

Ectopic recombination occurs between TE insertions in different genomic sites, and produces inviable gametes in our model. We assume that the fitness cost of ectopic recombination is proportional to the number of pairwise combinations of TEs in the genome, excluding insertions in small-RNA and pseudo-small-RNA sites. The fitness consequences of ectopic recombination are, therefore, analogous to the negative epistasis between TE insertions that is assumed by previous models (Dolgin and Charlesworth 2006, 2008; Lu and Clark 2010; Lee and Langley 2012). Each P-element insertion contributes epistatically to the fitness cost of ectopic recombination, regardless of whether it is found in a homozygous or heterozygous state.

Small-RNA-mediated silencing acts as a multiplicative modifier of ectopic recombination, which reflects the potential suppression of recombination at TE loci due to heterochromatin formation (Haynes etÂal. 2006; Klenov etÂal. 2007). The fitness cost of ectopic recombination $(É)$ is described by the following expression:

$$É=n_a(n_aâ1)(1âR)E_0,$$ (5)

where E₀ is the baseline ectopic recombination rate; n_a is the number of TE insertions that can contribute to ectopic recombination (i.e., do not occur in small-RNA or pseudo-small-RNA sites); and R is the strength of small-RNA-mediated repression.

Small-RNA-Mediated Silencing

piRNA-mediated silencing represses both germline TE activity and dysgenic sterility in Drosophila (Brennecke etÂal. 2008; Khurana etÂal. 2011). The production of regulatory piRNAs requires the presence of at least one homologous TE insertion in a piRNA cluster and is amplified by the presence of additional TE copies elsewhere in the genome (Brennecke etÂal. 2008; Zanni etÂal. 2013). The enhancement of piRNA production by TE insertions outside of piRNA clusters is explained by the feed-forward biogenesis of piRNAs through transcriptional silencing of sense TE transcripts (i.e., ping-pong biogenesis; Brennecke etÂal. 2007; Gunawardane etÂal. 2007). piRNAs are maternally transmitted, such that piRNA production in the mother determines the strength of silencing in the offspring (Brennecke etÂal. 2008). Consistent with maternal transmission, repression of hybrid dysgenesis is genetically determined by a strict maternal effect (Ronsseray etÂal. 1993; Simmons etÂal. 2007; Belinco etÂal. 2009).

Empirical data regarding the quantitative relationship between TE copy numbers inside and outside of piRNA clusters and reductions in transposition rate are sparse for P-elements, and entirely lacking for other TE families. We therefore harnessed the extensive data on piRNA-mediated repression of dysgenic sterility (Ronsseray etÂal. 1991, 1996, 1998; Marin etÂal. 2000; Stuart etÂal. 2002; Simmons etÂal. 2007, 2012, 2014) (supplementary table S1 and fig. S1, Supplementary Material online). Based on these observations, we describe the strength of small-RNA-mediated silencing, R, conferred by maternal genotypes with at least one occupied small-RNA site as

$$R=1âe^{aâb{n}_{\mathrm{m}}},$$ (6)

where n_m is the total number of TE copies in the maternal genome, and a and b are constants. We fit equation (6) by nonlinear least squares to the data in supplementary table S1, Supplementary Material online, and obtained: $a=0.8Â0.5$ and $b=1.0Â0.4$ (estimates and 95% confidence intervals). R can vary from 0 (no repression) to 1 (complete repression).

Evolution

Each population is defined by the following parameters: population size (N), transposition rate $(Î)$, baseline ectopic recombination rate $(E_0)$, and the maximum possible fertility cost caused by dysgenic sterility (D). In the initial population, the sex of each individual is decided randomly, so that the expected sex ratio is 1:1. The range of parameter values we considered over our simulations is described in tableÂ3. Of the population, 5% harbors one TE insertion at a randomly chosen neutral site on chromosome 2. The remaining 95% of the population harbors no TE insertions.

Table 3.

Range of Parameter Values Explored for Diploid Population Size (N), Unrepressed Transposition Rate $(Î)$, Maximum Possible Fertility Cost Caused by Dysgenic Sterility (D), Baseline Ectopic Recombination Rate $(E_0)$

Parameter	Symbol	Values	Units
Diploid population size	N	$2Ã{10}^2,â2Ã{10}^3,â2Ã{10}^4$	Individuals
Transposition rate	Î	${10}^{â1},â{10}^{â2}$	Insertions per element per generation
Maximum dysgenic sterility	D	0, 0.1, 0.25, 0.5, 1	Proportional fitness
Baseline ectopic recombination rate	E0	0, ${10}^{â1},â{10}^{â2},â{10}^{â3},â{10}^{â4},â{10}^{â5}$	Proportional fitness

We simulated reproduction by randomly selecting one male and one female, each with probability proportional to their fitness (eq.Â2). After an individual parent is selected to reproduce, the number of new TE copies to transpose within its germline is drawn from a Poisson distribution with parameter u (eq.Â1). The new TE copies are distributed randomly among unoccupied sites and are only used to produce one specific offspring; if a parent produces multiple offspring, transposition is repeated independently for each offspring produced.

Haploid gametes are produced by meiosis, simulated by choosing one chromosome per pair at random. Crossing over occurs in females only, as is true for D. melanogaster (Morgan 1914). We assumed no crossover interference. Diploid progeny are formed by fusion of one gamete from each parent. Once N offspring are produced, the parents are discarded.

Materials and Methods

Statistical Analyses

All statistical analyses were conducted with R version 3.3 (R Core Team 2016). All graphs were produced in ggplot2 (Wickham 2009).

Data Availability

The software used to run all simulations was written in Perl and will be available at https://github.com/eskelleher/TE-invasion-simulations, last accessed October 25, 2018 at the time of publication.

Results

Transposition Rate Is a Key Determinant of Invasion Dynamics

We began by considering a conservative model, in which TEs impose only viability fitness effects by occupying functional sites in the host genome, and repression benefits the host by preventing the occurrence of deleterious TE insertions. Dysgenic sterility and ectopic recombination were not incorporated in the model $(D=0î¼,âE_0=0)$. We compared two baseline transposition rates $Î=0.1$ and $Î=0.01$, which encompass the range of most empirically estimated values for unregulated P-element transposition (Bingham etÂal. 1982; Eggleston etÂal. 1988; Robertson etÂal. 1988; Berg and Spradling 1991; Kimura and Kidwell 1994). We furthermore compared two different fitness models, one of which is matched to quantitative genetic estimates of the fitness costs of individual P-element insertions (Mackay etÂal. 1992; Lyman etÂal. 1996) (Ï_e), and a second in which these empirically estimated fitness effects are reduced 10-fold (Ï_r).

Simulations were started from populations of Nâ=â2,000 in which 5% of individuals harbor a single autosomal TE insertion at a neutral site. Starting the simulations with multiple individuals helped avoid the stochasticity of transposition and genetic drift, allowing us to focus on the deterministic phase of invasion and the associated evolution of repression. Populations were allowed to evolve for 2,000 generations.

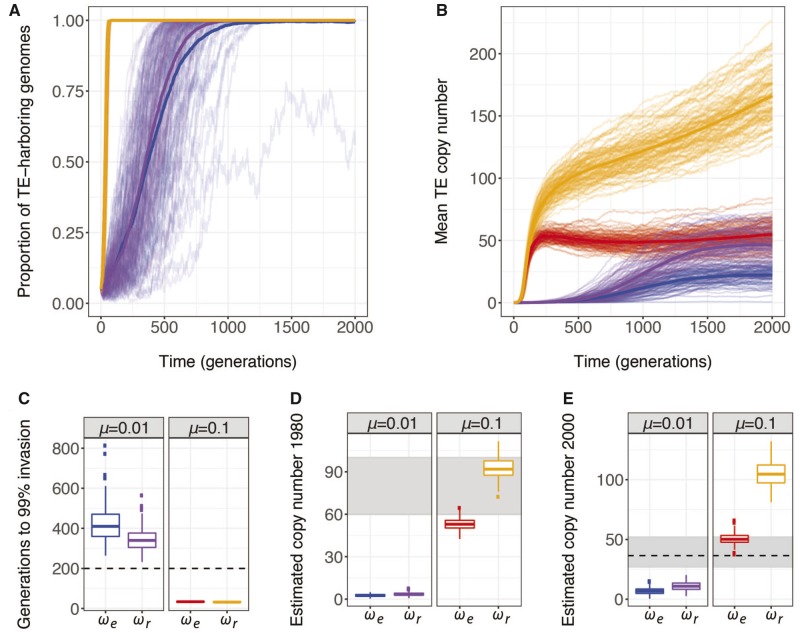
Transposition rate had a dramatic effect on invasion dynamics, with simulations assuming a higher transposition rate ($Î=0.1$) exhibiting complete invasion ($>99\%$ of individuals) in fewer than 35 generations on average, while those assuming a lower transposition rate of $Î=0.01$ had a comparable increase in invasion time of >10-fold (figs.Â1A and C). By contrast, the fitness model had almost no effect on invasion time at the higher transposition rate, and only a modest effect on invasion time at the lower transposition rate (figs.Â1A and C). Notably, the combination of higher fitness costs (Ï_e) and reduced transposition rate ($Î=0.01$) was associated with loss of the P-element in 29% of simulations. Presumably the reduced transposition rate is unable to sustain genomic TEs in the face of enhanced negative selection.

Fig. 1.

âTransposition rates, but not fitness, are key determinants of TE invasion. (A,B) Evolution of the (A) proportion of individuals with at least one genomic TE and (B) mean diploid TE copy number (n) over 2,000 generations in 100 replicate simulated populations are shown. (C) The number of generations required for the proportion of individuals with at least one genomic TE to increase from 33% to $>99\%$. (D,E) The mean diploid copy number in simulated populations after 300 generations (D) and 500 generations (E) after 1950 (i.e., first generation where $>33\%$ of individual genomes carry TEs). Gray boxes indicate empirical estimates of historic values (Bingham etÂal. 1982; Ronsseray etÂal. 1989; Srivastav and Kelleher 2017). For (A)â(E), the trajectory of invasion is compared for four different combinations of transposition rate and fitness effects: $Î=0.01$, Ï_e (blue), $Î=0.01$, Ï_r (purple),$Î=0.1$, Ï_e (red), and $Î=0.1$, Ï_e (orange). Note that the red and orange lines completely overlap in (A). All simulated populations (AâE) included Nâ=â2,000 individuals, who experienced neither dysgenic sterility nor ectopic recombination $(D=0î¼,âE_0=0)$.

In light of the difference in invasion dynamics between the two transposition rates, we wondered which set of simulations more closely matched the timescale of the historical P-element invasion. We focused on American populations (North and South), for which the historical record of the P-element invasion is particularly comprehensive (reviewed in Kelleher 2016). With the exception of a single strain collected in 1938, all wild-derived strains collected prior to 1950 lack genomic P-elements, indicating that the P-element was quite rare (Bingham etÂal. 1982; AnxolabÃhÃre etÂal. 1988). By contrast, $â33\%$ of collections from the 1950s (4/12 strains) and 1960s (4/13 strains) contain P-elements, and $â100\%$ of >200 strains collected after 1971 contain P-elements (AnxolabÃhÃre etÂal. 1988). Thus, in <20âyears, and possibly <10, P-elements went from intermediate frequency to complete fixation in the Americas, a rapid colonization event that was recapitulated in other geographic locations (AnxolabÃhÃre etÂal. 1988). This same rapid colonization has recently been documented in Drosophila simulans, with P-element invasion occurring in <10âyears (Hill etÂal. 2016).

To compare the observed colonization rate in D. melanogaster with our simulated data, we assumed that the first simulated generation where $>33\%$ of genomes contained P-elements in each population corresponded to the year 1950. We then determined how many additional generations were required for $>99\%$ of genomes to contain P-elements. Assuming ten generations per year for 20âyears, 99% colonized genomes should be achieved in <200 generations. Indeed, this occurred in 100% of simulations where $Î=0.1$, but 0% of simulations where $Î=0.01$ (all out of 100 runs; fig.Â1C), regardless of the fitness model. Thus, the timescale of the invasion in natural populations seems more consistent with higher transposition rates.

We further evaluated the effect of transposition rate and fitness costs on genomic TE copy numbers throughout our simulations. Unlike transposition rate, we observed that TE copy numbers reflect an interaction between transposition rate and fitness costs (fig.Â1B), with the highest copy numbers observed in simulations with the highest transposition rates and the lowest fitness costs. Interestingly, the combination of high transposition rate and high fitness costs ($Î=0.1$, Ï_e) exhibits similar copy numbers to the opposite combination ($Î=0.01$, Ï_r) later in the invasion process, but is associated with much higher copy numbers earlier in the invasion.

To more deeply interrogate the plausibility of our fitness models and transposition rates, we again considered the historical record in North America, this time with regards to P-element copy numbers. P-element containing strains collected in the late 1960s through the early 1980s were estimated by two different studies to contain 60â100 copies/diploid genome, based on Southern blotting (Bingham etÂal. 1982) and in situ hybridization of polytene chromosomes (Ronsseray etÂal. 1989). Based on next-generation sequencing data, Srivastav and Kelleher (2017) estimated somewhat lower values of â38â52 copies per diploid genome from a panel of isofemale lines collected in North Carolina in 2004. It should be noted that these values do not necessarily suggest a decrease in P-element copy number since the 1980s, because estimates from Southern blotting may be somewhat inflated by polymorphism, while estimates from deep-sequencing data are likely to be somewhat low, due to unannotated heterochromatic insertions (Zhang and Kelleher 2017), challenges in estimating copy number across structural variants (Srivastav and Kelleher 2017), and loss of deleterious copies during inbreeding.

We compared our simulated copy numbers with historical values from 1980 and 2004 by determining the mean diploid copy number in each simulated data set 300 and 500 generations after 33% of individual genomes contain P-elements (year 1950). For the higher transposition rate, 5% and 83% of simulated populations exhibit copy numbers in the range of historical estimates for 1980 under Ï_e and Ï_r, respectively (out of 100 runs; fig.Â1D, red, orange). By contrast, estimated copy numbers at lower transposition rates were an order of magnitude too low, regardless of the fitness model (fig.Â1D, blue, purple). Similarly, 100% of simulations at the lower transposition rate exhibit implausibly low copy numbers for the year 2000, while 61% of simulations with $Î=0.1$ and Ï_e are consistent with historic values (out of 100 runs, fig.Â1E). Interestingly, 100% of simulations under $Î=0.1$ and Ï_r exceed the range of historic values, suggesting that the reduced effect fitness model may allow implausibly high accumulation of TE copies (out of 100 runs, fig.Â1E).

Collectively, our observations suggest that transposition rate is a key determinant of invasion time and copy number and that simulations with higher transposition rates ($Î=0.1$) more closely recapitulate the historical invasion of P-elements in natural populations. By contrast, simulations with lower transposition rates of $Î=0.01$ exhibit unrealistically slow invasions with copy numbers that are more than an order of magnitude lower than historical values. While we also observed that fitness costs (Ï_e vs. Ï_r) affected invasion dynamics, these effects were more modest, with both fitness models being consistent with historic invasion times and at least partially consistent with historic copy numbers at the higher transposition rate (figs.Â1C and D). Notably, only simulations under the empirically estimated fitness model (Ï_e) in combination with the higher transposition rate ($Î=0.1$) are consistent with invasion times and copy numbers at both time points. For this reason, and because the fitness model is matched to quantitative genetic estimates of viability fitness costs for P-elements (Mackay etÂal. 1992; Lyman etÂal. 1996), we employ Ï_e and $Î=0.1$ for the remainder of our simulations.

Population Size Has Only Modest Effects on Invasion Dynamics but Enhances Positive Selection for Repression

Numerous previous studies of TE invasion dynamics employ a practice of parameter scaling, in which transposition rates and fitness costs are scaled inversely with population size (Dolgin and Charlesworth 2006, 2008; Lu and Clark 2010; Lee and Langley 2012; Groth and Blumenstiel 2017). This approach is motivated by the large number of generations required to reach copy number equilibrium when transposition rates are low, and is justified by the demonstration that the equilibrium copy number of a TE family under a negative epistasis fitness model can be kept constant through scaling (Dolgin and Charlesworth 2006, 2008). We were skeptical that a scaling approach would be necessary or appropriate for our study because 1) we are interested in invasion rather than equilibrium dynamics, 2) we employ a different fitness model than previous studies (Charlesworth B and Charlesworth D 1983; Dolgin and Charlesworth 2006), and 3) P-element transposition rates are considerably higher than those assumed by many previous studies (10^â4 in Dolgin and Charlesworth 2006, 2008; Lu and Clark 2010; Lee and Langley 2012; Groth and Blumenstiel 2017). We therefore evaluated the necessity for scaling by determining whether invasion dynamics (invasion time and copy number) are sensitive to population size in our model.

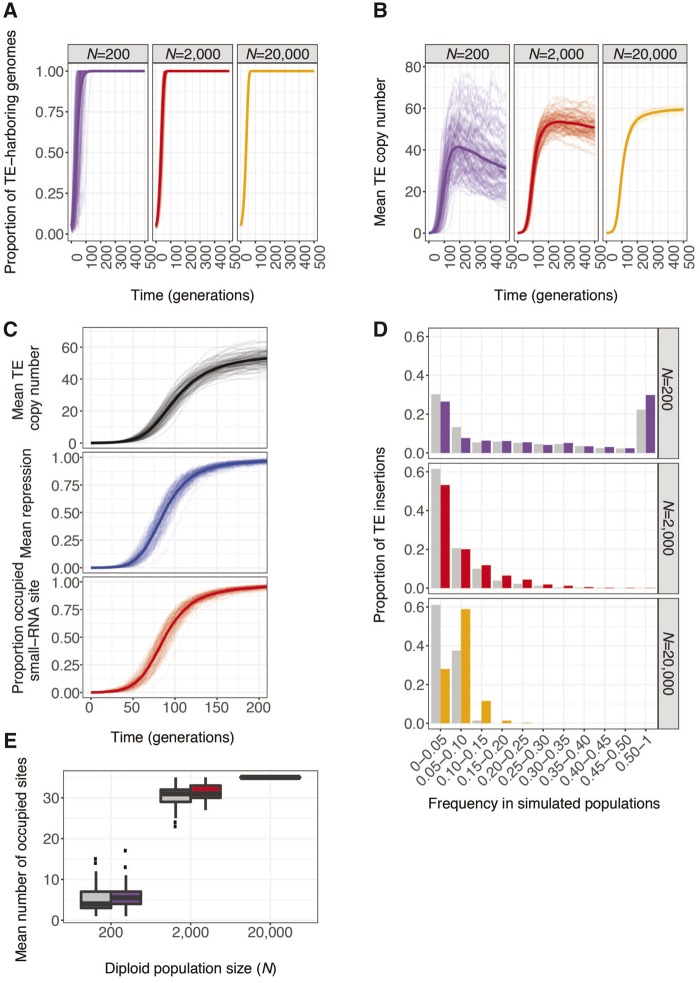
We observe that, in contrast to equilibrium TE copy number (Dolgin and Charlesworth 2006), invasion times are robust to different population sizes, as simulations of larger (Nâ=â20,000) and smaller (Nâ=â200) populations exhibit similar behavior in terms of invasion time (fig.Â2A and supplementary fig. S2, Supplementary Material online). Similarly, although mean copy numbers are slightly higher in larger populations (fig.Â1F), these higher copy numbers are more consistent with historic values (supplementary fig. S2, Supplementary Material online). Furthermore, the differences between Nâ=â2,000 and Nâ=â20,000 are so modest that realistic population sizes for D. melanogaster (e.g., $N_{\mathrm{e}}â2Ã{10}^6$; Garud etÂal. 2015) are not expected to differ dramatically in this respect. Indeed, the increased copy number we observe at higher population sizes further supports our use of the empirically estimated viability fitness effects (Ï_e), which are associated with lower copy numbers in simulated populations than arbitrarily reduced fitness effects (Ï_r; figs.Â1B, D, and E).

Fig. 2.

âPopulation size does not influence invasion, but enhances positive selection on repression. (A) Proportion of individuals with at least one genomic TE and (B) mean diploid TE copy number (n), over 500 generations in 100 replicate simulated populations of Nâ=â200 and Nâ=â2,000 individuals, and 10 replicate simulated populations of Nâ=â20,000 individuals are compared. (C) Evolution of mean genomic TE copy number (black, top), the mean maternal repression (R, blue, middle), and proportion of the population with $â1$ occupied small-RNA site (red, bottom) over 200 generations in 100 replicate simulated populations of Nâ=â2,000 individuals. Thick lines represent the average responses across all replicate populations. (D) The site frequency spectra of occupied small-RNA-producing sites (colored), which enact maternal repression of transposition, and pseudo-small-RNA-producing sites (gray) which do not repress transposition. The spectra were calculated by pooling the data from all replicate simulated populations. Site frequency bins include sites whose frequencies are higher than the lower bound, and less than or equal to the upper bound. (E) The average number of occupied small-RNA (colored) and pseudo-small-RNA sites (gray) in each replicate simulated population. A site is considered occupied if it carries a TE insertion in at least one individual in a population. Results shown in (D) and (E) are after 500 generations of simulated evolution. Individuals in all simulations had a baseline transposition rate of $Î=0.1$, an empirically estimated fitness model (Ï_e), and experienced neither dysgenic sterility nor ectopic recombination $(D=0î¼,âE_0=0)$.

We further considered how population size is related to selection for repression in simulated populations. In general, selection is more effective in larger populations, due to the reduced impact of genetic drift on segregating alleles (Kimura 1968). In our simulations, TE insertions in small-RNA sites are potential targets of positive selection based on their ability to establish maternal repression. Consistent with the evolution of repression, we observe that increased TE copy numbers are closely accompanied by increased strength of maternal repression, and an increasing frequency of individuals with P-element insertions in small-RNA-producing sites (fig.Â2C). We therefore examined the site frequency spectrum of TE insertions in small-RNA producing sites after 500 generations of simulated evolution. We compared these sites with control pseudo-small-RNA sites, neutral sites that do not produce small RNAs when occupied by TEs but otherwise are matched to small-RNA sites in their genomic locations and fitness effects (see Model). Positive selection will increase the frequency of occupied small-RNA sites as compared with occupied pseudo-small-RNA sites (Fay and Wu 2000; Nielsen 2005).

Consistent with positive selection for repression, the site-frequency spectrum of occupied small-RNA-producing sites is significantly different than that of pseudo-small-RNA sites (KolmogorovâSmirnov test, Nâ=â200: D_KS = 0.10, Pâ=â0.01; Nâ=â2,000: D_KS = 0.09, $P=1.52Ã{10}^{â5}$; Nâ=â20,000: D_KS = 0.34, $P<{10}^{â15}$), with occupied small-RNA sites segregating at higher frequency than their neutral counterparts across a range of population sizes (fig.Â2D). Notably, positive selection is also observed in populations of Nâ=â2,000 under the reduced fitness model (supplementary fig. S3, Supplementary Material online), suggesting that these observations are also somewhat robust to the magnitude of deleterious fitness effects associated with TE insertions.

One potential concern with our inference of positive selection is that linkage disequilibrium between small-RNA sites and functional sites increases modestly with decreasing population size (supplementary fig. S4, Supplementary Material online), which could enhance selection for repression in smaller simulated populations by maintaining relationships between repressor alleles and the genomic sites they have protected from deleterious insertions (Charlesworth and Langley 1986). If this type of artifact were responsible for our observation of positive selection, then the signature of selection would be stronger in smaller simulated populations as compared with larger ones. We observe the opposite, that the difference in the site-frequency spectra of selected and neutral sites becomes more pronounced in larger populations, as predicted by increased efficacy of natural selection acting on similarly beneficial mutations. These observations further demonstrate that our approach of using unscaled, biologically relevant parameters makes our inferences of positive selection conservative, as the impact of selection would be stronger in the larger natural population sizes of D. melanogaster (e.g., $N_{\mathrm{e}}â2Ã{10}^6$; Garud etÂal. 2015).

Additional evidence of positive selection is provided by the number of segregating (i.e., occupied in at least one individual) small-RNA sites, as compared with pseudo-small-RNA sites, in each simulated population at generation 500. In populations of Nâ=â200 and Nâ=â2,000, there were a greater number of segregating occupied small-RNA sites than pseudo-small-RNA sites (Nâ=â200: small RNA $\stackrel{Â}{S}=5.86$, pseudo-small RNA $\stackrel{Â}{S}=4.83$, permutation Pâ=â0.0067; Nâ=â2,000: small RNA $\stackrel{Â}{S}=31.26$, pseudo-small RNA $\stackrel{Â}{S}=30.33$, permutation Pâ=â0.0036; fig.Â2E). Because these sites occur in equal numbers in the genome, this indicates that small-RNA-producing insertions are retained by positive selection. The number of segregating small-RNA and pseudo-small-RNA sites could not be compared for the largest population size (Nâ=â20,000), because all sites of both classes were occupied in every replicate population (fig.Â2E).

Moderate Dysgenic Sterility Enhances Positive Selection for Repression

After identifying appropriate transposition rates and viability fitness effects, and demonstrating that our invasion model is robust to differences in population size, we wished to evaluate the potential for dysgenic sterility to enhance positive selection on repressor alleles. In Drosophila, dysgenic sterility occurs in the germline of F1 offspring from paternal genotypes containing transpositionally active elements and maternal genotypes that do not produce sufficient regulatory piRNAs (Blumenstiel and Hartl 2005; Josefsson etÂal. 2006; Brennecke etÂal. 2008; Chambeyron etÂal. 2008; Rozhkov etÂal. 2010). We therefore modeled fitness costs of dysgenic sterility as dependent on an individualâs TE copy number and the strength of maternal small-RNA silencing. Although our copy-number-dependent function for dysgenic sterility is based on empirical data (Bingham etÂal. 1982), it is difficult to identify a realistic magnitude for the fertility cost, because the penetrance of the sterility phenotype depends greatly on temperature (Kidwell etÂal. 1977; Engels and Preston 1979). We therefore considered a range of values for the maximum reduction in fertility that occurs due to dysgenic sterility (Dâ=â0, 0.1, 0.25, 0.5, and 1).

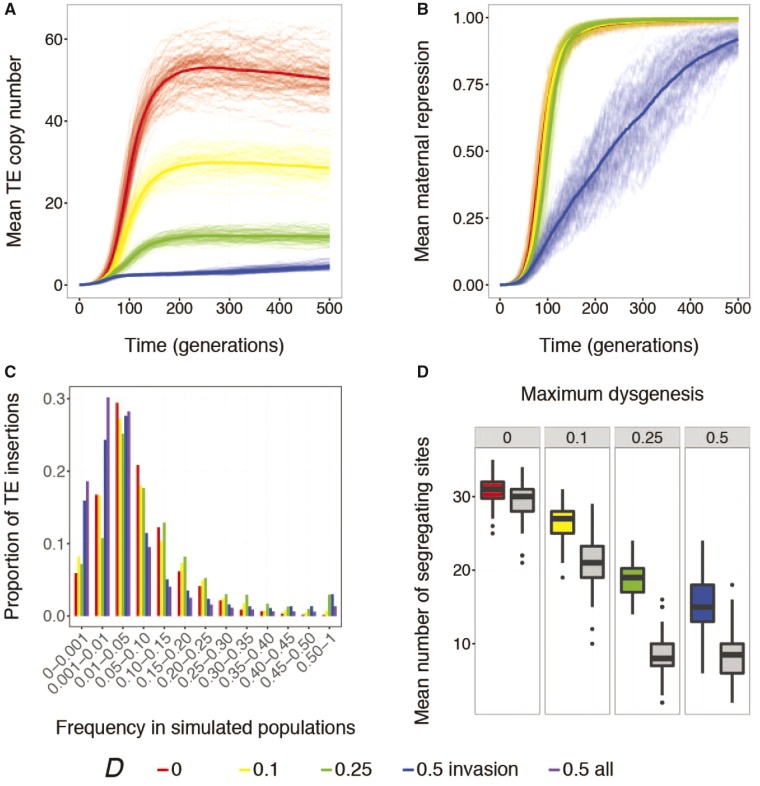
We observed that high rates of dysgenic sterility greatly enhance the fitness costs of TEs, thereby prohibiting invasion into simulated populations. The TE failed to invade completely (i.e., the TE did not occur in $â99\%$ of individual genomes at generation 500) in 100% of 377 simulated populations where Dâ=â1, and 74% of 381 simulated populations where Dâ=â0.5 (supplementary fig. S5, Supplementary Material online). Invasions were successful in the remaining 26% of simulations where Dâ=â0.5, but copy numbers remained extremely low due to negative selection. By contrast, 100% of simulations with lower rates of dysgenic sterility (Dâ=â0.1 or 0.25) exhibited successful invasion (fig.Â3A).

Fig. 3.

âPositive selection on repressor alleles is enhanced by increasing costs of hybrid dysgenesis. Evolution of (A) mean diploid TE copy number (n) and (B) maternal repression (R) over 500 generations of simulated evolution. The thick line represents the average response across all replicate populations. (C) The site frequency spectra of occupied small-RNA-producing sites after 500 generations of simulated evolution. The spectra were calculated by pooling the data from all replicate simulated populations. Site frequency bins include sites whose frequencies are higher than the lower bound, and less than or equal to the upper bound. (D) The average number of occupied small-RNA (colored) and pseudo-small-RNA (gray) sites in each replicate simulated population after 500 generations. A site is considered occupied if it carries a TE insertion in at least one individual in a population. Population sizes were Nâ=â2,000 for all simulations, and individuals had a baseline transposition rate of $Î=0.1$, an empirically estimated fitness model (Ï_e), and experienced no ectopic recombination $(E_0=0)$. Colors indicate simulations with different values for maximum hybrid dysgenesis (D). For Dâ=â0.5, blue indicates only simulated populations that exhibited successful invasion while purple indicates all simulated populations.

Increased negative selection against TEs has potentially opposing effects on the evolution of small-RNA-mediated repression. Although the additional fitness costs imposed by dysgenic sterility could enhance positive selection on occupied small-RNA sites, lower TE copy numbers would also correspond to a lower rate at which repressor alleles are produced by transposition, delaying the evolution of repression. With moderate costs of dysgenic sterility (Dâ<â0.5), we detect these opposing effects. Although repression evolves within $â200$ generations of invasion, repressive individuals emerge later in the invasion when values of D are higher (fig.Â3B and supplementary fig. S6, Supplementary Material online). Nevertheless, higher values of D are also associated with more high-frequency occupied small-RNA sites after 500 generations of simulated evolution, indicative of enhanced positive selection for repression (fig.Â3C). Enhanced positive selection is also evident from the increased number of segregating small-RNA sites, as compared with pseudo-small-RNA sites, in simulated populations (fig.Â3D;Dâ=â0: $t_{198}=3.76$, Pâ=â0.0022; Dâ=â0.1: $t_{198}=12.09,âP<{10}^{â15}$; Dâ=â0.25: $t_{198}=26.71,âP<{10}^{â15}$).

When the costs of dysgenic sterility were high (Dâ=â0.5), we observed a different selective regime, in which TE proliferation was limited by purifying selection to such an extent that positive selection for repression was weakened. In these simulations, maternal repression increased in a slower, more linear fashion (fig.Â3B, blue), and occupied small-RNA sites were not segregating at higher frequency after 500 generations of simulated evolution when compared with Dâ=â0.25 (fig.Â3C, blue vs. green). Furthermore, if we consider the full set of simulations for Dâ=â0.5 (both successful and failed invasions), high frequency occupied small-RNA sites ($â50\%$ of chromosomes) are even less common, suggesting that the requirement for successful invasion within 500 generations results in an ascertainment bias toward simulated populations with stronger repression (fig.Â3C, purple). In addition to a weaker footprint of positive selection on their site frequency spectra, we also find less evidence for selective retention of occupied small-RNA sites in simulated populations when Dâ=â0.5. While the mean number of segregating pseudo-small-RNA sites in simulated populations at generation 500 does not differ between Dâ=â0.5 and Dâ=â0.25 ($t_{198}=0.14$, Pâ=â0.89), larger numbers of segregating small-RNA sites are observed when Dâ=â0.25 $(\stackrel{Â}{S}=18.67)$ than when Dâ=â0.5 ($\stackrel{Â}{S}=15.63,ât_{198}=7.09,âP=2.35Ã{10}^{â11}$).

Ectopic Recombination Enhances Positive Selection for Repression

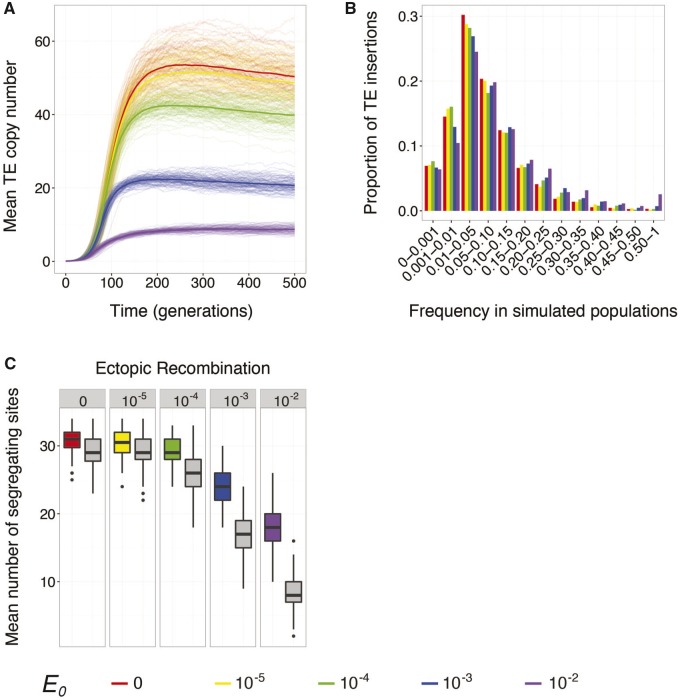
We lastly considered the impact of fitness costs imposed by ectopic recombination. In our model, the probability of an ectopic recombination event in an individualâs germline increases faster than linearly with TE copy number (eq.Â5), effectively producing negative epistasis between TE insertions. Thus, this fitness model is most similar to the model employed by previous forward simulations of the evolution of host repression (Lu and Clark 2010; Lee and Langley 2012). However, in our simulations small-RNA silencing repressed not only transposition but also the fitness costs associated with ectopic recombination. For simplicity, individuals did not experience hybrid dysgenesis in these simulations (Dâ=â0).

While invasion times are largely unchanged, higher baseline ectopic recombination rates $(E_0)$ were associated with lower TE copy numbers throughout the simulation (fig.Â4A), as expected from the higher fitness cost for each TE. Similar to hybrid dysgenesis, fitness costs imposed by ectopic recombination were associated with enhanced positive selection on occupied small-RNA sites. The site frequency spectra for occupied small-RNA sites at the end of the 500 generations of simulated evolution included a greater proportion of high-frequency variants, with 45% of 100 populations exhibiting a high-frequency $(â50\%)$ occupied small-RNA site at the highest baseline ectopic recombination rate we considered ($E_0=0.01$, fig.Â4B, purple). Similarly, the difference between the average number of occupied small-RNA sites and pseudo-small-RNA sites was more pronounced at higher E₀ values, indicating that selection increasingly retained occupied small-RNA sites (fig.Â4C).

Fig. 4.

âPositive selection on repressor alleles is enhanced by increasing costs of ectopic recombination. (A) Evolution of mean diploid TE copy number (n) over 500 generations of simulated evolution. The thick line represents the average response across all replicate simulated populations. (BâC) The site frequency spectra of occupied small-RNA-producing sites (B) and the average number of occupied small-RNA and pseudo-small-RNA sites (C) after 500 generations of simulated evolution. Site frequency spectra (B) were calculated by pooling the data from all replicate simulated populations. Site frequency bins include sites whose frequencies are higher than the lower bound, and less than or equal to the upper bound. A site is considered occupied (C) if it carries a TE insertion in at least one individual in a population. Population sizes were Nâ=â2,000 for all simulations, and individuals had a baseline transposition rate of $Î=0.1$, an empirically estimated fitness model (Ï_e), and experienced no dysgenic sterility (Dâ=â0). Colors compare simulations with different values of the baseline ectopic recombination rate $(E_0)$.

Positive Selection on Repressor Alleles Is Weaker When Small-RNA Sites Are Abundant in the Host Genome

Although occupied small-RNA-producing sites were targets of positive selection in many of our simulations, a given population was generally segregating for multiple such repressor alleles after 500 generations (figs.Â2C, 3D, and 4C). These observations suggest that the evolution of small-RNA-mediated TE silencing in simulated populations proceeds through a soft-sweep-like process, in which multiple small-RNA-producing TE insertions in different genomic sites increase in frequency concurrently by positive selection. The key determinant of soft-sweep dynamics is the rate at which adaptive mutations arise within populations and individual genomes (i.e., the degree to which adaptation is mutation-limited; Pennings and Hermisson 2006a, 2006b; Pritchard etÂal. 2010). When adaptive mutations occur frequently, because population sizes are large, or in the case of small-RNA-mediated TE repression, many loci (i.e., small-RNA sites) affect a phenotype, multiple beneficial mutations can co-occur in the same population, allowing for soft-sweeps.

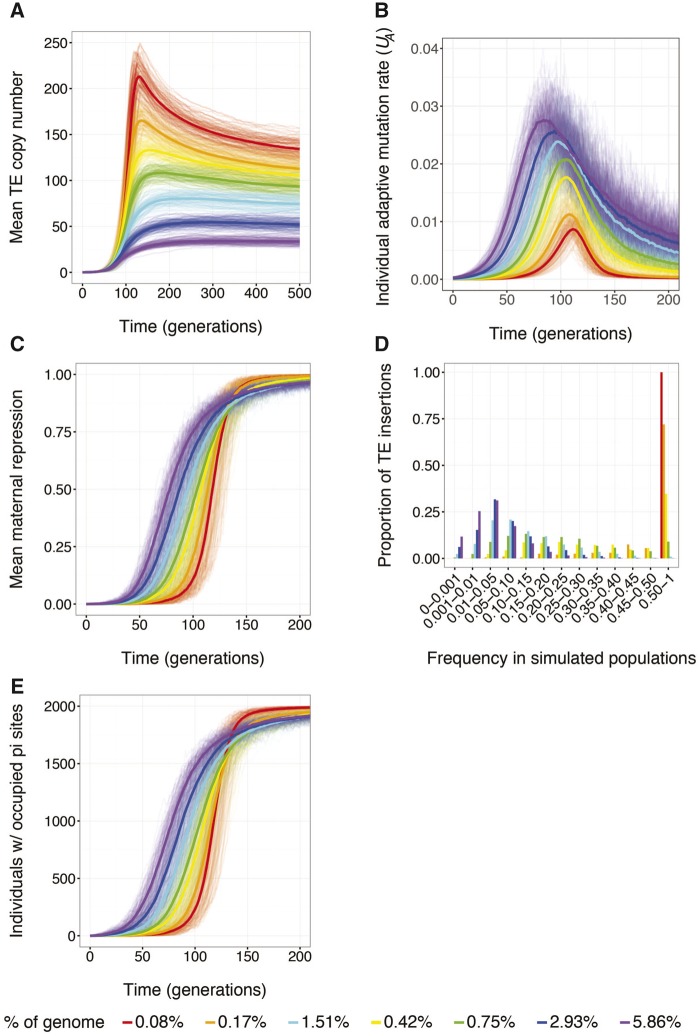
To better understand the potential role of soft-sweeps in the evolution of small-RNA silencing, we considered invasion into populations where the number of small-RNA sites in the genome differed (fig.Â5A), corresponding to differences in the individual adaptive mutation rate (U_A). By estimating U_A as the product of individual transposition rate U and the proportion of small sites in the genome, we confirmed that U_A is higher throughout the simulation when small-RNA sites are common in the host genome, as compared with when small-RNA sites are rare (fig.Â5B). Regardless of the number of small-RNA sites, repression evolves within 200 generations of TE invasion, indicating that the individual adaptive mutation rate does not effect the timescale on which small-RNA-mediated silencing evolves (fig.Â5C). However, differences in the individual adaptive mutation rate were associated with different trajectories for the evolution of maternal repression within simulated populations. When small-RNA sites are common, repressive individuals arise earlier in the invasion (<50 generations) but increase in abundance at a slower exponential rate. In contrast, when there are few small-RNA-producing sites, repression remains rare for much longer but spreads much more rapidly.

Fig. 5.

âThe abundance of small-RNA sites is related to the strength of positive selection for repression. (A) Evolution of the mean diploid TE copy number (n) over 500 generations in simulated populations. (B,C,E) Evolution of the mean individual adaptive mutation rate (U_A, insertions into small-RNA sites per genome) (B), the mean maternal repression (R) (C), and the cumulative frequency of individuals with at least one occupied small-RNA site (E), over 200 generations in replicate simulated populations. The thick line represents the average response across 100 replicate populations. (D) The site frequency spectra of occupied small-RNA-producing sites after 500 generations of simulated evolution. Site frequency bins include sites whose frequencies are higher than the lower bound, and less than or equal to the upper bound. The site frequency spectra were calculated by pooling the data from all 100 replicate simulated populations. All simulations included Nâ=â2,000 individuals, who had a baseline transposition rate of $Î=0.1$, an empirically estimated fitness model (Ï_e), and who experienced neither dysgenic sterility nor ectopic recombination $(D=0î¼,âE_0=0)$. Colors indicate simulations that involved genomes with different fractions of small-RNA-producing sites.

The more rapid increase in repression when small-RNA sites are rare suggests enhanced positive selection. Although small-RNA sites segregate at higher frequency when they are rare (fig.Â5D), the inference of stronger positive selection is confounded by the fact that occupied small-RNA sites arise less frequently, increasing the probability that the first occupied small-RNA site reaches fixation before a new one arises. We therefore considered the cumulative frequency of individuals harboring at least one insertion in a small-RNA-producing site over the course of simulated evolution (fig.Â5E), in order to examine the increase in frequency of the repressor allele class as a whole. The cumulative frequency of individual genomes with at least one repressor allele increases more rapidly when small-RNA sites are rare, suggesting stronger positive selection in simulated populations. Furthermore, simulations with fewer genomic small-RNA sites were associated with the accumulation of a greater number of TE copies, suggesting that mutation-limitation enhances selection for repression because of an increased deleterious mutation rate resulting from transposition. Indeed, the accumulation of TE copies in genomes with fewer small-RNA sites is associated with decreased mean population fitness and increased variance in fitness (supplementary fig. S7, Supplementary Material online).

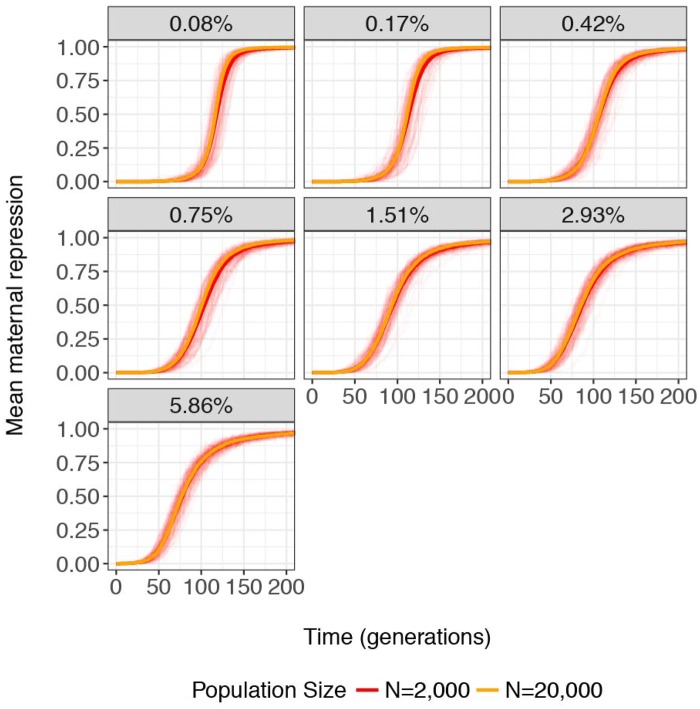
Population size is also an important determinant of soft-sweep dynamics, because larger populations contain a larger number of individual genomes within which an adaptive mutation can occur (Pennings and Hermisson 2006b). We therefore considered how differences in the degree of mutation-limitation between larger (Nâ=â20,000) and smaller (Nâ=â2, 000) populations could impact the evolution of repression. Puzzlingly, larger populations do not exhibit stronger repression earlier in the invasion process (fig.Â6 and supplementary fig. S8, Supplementary Material online) as would be predicted if they are less mutation-limited. However, it must be considered that the strength of selection for repression of an invading TE is temporally dynamic, and increases over time as TE copies accumulate. Early in the invasion process, repressor alleles will likely be neutral because deleterious TE insertions are rare. Therefore, by the time repressor alleles enjoy a selective advantage, they may be present at similar frequencies in populations of differing size, but selection will be more effective in larger populations. This likely explains why repression increases at equivalent rates in large and small simulated populations early in the invasion process but exhibits a more accelerated increase in the later generations of larger populations.

Fig. 6.

âLarger populations do not exhibit repression earlier in invasion. The abundance of small-RNA sites (genomic percentage) is related to the evolution of mean maternal repression (R) over 200 generations in replicate simulated populations of Nâ=â2,000 (red) and Nâ=â20,000 (orange).The thick line represents the average response across 100 replicate populations for Nâ=â2,000, 30 replicate populations for Nâ=â20,000 and a small-RNA site percentage of 2.93%, and 10 replicate populations for all other small-RNA site percentages.

Discussion

We harnessed the deep body of literature on P-element transposition and fitness effects (reviewed in Kelleher 2016), as well as piRNA-mediated silencing of TEs (reviewed in Senti and Brennecke 2010), in D. melanogaster to construct a forward simulation model of TE invasion and the evolution of host repression that is grounded in known biology. The validity of our model is supported by the degree to which our findings mirror empirical observations of P-element invasion in D. melanogaster. P-elements transitioned from rare to ubiquitous in natural populations in <20âyears (AnxolabÃhÃre etÂal. 1988), a rapid timescale that is matched by our simulated populations, in which invasion occurred in <100 generations (fig.Â1A). Similarly, average P-element copy numbers in individual genomes in our simulated populations were in the range $â5â60$, which matches estimates from wild-derived genomes (Ronsseray etÂal. 1989; Srivastav and Kelleher 2017; figs.Â1B, D, and E). Finally, repression in many natural populations evolved in <30âyears (Kidwell 1983), which is echoed by our observation that the vast majority of populations evolve repression in <200 generations (figs.Â2C and 3B).

Although our model is, by design, informed by the specific biology of P-elements in D. melanogaster, our findings have general implications for TE invasion and the evolution of TE repression. Horizontal transfer of TEs and post-invasion TE proliferation are ubiquitous across the tree of life (reviewed in Schaack etÂal. 2010). Similarly, small-RNA-mediated silencing is a ubiquitous mechanism for TE control, employed by both prokaryotes and eukaryotes (reviewed in Blumenstiel 2011). Our results therefore provide fundamental insights about the trajectory of TE invasion into new genomes, and the regulatory response of genomes to new invaders.

Weak Selection for Repression of Transposition?

Charlesworth and Langley (1986) suggested that selection for transpositional repression was likely to be weak in sexually reproducing organisms, because recombination would rapidly separate repressor alleles from chromosomes that they have protected from incurring deleterious mutations. Furthermore, they proposed that the adaptive evolution of transpositional repression relied on a sufficiently high frequency of dominant deleterious insertions and a sufficiently large effective population size. Consistent with this prediction, previous simulations of small-RNA-mediated retrotransposon silencing, which assumed dominant deleterious effects of new insertions and large effective population sizes, observed selection for repressor alleles (Lu and Clark 2010). It is counterintuitive, therefore, that we also observed positive selection for repressor alleles in relatively small populations of Nâ=â2,000 individuals, with entirely recessive effects of TE insertions on viability fitness.

The apparent contradiction between our findings and the predictions of Charlesworth and Langley (1986) is at least partially explained by differences in the transposition rates we considered. The empirically estimated transposition rate for an unmarked P-element of 0.1 (new insertions/element/genome) (Eggleston etÂal. 1988) is multiple orders of magnitude higher than âtypicalâ estimates of transposition rate in Drosophila ($â{10}^{â4}â{10}^{â5}$; Nuzhdin 1999). The high transposition rates of P-elements may be more realistic; however, because lower transposition rate estimates were obtained from TE families we now understand to be regulated (i.e., have evolved a lower transposition rate) by the piRNA pathway (Nuzhdin 1999; Brennecke etÂal. 2007). Higher transposition rates cause greater fitness benefits of repression, because they increase the likelihood of a deleterious insertion and therefore the relative advantage of an uninserted chromosome.

The fitness model that we employed in this study, which was based on the transpositional bias of P-elements into functional sites (Bellen etÂal. 2004, 2011; Spradling etÂal. 2011), and the estimated fitness effects of individual P-element insertions (Cooley etÂal. 1988; Mackay etÂal. 1992), likely also contributes to the strength of selection we observe. Although they act recessively, the empirically estimated fitness effects of P-element insertions are quite deleterious, with an average fitness cost of 12.2%, and 3.7% of sites acting as recessive lethals (Cooley etÂal. 1988; Mackay etÂal. 1992; Lyman etÂal. 1996). Similar to high transposition rates, these dramatic fitness consequences enhance the benefits of repressing transposition. However, we note that our inference of positive selection is at least moderately robust to the magnitude of these fitness effects, because elevated polymorphic frequencies of occupied small-RNA sites were observed even in the reduced fitness costs model (Ï_r; supplemental material S3, Supplementary Material online). TEs exhibit a diversity of preferences for particular insertion sites, and the degree to which these preferences influence selection for transpositional repression remains unknown.

Repression of Dysgenic Sterility and Ectopic Recombination Enhances Adaptive Evolution of small-RNA-Mediated TE Silencing

In addition to deleterious insertions, we examined whether the fitness effects of dysgenic sterility and ectopic recombination can enhance selection for repression in simulated populations (figs.Â3C and 5B). It is notable that in our model, both of these fitness effects are dominant and epistatic, reflecting the cumulative effects of multiple TE insertions across the genome. This differs from the viability fitness effects that result from the disrupted function of particular host genes, which are recessive and multiplicative. Furthermore, while our fitness models for dysgenic sterility and ectopic recombination mirror the negative epistasis model assumed by previous simulation models of TE dynamics (Dolgin and Charlesworth 2006, 2008; Lu and Clark 2010), in our model these costs are directly alleviated by small-RNA mediated silencing, as opposed to being reduced only indirectly by repression as a consequence of reduced TE copy number. These direct effects are motivated by the known biology: Small-RNA-mediated silencing directly suppresses hybrid dysgenesis by reducing DNA damage associated with transposition (Khurana etÂal. 2011). Similarly, small-RNA-mediated silencing may directly repress ectopic recombination by inducing heterochromatin formation at TE loci.

We observed that dysgenic sterility in particular strengthens selection for host repression in simulated populations. Our results differ from those of Lee and Langley (2012), who previously considered selection on small-RNA-independent repressors of dysgenic sterility. They observed that strong selection on the repressor allele was too ephemeral to produce significant changes in its population frequency, owing to the rapid loss of nonrepressive maternal genotypes from the population. However, they also assumed that the presence of P-elements in the maternal genome was sufficient to establish small-RNA silencing, rather than explicitly modeling the production of regulatory small RNAs from insertions at particular sites as we do here. Our observations therefore suggest that dysgenic sterility can be an important agent of selection for TE regulation, at least during TE invasion. Dysgenic sterility may further be a common cost of TEs that selects for repression in their hosts. In Drosophila, multiple historic TE invasions are associated with dysgenic sterility syndromes (Bingham etÂal. 1982; Bucheton etÂal. 1984; Blackman etÂal. 1987; Evgenâev et al. 1997; Hill etÂal. 2016), and at least three of these syndromes have been attributed to the absence of maternally deposited piRNAs (Blumenstiel and Hartl 2005; Brennecke etÂal. 2008; Chambeyron etÂal. 2008; Rozhkov etÂal. 2010). More broadly, mutations that impact TE regulation are associated with fertility defects in diverse eukaryotes (reviewed in CastaÃeda etÂal. 2011; Mani and Juliano 2013).

Our study also represents the first evaluation of whether repression of ectopic recombination could enhance selection for small-RNA-mediated silencing. Similar to dysgenic sterility, we observed enhanced positive selection on small-RNA-mediated repressors at higher ectopic recombination rates (figs.Â4B and C). Because TE copy numbers remained relatively low in the simulations we presented here (generally <60 copies), positive selection could be much stronger in large, repeat-rich genomes, where individual elements can be represented by thousands of copies (e.g., Naito etÂal. 2006). Suppression of ectopic recombination may therefore represent a major benefit of small-RNA-mediated repressor alleles. However, in contrast to the benefits of repressing transposition and potentially ectopic recombination, heterochromatin formation at TE loci (i.e., transcriptional silencing) can also have a deleterious effect if it interferes with host gene expression. Such deleterious effects have been observed in both Arabidopsis (Hollister and Gaut 2009) and Drosophila (Lee 2015; Lee and Karpen 2017). Exploring trade-offs between the costs and benefits of transcriptional repression, and how such trade-offs influence transcriptional versus posttranscriptional regulation of TEs, would make an interesting direction of future study.

The Abundance of Small-RNA-Producing Sites Is a Major Determinant of Postinvasion Dynamics

In the D. melanogaster genome we used as a model for our simulations, the small RNAs that regulated TEs are thought to be encoded by >100 independent loci, comprising $â3\%$ of genomic sites (Brennecke etÂal. 2007). Small-RNA-mediated silencing is therefore a polygenic trait encoded by a large mutational target, a property that is shared with other taxa. Although the power to identify loci that give rise to TE-regulating small RNAs can be limited by the quality of the genome assembly as well as its repeat content, large numbers of repeat-rich small-RNA-producing sites are also implicated in TE regulation in mouse (Aravin etÂal. 2006), Caenorhabditis (Ni etÂal. 2014), and even Arabidopsis (reviewed in Lisch and Bennetzen 2011).

Polygenic traits that are determined by many loci are predicted to undergo adaptation via soft selective sweeps (Pritchard etÂal. 2010), in which multiple beneficial alleles increase in frequency but do not reach fixation (Pennings and Hermisson 2006a, 2006b). Throughout our simulations, we observed exactly these soft-sweeps, in which beneficial insertions in small-RNA-producing sites segregate at higher frequency than their neutral counterparts, but rarely reach fixation (figs.Â2D, 3C, and 4B). Our results are consistent with multiple independent P-element insertions into piRNA clusters that have been reported in natural populations of D. melanogaster (Ronsseray etÂal. 1996; Marin etÂal. 2000; Stuart etÂal. 2002; Khurana etÂal. 2011, reviewed in Kelleher 2016). We furthermore discovered that the larger the number of small-RNA sites in the genome, the weaker selection for repression becomes, because the mutational load of deleterious insertions that select for repression is decreased (fig.Â5A and supplementary fig. S7, Supplementary Material online). To the best of our knowledge, this unexpected relationship between mutational target size and positive selection is unique to the evolution of TE repression, because the enhanced benefits of repression when small-RNA sites are rare reflect accumulating TE copy numbers.

Why are small-RNA-producing sites so common in host genomes? An appealing adaptive explanation is that the large mutation target facilitates the establishment of silencing when new TE families invade (Kelleher 2016). However, our findings do not support this model, as repression evolved within $â200$ generations regardless of the number of small-RNA sites in the theoretical genome (fig.Â5C). Rather, we observed that the mutational target size has a dramatic impact on the maximum copy number the TE achieves after invasion, with genomes containing fewer small-RNA sites accumulating many more TE copies (fig.Â5A). This accumulation of TE copies can be attributed to longer individual waiting times for the occurrence of the first repressor allele, during which time TEs enjoy unrestricted transposition (figs.Â5C and E).

The magnitude of interspecific variation in the proportion of the genome that corresponds to small-RNA-producing sites remains largely unknown. In part this reflects the challenge of annotating such sites, which lack diagnostic primary sequence features, and whose transcripts are rapidly processed into short sequences that align to multiple genomic locations (Brennecke etÂal. 2007; Rosenkranz and Zischler 2012). Nevertheless, our observations suggest an unexpected benefit to having more small-RNA sites, namely, that the larger mutational target buffers genomes against postinvasion proliferation. They further provide a potential explanation for rapid, TE-mediated expansions in genome size, which have been observed in certain vertebrate and plant lineages (Sun and Mueller 2014; Lee and Kim 2014). If the relative fraction of the genome that corresponds to small-RNA-producing sites decreases when genome size expands, a type of snowballing could occur, in which large genomes experience increasingly dramatic TE proliferations and corresponding decreases in the relative abundance of small-RNA-producing sites.